后台开发学习笔记（三、链表）

由于上一节最后的桶排序和基数排序都需要用到链表，所以这一节先补补链表，栈。队列。哈希表的知识。

3.1 链表

3.1.1 单链表

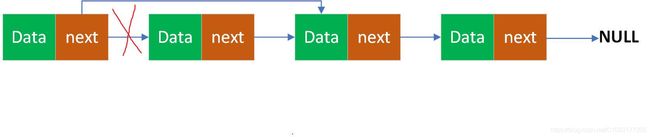
链表感觉都没什么好说的，是嵌入式使用的比较多的一种数据结构，但是也要基本介绍介绍，下面是单向链表的结构：参考《漫画算法》

链表是一种在内存中非连续，非顺序的数据结构，由若干节点所组成。单链表看到图发现由两部分组成，一部分是存放数据的变量data，一部分是存放指向下一个节点的指针next。

typedef struct single_link
{
	int data;    					//数据区域
	struct single_link *next;		//指向下一个节点
}_single_link_T;

为了方便操作，我们都会把链表的第一个节点称为头节点，头节点的data值一般没意义，不过通常习惯保存这个链表的长度，最后一个节点称为尾节点，尾节点的指针指向NULL，每次遍历的时候都是判断next指针是否为NULL来判断节点是不是结束。
从图也可以看到，链表是通过next指针指向下一个，下一个的next又指向下一个。

3.1.2 双链表

单链表中有一个不好的地方就是查找上一个的时候，不方便，所以这时候引入了双向链表，双向链表的意思就是在链表节点中又添加了一个指向上一个的指针，名字为prev指针。双链表的结构：

由图可以看出两个指针next、prev分别指向下一个和上一个

//双链表结构体
typedef struct double_link
{
	int data;   	 				//数据区域
	struct double_link *prev;		//指向上一个节点
	struct double_link *next;		//指向下一个节点
}_double_link_T;

使用一个数据结构，简单的方法就是增、删、改、查

3.1.3 链表的基本操作

1. 增
   链表的增，有两种方式，一个是尾插法，一种是头插法。
   单链表的增加操作，看图：
   尾插法：
   
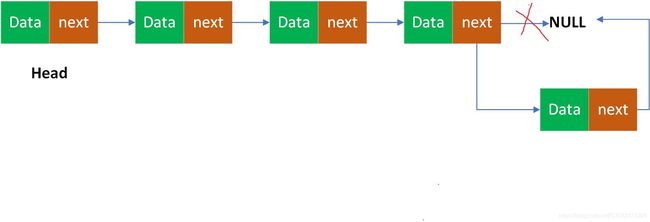
   第一步先遍历链表，找到最后一个节点之后，把最后一个节点的next指针赋值给新节点的next，也就是新节点的next指向了NULL，然后最后一个节点的next指向新节点。这样就插入成功，代码如下：

/**
		* @brief  单链表尾部添加
		* @param  
		* @retval 
		*/ 
		int single_link_tail_add(struct single_link *link, Elemtype item)
		{
			//申请一个新节点
			struct single_link *node = NULL;
			node = (struct single_link *)malloc(sizeof(struct single_link));
			if(node == NULL)
				return -1;
				
			node->data = item;		//填充数据


			//遍历数据，找到尾节点
			struct single_link * pNext = link;
			while(pNext->next != NULL)  //不等于空继续循环
			{
				pNext = pNext->next;
			}

			//现在执行插入操作
			node->next = pNext->next;
			pNext->next = node;
			link->data++;
			
			return 0;
		}

头插法：

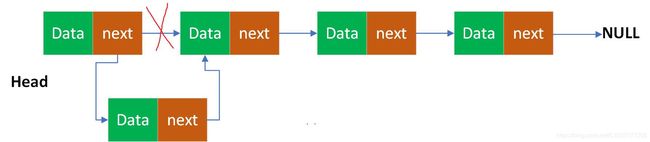
头插法其实跟尾插法逻辑差不多，只不过尾插法是要遍历到链表尾部，头插法就用头节点即可。
代码如下：

/**
		* @brief  单链表头部添加
		* @param  
		* @retval 
		*/ 
		int single_link_head_add(struct single_link *link, Elemtype item)
		{
			//申请一个新节点
			struct single_link *node = NULL;
			node = (struct single_link *)malloc(sizeof(struct single_link));
			if(node == NULL)
				return -1;
				
			node->data = item;		//填充数据

			//头节点
			struct single_link * pNext = link;

			//现在执行插入操作
			node->next = pNext->next;
			pNext->next = node;
			link->data++;
			
			return 0;
		}

双链表以后有需要再增加，哈哈哈

2. 删
   删除操作一般都是传入一个值，判断这个值的节点的位置，然后进行删除。
   
   查询这个节点，直接看查了，这里直接讲删除，因为我们是用单链表，所以前一个节点的指针不能丢，丢了就就找不到了。

/**
		* @brief  删除一个节点
		* @param  
		* @retval 
		*/ 
		int single_link_remove(struct single_link *link, Elemtype item)
		{
			if(link == NULL)
				return -1;
	
			//遍历数据
			struct single_link * pNext = link;
			struct single_link * node = NULL;
			while(pNext->next != NULL) //不等于空继续循环
			{
				//判断next，是预先判断下一个值，是不是需要删除的
				if(pNext->next->data == item)  
					break;
				pNext = pNext->next;
			}
			//这个是拿到上一个节点的指针，所以要删除的节点是下一个
			node = pNext->next;
			//这个就是把下一个下一个指针赋值给现在的next
			pNext->next = pNext->next->next;
			link->data--;
			free(node);
			return 0;
		}

3. 改
   以后再写，就是查询到对应的位置，然后修改值。

4. 查
   以后再写，现在都不知道使用在啥场景。

5. 释放链表
   这里写基数排序的时候，就搞错了，调了半天才调出来，看来链表操作还是需要画图
   。释放链表其实跟上面的删除差不多，只不过是循环删除。

/**
		* @brief  删除链表，只剩下头节点
		* @param  
		* @retval 
		*/ 
		int single_link_delete(struct single_link *link)
		{
			if(link == NULL)
				return -1;
	
			//遍历数据
			struct single_link * pNext = link;
			struct single_link * node = NULL;
			//判断下一个不为空，就进入删除
			while(pNext->next != NULL) //不等于空继续循环
			{
				//删除的逻辑跟删除一个差不多
				node = pNext->next;
				pNext->next = pNext->next->next;
				link->data--;
				free(node);
			}
			
			return 0;
		}

3.1.4 循环链表

循环链表这里没什么可说的，就是尾指针不指向NULL，指向了头节点，就是这么简单。单双链表都可以循环。

3.1.5 附加：链表的面试题

1.单链表逆序
面试题比较喜欢出单链表逆序，可能一个单链表只有一个指针，逆序比较难把，所以经常考，浏览了一下别人的博客，这两篇写的还可以，可以参考参考。
https://blog.csdn.net/qq_39871576/article/details/80613365
https://blog.csdn.net/qq_33160790/article/details/54948745

不查不知道，一查吓一跳，然后单链表逆序有3种解法，

• 普通循环
  当然去面试就是用这种普通循环，确实有点难受，没有系统学习过的，就是吃亏，今天在这里补救补救。
  普通循环方法比较难受的就是逻辑处理，不过相通了之后就清楚了，为了协助理解还是需要画图：
  (1) 原链表：
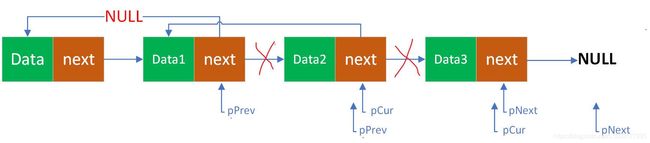
  (2) 链表逆序，只要是把next指针指向前面的data，每次调转一个指针，依次循环，下面按步骤进行：
  
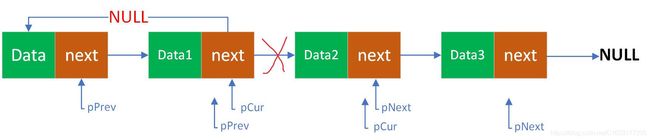
  这里要准备3个指针，pPrev指向前一个节点的指针，pCur指向当前节点的指针，pNext指向后一个节点的指针，所以要把pPrev赋值给pCur->next，因为刚开始pPrev是头节点，所以把pPrev设为NULL，所以pCur->next=NULL;然后把3个指针右移，这里要注意一个链表头节点next指针还指向data1

(3) 继续逆序

操作方式跟上一步一样

(4) 继续

操作步骤跟上面一样

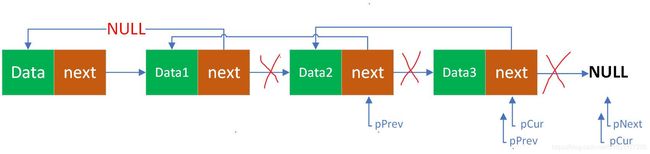
（5）处理头节点

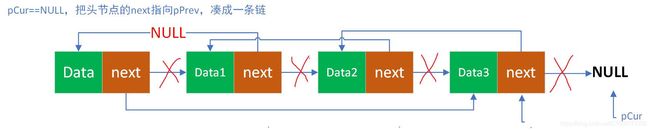
之前操作为了统一，没有对头节点做处理，现在操作完成了，把头节点的next指针指向左后一个节点，然后现在就形成了一条链表，导致逆序成功。下面是把其他东西删除后的结果

代码如下：

/**
		* @brief  单链表逆序，普通循环法
		* @param  
		* @retval 
		*/ 
		int single_link_reverse1(struct single_link *link)
		{
			if(link == NULL)
				return -1;
	
			//获取3个指针，前节点指针，当前节点指针，后节点指针
			struct single_link *pPrev, *pCur, *pNext;

			//调转指针
			pPrev = NULL;   		//默认开始为NULL，把头节点断开
			pCur = link->next;		

			while(pCur != NULL) 		//判断当前指针不为空
			{
				pNext = pCur->next;     //保存后节点指针
				pCur->next = pPrev;		//pCur->next指向头节点
				pPrev = pCur;			//前节点指针右移
				pCur = pNext;			//当前节点指针右移
			}
			
			//处理头节点,把最后一个节点挂接在头节点next指针
			link->next = pPrev;
			
			printf("pPrev %p %p %p %p\n", pPrev, pPrev->next, pPrev->next->next, pPrev->next->next->next);
			return 0;
		}

• 头插法
• 递归

2.判断单链表是否有环
参考《漫画算法》
准备两个指针，一个指针一次后移一个节点，一个指针一次后移两个节点，如果相遇说明链表有环，这相当于两个运动员在操场跑步，快的运动员总会追上慢的运动员，这就是判断链表是否有环。

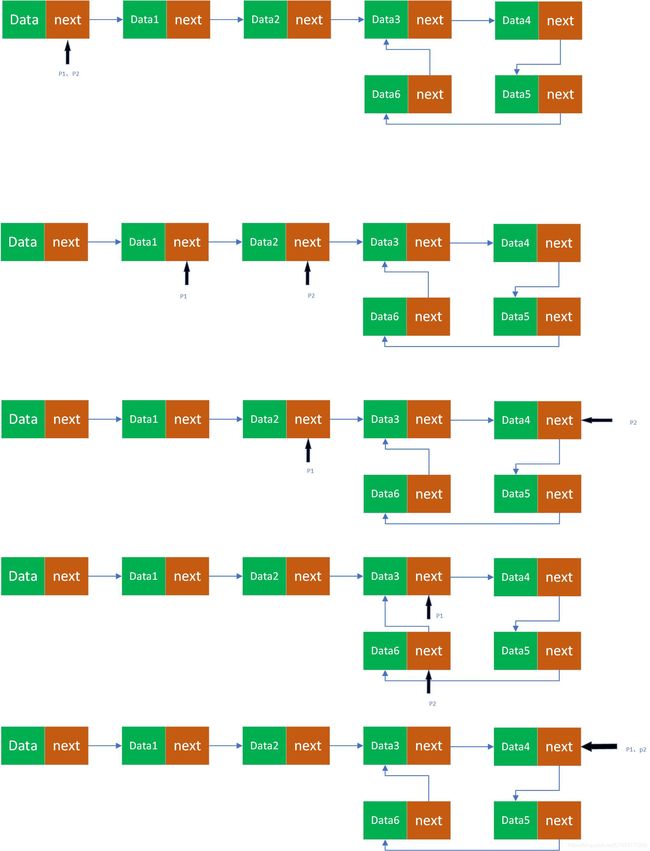
上面就是两个指针移动的示意图，如果链表有环就一定会相遇
下面时实现代码：

/**
		* @brief  判断单链表是否有环
		* @param  
		* @retval =1表示链表有环，=0表示链表没环
		* @idea	  准备两个指针，一个指针一次后移一个节点，一个指针一次后移两个节点，
				  如果相遇说明链表有环，快的指针会碰到或者超越慢的指针
		*/ 
		int single_link_isCycle(struct single_link *link)
		{
			if(link == NULL)
				return -1;

			//1.申请2个指针
			struct single_link *p1 = link;
			struct single_link *p2 = link;

			//2.开始遍历链表，查询是否有环
			while(p1 && p1->next)
			{
				p1 = p1->next->next;    //一次后移两个节点
				p2 = p2->next;			//一次后移一个节点
				if(p1 == p2)
					return 1;
			}
			
			return 0;
		}

扩展问题：
（1）如果链表有环，环的长度：
当两个指针首次想遇，证明链表有环的时候，让两个指针从相遇点继续循环前进，并统计前进的循环次数，直到两个指针第2次相遇，此时，统计出来的前进次数就是环长。
因为指针p1每次走1步，指针p2每次走2步，两者的速度差1步，当两个指针再次相遇时，p2比p1多走了整整1圈。因此，环长=每一次速度差X前进次数=前进次数。
来自《漫画算法》

简单代码如下：

/**
		* @brief  单链表的环长
		* @param  
		* @retval 环的长度
		*/ 
		int single_link_cycle_len(struct single_link *link)
		{
			if(link == NULL)
				return -1;
	
			//1.申请2个指针
			struct single_link *p1 = link;
			struct single_link *p2 = link;
			int cycle_len = 0, flag = 0;
			
			//2.开始遍历链表，查询是否有环
			while(p1 && p1->next)
			{
				p1 = p1->next->next;	//一次后移两个节点
				p2 = p2->next;			//一次后移一个节点
				if((p1 == p2) || flag)
				{
					if(p1 == p2 && flag)
						break;
					(flag) ? (cycle_len++):(flag=1);
				}
			}
	
			printf("cycle_len = %d\n", cycle_len);
			return cycle_len;
		}

（2）如果链表有环，求入环点（来自《漫画算法》）

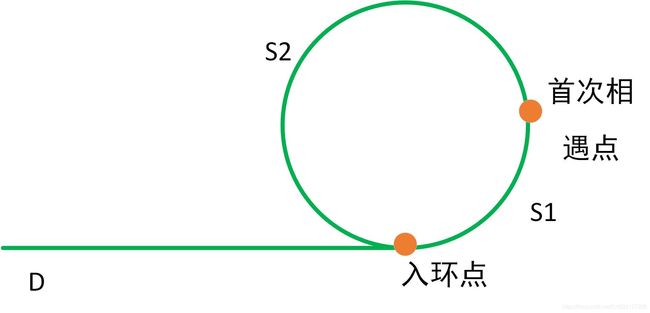
上图是对有环链表所做的一个抽象示意图。假设从链表头节点到入环点的距离是D，从入环点到两个指针首次相遇点的距离为S1,从首次相遇点回到入环点的距离是S2。
那么，当两个指针首次相遇时，各自所走的距离是多少呢？
指针p1一次只走1步，所走的距离是D+S1。
指针p2一次走2步，多走了1整圈，所走的距离是D+S1+S2+S1=D+2S1+S2。
由于p2的速度是p1的2倍，所以所走距离也是p1的2倍，因此
2(D+S1) =D+2S1+S2
等式经过整理得出：
D=S2

也就是说，从链表头节点到入环点的距离，等于从首次相遇点回到入环点的距离。
这样一来，只要把其中一个指针放回到头节点位置，另一个指针保持在首次相遇点，两个指针都是每次向前走1步。那么，它们最终相遇的节点，就是入环节点。

代码如下：

/**
		* @brief  单链表入环点
		* @param  
		* @retval 入环点
		*/ 
		int single_link_cycle_point(struct single_link *link)
		{
			if(link == NULL)
				return -1;
	
			//1.申请2个指针
			struct single_link *p1 = link;
			struct single_link *p2 = link;
			struct single_link *p3 = link;
			
			//2.开始遍历链表，查询是否有环
			while(p1 && p1->next)
			{
				p1 = p1->next->next;	//一次后移两个节点
				p2 = p2->next;			//一次后移一个节点
				if(p1 == p2)
				{
					break;
				}
			}

			//3.再由一个指针从头节点开始后移，p2指针继续后移两个指针相遇时，就是入环点
			while(p2 && p3)
			{
				p2 = p2->next;
				p3 = p3->next;
				if(p2 == p3)
					break;
			}

			printf("cycle_len = %d\n", p2->data);
			return p2->data;
		}

3.合并两条单链表
以后再搞