GNN系列（一）：简单图论&环境配置&PyG库

GNN系列（一）—简单图论&环境配置&PyG库

  图卷积神经网络（GCN）是近年兴起的基于图结构的广义神经网络结构，图论中抽象意义上的图可以来表示非欧几里得机构化数据。本小节从三个部分开始图神经网络的学习和介绍：

• 图论概念引入
• 所需环境搭建
• PyG相关库的学习

一、图论部分

  该部分主要介绍图的基本概念和基本的定义定理，这也是图与网络的基础。
定义1：图（Graph）
  一集元素及它们之间的某种关系。具体地说，图是一个二元组 $\mathcal{G}=\{\mathcal{V},\mathcal{E}\}$，其中集合 $\mathcal{V}$称为 顶点集，集合 $\mathcal{E}$是 $\mathcal{V}$ 中元素组成的某些无序对的集合，称为 边集。其中， $\mathcal{V}=\left\{v_1,\dots ,v_N\right\}$是所有顶点的集合， $\mathcal{E}=\left\{e_1,\dots ,e_M\right\}$ 是数量为 $M$ 的边的集合。
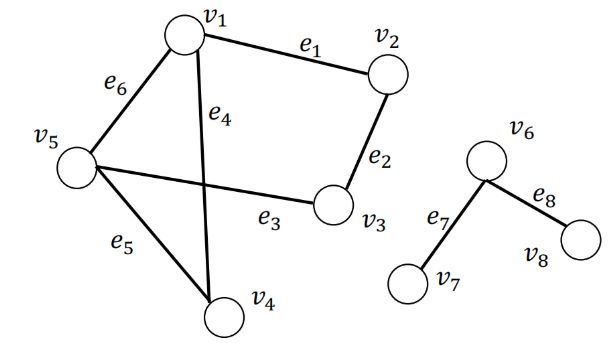
如下图是一个图的例子：

  在现实世界中图可以用来表示实体之间的关系；节点和边的信息可以是 类别型的（categorical），类别型数据的取值只能是哪一类别。一般称类别型的信息为 标签（label）；节点和边的信息可以是 数值型的（numeric），类别型数据的取值范围为实数。一般称类别型的信息为 属性（attribute）；大部分情况中，节点含有信息，边可能含有信息。
定义二（图的邻接矩阵）：
  给定一个图 $\mathcal{G}=\{\mathcal{V},\mathcal{E}\}$，其对应的 邻接矩阵被记为 $\mathbf{A}\in \{0,1{\}}^{N\times N}$。 ${\mathbf{A}}_{i,j}=1$表示存在从结点 $v_i$到 $v_j$的边，反之表示不存在从结点 $v_i$到 $v_j$的边。注意：在 无向图中，从结点 $v_i$到 $v_j$的边存在，意味着从结点 $v_j$到 $v_i$的边也存在。因而 无向图的邻接矩阵是对称的。在 无权图中， 各条边的权重被认为是等价的，即认为 各条边的权重为$1$。对于 有权图，其对应的邻接矩阵通常被记为 $\mathbf{W}\in \{0,1{\}}^{N\times N}$，其中 ${\mathbf{W}}_{i,j}=w_{ij}$表示从结点 $v_i$到 $v_j$的边的权重。若边不存在时，边的权重为 $0$。
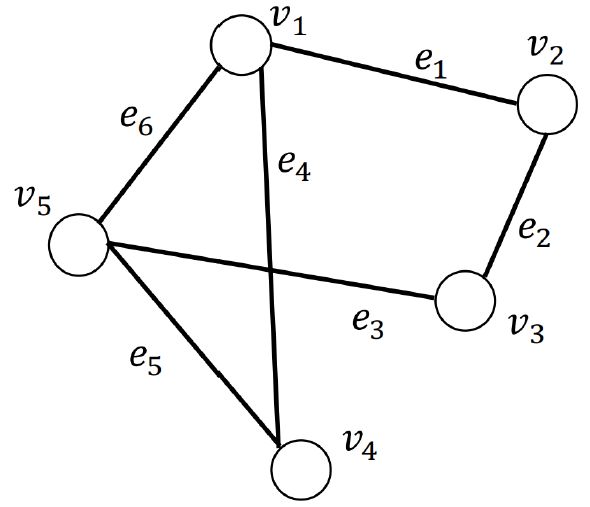
在上图中，邻接矩阵为：
$$\mathbf{A}=\left(\begin{array}{lllll}0& 1& 0& 1& 1\\ 1& 0& 1& 0& 0\\ 0& 1& 0& 0& 1\\ 1& 0& 0& 0& 1\\ 1& 0& 1& 1& 0\end{array}\right)$$
定义三（结点的度，degree）：

• 对于有向有权图，结点$v_i$的出度（out degree）等于从$v_i$出发的边的权重之和，结点$v_i$的入度（in degree）等于从连向$v_i$的边的权重之和。
• 无向图是有向图的特殊情况，结点的出度与入度相等。
• 无权图是有权图的特殊情况，各边的权重为$1$，那么结点$v_i$的出度（out degree）等于从$v_i$出发的边的数量，结点$v_i$的入度（in degree）等于从连向$v_i$的边的数量。
• 结点$v_i$的度记为$d(v_i)$，入度记为$d_{in}(v_i)$，出度记为$d_{out}(v_i)$。

定义四（邻接结点，neighbors）：
   结点$v_i$的邻接结点为与结点$v_i$直接相连的结点，其被记为$\mathcal{N}(v_i)$。 结点$v_i$的$k$跳远的邻接节点 （neighbors with $k$-hop） 指的是到结点$v_i$要走$k$步的节点（一个节点的$2$跳远的邻接节点包含了自身）。
定义五（行走，walk）：
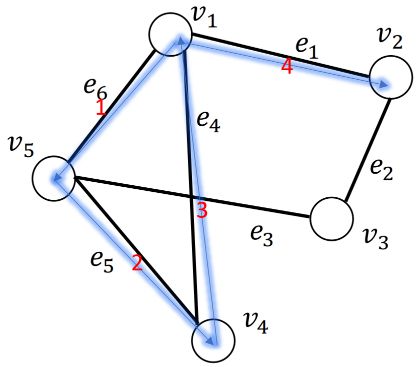
  $walk(v_1,v_2)=(v_1,e_6,e_5,e_4,e_1,v_2)$ ，这是一次“行走”，它是一次从节点 $v_1$ 出发，依次经过边 $e_6,e_5,e_4,e_1$ ，最终到达节点 $v_2$ 的“行走”。下图所示为 $walk(v_1,v_2)=(v_1,e_6,e_5,e_4,e_1,v_2)$ ，其中红色数字标识了边的访问序号。在“ 行走 ”中，节点是运行重复的。

定理六：

• 有一图，其邻接矩阵为 $\mathbf{A}$, ${\mathbf{A}}^n$为邻接矩阵的$n$次方，那么${\mathbf{A}}^n[i,j]$等于从结点$v_i$到结点$v_j$的长度为$n$的行走的个数。

定义七（路径，path）：

• “路径”是结点不可重复的“行走”。

定义八（子图，subgraph）：

• 有一图$\mathcal{G}=\{\mathcal{V},\mathcal{E}\}$，另有一图${\mathcal{G}}^{\prime }=\{{\mathcal{V}}^{\prime },{\mathcal{E}}^{\prime }\}$，其中${\mathcal{V}}^{\prime }\in \mathcal{V}$，${\mathcal{E}}^{\prime }\in \mathcal{E}$并且${\mathcal{V}}^{\prime }$不包含${\mathcal{E}}^{\prime }$中未出现过的结点，那么${\mathcal{G}}^{\prime }$是$\mathcal{G}$的子图。

定义九（连通分量，connected component）：

   给定图${\mathcal{G}}^{\prime }=\{{\mathcal{V}}^{\prime },{\mathcal{E}}^{\prime }\}$是图$\mathcal{G}=\{\mathcal{V},\mathcal{E}\}$的子图。记属于图$\mathcal{G}$但不属于${\mathcal{G}}^{\prime }$图的结点集合记为$\mathcal{V}/{\mathcal{V}}^{\prime }$ 。如果属于${\mathcal{V}}^{\prime }$的任意结点对之间存在至少一条路径，但不存在一条边连接属于${\mathcal{V}}^{\prime }$的结点与属于$\mathcal{V}/{\mathcal{V}}^{\prime }$的结点，那么图${\mathcal{G}}^{\prime }$是图$\mathcal{G}$的连通分量。

左右两边子图都是整图的连通分量。

定义十（连通图，connected graph）：

• 当一个图只包含一个连通分量，即其自身，那么该图是一个连通图。

定义十一（最短路径，shortest path）：

• $v_s,v_t\in \mathcal{V}$ 是图$\mathcal{G}=\{\mathcal{V},\mathcal{E}\}$上的一对结点，结点对$v_s,v_t\in \mathcal{V}$之间所有路径的集合记为${\mathcal{P}}_{\mathrm{s}\mathrm{t}}$。结点对$v_s,v_t$之间的最短路径$p_{\mathrm{s}t}^{\mathrm{s}\mathrm{p}}$为${\mathcal{P}}_{\mathrm{s}\mathrm{t}}$中长度最短的一条路径，其形式化定义为
  $$p_{\mathrm{s}t}^{\mathrm{s}\mathrm{p}}=\arg \underset{p\in {\mathcal{P}}_{\mathrm{s}\mathrm{t}}}{\min }|p|$$
  其中，$p$表示${\mathcal{P}}_{\mathrm{s}\mathrm{t}}$中的一条路径，$|p|$是路径$p$的长度。

定义十二（直径，diameter）：

• 给定一个连通图$\mathcal{G}=\{\mathcal{V},\mathcal{E}\}$，其直径为其所有结点对之间的最短路径的最小值，形式化定义为

$$\mathrm{diameter}(\mathcal{G})=\underset{v_s,v_t\in \mathcal{V}}{\max }\underset{p\in {\mathcal{P}}_{st}}{\min }|p|$$

定义十三（拉普拉斯矩阵，Laplacian Matrix）：

• 给定一个图$\mathcal{G}=\{\mathcal{V},\mathcal{E}\}$，其邻接矩阵为$A$，其拉普拉斯矩阵定义为$\mathbf{L}=\mathbf{D}-\mathbf{A}$，其中$\mathbf{D}=\mathbf{d}\mathbf{i}\mathbf{a}\mathbf{g}(\mathbf{d}({\mathbf{v}}_1),\cdots ,\mathbf{d}({\mathbf{v}}_{\mathbf{N}}))$。

定义十四（对称归一化的拉普拉斯矩阵，Symmetric normalized Laplacian）：

• 给定一个图$\mathcal{G}=\{\mathcal{V},\mathcal{E}\}$，其邻接矩阵为$A$，其规范化的拉普拉斯矩阵定义为

$$\mathbf{L}={\mathbf{D}}^{-\frac{1}{2}}(\mathbf{D}-\mathbf{A}){\mathbf{D}}^{-\frac{1}{2}}=\mathbf{I}-{\mathbf{D}}^{-\frac{1}{2}}\mathbf{A}{\mathbf{D}}^{-\frac{1}{2}}$$

二、环境配置

  本小节采用Anaconda+vs code+pytorch配置图神经网络的运行环境。首先确保pytorch环境能正常运行，可以通过GPU或者CPU来进行配置pytorch，具体配置过程参考pytorch官网,这里不过多介绍。通过如下代码看其版本号：

import torch
print(torch.__version__)

  配置图神经网络相关库PyG：PyTorch Geometric (PyG)是面向几何深度学习的PyTorch的扩展库，几何深度学习指的是应用于图和其他不规则、非结构化数据的深度学习。基于PyG库，我们可以轻松地根据数据生成一个图对象，然后很方便的使用它；我们也可以容易地为一个图数据集构造一个数据集类，然后很方便的将它用于神经网络。
CPU版的pytorch可通过如下的程序依次安装相应的包：

pip install torch-scatter -f https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html
pip install torch-sparse -f https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html
pip install torch-cluster -f https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html
pip install torch-spline-conv -f https://pytorch-geometric.com/whl/torch-1.8.0+cpu.html
pip install torch-geometric

Data类——PyG中图的表示及其使用

Data对象的创建

Data类的官方文档为torch_geometric.data.Data。
edge_index的每一列定义一条边，其中第一行为边起始节点的索引，第二行为边结束节点的索引。这种表示方法被称为COO格式（coordinate format），通常用于表示稀疏矩阵。PyG不是用稠密矩阵$\mathbf{A}\in \{0,1{\}}^{|\mathcal{V}|\times |\mathcal{V}|}$来持有邻接矩阵的信息，而是用仅存储邻接矩阵$\mathbf{A}$中非$0$元素的稀疏矩阵来表示图。

通常，一个图至少包含x, edge_index, edge_attr, y, num_nodes5个属性，当图包含其他属性时，我们可以通过指定额外的参数使Data对象包含其他的属性：

graph = Data(x=x, edge_index=edge_index, edge_attr=edge_attr, y=y, num_nodes=num_nodes, other_attr=other_attr)

获取Data对象属性

x = graph_data['x']

设置Data对象属性

graph_data['x'] = x

获取Data对象包含的属性的关键字

graph_data.keys()

对边排序并移除重复的边

graph_data.coalesce()

Data对象的其他性质

我们通过观察PyG中内置的一个图来查看Data对象的性质：

from torch_geometric.datasets import KarateClub

dataset = KarateClub()
data = dataset[0]  # Get the first graph object.
print(data)
print('==============================================================')

# 获取图的一些信息
print(f'Number of nodes: {data.num_nodes}') # 节点数量
print(f'Number of edges: {data.num_edges}') # 边数量
print(f'Number of node features: {data.num_node_features}') # 节点属性的维度
print(f'Number of node features: {data.num_features}') # 同样是节点属性的维度
print(f'Number of edge features: {data.num_edge_features}') # 边属性的维度
print(f'Average node degree: {data.num_edges / data.num_nodes:.2f}') # 平均节点度
print(f'if edge indices are ordered and do not contain duplicate entries.: {data.is_coalesced()}') # 是否边是有序的同时不含有重复的边
print(f'Number of training nodes: {data.train_mask.sum()}') # 用作训练集的节点
print(f'Training node label rate: {int(data.train_mask.sum()) / data.num_nodes:.2f}') # 用作训练集的节点的数量
print(f'Contains isolated nodes: {data.contains_isolated_nodes()}') # 此图是否包含孤立的节点
print(f'Contains self-loops: {data.contains_self_loops()}')  # 此图是否包含自环的边
print(f'Is undirected: {data.is_undirected()}')  # 此图是否是无向图

 

四、Dataset类——PyG中图数据集的表示及其使用

PyG内置了大量常用的基准数据集，接下来我们以PyG内置的Planetoid数据集为例，来学习PyG中图数据集的表示及使用。

Planetoid数据集类的官方文档为torch_geometric.datasets.Planetoid。
 

生成数据集对象并分析数据集

  如下方代码所示，在PyG中生成一个数据集是简单直接的。在第一次生成PyG内置的数据集时，程序首先下载原始文件，然后将原始文件处理成包含Data对象的Dataset对象并保存到文件。

from torch_geometric.datasets import Planetoid
dataset = Planetoid(root='/dataset/Cora', name='Cora')
len(dataset) #1
dataset.num_classes #7
dataset.num_node_features #1433

 

分析数据集中样本

可以看到该数据集只有一个图，包含7个分类任务，节点的属性为1433维度。

data = dataset[0]
# Data(edge_index=[2, 10556], test_mask=[2708],train_mask=[2708], val_mask=[2708], x=[2708,1433], y=[2708])
data.is_undirected()# True
data.train_mask.sum().item()# 140
data.val_mask.sum().item()# 500
data.test_mask.sum().item()# 1000

  现在我们看到该数据集包含的唯一的图，有2708个节点，节点特征为1433维，有10556条边，有140个用作训练集的节点，有500个用作验证集的节点，有1000个用作测试集的节点。
 

数据集的使用

  在学习了 PyTorch Geometric 中的数据处理、数据集、加载器和转换之后，是时候实现第一个图神经网络了！

import torch
from torch_geometric.datasets import Planetoid #加载 Cora 数据集
dataset = Planetoid(root='./tmp/Cora', name='Cora')
import torch.nn.functional as F
from torch_geometric.nn import GCNConv
#实现一个两层的 GCN
class Net(torch.nn.Module):
   def __init__(self):
       super(Net, self).__init__()
       self.conv1 = GCNConv(dataset.num_node_features, 16)
       self.conv2 = GCNConv(16, dataset.num_classes)

   def forward(self, data):
       x, edge_index = data.x, data.edge_index
       x = self.conv1(x, edge_index)
       x = F.relu(x)
       x = F.dropout(x, training=self.training)
       x = self.conv2(x, edge_index)

       return F.log_softmax(x, dim=1)
/*  
构造函数定义两个GCNConv层，在网络前向传递中被调用。非线性并未集成到conv调用中,
 需要在之后应用。使用 ReLU 作为中间非线性，并类数上输出一个 softmax 分布。
 在训练节点上训练这个模型 200 个 epochs：
*/
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net().to(device)
data = dataset[0]
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)

model.train()
for epoch in range(200):
   optimizer.zero_grad()
   out = model(data)
   loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
   loss.backward()
   optimizer.step()

model.eval()
_, pred = model(data).max(dim=1)
correct = int(pred[data.test_mask].eq(data.y[data.test_mask]).sum().item())
acc = correct / int(data.test_mask.sum())
print('Accuracy: {:.4f}'.format(acc))

最后输出结果为：

Accuracy: 0.8090

 
 
 

参考资料

• [1] Pytorch geometric
• [2]Chapter 2 - Foundations of Graphs, Deep Learning on Graphs
• [3]Datawhale图神经网络开源讲义