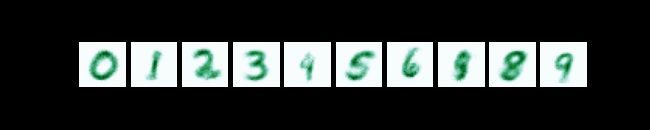CVAE (条件 变分 自动编码器)
notations
- x x x image
- z z z latent
- y y y label (omitted to lighten notation)
- p ( x ∣ z ) p(x|z) p(x∣z) decoder
Encoder - q ( z ∣ x ) q(z|x) q(z∣x) encoder
Decoder - p ^ ( h ) \hat{p}(h) p^(h) prior encoder (by variational inference)
PriorEncoder
model structure
class CVAE(nn.Module):
def __init__(self, config):
super(CVAE, self).__init__()
self.encoder = Encoder(...)
self.decoder = Decoder(...)
self.priorEncoder = PriorEncoder(...)
def forward(self, x, y):
x = x.reshape((-1, 784)) # MNIST
mu, sigma = self.encoder(x, y)
prior_mu, prior_sigma = self.priorEncoder(y)
z = torch.randn_like(mu)
z = z * sigma + mu
reconstructed_x = self.decoder(z, y)
reconstructed_x = reconstructed_x.reshape((-1, 28, 28))
return reconstructed_x, mu, sigma, prior_mu, prior_sigma
def infer(self, y):
prior_mu, prior_sigma = self.priorEncoder(y)
z = torch.randn_like(prior_mu)
z = z * prior_sigma + prior_mu
reconstructed_x = self.decoder(z, y)
return reconstructed_x
#
class Loss(nn.Module):
def __init__(self):
super(Loss,self).__init__()
self.loss_fn = nn.MSELoss(reduction='mean')
self.kld_loss_weight = 1e-5
def forward(self, x, reconstructed_x, mu, sigma, prior_mu, prior_sigma):
mse_loss = self.loss_fn(x, reconstructed_x)
kld_loss = torch.log(prior_sigma / sigma) + (sigma**2 + (mu - prior_mu)**2) / (2 * prior_sigma**2) - 0.5
kld_loss = torch.sum(kld_loss) / x.shape[0]
loss = mse_loss + self.kld_loss_weight * kld_loss
return loss
#
def train(model, criterion, optimizer, data_loader, config):
train_task_time_str = time_str()
for epoch in range(config.num_epoch):
loss_seq = []
for step, (x,y) in tqdm(enumerate(data_loader)):
# -------------------- data --------------------
x = x.to(device)
y = y.to(device)
# -------------------- forward --------------------
reconstructed_x, mu, sigma, prior_mu, prior_sigma = model(x, y)
loss = criterion(x, reconstructed_x, mu, sigma, prior_mu, prior_sigma)
# -------------------- log --------------------
loss_seq.append(loss.item())
# -------------------- backward --------------------
optimizer.zero_grad()
loss.backward()
optimizer.step()
# -------------------- end --------------------
logging.info(f'epoch {epoch:^5d} loss {sum(loss_seq[-config.batch_size:]) / config.batch_size:.5f}')
with torch.no_grad():
# -------------------- file --------------------
path = f'{config.save_fig_path}/{train_task_time_str}' # type(model).__name__
if not os.path.exists(path):
os.makedirs(path)
path += f'/epoch{epoch:04d}.png'
# -------------------- figure --------------------
plt.close()
fig, axs = plt.subplots(nrows=1, ncols=10, figsize=(10, 2), dpi=512)
fig.suptitle(f'epoch {epoch} loss {sum(loss_seq[-config.batch_size:]) / config.batch_size:.5f}')
# -------------------- infer --------------------
y = torch.Tensor(list(range(config.num_class)))
y = y.to(dtype=torch.int64)
y = nn.functional.one_hot(y, num_classes=config.num_class)
y = y.to(dtype=torch.float)
y = y.to(device)
x = model.infer(y)
x = x.cpu()
x = x.numpy()
x += x.min()
x /= x.max()
x *= 255
x = x.astype(np.uint8)
# -------------------- plot --------------------
for idx,ax,arr in zip(range(config.num_class),axs,x):
ax.set_title(str(idx))
ax.axis('off')
ax.imshow(arr.reshape((28,28)), cmap='BuGn')
# -------------------- save --------------------
# plt.show()
plt.savefig(path)
# -------------------- end --------------------
#
dynamics
- SGVB (stochastic_gradient + variational_bayesian) 框架根据 EM算法的原理 使用 变分推断 优化 ELBO.
- log p ( v ) = E L B O ( q ( z ∣ x ) , p ( x ∣ z ) ) + K L ( q ( z ∣ x ) ∥ p ( z ∣ x ) ) \log p(v) = \mathrm{ELBO} \left( q(z|x), p(x|z) \right) + \mathrm{KL} \left( q(z|x) \| p(z|x) \right) logp(v)=ELBO(q(z∣x),p(x∣z))+KL(q(z∣x)∥p(z∣x)) ELBO 是 对数似然 的代理.
- E L B O = E q ( z ∣ x ) [ log p ( x ∣ z ) p ( z ) ] + E n t r o p y ( q ( z ∣ x ) ) = E q ( z ∣ x ) [ log p ( x ∣ z ) ] − K L ( q ( z ∣ x ) ∥ p ( z ) ) \mathrm{ELBO} = \mathop{\mathbb{E}} \limits_{q(z|x)} \left[ \log p(x|z)p(z) \right] + \mathrm{Entropy} \left( q(z|x) \right) = \mathop{\mathbb{E}} \limits_{q(z|x)} \left[ \log p(x|z) \right] - \mathrm{KL} \left( q(z|x) \| p(z) \right) ELBO=q(z∣x)E[logp(x∣z)p(z)]+Entropy(q(z∣x))=q(z∣x)E[logp(x∣z)]−KL(q(z∣x)∥p(z))
- E q ( z ∣ x ) [ log p ( x ∣ z ) p ( z ) ] + E n t r o p y ( q ( z ∣ x ) ) \mathop{\mathbb{E}} \limits_{q(z|x)} \left[ \log p(x|z)p(z) \right] + \mathrm{Entropy} \left( q(z|x) \right) q(z∣x)E[logp(x∣z)p(z)]+Entropy(q(z∣x)) 用于证明EM算法的原理.
- E q ( z ∣ x ) [ log p ( x ∣ z ) ] − K L ( q ( z ∣ x ) ∥ p ( z ) ) \mathop{\mathbb{E}} \limits_{q(z|x)} \left[ \log p(x|z) \right] - \mathrm{KL} \left( q(z|x) \| p(z) \right) q(z∣x)E[logp(x∣z)]−KL(q(z∣x)∥p(z)) 用于神经网络优化.
- max E q ( z ∣ x ) [ log p ( x ∣ z ) ] ≈ sampling max q ( z i ∣ x i ) log p ( x i ∣ z i ) = opposite min c r o s s _ e n t r o p y _ l o s s ∼ substitution min m s e _ l o s s \max \mathop{\mathbb{E}} \limits_{q(z|x)} \left[ \log p(x|z) \right] \stackrel{\textsf{sampling}}{\approx} \max q(z_i|x_i) \log p(x_i|z_i) \stackrel{\textsf{opposite}}{=} \min \mathtt{cross\_entropy\_loss} \stackrel{\textsf{substitution}}{\sim} \min \mathtt{mse\_loss} maxq(z∣x)E[logp(x∣z)]≈samplingmaxq(zi∣xi)logp(xi∣zi)=oppositemincross_entropy_loss∼substitutionminmse_loss
- min K L ( q ( z ∣ x ) ∥ p ( z ) ) ≈ Variational Inference min K L ( q ( z ∣ x ) ∥ p ^ ( z ) ) \min \mathrm{KL} \left( q(z|x) \| p(z) \right) \stackrel{\textsf{Variational Inference}}{\approx} \min \mathrm{KL} \left( q(z|x) \| \hat{p}(z) \right) minKL(q(z∣x)∥p(z))≈Variational InferenceminKL(q(z∣x)∥p^(z))
kld_loss_weight = 1e-5
{'batch_size': 25,
'conv_encoder': True,
'learning_rate': 1e-05,
'num_class': 10,
'num_epoch': 16,
'save_fig_path': './figs',
'use_cuda': True}
以上这组超参数能较快的收敛到较优模型参数.
实验发现, batch_size较大时收敛到较差模型参数, learning_rate较小时收敛非常缓慢.
- 神经网络先学数字范围再学数字形状. epoch[0-3]数字有很多噪声点, epoch[4-15]数字呈平滑图形.
- 神经网络先学前景(数字)再学背景(白色). epoch[0-10]背景都是暗色, epoch[11-15]背景都是亮色.
- epoch11开始学最不重要的细节(白色背景), epoch12开始就逐渐发生了过拟合! 尤其是数字0, 在epoch15中看起来像数字8一样.