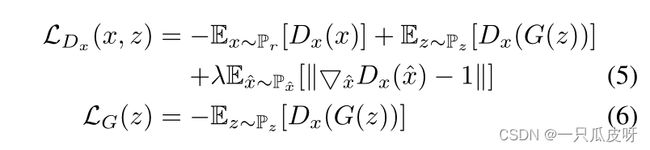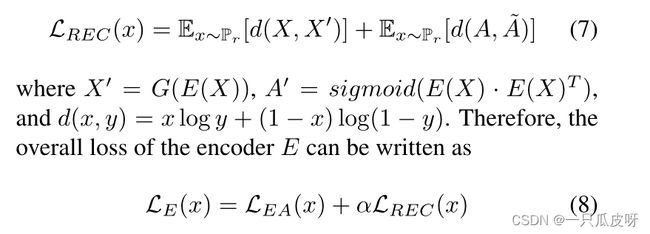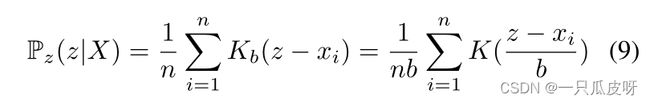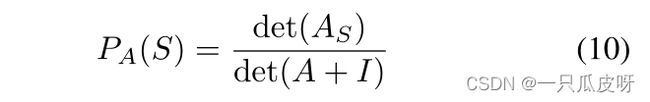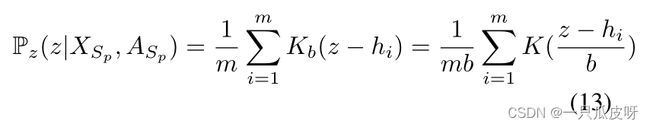【阅读笔记】Distribution-induced Bidirectional Generative Adversarial Network for Graph Representation
代码:GitHub - SsGood/DBGAN: [CVPR2020] Tensorflow implementation for paper ''Distribution-induced Bidirectional Generative Adversarial Network for Graph Representation Learning''![]() https://github.com/SsGood/DBGAN
https://github.com/SsGood/DBGAN
Abstract
图表示学习的目的是将一个图的所有节点编码成低维向量,作为许多计算视觉任务的输入。然而,现有的算法大多忽略了数据固有分布甚至噪声的存在。这可能会显著增加过拟合现象,降低测试精度。在本文中,我们提出了一种分布诱导的双向生成对抗网络(DBGAN),用于图表示学习。该算法采用结构感知的方法估计潜在表示的先验分布,而不是广泛使用的正态分布假设,通过原型学习隐式地连接图和特征空间。这样就为所有节点生成了有区别的鲁棒表示。此外,为了在保持表示能力的同时提高泛化能力,通过一个双向对抗学习框架很好地平衡了样本级和分布级的一致性。经过精心设计和展示的大量实验表明,我们的DBGAN在表示和鲁棒性之间取得了明显更好的平衡,同时在各种任务中具有显著的维数效率。
Introduction
图表示学习是解决这些问题的一种通用方法,其目的是将图节点的稀疏原始特征表示为紧凑的低维向量,同时为后续下游任务保留足够的信息,如链接预测、聚类、推荐。近年来,各种图表示学习方法被提出,大致可以归纳为两类:基于邻近性的算法和基于深度学习的算法。
GraRep、HOPE、M-NMF等基于邻近性的算法,通过矩阵分解尝试对图邻接矩阵进行分解,得到节点表示。而对于概率模型,如DeepWalk、line和node2vec,它们通过随机漫步和各种顺序邻近性学习具有局部邻域连接的节点表示。这些方法都注重在低维空间中保持原始邻域关系。最近的研究也表明,概率模型和基于矩阵分解的算法是等价的,可以用一个统一的模型来实现。
基于深度学习的方法受到越来越多的关注,其中大多数使用自编码器框架来捕获潜在的表示。SDNE和DNGR使用深度自编码器对正点互信息(PPMI)进行建模,同时保持图的结构。GAE首先将GCN作为编码器合并到自动编码器框架中,通过重构邻接矩阵来寻找潜在的表示。此外MGAE、GDN和GALA试图通过在GAE基础上构建可学习的译码器和编码器来保持潜在表示中的节点特征。
实际上,上述方法大多是对邻接矩阵或节点特征进行重构,而不是同时对两者进行重构。然而,对于良好的低维潜在表示,需要同时保留图的拓扑结构和节点特
值得注意的是,上述方法都没有明确地利用图数据的潜在分布,因此不能很好地保持跨域(图空间和特征空间)的分布一致性,导致表示的泛化性差,对噪声敏感。由于生成式对抗网络(GAN)[12]具有较强的分布拟合能力,一些研究将对抗学习引入图表示学习领域,以提高学习后的潜在表示的性能。在GraphGAN[38]和ProGAN[10]中,生成的假节点对和节点三联体与真实数据竞争,增强了潜在表示的鲁棒性。这些方法忽略了全局结构和节点特征,无法保持分布式一致性,导致泛化能力不足。此外,在AIDW[5]和ARGA[28]中,一般都假设正态分布N(0,1)来指导潜在表征的生成。但是,在大多数情况下,用N(0,1)来建模图数据的潜在分布是不合适的,一个不准确的先验分布会导致模型过平滑甚至误导。
Contributions
- 我们提出了一种分布诱导的双向生成对抗网络(DBGAN),用于具有维数高效特性的图表示学习。据我们所知,在对抗性学习中考虑先验分布估计是第一项工作。
- 为了在保持表示能力的同时提高泛化能力,通过双向对抗学习很好地平衡了样本级和分布级的一致性。
- 与广泛使用的正态分布假设不同,我们通过将图和特征空间与学习的原型连接起来,创新地估计潜在表示的结构感知先验分布,从而生成鲁棒性和判别性的表示。
- 对当前可用替代方案的重大改进表明,我们的 DBGAN 在图表示学习领域创建了一个新的基线。
用于表示学习的GAN
GAN自从 Goodfellow 首次提出以来,已经在各个领域展示了其强大的分布拟合能力。 AAE、BiGAN和 ALI已经探索了对抗学习在图像表示领域的应用。而最近,基于 BiGAN 的 BigBiGAN 在图像表示学习方面取得了惊人的表现。
上述工作的成功表明,GAN 的分布拟合能力不仅可以用于生成数据,还可以用于理解数据。因此,GAN 已经以各种形式被引入到图表示学习领域。
从样本生成的角度来看,丁等人使用生成器在子图之间的低密度区域生成假样本,使分类器能够考虑图数据的密度特征。为了保留结构信息,ProGAN应用生成器生成节点的三元组,以发现原始空间中的邻近性并将其保留在低维空间中。
从潜在分布拟合的角度来看,NetRA 使用对抗性学习使潜在表示远离正态分布产生的噪声表示,以提高表示的抗干扰能力。如图1所示,ARGA 和AIDW采用类似的方法,分别在[17]和[30]中引入对抗性学习,以提高表征的泛化能力。
上述方法虽然取得了良好的性能,但其缺点也很明显。 [6, 10, 38] 只考虑局部结构信息,忽略全局结构和分布一致性,导致噪声敏感性,这使得表示不太稳健。此外,在[5, 28]中,没有利用节点特征,预先假设的正态分布与现实中的复杂图数据并不理想地符合,这使得模型趋于过度平滑和进一步减少了学习到的潜在表示的泛化。
Method
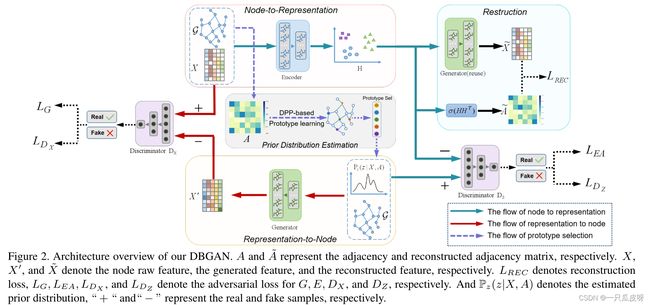
1. 在编码阶段,编码器 E 接受 A 和 X 作为输入并输出潜在表示矩阵 H。
2. 之后,E 和从先验分布 Pz|(X,A) 采样的数据 Z 输入到判别器 Dz 中进行对抗训练,其中 zi∈Z 和 hi∈H 分别为正样本和负样本。
3. 同时,生成器 G 接受 Z 和 A 作为输入并输出图的假特征矩阵 X',然后将 X' 作为负样本和 X 作为正样本发送到鉴别器 Dx 进行对抗训练。
4. 在重建阶段,H 被送到 G,然后输出重建的 X~。此外,H 通过重构过程~A = sigmoid(HHT) 重构为~A。
在这项工作中,我们使用 GCN [16] 作为编码器 E 和生成器 G,使用 MLP 作为鉴别器 Dz 和 Dx。
双向对抗学习
1、对抗损失
对抗性损失用于最小化两个分布之间的距离。这里我们使用中的 Wasserstein 距离(用来度量两个概率分布之间的差异)来衡量图数据分布 Pr(x) 与潜在表示 Pz(x) 的先验分布之间的差异,它可以定义为:
其中f表示判别函数,fL≤1表示判别函数需要满足Lipschitz常数为1的Lipschitz约束条件。这里使用 [14] 中提出的梯度惩罚项来实现 Lipschitz 约束,判别函数由判别器 Dz 学习。因此,Eq.(1) 可以作为 Dz 的目标,而 E 的目标则相反。
根据等式(1),我们可以定义 Dz 和 E 的对抗性损失如下:
其中 ˆz 表示从 Pz 采样的 E(x) 和 z 的随机插值。当 E 更新时,Dz 不会改变。因此,方程(3)中的Ez∼Pz [Dz(z)]不会为E提供梯度,那么方程(3)可以简化为:
同样,通过切换 Pz 和 Px 的角色,我们可以得到 G 和 Dx 的对抗性损失如下:
2、重构损失
除了保证图空间和原始特征空间之间分布级别一致性的对抗性损失之外,还强制执行重构损失 LREC(x) 以实现样本级别的一致性。
我们按照[17]中的设置从潜在表示中得到重建的邻接矩阵~A,这里的~A应该类似于真实的邻接矩阵A。此外,通过 G 建立的潜在表示到图数据的映射,我们可以得到重构的特征矩阵 X' = G(E(X))。重建损失可以定义如下:
潜在表示的先验分布损失
对于基于先验分布假设的方法,先验分布 Pz 对其性能至关重要。例如,对于多类别的图数据,用正态分布N(0, 1)作为Pz来表示图是不合理的。此外,通过双向对抗学习,适当的 Pz 可以提高表示的鲁棒性和可辨别性。由于除了给定的 A 和 X 之外,我们没有更多的先验,因此一种直观的方法是通过非参数估计方法(例如核密度估计 (KDE))估计近似于 Pz(z) 的 Pz(z|X)。另外,我们使用PCA对X进行降维,得到Xp = {xi}i=1,... ,n,然后我们可以得到Pz(z|X)如下:
其中 K(·) 是核函数,b 表示带宽,Kb(·) 是缩放后的核函数。
但是,这种直观的方法存在一些问题。首先,完全忽略了嵌入在 A 中的显式结构信息;其次,学习模型容易受到噪声 X 的影响,从而降低表示的鲁棒性。因此,我们可以使用 Pz(z|X, A) 而不是 Pz(z|X) 来近似 Pz(z)。
1、基于DPP的原型学习
对于异构的 A 和 X,直接获得 Pz(z|X, A) 并非易事。考虑到 A 和 X 虽然在不同的域中在结构上是一致的,我们可以利用跨域原型来桥接原始特征域和图域。因此 Pz(z|X, A) 可以替换为 Pz(z|XSp , ASp ),其中 Sp 表示原型的索引集。
基于DPP策略采样得到的点就更加 diverse一些,也就是让点与点之间尽量远一些, 少出现多个点聚在一起的情况。
对于原型学习,采用行列式点过程(DPP)[18]来选择多样化的原型子集。具体来说,邻接矩阵A被认为是度量矩阵。给定一个子集 VS⊆ V ,其项由 S⊆ N = {1, · · · , n} 索引,那么基于度量矩阵 A 的 S 的采样概率可以定义如下:
在矩阵A上,选择一个子集S,则S上的元素被选中的概率可由(10)计算。
其中I表示单位矩阵,AS≡[Aij]i,j∈S,det(·)表示矩阵的行列式。显然,这里定义的抽样概率是归一化的,因为:
根据式(10),将概率分配给 N 的任何子集,这将导致原型索引子集的搜索范围很大。因此,我们将子集大小限制为 |S| = m。当子集 S 的大小固定为 m 时,我们可以定义采样概率如下:
2、结构感知先验分布估计
根据原型索引集Sp与|Sp| = m,可以从X中采样一个节点特征矩阵Xp。然后,我们使用PCA对Xp进行降维得到Hp。
总而言之,通过 Eq.14 中的流程,我们获得了 Pz 的近似值,即 Pz(z|XSp , ASp )。