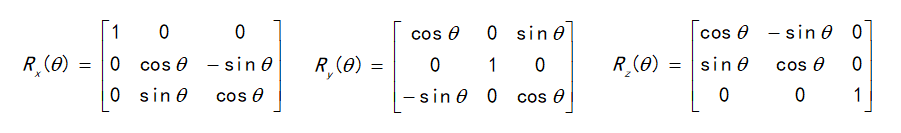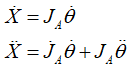机械臂阻抗控制
先上代码:https://github.com/lsk-gith/robot_impedance_control
初衷:
研三马上毕业,2019年入学,当年12月份就开始闹疫情,很多事情都当误了,不过自己以后也不从事这个行业了,并且现在论文也写完了,就把知识点总结一下,以帮助更多的人吧。
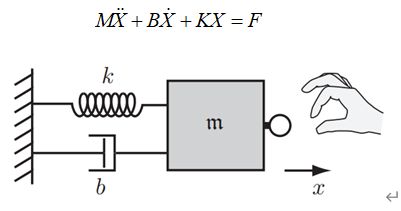
#动力学模型:
![]()
M C G项都是我们所熟知的,其求法近期会上传。
#阻抗原理:
弹簧阻尼模型这个我们都知道,所以也就不在啰嗦。
![]()
来替代X,毕竟是做轨迹跟踪,下标d是理想位姿,位姿速度和位姿加速度。
#阻抗和导纳:
阻抗控制中有人会把它分为阻抗和导纳,其实这些都是阻抗,只不过是实现方式不同而已,一个是基于力矩的一个是基于位置的。
######基于力矩的:
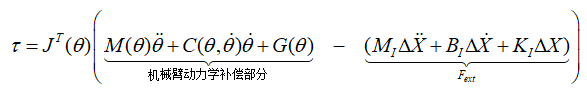
在基于力矩的阻抗控制中,一般通过关节位置编码器、转速表和加速度计用来采集得到关节角度角速度和角加速度变化,与规划的理想轨迹做差得出![]()
代入到阻抗模中,将这部分阻抗模型产生的力矩转换到关节空间的力矩就可以了,不需要末端安装六维力矩传感器。
######基于位置的:
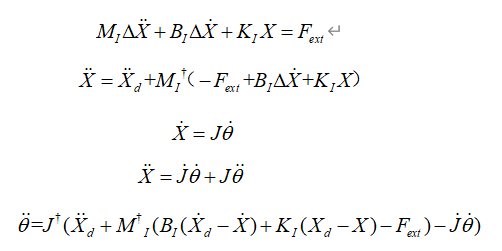
其中Fext就是六维力矩传感器采集得到的力,基于位置控制的不需要动力学模型,这一点也是很多人喜欢的,毕竟动力学模型的MCG系数很难求,一般需要CAD导出,若要更精确的需要参数辨识等。
#怎么在机械臂上实现:
这里不介绍基于关节空间的(单个关节实现阻抗模型,这个很简单不在叙述),全文所述都是基于笛卡尔空间的,目前已经知道了阻抗模型,那么问题来了怎么把阻抗模型使用到机械臂末端的位姿X上呢,以及机械臂末端位姿的△X,△Xd和△Xdd怎么计算?。
我们知道在三自由度以及一下的机械臂中,末端都只是位置变化,不涉及姿态变化,所以X,Xd,Xdd的求解就很简单,毕竟末端就只是xyz三个量表示,对其求导就是Xd,再次求导就是Xdd。
但是对于六轴甚至七轴的就不这么幸运了,末端是由位置和姿态组成,位置的计算还是可以遵循以上规则,但是姿态就不可以了,首先我们知道在一般的机器人运动学计算中末端姿态都是使用旋转矩阵计算的,由9个量组成,我们总不能将旋转矩阵求个导来计算Xd和Xdd吧,当然这是不现实的。
姿态最常用的表示方法就是欧拉角(具体定义,可以wiki或者百度),总的来说就是使用三个变量来表示一个唯一的旋转矩阵,其中还使用了正交矩阵的凯莱公式,推导如下:

下面以ZXZ的经典欧拉角为例介绍:
欧拉角按照旋转轴分为经典欧拉角(Proper Euler Angle)和泰特布莱恩角(Tait–Bryan angles),共 12种旋转方式:经典欧拉角-Proper Euler angles (z-x-z, x-y-x, y-z-y, z-y-z, x-z-x, y-x-y)使用两个轴的旋转角度表示,第一个旋转角度和第三个旋转角度都是绕同一个轴。泰特-布莱恩角-Tait–Bryan angles (x-y-z, y-z-x, z-x-y, x-z-y, z-y-x, y-x-z)使用三个轴的旋转角度表示。

其中红框里的矩阵很重要也是我们在计算分析雅各比矩阵时特别重要的部分。
其实计算红框里矩阵不必这么麻烦,在peter所编写的机器人工具箱中eul2jac()和rpy2jac()函数有关于该矩阵的计算,这里就班门弄斧了一下:
clear
clc
syms phi theta psi phid thetad psid A real
syms phit(t) thetat(t) psit(t)
order = 'zxz';
R = eul2r_my(phi, theta, psi, order)
Rt = eul2r_my(phit, thetat, psit, order);
dRdt = diff(Rt, t);
dRdt = subs(dRdt, {diff(phit(t),t), diff(thetat(t),t), diff(psit(t),t),}, {phid,thetad,psid});
dRdt = subs(dRdt, {phit(t),thetat(t),psit(t)}, {phi,theta,psi});
dRdt = formula(dRdt);
w = vex(dRdt * R');
w = simplify(w);
rpyd = [phid thetad psid];
for i=1:3
for j=1:3
C = coeffs(w(i), rpyd(j));
if length(C) == 1
A(i,j) = 0;
else
A(i,j) = C(2);
end
end
end
A
function rotmat = rotz(gamma)
rotmat = [cos(gamma) -sin(gamma) 0; sin(gamma) cos(gamma) 0; 0 0 1]
end
function rotmat = roty(beta)
rotmat = [cos(beta) 0 sin(beta); 0 1 0; -sin(beta) 0 cos(beta)]
end
function rotmat = rotx(alpha)
rotmat = [1 0 0;0 cos(alpha) -sin(alpha); 0 sin(alpha) cos(alpha)]
end
clear
clc
syms phi theta psi phid thetad psid A real
syms phit(t) thetat(t) psit(t)
order = 'zxz';
R = eul2r_my(phi, theta, psi, order)
Rt = eul2r_my(phit, thetat, psit, order);
dRdt = diff(Rt, t);
dRdt = subs(dRdt, {diff(phit(t),t), diff(thetat(t),t), diff(psit(t),t),}, {phid,thetad,psid});
dRdt = subs(dRdt, {phit(t),thetat(t),psit(t)}, {phi,theta,psi});
dRdt = formula(dRdt);
w = vex(dRdt * R');
w = simplify(w);
rpyd = [phid thetad psid];
for i=1:3
for j=1:3
C = coeffs(w(i), rpyd(j));
if length(C) == 1
A(i,j) = 0;
else
A(i,j) = C(2);
end
end
end
A
function rotmat = rotz(gamma)
rotmat = [cos(gamma) -sin(gamma) 0; sin(gamma) cos(gamma) 0; 0 0 1]
end
function rotmat = roty(beta)
rotmat = [cos(beta) 0 sin(beta); 0 1 0; -sin(beta) 0 cos(beta)]
end
function rotmat = rotx(alpha)
rotmat = [1 0 0;0 cos(alpha) -sin(alpha); 0 sin(alpha) cos(alpha)]
end
这样就可以计算分析雅各比矩阵来计算基于欧拉角的Xd了
#分析雅各比计算:
几何雅各比计算:
几何雅各比为矩阵为6X6的矩阵,分为两部分前三行代表位置,后三行代表姿态。
对于雅各比矩阵的计算:
方法一:
方法二:
使用peter机器人工具箱jacobian()函数,不在详细讲解。
分析雅各比计算:
将几何雅各比的两部分分为:
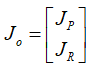
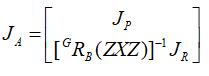
其中R(ZXZ)就是我们上面计算的红框矩阵。
#计算X,Xd,Xdd:
X 计算:
X的位置部分使用P

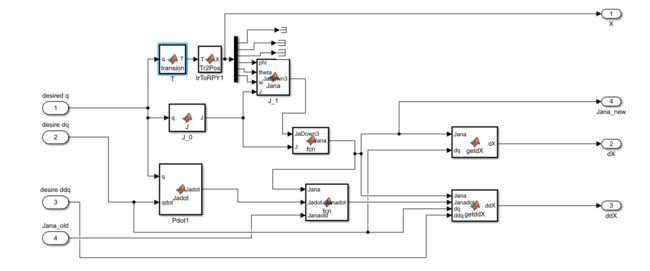
基于位置的阻抗控制实现:
代码地址:https://github.com/lsk-gith/robot_impedance_control
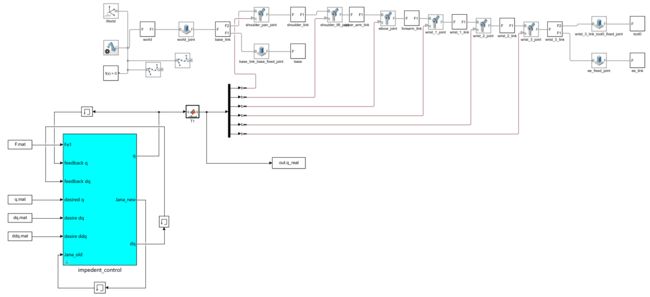
仿真代码:
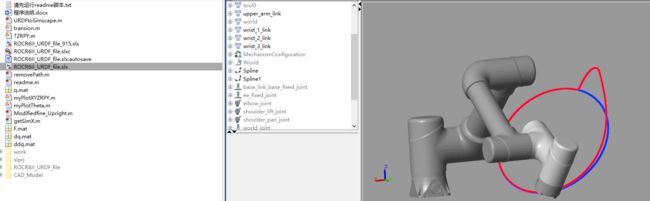
先看仿真结果:
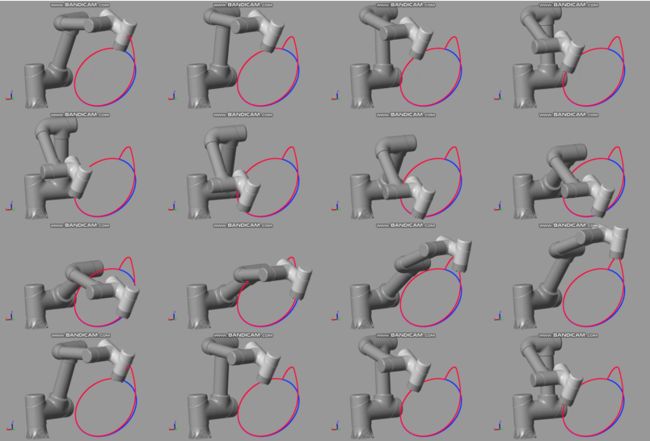
图中红色线条是实际运行轨迹,蓝色时理论轨迹。出现位置偏离是因为末端施加了一个外力,这个外力只维持了一段时间就撤销了。
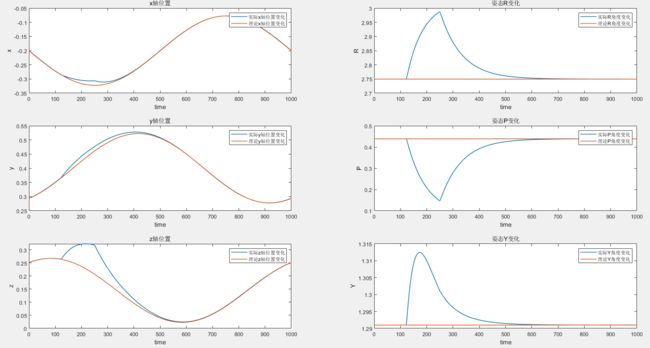
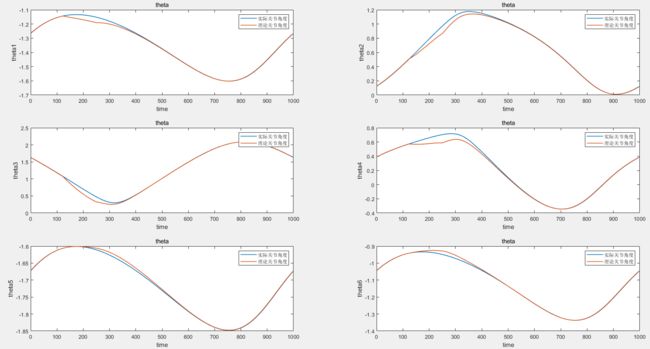
讨论其他表示位姿的方法:
欧拉角只是表示末端姿态的方法之一,可以表示末端姿态的方法有很多,我们先看看其他机械臂厂家如何表示末端姿态吧:目前常见的机械臂公司例如史陶比(Staubli)公司使用绕XYZ的泰特布莱恩角,爱得普(Adept)使用绕ZYZ的欧拉角,库卡(KUKA)使用绕ZYX的泰特布莱恩角,发那科(Fanuc)与安川(Motoman)则使用绕XYZ的泰特布莱恩角,ABB机器人使用四元数表达旋转,优傲(UR)机器人使用轴角。
四元数:
我们先来观摩Franka机器人使用的四元数代码(https://frankaemika.github.io/libfranka/cartesian_impedance_control_8cpp-example.html)。
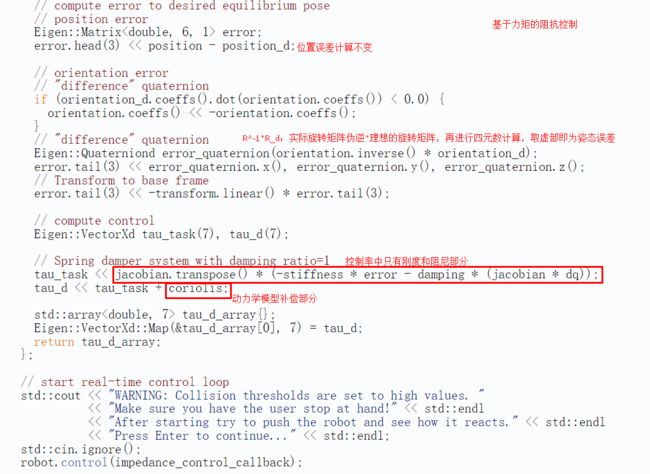

以上只是个人见解,如有错误也请多多保函,也不必联系我修改,毕竟之后不从事这个。
补充一下雅各比矩阵导数(Janadot)的求解方法,以及P导数(Pdot )的求解方法,:
%% load data
syms q_vec q1 q2 q3 q4 q5 q6 g real;
syms t t1(t) t2(t) t3(t) t4(t) t5(t) t6(t);
syms q1dot q2dot q3dot q4dot q5dot q6dot real;
syms t1dot(t) t2dot(t) t3dot(t) t4dot(t) t5dot(t) t6dot(t);
syms q1dotdot q2dotdot q3dotdot q4dotdot q5dotdot q6dotdot real;
syms t1dotdot(t) t2dotdot(t) t3dotdot(t) t4dotdot(t) t5dotdot(t) t6dotdot(t);
q_vec = [q1 q2 q3 q4 q5 q6].';
t_vec = [t1 t2 t3 t4 t5 t6].';
tdot_vec = [diff(t1(t),t) diff(t2(t),t) diff(t3(t),t) diff(t4(t),t) diff(t5(t),t) diff(t6(t),t)].';
tdotdot_vec = [diff(t1dot(t),t) diff(t2dot(t),t) diff(t3dot(t),t) diff(t4dot(t),t) diff(t5dot(t),t) diff(t6dot(t),t)].';
tdotsh_vec = [t1dot(t) t2dot(t) t3dot(t) t4dot(t) t5dot(t) t6dot(t)].';
tdotdotsh_vec = [t1dotdot(t) t2dotdot(t) t3dotdot(t) t4dotdot(t) t5dotdot(t) t6dotdot(t)].';
qdot_vec = [q1dot q2dot q3dot q4dot q5dot q6dot].';
qdotdot_vec = [q1dotdot q2dotdot q3dotdot q4dotdot q5dotdot q6dotdot].';
load(('.\InverseDynamic\MCG.mat'));
load(('.\kinematic\PR.mat'));
%% Forward Kinematics
P_fin = P; %Extracting only the x-y-z position from T matrix
P_fint = subs(P_fin,q_vec,t_vec); % substitute time dependence
Pdottemp = diff(P_fint,t); % Pdot differentiate w.r.t. time
Pdot = subs(Pdottemp,[t_vec,tdot_vec],[q_vec,qdot_vec]); % substitute time independence
R0tip = R;% rotation matrix of end point
% Initialize the robot at some position as home [0.5 0.5 0.2 0.2 0.2 0.2]';
% qHome = [pi/2.5 pi/6 1.5 1.2 pi/5 pi/7]';
load('.\Green2dai\data.mat');
thetalist = data(1:10:end,1:6);%N*6
dthetalist = data(1:10:end,7:12);
ddthetalist = data(1:10:end,13:18);
qHome = thetalist(1,:)';
% Calculate numerical transformation matrix
T_fin=[[R;0,0,0],[P;1]];
matlabFunction(T_fin,'File','transion');
THome = subs(T_fin,q_vec,qHome);
%% Geometric and Analytical Jacobian Calculation Calculate the first three rows of Jacobian (common to Analytical and Geometric Jacobians) J3 = jacobian(P_fin,q_vec)'Janasym','Janadot','Jgeom'
J3=J(1:3,1:6);
% omega = last three rows of geometric Jacobian as defined by axis of rotation with respect to the base frame.
omega1 = double(subs(J,q_vec,qHome));
omega=omega1(4:6,1:6);
% Combine to form the Geometric Jacobian Jgeom = [J3;omega];
Jgeom = J;
Jge = J;
matlabFunction(Jge,'File','Jge');
% Calculate rpy Angles from Transformation Matrix using Peter Corke's tr2eul function
eul = tr2rpy(THome);%
% roll-pitch-yaw, i am lazy, so i dont want to change the name!!!!
phi = eul(1);theta = eul(2);xi = eul(3);
% EUL2JAC Euler angle rate Jacobian, this can reference the eul2jac.m function.
om2eulmat = [cos(theta)*cos(xi), -sin(xi), 0;cos(theta)*sin(xi), cos(xi), 0;-sin(theta), 0, 1];
euldot = om2eulmat\omega;
% Symbolic Analytical Jacobian
Janasym = [J3;euldot];
% Symbolic First derivative of Analytical Jacobian
Janadot = subs(diff(subs(Janasym,q_vec,t_vec),t),[t_vec,tdot_vec],[q_vec,qdot_vec]);
Jdot = subs(diff(subs(J,q_vec,t_vec),t),[t_vec,tdot_vec],[q_vec,qdot_vec]);
JanadotUp3 = Jdot(1:3,:);
matlabFunction(JanadotUp3,'File','JanadotUp3');
%% Initialize variables for iterations
j=0;
% iter = 0:dt:time;
dt = 0.02;
iter = size(thetalist,1);
qnew=qHome;
q=qnew;
% qdotnew = [0 0 0 0 0 0]';
qdotnew = dthetalist(1,:)';
euldot_old = euldot;
% traj_des_theta = [qHome(1).*ones(size(iter,2),1),qHome(2).*ones(size(iter,2),1),qHome(3).*ones(size(iter,2),1),qHome(4).*ones(size(iter,2),1),qHome(5).*ones(size(iter,2),1),qHome(6).*ones(size(iter,2),1)];
traj_des_theta = thetalist;
traj_des_XYZeul = geteul(traj_des_theta);
%test
Janaold = double(subs(Janasym,q_vec,thetalist(1,:)'));
[Xdd, Xd, X] = getDesiredX(thetalist(2,:)',dthetalist(2,:)',ddthetalist(2,:)',Janaold);
Janaold_e = double(subs(Janasym, q_vec, thetalist(1,:)'));
%% Initialize parameters for iterations
% Desired Mass of end effector
Md = 1*eye(6);
% Desired spring of end effector
Kp = 5*eye(6);
% Desired Damping coefficient of end effector
Kd = 3*eye(6);
% End effector initial force vector
he = [0 0 0 0 0 0]';
% Initial end effector actual cartesian position
xe = [THome(1:3,4);phi;theta;xi];
% Initial end effector desired cartesian acceleration. ddx = dJ_ana * dq + J_ana * ddq
xddoubled = [0 0 0 0 0 0]';
% Initial end effector desired cartesian velocity.dx = J_ana * dq
xddot = [0 0 0 0 0 0]';
% Initial end effector actual cartesian velocity
xedot = [subs(Pdot,[q_vec,qdot_vec],[qnew,qdotnew]);0;0;0];
% Initial difference in end effector desired and actual cartesian velocities
xtildedot = xddot - xedot;
%% Pre-allocating size of matrices for simulation iterations
save('vars_for_cb','iter','M','C','G','R0tip','Janasym','Janadot','Jgeom','Md','Kp','Kd','P_fin','q_vec','qdot_vec','xe','xddoubled','xtildedot','j','qnew','qdotnew','g','omega','euldot_old','Pdot','xddot','J','Janaold_e','dt');
% F_ext =1.* [5,-6,5,0,0,0].';
F_ext =2.* [2,-4,-3,0,0,0].';
% F_ext =1.* [0,0,0,0,0,0].';
[F,xehist,q_record,dq_record,ddq_record] = control_law(F_ext,traj_des_XYZeul,thetalist,dthetalist,ddthetalist);
figure(1)
subplot(2,1,1);
plot(F,'DisplayName','F','LineWidth',1.2)
ylabel('F');
xlabel('time');
title('F(ext)');
subplot(2,1,2);
plot(q_record,'DisplayName','q_record','LineWidth',1.2);
ylabel('theta');
xlabel('time');
title('theta');
figure(2)
subplot(2,1,1);
plot(F,'DisplayName','F','LineWidth',1.2)
ylabel('F');
xlabel('time');
title('F(ext)');
subplot(2,1,2);
plot(xehist,'DisplayName','xehist','LineWidth',1.2)
ylabel('X');
xlabel('time');
title('X');
figure(3)
subplot(2,1,1);
plot(q_record-thetalist,'DisplayName','xehist','LineWidth',1.2)
subplot(2,1,2);
plot(xehist-traj_des_XYZeul,'DisplayName','xehist','LineWidth',1.2)
% figure(4);
% plot3(traj_des_XYZeul(1:end,1),traj_des_XYZeul(1:end,2),traj_des_XYZeul(1:end,3),'b');
% for i = 1 : size(xehist,1)
% hold on
% plot3(xehist(i,1),xehist(i,2),xehist(i,3),'-o','Color','r','MarkerSize',10,'MarkerFaceColor','#D9FFFF');
% pause(0.001);
% end
figure(5);
plot3(traj_des_XYZeul(1:end,1),traj_des_XYZeul(1:end,2),traj_des_XYZeul(1:end,3),'b');
hold on
plot3(xehist(1:end,1),xehist(1:end,2),xehist(1:end,3),'Color','r');
figure(4);
plot3(traj_des_XYZeul(1:end,1),traj_des_XYZeul(1:end,2),traj_des_XYZeul(1:end,3),'b');
n = size(xehist,1) / 10;
for i = 1 : n
hold on
plot3(xehist(10 * i,1),xehist(10 * i,2),xehist(10 * i,3),'-o','Color','r','MarkerSize',10,'MarkerFaceColor','#D9FFFF');
pause(0.001);
end
链接:https://pan.baidu.com/s/1qvQDyDQ4koxEkMiqQWy5ig
提取码:z2le