LeetCode·每日一题·1851. 包含每个查询的最小区间·优先队列(小顶堆)
题目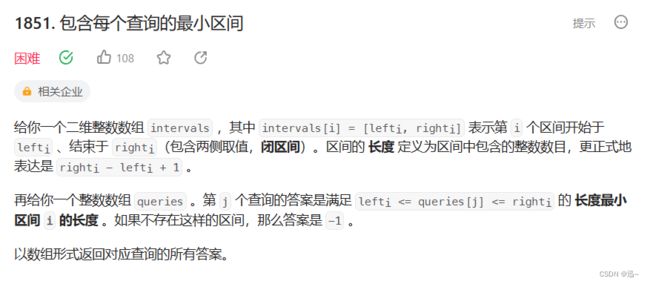
示例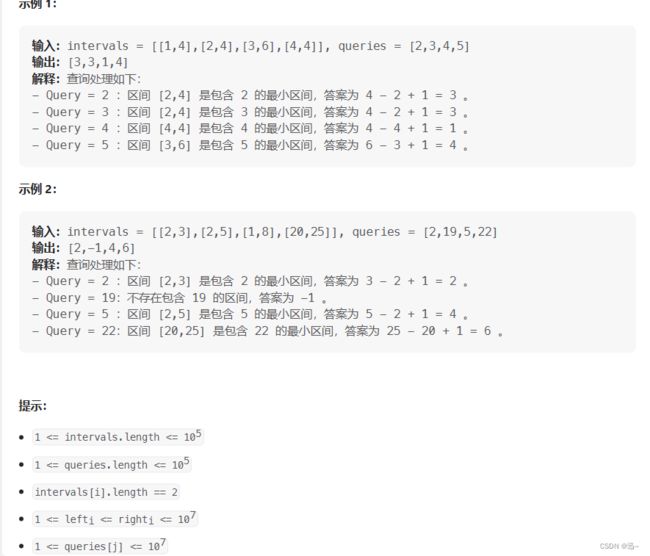
思路
- 离线查询:
- 输入的结果数组queries[]是无序的。如果我们按照输入的queries[]本身的顺序逐个查看,时间复杂度会比较高。 于是,我们将queries[]数组按照数值大小,由小到大逐个查询,这种方法称之为离线查询。
- 位运算:
- 离线查询的时候,queries[]可以按照数值大小逐个查看,但最终返回的结果数组,是需要按照queries[]相同的顺序输出的,也就是说,queries[]数组的下标信息不能被丢失。 此时,我们可以考虑,将每一个queries[x]放在一个long int数值的高32位,将下标x放在这个long int数值的低32位。 由此,我们可以看出,这些新的long int数值,它们之间的相互大小关系,取决于高32位的数值,只有在高32位相等的时候,才需要比较低32位。如此,我们在比较大小时,优先看高32位,然后想要获取其下标信息时,直接取低32位。 类似的,我们在处理输入的intervals[]数组时也类似处理。将每一个intervals[x]的左边缘放在一个long int数值的高32位,右边缘放在这个long int数值的低32位。这样,这些long int数值,它们之间的相互大小关系,就取决于左边缘的大小关系,而想要获取右边缘时,直接取低32位即可。
- 小根堆(优先队列):
- 我们要由小到大处理queries[]数组和intervals[]数组,可以考虑排序,也可以考虑小根堆,这里采用小根堆。
【具体实现】
- 将输入的intervals[]数组,每一个intervals[x]的左边缘放在一个long int数值的高32位,右边缘放在这个long int数组的低32位,然后long int数值push入小根堆intervalsHeap。
- 将输入的queries[]数组,每一个queries[x]的数值放在一个long int数值的高32位,下标x放在这个long int数值的低32位,然后long int数值push入小根堆queriesHeap。
- 逐个从queriesHeap中pop出堆顶元素,这个堆顶元素的高32位就是上面第2步push入堆时,每一个queries[x]的数值,赋值给变量position,低32位就是下标x。
- 3.1 从intervalsHeap中pop出所有左边缘(高32位)小于等于position的区间。
- 3.2 上面3.1中pop出的每一个区间,把所有右边缘(低32位)大于等于position的区间,都push入一个有效区间小根堆validHeap中。这个validHeap中,以区间的range为高32位,右边缘为低32位,以保证堆顶的区间range始终是最小的。
- 3.3 如果validHeap堆顶区间的右边缘(低32位)小于当前的position,则将其弹出。
- 3.4 经过上面3.3的操作后,如果validHeap仍然非空,则说明存在包含这个position的区间,且validHeap的堆顶区间的range(高32位)就是题目要求的结果。
代码
/* 几个全局定义的说明。
INVALID_VALUE: 无效值-1。小根堆中,根节点的父节点使用这个无效值。题目中结果数组里的无效值也是这个-1。
FATHER_NODE(x): 小根堆中,每一个节点的父节点。其中,根节点的父节点是无效值。
LEFT_NODE(x): 小根堆中,每一个节点的左子节点。当它大于等于堆size的时候无效。
RIGHT_NODE(x): 小根堆中,每一个节点的右子节点。当它大于等于堆size的时候无效。
MERGE_LONG(x, y): 两个int数值合并成一个long int数值,其中x占据高32位,y占据低32位。
GET_HIGHER32(x): 获取一个long int数值的高32位值。
GET_LOWER32(x): 获取一个long int数值的低32位值。 */
#define INVALID_VALUE -1
#define FATHER_NODE(x) ((0 == (x)) ? INVALID_VALUE : ((x) - 1 >> 1))
#define LEFT_NODE(x) (((x) << 1) + 1)
#define RIGHT_NODE(x) (((x) << 1) + 2)
#define MERGE_LONG(x, y) ((long int)(x) << 32 | (long int)(y))
#define GET_HIGHER32(x) ((x) >> 32)
#define GET_LOWER32(x) ((x) & 0xFFFFFFFF)
/* 小根堆的结构定义,里面包括堆空间数组arr[],和堆size。 */
typedef struct
{
long int *arr;
int arrSize;
}
HeapStruct;
static void heapPush(HeapStruct *heap, long int t);
static void heapPop(HeapStruct *heap);
/* 主函数的几个变量说明:
x: 循环下标。
position: queries数组中的数值。因为这个数组会带着下标一起入堆,在出堆时,把它的实际数值取出到这个position。
range: 题目中定义的一个左闭右闭区间的大小,等于“右边缘 - 左边缘 + 1”。
t: long int临时数值。
arr1,arr2,arr3: 几个小根堆中要用到的堆空间数组。
intervalsHeap: 将输入的intervals数组加入到这个小根堆中,左边缘放高32位,右边缘放低32位。
queriesHeap: 将输入的queries数组加入到这个小根堆中,数值放高32位,下标放低32位。
validHeap: 包含着当前position的有效区间的小根堆,区间range放高32位,右边缘放低32位。 */
int *minInterval(int **intervals, int intervalsSize, int *intervalsColSize, int *queries, int queriesSize, int *returnSize)
{
int x = 0, position = 0, range = 0;
long int t = 0;
long int arr1[intervalsSize], arr2[queriesSize], arr3[intervalsSize];
HeapStruct intervalsHeap, queriesHeap, validHeap;
int *result = NULL;
/* 申请结果数组的内存空间。 */
result = (int *)malloc(sizeof(int) * queriesSize);
if(NULL == result)
{
*returnSize = 0;
return result;
}
/* 堆空间定义,初始化一开始堆都为空。 */
intervalsHeap.arr = arr1;
intervalsHeap.arrSize = 0;
queriesHeap.arr = arr2;
queriesHeap.arrSize = 0;
validHeap.arr = arr3;
validHeap.arrSize = 0;
/* 把所有的区间放入堆中,左边缘为高优先级,右边缘为低优先级。 */
while(intervalsSize > x)
{
t = MERGE_LONG(intervals[x][0], intervals[x][1]);
heapPush(&intervalsHeap, t);
x++;
}
/* 把所有的查询放入堆中,位置为高优先级,下标为低优先级。 */
x = 0;
while(queriesSize > x)
{
t = MERGE_LONG(queries[x], x);
heapPush(&queriesHeap, t);
x++;
}
/* 一个个查询逐个出堆。 */
while(0 < queriesHeap.arrSize)
{
/* 把下标和位置列出,然后出堆。 */
x = GET_LOWER32(queriesHeap.arr[0]);
position = GET_HIGHER32(queriesHeap.arr[0]);
heapPop(&queriesHeap);
/* 把所有左边缘小于等于position的区间弹出。 */
while(0 < intervalsHeap.arrSize && position >= GET_HIGHER32(intervalsHeap.arr[0]))
{
/* 右边缘大于等于position的区间放到有效堆中(右边缘小于position的不可能包含当前position)。
这个有效堆以range为第一优先级,确保堆顶的区间是range最小的。 */
if(position <= GET_LOWER32(intervalsHeap.arr[0]))
{
range = GET_LOWER32(intervalsHeap.arr[0]) - GET_HIGHER32(intervalsHeap.arr[0]) + 1;
t = MERGE_LONG(range, GET_LOWER32(intervalsHeap.arr[0]));
heapPush(&validHeap, t);
}
heapPop(&intervalsHeap);
}
/* 有效堆中,如果堆顶的右边缘小于position,则弹出。这里用到了延迟删除的思想。因为最小堆的pop操作只能针对堆顶。
上面对validHeap进行push操作之后,堆顶的区间右边缘值可能已经小于当前的位置了,这种情况必须pop出去。 */
while(0 < validHeap.arrSize && position > GET_LOWER32(validHeap.arr[0]))
{
heapPop(&validHeap);
}
/* 如果此时的有效堆非空,则当前查询的取值就是堆顶的区间大小,否则就是题目要求的-1。 */
result[x] = (0 < validHeap.arrSize) ? GET_HIGHER32(validHeap.arr[0]) : INVALID_VALUE;
}
/* 返回数组长度等于queriesSize。 */
*returnSize = queriesSize;
return result;
}
/* 小根堆的push操作。
为确保其保持为一棵完整二叉树,新push入的数值初始放到堆尾,然后,根据父子节点的大小关系调整位置。 */
static void heapPush(HeapStruct *heap, long int t)
{
int son = heap->arrSize, father = FATHER_NODE(son);
heap->arrSize++;
while(INVALID_VALUE != father && heap->arr[father] > t)
{
heap->arr[son] = heap->arr[father];
son = father;
father = FATHER_NODE(son);
}
heap->arr[son] = t;
return;
}
/* 小根堆的pop操作。
堆顶弹出后,堆顶空缺,为确保其保持为一棵完整二叉树,将堆尾的数值补充到堆顶,然后,根据父子节点的大小关系调整位置。 */
static void heapPop(HeapStruct *heap)
{
int father = 0, left = LEFT_NODE(father), right = RIGHT_NODE(father), son = 0;
long int t = heap->arr[heap->arrSize - 1];
heap->arrSize--;
while((heap->arrSize > left && heap->arr[left] < t)
|| (heap->arrSize > right && heap->arr[right] < t))
{
son = (heap->arrSize > right && heap->arr[right] < heap->arr[left]) ? right : left;
heap->arr[father] = heap->arr[son];
father = son;
left = LEFT_NODE(father);
right = RIGHT_NODE(father);
}
heap->arr[father] = t;
return;
}
作者:恒等式
链接:https://leetcode.cn/problems/minimum-interval-to-include-each-query/solutions/2026632/bao-han-mei-ge-cha-xun-de-zui-xiao-qu-ji-lxkj/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。/* 几个全局定义的说明。
INVALID_VALUE: 无效值-1。小根堆中,根节点的父节点使用这个无效值。题目中结果数组里的无效值也是这个-1。
FATHER_NODE(x): 小根堆中,每一个节点的父节点。其中,根节点的父节点是无效值。
LEFT_NODE(x): 小根堆中,每一个节点的左子节点。当它大于等于堆size的时候无效。
RIGHT_NODE(x): 小根堆中,每一个节点的右子节点。当它大于等于堆size的时候无效。
MERGE_LONG(x, y): 两个int数值合并成一个long int数值,其中x占据高32位,y占据低32位。
GET_HIGHER32(x): 获取一个long int数值的高32位值。
GET_LOWER32(x): 获取一个long int数值的低32位值。 */
#define INVALID_VALUE -1
#define FATHER_NODE(x) ((0 == (x)) ? INVALID_VALUE : ((x) - 1 >> 1))
#define LEFT_NODE(x) (((x) << 1) + 1)
#define RIGHT_NODE(x) (((x) << 1) + 2)
#define MERGE_LONG(x, y) ((long int)(x) << 32 | (long int)(y))
#define GET_HIGHER32(x) ((x) >> 32)
#define GET_LOWER32(x) ((x) & 0xFFFFFFFF)
/* 小根堆的结构定义,里面包括堆空间数组arr[],和堆size。 */
typedef struct
{
long int *arr;
int arrSize;
}
HeapStruct;
static void heapPush(HeapStruct *heap, long int t);
static void heapPop(HeapStruct *heap);
/* 主函数的几个变量说明:
x: 循环下标。
position: queries数组中的数值。因为这个数组会带着下标一起入堆,在出堆时,把它的实际数值取出到这个position。
range: 题目中定义的一个左闭右闭区间的大小,等于“右边缘 - 左边缘 + 1”。
t: long int临时数值。
arr1,arr2,arr3: 几个小根堆中要用到的堆空间数组。
intervalsHeap: 将输入的intervals数组加入到这个小根堆中,左边缘放高32位,右边缘放低32位。
queriesHeap: 将输入的queries数组加入到这个小根堆中,数值放高32位,下标放低32位。
validHeap: 包含着当前position的有效区间的小根堆,区间range放高32位,右边缘放低32位。 */
int *minInterval(int **intervals, int intervalsSize, int *intervalsColSize, int *queries, int queriesSize, int *returnSize)
{
int x = 0, position = 0, range = 0;
long int t = 0;
long int arr1[intervalsSize], arr2[queriesSize], arr3[intervalsSize];
HeapStruct intervalsHeap, queriesHeap, validHeap;
int *result = NULL;
/* 申请结果数组的内存空间。 */
result = (int *)malloc(sizeof(int) * queriesSize);
if(NULL == result)
{
*returnSize = 0;
return result;
}
/* 堆空间定义,初始化一开始堆都为空。 */
intervalsHeap.arr = arr1;
intervalsHeap.arrSize = 0;
queriesHeap.arr = arr2;
queriesHeap.arrSize = 0;
validHeap.arr = arr3;
validHeap.arrSize = 0;
/* 把所有的区间放入堆中,左边缘为高优先级,右边缘为低优先级。 */
while(intervalsSize > x)
{
t = MERGE_LONG(intervals[x][0], intervals[x][1]);
heapPush(&intervalsHeap, t);
x++;
}
/* 把所有的查询放入堆中,位置为高优先级,下标为低优先级。 */
x = 0;
while(queriesSize > x)
{
t = MERGE_LONG(queries[x], x);
heapPush(&queriesHeap, t);
x++;
}
/* 一个个查询逐个出堆。 */
while(0 < queriesHeap.arrSize)
{
/* 把下标和位置列出,然后出堆。 */
x = GET_LOWER32(queriesHeap.arr[0]);
position = GET_HIGHER32(queriesHeap.arr[0]);
heapPop(&queriesHeap);
/* 把所有左边缘小于等于position的区间弹出。 */
while(0 < intervalsHeap.arrSize && position >= GET_HIGHER32(intervalsHeap.arr[0]))
{
/* 右边缘大于等于position的区间放到有效堆中(右边缘小于position的不可能包含当前position)。
这个有效堆以range为第一优先级,确保堆顶的区间是range最小的。 */
if(position <= GET_LOWER32(intervalsHeap.arr[0]))
{
range = GET_LOWER32(intervalsHeap.arr[0]) - GET_HIGHER32(intervalsHeap.arr[0]) + 1;
t = MERGE_LONG(range, GET_LOWER32(intervalsHeap.arr[0]));
heapPush(&validHeap, t);
}
heapPop(&intervalsHeap);
}
/* 有效堆中,如果堆顶的右边缘小于position,则弹出。这里用到了延迟删除的思想。因为最小堆的pop操作只能针对堆顶。
上面对validHeap进行push操作之后,堆顶的区间右边缘值可能已经小于当前的位置了,这种情况必须pop出去。 */
while(0 < validHeap.arrSize && position > GET_LOWER32(validHeap.arr[0]))
{
heapPop(&validHeap);
}
/* 如果此时的有效堆非空,则当前查询的取值就是堆顶的区间大小,否则就是题目要求的-1。 */
result[x] = (0 < validHeap.arrSize) ? GET_HIGHER32(validHeap.arr[0]) : INVALID_VALUE;
}
/* 返回数组长度等于queriesSize。 */
*returnSize = queriesSize;
return result;
}
/* 小根堆的push操作。
为确保其保持为一棵完整二叉树,新push入的数值初始放到堆尾,然后,根据父子节点的大小关系调整位置。 */
static void heapPush(HeapStruct *heap, long int t)
{
int son = heap->arrSize, father = FATHER_NODE(son);
heap->arrSize++;
while(INVALID_VALUE != father && heap->arr[father] > t)
{
heap->arr[son] = heap->arr[father];
son = father;
father = FATHER_NODE(son);
}
heap->arr[son] = t;
return;
}
/* 小根堆的pop操作。
堆顶弹出后,堆顶空缺,为确保其保持为一棵完整二叉树,将堆尾的数值补充到堆顶,然后,根据父子节点的大小关系调整位置。 */
static void heapPop(HeapStruct *heap)
{
int father = 0, left = LEFT_NODE(father), right = RIGHT_NODE(father), son = 0;
long int t = heap->arr[heap->arrSize - 1];
heap->arrSize--;
while((heap->arrSize > left && heap->arr[left] < t)
|| (heap->arrSize > right && heap->arr[right] < t))
{
son = (heap->arrSize > right && heap->arr[right] < heap->arr[left]) ? right : left;
heap->arr[father] = heap->arr[son];
father = son;
left = LEFT_NODE(father);
right = RIGHT_NODE(father);
}
heap->arr[father] = t;
return;
}