用图搜索方法求解迷宫问题

实验目的：深入掌握图遍历算法在求解实际问题中的应用
实验要求：
编写一个程序，完成以下功能。
（1） 建立一个迷宫对应的邻接表表示。
（2） 采用深度优先便利算法输出从入口（1，1）到出口（M，N）的所有迷宫路径。
（3） 采用广度优先便利算法输出从入口（1，1）到出口（M，N）的最短路径。
（4） 采用深度优先便利算法输出从入口（1，1）到出口（M，N）的所有最短路径。
迷宫如下图所示：

实验时间：6学时
实验地点：知行楼306
实验内容及结果：
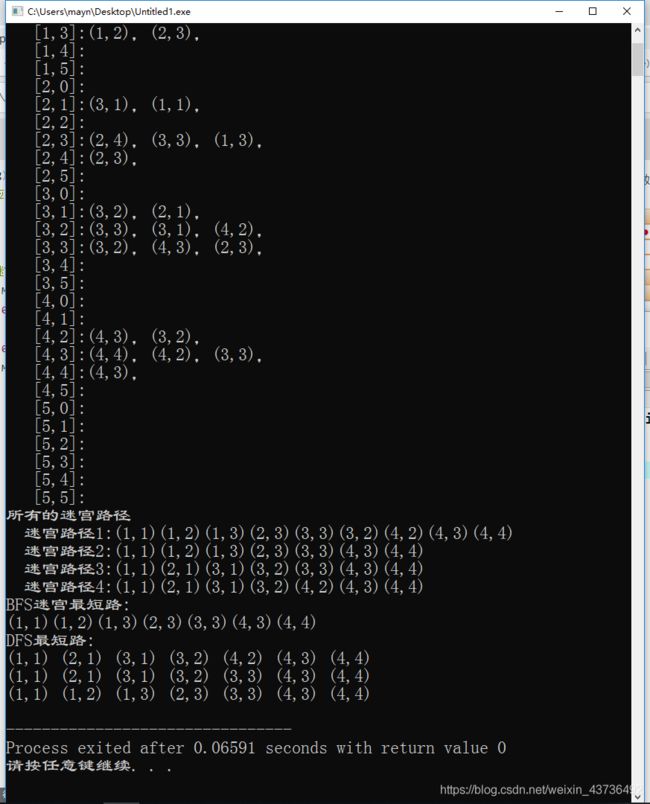
1、实现迷宫对应的邻接表表示。
2、实现采用深度优先便利算法输出从入口（1，1）到出口（M，N）的所有路径。
3、实现采用广度优先便利算法输出从入口（1，1）到出口（M，N）的最短路径。
4、实现采用深度优先遍历算法输出从入口（1，1）到出口（M，N）的所有最短路径。

Solution：

// Project37.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//
#include
#include
#include
#include
#define Maxsize 500
#define M 4
#define N 4
typedef struct ANode {
	int i, j;
	struct ANode *nextarc;
}ArcNode;
typedef struct Vnode {
	ArcNode *firstarc;
}VNode;
typedef struct {
	VNode adjlist[M + 2][N + 2];
}ALGraph;
typedef struct {
	int i, j;
}Box;
typedef struct {
	Box data[Maxsize];
	int length;
}Pathtype;
typedef struct list{
	int front,rear;
	Box data[Maxsize];
	list(){
		front=rear=-1;
	}
	bool Isempty(){
		return front==rear;
	}
	void Push(Box x){
		data[++rear]=x;
	}
	Box Front(){
		return data[++front];
	}
}Queue;
int visited[M + 2][N + 2] = { 0 };
int count = 0;
int dir[][2] = { {-1,0},{1,0},{0,-1},{0,1} };
void CreateAdj(ALGraph *&G, int mg[][N + 2]) {
	G = (ALGraph *)malloc(sizeof(ALGraph));
	for (int i = 0; i < M + 2; i++) {//初始化每个点的坐标对应的邻接表都是空
		for (int j = 0; j < N + 2; j++) {
			G->adjlist[i][j].firstarc = NULL;
		}
	}
	for (int i = 1; i <= M; i++) {
		for (int j = 0; j <= N; j++) {
			if (!mg[i][j]) {//mg[i][j]=0表示这个格子是可走的
				for (int k = 0; k < 4; k++) {//扫描这个格子对应的四个方向
					int fx = dir[k][0] + i;//当前点伸展出来的上下左右四个点的x坐标
					int fy = dir[k][1] + j; //当前点伸展出来的上下左右四个点的y坐标
					if (!mg[fx][fy]) {//mg[i][j]的某个方向的坐标mg[fx][fy]=0表示是可以走的我们就建立邻接表
						ArcNode *p = (ArcNode *)malloc(sizeof(ArcNode));
						p->i = fx; p->j = fy;//mg[i][j]的邻接表是mg[fx][fy]其中mg[fx][gy]=0并且是mg[i][j]的四个方向其中之一
						p->nextarc = G->adjlist[i][j].firstarc;//头插法建表
						G->adjlist[i][j].firstarc = p;
					}
				}
			}
		}
	}
}
void DisAdj(ALGraph *G) {
	for (int i = 0; i < M + 2; i++) {
		for (int j = 0; j < N + 2; j++) {
			printf("   [%d,%d]:", i, j);
			ArcNode *p = G->adjlist[i][j].firstarc;
			while (p != NULL) {
				printf("(%d,%d)，", p->i, p->j);
				p = p->nextarc;
			}
			puts("");
		}
	}
}
void destoryadj(ALGraph *G){
	ArcNode *pre,*p;
	for(int i = 0;i < M + 2; i++){
		for(int j = 0;j < N + 2; j++){
			pre=G->adjlist[i][j].firstarc;
			if(pre!=NULL){
				p=pre->nextarc;
				while(p!=NULL){
					free(pre);
					pre=p;p=p->nextarc;
				}
				free(pre);
			}
		}
	}
}

void FindPath(ALGraph *G,int x1,int y1,int x2,int y2,Pathtype path){//(x1,y1),(x2,y2)起点，终点
	visited[x1][y1]=1;//标记一下，说明当前这个点已经被访问
	path.data[path.length].i=x1;//把当前点x坐标存到路径中
	path.data[path.length++].j=y1; //把当前点y坐标存到路径中
	if(x1==x2&&y1==y2){//起点终点相等说明找到一条路径
		printf("  迷宫路径%d:",++count);
		for(int k=0;k<path.length;k++){//输出路径
			printf("(%d,%d)",path.data[k].i,path.data[k].j);
		}
		puts("");
	}
	ArcNode *p=G->adjlist[x1][y1].firstarc;//找到当前点的邻接表
	while(p!=NULL){//遍历当前点的邻接表
		if(!visited[p->i][p->j])//以及访问过的不再访问，避免死循环
		FindPath(G,p->i,p->j,x2,y2,path);//递归下一个点的邻接表
		p=p->nextarc;
	}
	visited[x1][y1]=0;//因为路有多条，每次遍历完一个点把他的状态修改一下
	
}
void bfs(ALGraph *G,int x1,int y1,int x2,int y2){
	Queue ans;//自定义了一个简单的容器队列 
	Box t={x1,y1};//设置t为入口坐标并且初始化 
	visited[t.i][t.j]=1;//设置入口坐标已经被访问 
	ans.Push(t);//入口坐标入队 
	Box path[Maxsize][Maxsize];//Box二维数组存路径 Box[i][j]=Box{p,q}表示迷宫坐标(i,j)的父亲节点是(p,q),也就是(i,j)的上一步坐标是(p,q) 
	while(!ans.Isempty()){//队列不空 
		Box now=ans.Front();//出队列一个元素 
		if(now.i==x2&&now.j==y2){//找到终点 
			printf("BFS迷宫最短路:\n");
			Box ans[100];int cnt=1;
			ans[0].i=x2;ans[0].j=y2;
			while(x2!=x1||y2!=y1){//通过循环不断的找它的父亲节点也就是它的上一步是什么一直逆推到起点坐标就结束，然后把这条路径存在数组ans[i]中 
				int t1=path[x2][y2].i;
				int t2=path[x2][y2].j;
				ans[cnt].i=t1;ans[cnt++].j=t2;
				x2=t1;y2=t2;
			}
			for(int i=cnt-1;i>=0;i--){//输出这条路径 
				printf("(%d,%d)",ans[i].i,ans[i].j);
			}
			puts("");
			break;
		}
		ArcNode *p=G->adjlist[now.i][now.j].firstarc;//找到当前点的邻接表
		while(p!=NULL){//遍历邻接表 
			if(!visited[p->i][p->j]){//访问过的点不再访问 
				visited[p->i][p->j]=1;//设置该点已访问 
				Box cur={p->i,p->j};//取出该点坐标 
				ans.Push(cur);//如果 
				path[p->i][p->j]=now;//记录该点的上一步坐标 
			}
			p=p->nextarc;//继续遍历 
		}
	} 
}
Pathtype Path[100];int shortpath=9999;int cnt=0;
void shortdfs(ALGraph *G,int x1,int y1,int x2,int y2,Pathtype path){
	visited[x1][y1]=1;//标记一下，说明当前这个点已经被访问
	path.data[path.length].i=x1;//把当前点x坐标存到路径中
	path.data[path.length++].j=y1; //把当前点y坐标存到路径中
	if(x1==x2&&y1==y2){//起点终点相等说明找到一条路径
		shortpath=std::min(shortpath,path.length);
		Path[++cnt]=path;
	}
	ArcNode *p=G->adjlist[x1][y1].firstarc;//找到当前点的邻接表
	while(p!=NULL){//遍历当前点的邻接表
		if(!visited[p->i][p->j])//以及访问过的不再访问，避免死循环
		shortdfs(G,p->i,p->j,x2,y2,path);//递归下一个点的邻接表
		p=p->nextarc;
	}
	visited[x1][y1]=0;//因为路有多条，每次遍历完一个点把他的状态修改一下-
}
void display(){
	printf("DFS最短路:\n");
	for(int i=cnt;i>0;i--){
		if(Path[i].length==shortpath){
			for(int j=0;j<Path[i].length;j++){
				printf("(%d,%d) ",Path[i].data[j].i,Path[i].data[j].j);
			}
			puts("");
		} 
	}
}
int main() {
	ALGraph *G;
	int mg[M + 2][N + 2] = { {1,1,1,1,1,1},
	{1,0,0,0,1,1},
	{1,0,1,0,0,1},
	{1,0,0,0,1,1},
	{1,1,0,0,0,1},
	{1,1,1,1,1,1} };
	CreateAdj(G, mg);
	printf("迷宫对应的邻接表\n");
	DisAdj(G);
	Pathtype path;
	path.length=0;
	printf("所有的迷宫路径\n");
	FindPath(G,1,1,M,N,path);
	memset(visited,0,sizeof(visited));
	bfs(G,1,1,M,N);
	memset(visited,0,sizeof(visited));
	shortdfs(G,1,1,M,N,path); 
	display(); 
	destoryadj(G);
}