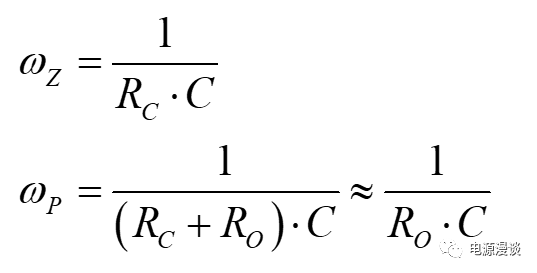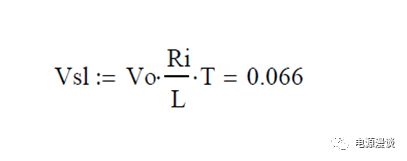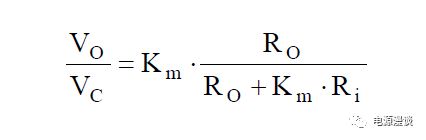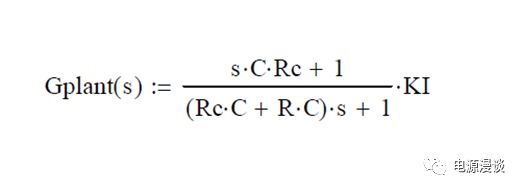峰值电流模式控制BUCK电路功率级电路计算及仿真
前述文章,BUCK功率级电路频域计算及仿真 ,讨论了电压模式BUCK电路的功率级电路计算及仿真,并进行了频域的闭环设计。由于峰值电流模式相比电压模式具有不少优点,所以应用也很广泛,本文就对峰值电流模式控制BUCK功率级电路做一些详细分析计算和仿真。
来源:电源漫谈 ,作者电源漫谈
一、峰值电流模式的基本运行原理
先回顾一下峰值电流模式BUCK电路的基本运行原理,其基本原理框图如图1所示。
图1 峰值电流模式BUCK基本电路框图
从图1的基本框图分析来看,在电压模式中的固定频率锯齿波,已经被电流采样电压波形所代替,它和电压控制环的输出误差去比较,以此产生占空比的下降沿信号,占空比的上升沿由一个固定频率的时钟所产生。基于以上分析,误差放大器输出并不是直接控制占空比,而是控制峰值电流,如图2所示,当电流峰值达到电压环输出后,占空比的下降沿就会产生。
图2 误差放大器输出控制峰值电流
二、峰值电流模式BUCK的频域简易模型
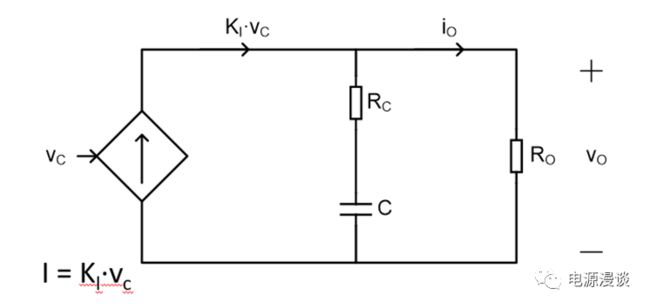
基于上述分析,峰值电流控制模式BUCK可以看作一个电压控制电流源,电感电流峰值由电压环误差输出决定,系数是电流环调制器增益,则基于这个模型很容易求得峰值电流模式的控制量Vc到输出电压Vo的频域传递函数。这里我们采用简易模型,假设电流环将LC二阶极点系统变为一阶极点系统,电感的作用在电流环的作用下消失了,这在直流和低频下来说是适用的。
图3 峰值电流控制模式Power Stage电压控制电流源模型
图4 BUCK电路峰值电流模式控制到输出的传递函数
由图4中的控制Vc到输出Vo简化传递函数来看,可以将其看作一个一阶环节,其直流增益为G0,具有一个零点和一个极点。由上述表达式来看,其零点决定于输出电容及其ESR电阻,其极点决定于输出电容及负载电阻,此时,相对于负载电阻来说ESR电阻非常小,也可以忽略ESR电阻。
图5 BUCK电路峰值电流控制模式的功率级电路零点和极点
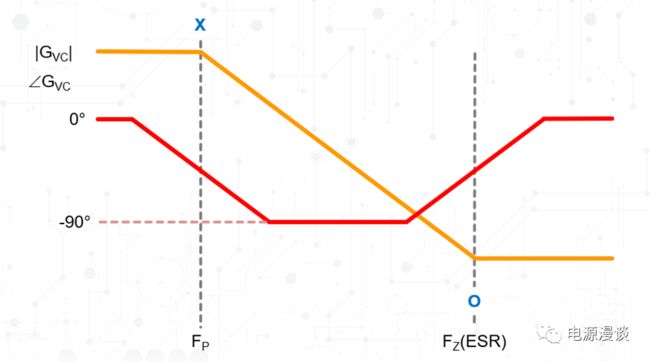
图6 BUCK电路峰值电流控制模式的功率级电路Bode图
由上述计算得到的零极点,我们画出功率级期望的Bode图,如图6所示,在低频段直流增益取决于G0,Fp极点处增益以-20db/10倍频斜率下掉,相应的相位产生90C的滞后,在输出电容ESR零点处,增益又产生20db/10倍频的斜率变化,所以变为一条水平线,相应的相位又回到0C找元器件现货上唯样商城.
三、BUCK电路峰值电流模式控制直流增益及功率级零极点计算
为了方便计算,定义BUCK电路功率级的相关参数,如下图7所示。
图7 功率级计算参数定义
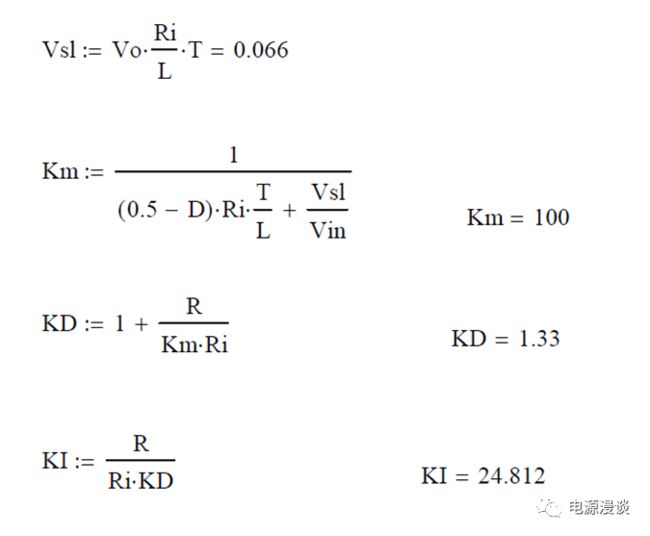
图7中,定义BUCK电路输入电压为9V,输出电压为3.3V,负载电阻为3.3ohm(对应负载电流为1A),输出电容为100uF,Rc为其ESR电阻,输出电感为10uH,RL为其寄生串联电阻ESL,Ri为电流采样的比例增益设为0.1。
峰值电流模式在占空比大于50%时,需要对采样电流波形增加斜坡补偿才能让环路稳定,否则会造成次谐波震荡,振荡频率为一半的开关频率。对于BUCK变换器来说,电流转化为电压后的上升沿的斜率为如下式定义,
而电流转化为电压后下降沿的斜率,由下式定义,
这里需要加的斜坡补偿量设为下降沿斜率,关于斜坡补偿的具体分析我们后面会详细讨论,这里先采用这一结论,计算得到整个周期的斜坡补偿电压为如下式,所示。
由于调制器的增益由输出电阻和电流环增益所分压,由此求得控制到输出的直流关系如下式所示。
根据斜波补偿的计算,以及PWM调制器的传递函数的概念,可计算上式中峰值电流模式的直流增益,如下图8,计算得知直流增益为27.8db。
图8 峰值电流模式控制到输出直流增益
图9 峰值电流模式BUCK控制到输出的传递函数
根据图3所示的电压控制电流源模型,我们可以推导出控制到输出的传递函数如图9所示,将s=0,则得知其直流增益为KI.同时,我们可以在此简化模型上得知功率级包含一个极点和一个零点,我们计算其转折频率如下图10所示。
图10 峰值电流模式BUCK零极点计算
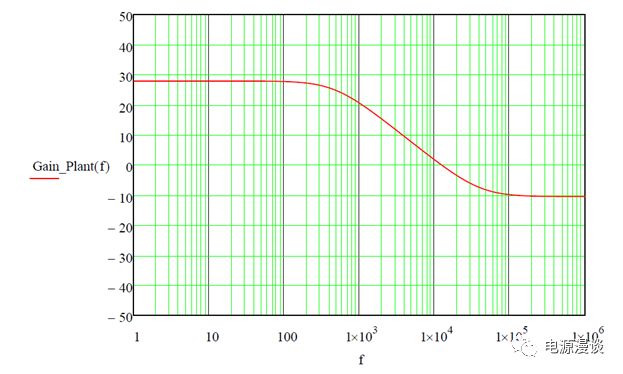
图11 峰值电流模式BUCK控制到输出增益曲线
从图11的控制到输出传递函数增益曲线上看,低频时是一个不到30db的直流增益,在大约500Hz附近,有一个极点使得增益曲线斜率为-20db/10倍频,在大约40k附近,出现一个零点,让增益曲线的斜率变回0db/10倍频。
图12 峰值电流模式BUCK控制到输出相位曲线
从图12相位曲线上看,对应于增益曲线,极点让相位滞后约90C,零点又让相位回到起始的0C,符合我们的上述分析。
图13 穿越频率/相位裕量/低频增益计算
在上述控制到输出的传递函数的相位及增益曲线上,很容易求得一些关键参数,如穿越频率,相位裕量,低频增益等,结果如图13所示,我们可知穿越频率为12.37k,相位裕量为110C,低频增益为27.9db。
图14 零极点处的相位和增益计算
在功率级传递函数的Bode图上,还可以求得零极点对应的增益和相位,如极点处相位滞后为-45C左右,零点处在极点10倍频时滞后的相位90C基础上,又提升了45C,所以零点处相位滞后还是为-45C,以上符合分析。
四、峰值电流模式BUCK电路功率级仿真验证
图15 峰值电流模式BUCK功率级时域及小信号仿真
在上图15中,给出了峰值电流模式BUCK电路的开环仿真原理图,非常简洁。参数设置和上述第三部分的计算一致。例如,输入电压9V,电压控制电流源的电压为142mv时,输出电压为3.3V,同时斜坡补偿在整个周期最大值为66mV,和上述计算一致。电流采样增益,按照Ri=0.1,采用电流控制电压源设置,其它参数也可以参考上述第三部分计算,此处不一一详述。
图16 峰值电流模式控制BUCK开环仿真波形1
在上面图16中,到的时域仿真波形自上到下分别为斜坡补偿后的电流采样电压V_CS,电压环给定V_COMP,开关节点电压SW,开关管下管驱动波形PWM1L。
图17 峰值电流模式控制BUCK开环仿真波形2
在上面图17中,得到的时域仿真波形2自上到下分别为开关管门级上管驱动波形PWM1H_mos,开关管上管驱动波形PWM1H,输入电流波形IVIN,续流二极管也就是死区电流波形ID1.
图18 峰值电流模式控制BUCK开环仿真波形3
在上面图18中,得到的时域仿真波形3自上到下分别为续流管mosfet的波形IS2,电感电流波形IL,输出电压波形VOUT.
根据以上开环仿真波形,可以判断基本上是我们期望的合理的开环电路波形。接下来,进行小信号环路仿真,事先在电路中放置了环路Bode图测试仪器,及在电压环输出施加了小信号干扰源。
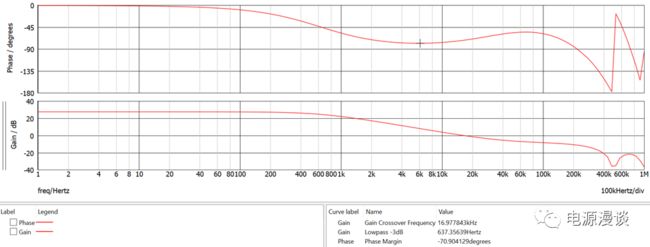
图19 峰值电流模式控制BUCK电路功率级Bode图
从图19小信号开环仿真结果来看,得到控制到输出的传递函数对应的Bode图,从图上看,穿越频率为16.97k,负载极点频率为637Hz,和理论计算有一些差异,可能源于计算负载极点的模型不够精确。
采用计算负载极点的非简化模型,即不忽略KD(此处KD为1.33)参数,如下图20所示计算,得知负载极点为641Hz,和仿真模型比较一致。由于传递函数模型简化,所以计算得到的穿越频率和实际仿真值相比稍低。
图20 未忽略KD时的负载极点频率计算
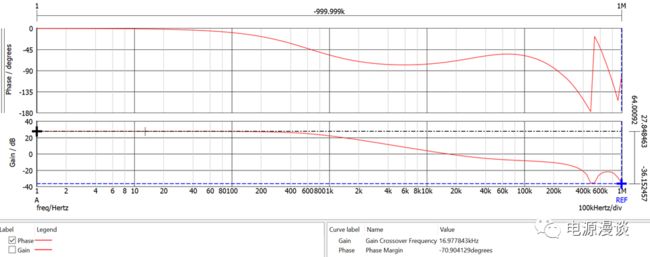
图21 峰值电流模式控制BUCK电路功率级低频增益测量
从图19测量增益曲线来看,低频增益为27.8db,和计算结果非常一致。从测试的相位来看,相位为70C,因此相位裕量为110C,和计算结果也很一致。
总结,本文通过分析峰值电流模式BUCK电路的功率级电路模型,计算了从控制到输出传递函数的一些非常重要的参数如直流增益,穿越频率,零极点频率等,并且通过仿真进行了验证,为后续峰值电流模式BUCK电路闭环补偿设计奠定基础。