leetcode-动态规划【背包问题】
背包问题篇:
基础背包:
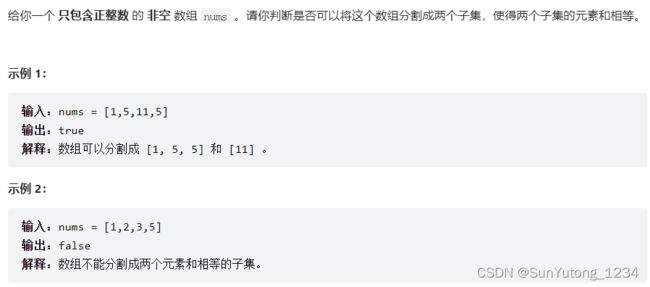
416. 分割等和子集
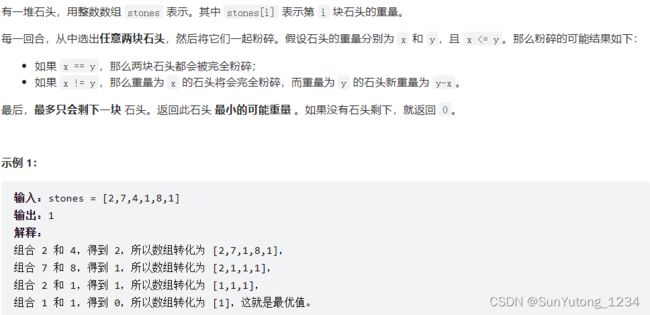
1049. 最后一块石头的重量ii
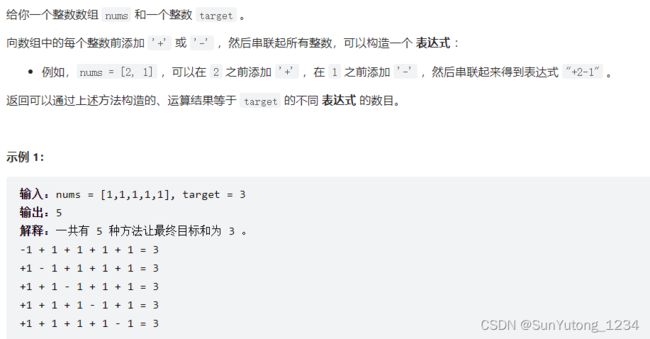
494. 目标和
474. 一和零
完全背包:
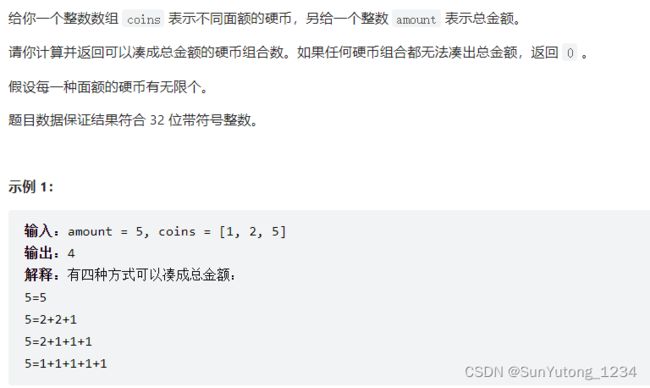
518. 零钱兑换ii
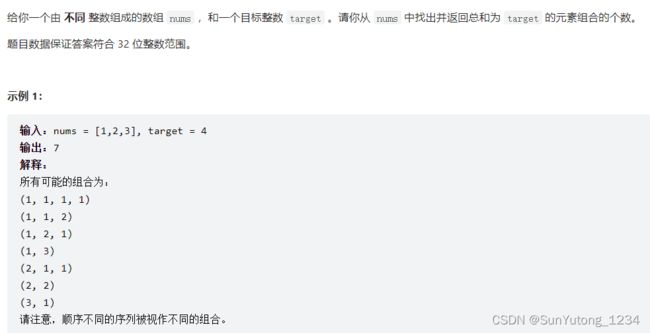
377. 组合总和iv
70. 爬楼梯
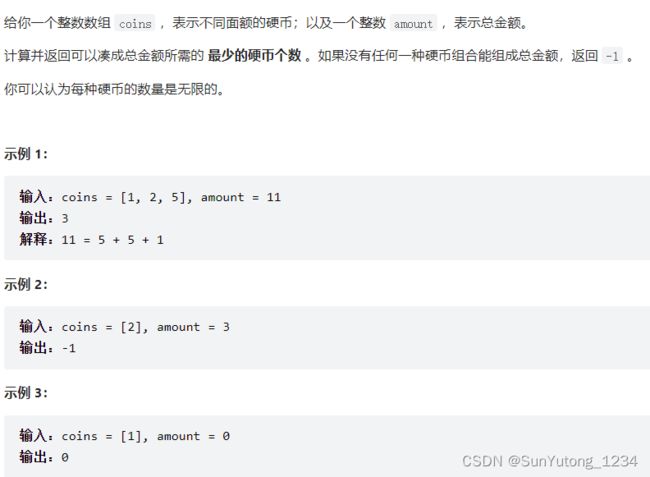
322. 零钱兑换
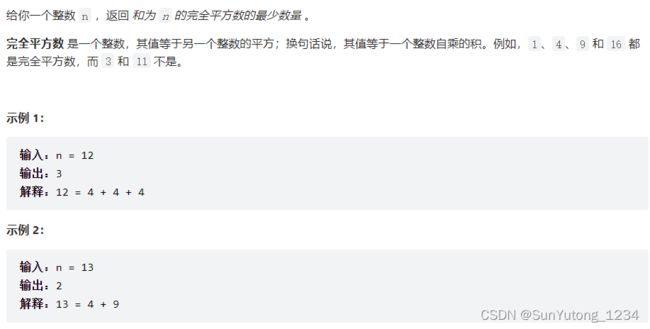
279. 完全平方数
139. 单词拆分
多重背包:
0-1背包:(所有元素只能放入一次)
n件物品和最大承受重量为w的背包,其中第i件物品的重量是weight[i],得到的价值是value[i],每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
1. 确定dp数组以及下标的含义
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。i:物品编号,j:背包容量,dp[i][j]:价值总和
2. 确定递推公式
- 不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以被背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
3. dp数组初始化
dp[i][0]:背包容量为0因此价值总和为0
dp[0][j]:存放物品0的时候背包价值总和,当j 4. 确定遍历顺序:先遍历物品/背包重量 5. 举例推导dp数组 使用滑动数组: 第二种方法: 假设nums = [3,1,2,5,4],此时选3和1前面的符号为加号,其余为减号,那么此时加法获得的和为3+1=4,减法获得的和为2+5+4=11,也可以通过sum(nums)-3-1=15-3-1=11获得。以此类推,设加法获得的和为x,则减法获得的和为(sum-x),问题转化满足x-(sum-x)=target / x=(sum+target)/2有几种方案。 dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。416. 分割等和子集
class Solution(object):
def canPartition(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
if sum(nums) % 2: return False
# 要求找到元素和为sum/2的子集
target = sum(nums) // 2
# dp[i][j]代表可装物品为0-i,背包容量为j的情况下,背包内容量的最大价值(最大子集和)
dp = [[0 for _ in range(target+1)] for _ in range(len(nums))]
# 背包容量为0且只能放入nums[i]的情况下背包最大价值(最大子集和)
for j in range(nums[0],target+1):
dp[0][j] = nums[0]
# 递推公式(每行从左到右遍历)
for i in range(1, len(nums)):
for j in range(1, target+1):
# 当背包不能容纳nums[i]时
if j < nums[i]:
dp[i][j] = dp[i-1][j]
# 当背包可以容纳nums[i]时
else:
dp[i][j] = max(dp[i-1][j], dp[i-1][j-nums[i]] + nums[i])
return dp[-1][-1] == targetclass Solution(object):
def canPartition(self, nums):
"""
:type nums: List[int]
:rtype: bool
"""
if not nums or sum(nums) % 2: return False
target = sum(nums) // 2
# 滑动数组(因为只需要保留上一行的值因此可以使用一维数组)
dp = [0 for _ in range(target+1)]
for i in range(len(nums)):
for j in range(target, nums[i]-1, -1):
dp[j] = max(dp[j], dp[j-nums[i]] + nums[i])
return dp[-1] == target1049. 最后一块石头的重量ii
class Solution(object):
def lastStoneWeightII(self, stones):
"""
:type stones: List[int]
:rtype: int
"""
# 将stones分为重量差不多的两堆
target = sum(stones) // 2
# dp设为滑动数组,dp[j]存储最接近重量j其不超过的石头总重量
dp = [0 for _ in range(target+1)]
# 遍历stones
for i in range(len(stones)):
for j in range(target, stones[i]-1, -1):
dp[j] = max(dp[j], dp[j-stones[i]]+stones[i])
return sum(stones)-2*dp[-1]494. 目标和
class Solution(object):
def findTargetSumWays(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
if len(nums) == 1 and nums[0] != target and nums[0] != -1 * target:
return 0
sum_nums = sum(nums)
if target > sum_nums or target < -1 * sum_nums: return 0
# dp[][sum_nums]为中心点
dp = [[0 for _ in range(2*sum_nums+1)] for _ in range(len(nums))]
for j in range(2*sum_nums+1):
if abs(j - sum_nums) == nums[0]:
if nums[0] == 0: dp[0][j] = 2
else: dp[0][j] = 1
for i in range(len(nums)-1):
for j in range(2*sum_nums+1):
if dp[i][j] == 0: continue
dp[i + 1][j - nums[i + 1]] += dp[i][j]
dp[i + 1][j + nums[i + 1]] += dp[i][j]
return dp[-1][target+sum_nums]class Solution(object):
def findTargetSumWays(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
sum_nums = sum(nums)
# 注意边界条件
if abs(target) > sum_nums or (sum_nums + target) % 2 == 1: return 0
bagSize = (sum_nums + target) // 2
dp = [0] * (bagSize + 1)
dp[0] = 1
for i in range(len(nums)):
for j in range(bagSize, nums[i] - 1, -1):
dp[j] += dp[j - nums[i]]
return dp[bagSize]474. 一和零
class Solution(object):
def findMaxForm(self, strs, m, n):
"""
:type strs: List[str]
:type m: int
:type n: int
:rtype: int
"""
# dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]
dp = [[0 for _ in range(n+1)] for _ in range(m+1)]
for str in strs:
onenum = str.count('1')
zeronum = str.count('0')
for i in range(m, zeronum-1, -1):
for j in range(n, onenum-1, -1):
dp[i][j] = max(dp[i][j], dp[i-zeronum][j-onenum] + 1)
return dp[m][n]完全背包:(元素可以重复放入)
518. 零钱兑换ii
class Solution(object):
def change(self, amount, coins):
"""
:type amount: int
:type coins: List[int]
:rtype: int
"""
# dp[i][j]表示coins[i]的面值加入排列后,总和为amount的组合数
dp = [0 for _ in range(amount+1)]
dp[0] = 1
for i in range(len(coins)):
for j in range(coins[i], amount+1):
dp[j] += dp[j-coins[i]]
return dp[-1]377. 组合总和iv
class Solution(object):
def combinationSum4(self, nums, target):
"""
:type nums: List[int]
:type target: int
:rtype: int
"""
dp = [0 for _ in range(target+1)]
dp[0] = 1
for j in range(target+1):
for i in range(len(nums)):
if j-nums[i] >= 0:
dp[j] += dp[j-nums[i]]
return dp[-1]70. 爬楼梯
class Solution(object):
def climbStairs(self, n):
"""
:type n: int
:rtype: int
"""
dp = [0 for _ in range(n+1)]
dp[0] = 1
for j in range(n+1):
for step in range(1,3):
if j - step >= 0:
dp[j] += dp[j-step]
return dp[-1]322. 零钱兑换
class Solution(object):
def coinChange(self, coins, amount):
"""
:type coins: List[int]
:type amount: int
:rtype: int
"""
dp = [amount + 1] * (amount + 1)
dp[0] = 0
for coin in coins:
for j in range(coin, amount + 1):
dp[j] = min(dp[j], dp[j - coin] + 1)
if dp[amount] < amount + 1:
return dp[amount]
else:
return -1279. 完全平方数
class Solution(object):
def numSquares(self, n):
"""
:type n: int
:rtype: int
"""
square, i = [], 1
while i**2 <= n:
square.append(i**2)
i += 1
dp = [n+1] * (n+1)
dp[0] = 0
for i in range(len(square)):
for j in range(square[i], n+1):
dp[j] = min(dp[j], dp[j-square[i]]+1)
if dp[n] > n+1:
return -1
else:
return dp[n]139. 单词拆分
class Solution(object):
def wordBreak(self, s, wordDict):
"""
:type s: str
:type wordDict: List[str]
:rtype: bool
"""
# dp[j]=1即截至此处s[:j+1]可划分,dp[j]=0即不可划分
dp = [0 for _ in range(len(s)+1)]
dp[0] = 1
for j in range(1, len(s)+1):
for word in wordDict:
if j >= len(word):
dp[j] = dp[j] or (dp[j - len(word)] and word == s[j - len(word):j])
return dp[-1] == 1多重背包: