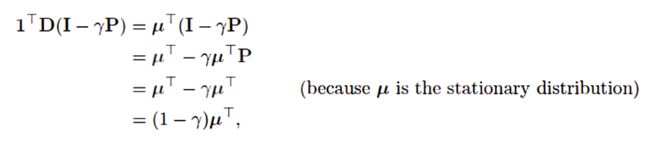强化学习(七) - 函数近似方法 - 随机梯度下降, 半梯度下降,及瓦片编码(Tile Coding)实例
函数近似方法
-
-
- 7.1 目标预测( V E ‾ \overline{VE} VE)
- 7.2 随机梯度下降和半梯度下降
-
- 例7.1: 1000态随机行走的状态收敛
- 7.3 线性近似
- 7.4 线性方法的特征构造
-
- 7.4.1 Coarse Coding(粗编码)
- 例7.2:粗编码的粗度
- 7.4.2 Tile Coding(瓦片编码)
- 7.4.3 实例:Tile Coding实例
-
- (1) 环境, 动作和状态空间
- (2) 瓦片化
- (3) 瓦片编码
- (4) 使用瓦片编码的Q表
- (5) Q学习智能体
- (6)模型训练
- (7)完整代码
-
本节介绍用函数近似(function approximation)方法来估计给定策略 π π π的状态价值函数 v π v_π vπ或动作价值函数 q π q_π qπ。要评估状态价值,我们可以用一个参数为 w \text{w} w的函数 v ( s ; w ) v(s;\text{w}) v(s;w)( s ∈ S s∈\mathcal{S} s∈S)来近似状态价值;要评估动作价值,我们可以用一个参数为 w \text{w} w的函数 q ( s , a ; w ) q(s,a;\text{w}) q(s,a;w)( s ∈ S s∈\mathcal{S} s∈S, a ∈ A ( s ) a∈\mathcal{A}(s) a∈A(s))来近似动作价值。在动作集 A \mathcal{A} A有限的情况下,还可以用一个矢量函数 q ( s ; w ) = ( q ( s , a ; w ) : a ∈ A q(s;\text{w})=(q(s,a;\text{w}):a∈\mathcal{A} q(s;w)=(q(s,a;w):a∈A)( s ∈ S s∈\mathcal{S} s∈S)来近似动作价值。矢量函数 q ( s ; w ) q(s;\text{w}) q(s;w)的每一个元素对应着一个动作,而整个矢量函数除参数外只用状态作为输入。这里的函数 v ( s ; w ) s ∈ S v(s;\text{w}) s∈\mathcal{S} v(s;w)s∈S)、 q ( s , a ; w ) q(s,a;\text{w}) q(s,a;w)( s ∈ S s∈\mathcal{S} s∈S, a ∈ A a∈\mathcal{A} a∈A(s))、 q ( s ; w ) ( s ∈ S ) q(s;\text{w})(s∈\mathcal{S}) q(s;w)(s∈S)形式不限,可以是线性函数,也可以是神经网络。但是,它们的形式需要事先给定,在学习过程中只更新参数 w \text{w} w。一旦参数 w \text{w} w完全确定,价值估计就完全给定。所以,本节将介绍如何更新参数 w \text{w} w。更新参数的方法既可以用于策略价值评估,也可以用于最优策略求解。
7.1 目标预测( V E ‾ \overline{VE} VE)
到目前为止,我们还没有为预测指定一个明确的目标。在使用表格的情况下,预测质量的连续测量是不必要的,因为学习的值函数可以完全等于真值函数。此外,每个状态下的学习值是解耦的,一个状态下的更新不会影响其他状态。但是在真正的近似中,一个状态的更新会影响到许多其他状态,而且不可能得到所有状态的值完全正确。根据假设,我们的状态比权重多得多,所以使一个状态的估计更准确必然意味着使其他状态的估计更不准确。那么我们有必要指出我们最关心的状态。我们必须指定一个状态分布 μ ( s ) ≥ 0 , ∑ s μ ( s ) = 1 μ(s) \geq 0,\sum_{s} μ(s) = 1 μ(s)≥0,∑sμ(s)=1,代表我们对每个状态 s s s的误差的关心程度,所谓状态 s s s的误差是指近似值 v ( s , w ) v(s,w) v(s,w)与真实值 v ( s ) v(s) v(s)之差的平方。将其在状态空间中的权重为 μ μ μ,我们得到一个自然的目标函数,即均值平方误差(Mean SquaredValue Error),表示为 V E ‾ \overline{VE} VE。
V E ‾ ( w ) ≐ ∑ s ∈ S μ ( s ) [ v π ( s ) − v ^ ( s , w ) ] 2 (7.1) \overline{VE}(w) \doteq \sum_{s\in\mathcal{S}}\mu(s)[v_\pi(s) - \hat{v}(s, w)]^2 \tag{7.1} VE(w)≐s∈S∑μ(s)[vπ(s)−v^(s,w)]2(7.1)
这个度量的平方根,即 V E ‾ \overline{VE} VE,可以粗略地衡量近似值与真实值的差距有多大,并且经常被用于绘图中。通常 μ ( s ) μ(s) μ(s)被选择为在 s s s中花费的时间分数。在on-policy的训练下,这被称为on-policy分布;我们在本章中完全关注这种情况。在连续性任务中,on-policy分布是在策略 π \pi π下的固定分布。
事件性任务中的on-policy分布
在事件性任务中,on-policy分布有点不同,它取决于如何选择事件的初始状态。让 h ( s ) h(s) h(s)表示一个事件开始于每个状态 s s s的概率,让 μ ( s ) \mu(s) μ(s)表示一个事件平均在状态 s s s中花费的时间步数。如果从 s s s开始,或者从前一个状态 s ˉ \bar{s} sˉ过渡到 s s s中,则花费在状态 s s s中时间为
μ ( s ) = h ( s ) + ∑ s ^ μ ( s ˉ ) ∑ a π ( a ∣ s ˉ ) p ( s ∣ s ˉ , a ) , for all s ∈ S (7.2) \mu(s) = h(s) + \sum_{\hat{s}}\mu(\bar{s})\sum_{a}\pi(a|\bar{s})p(s|\bar{s}, a), \text{for all } s \in \mathcal{S} \tag{7.2} μ(s)=h(s)+s^∑μ(sˉ)a∑π(a∣sˉ)p(s∣sˉ,a),for all s∈S(7.2)
这个方程组可以求解预期访问量 μ ( s ) \mu(s) μ(s)。那么,策略上的分布就是在每个状态下花费的时间分数,归一化为1,
μ ( s ) = μ ( s ) ∑ s ′ μ ( s ′ ) , for all s ∈ S (7.3) \mu(s) = \frac{\mu(s)}{\sum_{s'}\mu(s')}, \text{for all }s \in \mathcal{S} \tag{7.3} μ(s)=∑s′μ(s′)μ(s),for all s∈S(7.3)
这是没有经过折扣的。如果有折扣率 ( γ < 1 ) (\gamma<1) (γ<1),则应视为一种终止形式,只要在 ( 7.2 ) (7.2) (7.2)的第二项中加入一个关于 γ \gamma γ的系数即可。
继续性和偶发性这两种情况表现相似,但在近似的情况下,它们必须在形式分析中分开处理,我们将在这个部分反复讨论。
但并不完全确信 V E ‾ \overline{VE} VE是强化学习的正确性能目标。我们学习价值函数的最终目的是为了找到一个更好的策略。这个目标的最佳价值函数不一定是最小化 V E ‾ \overline{VE} VE的最佳价值函数。尽管如此,目前还不清楚价值预测的更有用的替代目标可能是什么。所以目前,我们将重点讨论 V E ‾ \overline{VE} VE。
就 V E ‾ \overline{VE} VE而言,一个理想的目标是找到一个全局最优值,即一个权重向量 w ∗ \text{w}^* w∗,对于所有可能的 w \text{w} w来说, V E ‾ ( w ∗ ) ≤ V E ‾ ( w ) \overline{VE}(\text{w}^*) \leq \overline{VE}(\text{w}) VE(w∗)≤VE(w)。对于简单的函数逼近器,如线性函数逼近器,达到这个目标有时是可能的,但对于复杂的函数逼近器,如人工神经网络和决策树,则很少可能。复杂函数逼近器可能会寻求收敛到一个局部最优值,即对于 w ∗ \text{w}^* w∗的某个邻域内的所有 w \text{w} w,其权重向量 w ∗ \text{w}^* w∗的 V E ‾ ( w ∗ ) ≤ V E ‾ ( w \overline{VE}(\text{w}^* )\leq \overline{VE}(\text{w} VE(w∗)≤VE(w) 。虽然这种保证只是稍微让人放心,但对于非线性函数逼近器来说,这通常是最好的保证,而且通常已经足够了。不过,对于强化学习中的许多案例来说,并不能保证收敛到最优值,甚至不能保证收敛到最优值的一定距离内。一些方法事实上可能会出现分歧,其 V E ‾ \overline{VE} VE在极限中接近于无穷大。
之前我们概述了一个框架,用于价值预测的各种强化学习方法与各种函数逼近方法相结合,利用前者的更新为后者生成训练实例。我们还描述了这些方法可能渴望最小化的 V E ‾ \overline{VE} VE性能测量。可能的函数逼近方法的范围太大了,无法涵盖所有的方法,而且无论如何,我们对大多数方法的了解太少,无法做出可靠的评估或推荐。必要时,我们只考虑几种可能性。所以,我们重点讨论基于梯度原理的函数逼近方法,特别是线性梯度下降法。我们之所以关注这些方法,部分原因是我们认为它们特别有前途,而且它们揭示了关键的理论问题。
7.2 随机梯度下降和半梯度下降
我们现在详细地探讨一类用于价值预测中的函数逼近的学习方法,即随机梯度下降(SGD) 方法。SGD方法是所有函数逼近方法中应用最广泛的方法之一,特别适合在线强化学习。
在梯度下降方法中,权重向量是一个具有固定数量实值分量的列向量, w ≐ ( w 1 , w 2 , . . , w d ) T \text{w} \doteq (w_1, w_2, . . ,w_d)^T w≐(w1,w2,..,wd)T,近似价值函数 v ^ ( s , w ) \hat{v}(s,w) v^(s,w)是所有 s ∈ S s \in \mathcal{S} s∈S的 w \text{w} w的一个可微函数,我们将在一系列离散时间步长的每一个步长更新 w \text{w} w, t = 0 , 1 , 2 , 3 , . . . . . . t = 0, 1, 2, 3, ...... t=0,1,2,3,......,因此我们需要一个记号 w t \text{w}_t wt来表示每一步的权重向量。现在,让我们假设,在每一步,我们观察到一个新的例子 S t → v π ( S t ) S_t \to v_\pi(S_t) St→vπ(St),包括一个(可能是随机选择的)状态 S t S_t St及其在策略下的真实值。这些状态可能是来自与环境交互的连续状态,但现在我们不做这样的假设。即使我们得到了每个 S t S_t St的精确的、正确的值 v π ( S t ) v_\pi(S_t) vπ(St),但仍然存在一个困难的问题,因为我们的函数逼近器的资源有限,因此解决的方法也有限。特别是,一般来说,没有一个 w \text{w} w可以完全正确地得到所有的状态,甚至所有的例子。此外,我们必须泛化到所有其他没有出现在例子中的状态。
我们假设状态出现在具有相同分布的例子中,如(7.1)所示,我们试图使 V E ‾ \overline{VE} VE最小化。在这种情况下,一个好的策略是尽量减少观察到的示例的错误。随机梯度下降(SGD)方法通过在每个例子后向最能减少该例子误差的方向调整少量的权值向量来做到这一点
w t + 1 ≐ w t − 1 2 α ∇ [ v π ( S t ) − v ^ ( S t , w t ) ] 2 = w t + α [ v π ( S t ) − v ^ ( S t , w t ) ] ∇ v ^ ( S t , w t ) (7.4, 7.5) \begin{aligned}\text{w}_{t+1}& \doteq \text{w}_{t}-\frac{1}{2}\alpha \nabla[v_{\pi}(S_t)-\hat{v}(S_t, \text{w}_t)]^2\\ & =\text{w}_{t} + \alpha[v_\pi(S_t)-\hat{v}(S_t, \text{w}_{t})]\nabla\hat{v}(S_t, \text{w}_{t})\end{aligned} \tag{7.4, 7.5} wt+1≐wt−21α∇[vπ(St)−v^(St,wt)]2=wt+α[vπ(St)−v^(St,wt)]∇v^(St,wt)(7.4, 7.5)
其中 α \alpha α是一个正的步长参数,对于任何标量表达式 f ( w ) f(\text{w}) f(w)是一个向量的函数(这里是 w t \text{w}_{t} wt), ∇ f ( w ) \nabla f(\text{w}) ∇f(w)表示该表达式对该向量分量的偏导数的列向量,
∇ f ( w ) ≐ ( ∂ f ( w ) ∂ w 1 , ∂ f ( w ) ∂ w 2 , . . . , ∂ f ( w ) ∂ w d ) T (7.6) \nabla f(\text{w}) \doteq (\frac{\partial f(\text{w})}{\partial w_1},\frac{\partial f(\text{w})}{\partial w_2}, ..., \frac{\partial f(\text{w})}{\partial w_d})^T \tag{7.6} ∇f(w)≐(∂w1∂f(w),∂w2∂f(w),...,∂wd∂f(w))T(7.6)
这个导数向量是 f f f相对于 w \text{w} w的梯度,SGD方法是“梯度下降”方法,因为 w t \text{w}_t wt的总体步长与实例平方误差的负梯度成正比(7.4)。这是误差下降最快的方向。梯度下降法在更新时被称为"随机方法",就像这里一样,只对一个例子进行更新,而这个例子可能是随机选择的。在许多例子中,总体效果是使平均性能衡量标准(如 V E ‾ \overline{VE} VE)最小化。
可能不会立即明白为什么SGD只在梯度方向上进行一点移动。我们是否可以不向这个方向全部移动,完全消除例子上的误差?在许多情况下,可以这样做,但通常这是不可取的。我们并不寻求或期望找到一个对所有状态都有零误差的价值函数,而只是一个能平衡不同状态下误差的近似值。如果我们完全修正每个例子,那么就找不到一个平衡。事实上,SGD方法的收敛结果是假设随着时间的推移而减小的。如果它以满足标准随机近似条件的方式减小,那么SGD方法(7.5)保证收敛到局部最优。
现在我们来看看第 t t t个训练例子的目标输出(这里表示为 U t ∈ R U_t \in \mathbb{R} Ut∈R) S t → U t S_t \to U_t St→Ut,不是真实值 v π ( S t ) v_\pi (S_t) vπ(St),而是一些可能是随机的近似值。例如, U t U_t Ut可能是 v π ( S t ) v_\pi(S_t) vπ(St)的噪声破坏版本,也可能是之前提到的使用 v ^ \hat{v} v^的引导目标之一。在这些情况下,我们不能执行精确的更新(7.5),因为 v π ( S t ) v_\pi(S_t) vπ(St)是未知的,但我们可以通过用 U t U_t Ut代替 v ( S t ) v(S_t) v(St)来近似它。这就得到了下面的状态值预测的一般SGD方法。
w t + 1 ≐ w t + α [ U t − v ^ ( S t , w t ) ] ∇ v ^ ( S t , w t ) (7.7) \text{w}_{t+1} \doteq \text{w}_{t} + \alpha[U_t-\hat{v}(S_t, \text{w}_{t})]\nabla\hat{v}(S_t, \text{w}_{t}) \tag{7.7} wt+1≐wt+α[Ut−v^(St,wt)]∇v^(St,wt)(7.7)
如果 U t U_t Ut是一个无偏估计,也就是说,如果 E [ U t ∣ S t = s ] = v π ( S t ) \mathbb{E}[U_t|S_t=s] = v_\pi(S_t) E[Ut∣St=s]=vπ(St),对于每一个 t t t,那么在通常的随机逼近条件下,保证 w t \text{w}_t wt收敛到一个局部最优的递减 。
例如,假设例子中的状态是使用策略与环境交互(或模拟交互)产生的状态 。因为一个状态的真实值是它之后收益的预期值,所以蒙特卡洛目标 U t ≐ G t U_t \doteq G_t Ut≐Gt根据定义是 v π ( S t ) v_\pi(S_t) vπ(St)的无偏估计。在这种选择下,一般SGD方法(7.7)收敛到 v π ( S t ) v_\pi(S_t) vπ(St)的局部最优近似。因此,蒙特卡洛状态值预测的梯度下降版本可以保证找到一个局部最优解。完整算法的伪代码如下所示。
关于 v ^ ≈ v π \hat{v} \approx v_\pi v^≈vπ的梯度蒙特卡罗算法

如果用 v π ( S t ) v_\pi(S_t) vπ(St)的引导估计作为(7.7)中的目标 U t U_t Ut,则不能得到同样的保证。引导目标如n步返回 G t : t + n G_{t:t+n} Gt:t+n或DP目标 ∑ a , s ′ , r ( a ∣ S t ) p ( s ′ , r ∣ S t , a ) [ r + γ v ^ ( s ′ , w t ) ] \sum_{a,s',r}(a|S_t)p(s',r|S_t,a)[r+\gamma \hat{v}(s',\text{w}_t)] ∑a,s′,r(a∣St)p(s′,r∣St,a)[r+γv^(s′,wt)]都取决于权重向量 w t \text{w}_t wt的当前值,这意味着它们会有偏差,它们不会产生真正的梯度下降法。从(7.4)到(7.5)的关键步骤是依赖于目标与 w t \text{w}_t wt无关。引导法实际上并不是真正的梯度下降法(Barnard, 1993)。它们考虑了改变权重向量 w t \text{w}_t wt对估计的影响,但忽略了它对目标的影响。它们只包括梯度的一部分,因此,我们称它们为半梯度方法(semi-gradient methods)。
虽然半梯度(bootstrapping)方法不像梯度方法那样稳健地收敛,但在重要的情况下,如之后讨论的线性情况下,它们确实可靠地收敛。此外,它们还具有一些重要的优势,使它们经常受到人们的青睐。其中一个原因是,它们通常能够显著加快学习速度。另一个原因是,它们使学习能够持续进行,并且是在线学习,而不需要等待一个事件的结束。这使得它们能够用于持续的问题,并提供计算上的优势。一个典型的半梯度方法是半梯度TD(0),它使用 U t ≐ R t + 1 + γ v ^ ( S t + 1 , w ) U_t \doteq R_{t+1} + \gamma \hat{v}(S_{t+1},\text{w}) Ut≐Rt+1+γv^(St+1,w)作为目标。这个方法的完整伪代码在下面给出。
关于TD(0)见强化学习(五) - 时序差分学习
关于 v ^ ≈ v π \hat{v} \approx v_\pi v^≈vπ的半梯度TD(0)算法

状态收敛(State aggregation) 是一种简单的泛函逼近形式,将状态进行分组,每组有一个估计值(权重向量 w \text{w} w的一个分量)。一个状态的值估计为它的组s分量,当状态更新时,只更新该分量。状态收敛是SGD(7.7)的一种特殊情况,其中梯度 ∇ v ^ ( S t , w t ) \nabla \hat{v}(S_t,\text{w}_t) ∇v^(St,wt),对于 S t S_t St组s分量为1,其他分量为0。
例7.1: 1000态随机行走的状态收敛
考虑随机行走任务的1000态版本。状态的编号从1到1000,从左到右,所有的事件都从中心附近的状态500开始。状态转换是从当前状态到它左边的100个邻近状态之一,或者到它右边的100个邻近状态之一,所有的概率都是相等的。当然,如果当前状态靠近一个边缘,那么它那一边的邻居可能少于100个。在这种情况下,所有进入这些缺失的邻域的概率都会进入终止在那一边的概率中(因此,状态1有0.5的机会终止在左边,状态950有0.25的机会终止在右边)。在左边终止会产生1的奖励,在右边终止会产生+1的奖励。所有其他转折的奖励为零。在本节中,我们将这个任务作为一个运行的例子。
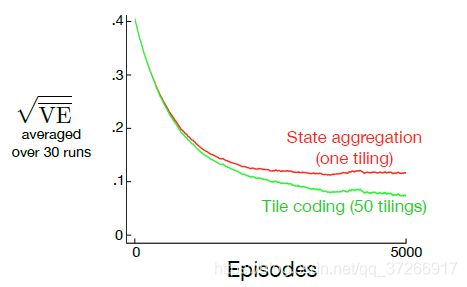
图7.3显示了这个任务的价值函数 v π v_\pi vπ。它几乎是一条直线,但在最后100个状态的每一端都略微向水平方向弯曲。同时显示的是由梯度蒙特卡洛算法学习到的最终近似值函数,并在100000次发作后进行状态收敛,步长大小为 α = 2 × 1 0 − 5 \alpha =2 \times10^{-5} α=2×10−5.对于状态收敛,1000个状态被分成10组,每组100个状态(即状态1-100为一组,状态101-200为另一组,以此类推)。图中所示的阶梯效应是典型的状态聚集,在每组内,近似值是恒定的,从一组到下一组,它的变化很突然。这些近似值接近 V E ‾ \overline{VE} VE的全局最小值(7.1)。
近似值的一些细节最好通过参考本任务的状态分布 μ μ μ来理解,图中下部以右侧刻度显示。状态500,在中心,是每个事件的第一个状态,但很少再次访问。平均来说,大约有1.37%的时间步数花在起始状态。从起始状态一步就能到达的状态是第二多的访问状态,大约0.17%的时间步数都花在其中的每一个状态上。从那里μ几乎线性下降o,在极端状态1和1000时达到约0.0147%。分布最明显的影响是在最左边的组上,其值明显比组内状态的真实值的未加权平均值偏高,而在最右边的组上,其值明显偏低。这是由于这些区域内的状态被μ加权的不对称性最大。例如,在最左边的组中,状态100的权重是状态1的3倍以上。因此,该组的估计值偏向于状态100的真实值,它比状态1的真实值高。
7.3 线性近似
函数逼近的一个最重要的特殊情况是,逼近函数 v ^ ( ⋅ , w ) \hat{v}(\cdot ,\text{w}) v^(⋅,w)是权重向量w的线性函数。对应于每个状态s,有一个实值向量 x ( s ) ≐ ( x 1 ( s ) , x 2 ( s ) , . . . , x d ( s ) ) T \text{x}(s) \doteq (x_1(s), x_2(s), ... ,x_d(s))^T x(s)≐(x1(s),x2(s),...,xd(s))T,分量与w相同。线性方法通过w和x(s)之间的内积来逼近状态价值函数。
v ^ ( s , w ) ≐ w T x ( s ) ≐ ∑ i = 1 d w i x i ( s ) (7.8) \hat{v}(s, \text{w})\doteq \text{w}^T\text{x}(s)\doteq\sum_{i=1}^{d}w_ix_i(s)\tag{7.8} v^(s,w)≐wTx(s)≐i=1∑dwixi(s)(7.8)
在这种情况下,近似价值函数被称为线性权重(linear in the weights),或者简称为线性。
向量 x ( s ) \text{x}(s) x(s)被称为代表了状态 s s s的 特征向量(feature vector)。 x ( s ) \text{x}(s) x(s)的每个分量 x i ( s ) \text{x}_i(s) xi(s)都是函数 x i : S → R \text{x}_i:\mathcal{S}\to\mathbb{R} xi:S→R的值。我们把一个特征 看作是这些函数中的一个函数的全部,我们把它对一个状态s的值称为s的特征。对于线性方法,特征是基本函数,因为它们构成了近似函数集的线性基础。构建d维特征向量来表示状态,就等于选择了一组d个基函数。特征可以用许多不同的方式来定义,我们在接下来介绍几种可能性。
用线性函数逼近的SGD更新是很自然的。在这种情况下,近似值函数关于w的梯度为
∇ v ^ ( s , w ) = x ( s ) \nabla \hat{v}(s,\text{w}) = \text{x}(s) ∇v^(s,w)=x(s)
因此,在线性情况下,一般的SGD更新(7.7)简化为一种特别简单的形式:
w t + 1 ≐ w t + α [ U t − v ^ ( S t , w t ) ] x ( S t ) . \text{w}_{t+1} \doteq \text{w}_{t} + \alpha[U_t-\hat{v}(S_t, \text{w}_{t})]\text{x}(S_t). wt+1≐wt+α[Ut−v^(St,wt)]x(St).
由于它比较简单,线性SGD情况是最有利的数学分析。对于各种学习系统,几乎所有有用的收敛结果都适用于线性(或更简单的)函数逼近方法。
特别是,在线性情况下,只有一个最优值(或者,在退化情况下,有一组同样好的最优值),因此,任何保证收敛到局部最优值或接近局部最优值的方法都会自动保证收敛到全局最优值或接近全局最优值。例如,上一节介绍的梯度蒙特卡罗算法在线性函数逼近下收敛到 V E ‾ \overline{VE} VE的全局最优,如如果按照通常的条件, α \alpha α随时间减少。
上一节提出的半梯度TD(0)算法在线性函数逼近下也是收敛的,但这与一般的结果并不一致
SGD;所以一个单独的定理是必要的。收敛到的权值向量也不是全局最优,而是接近局部最优的一点。更详细地考虑这个重要的情况是有用的,特别是对于继续的情况。 t t t时刻的更新为
w t + 1 ≐ w t + α ( R t + 1 + γ w t T x t + 1 − w t T x t ) x t = w t + α ( R t + 1 x t − x t ( x t − γ x t + 1 ) T w t ) (7.9) \begin{aligned}\text{w}_{t+1} & \doteq \text{w}_t + \alpha(R_{t+1} + \gamma \text{w}_{t}^T\text{x}_{t+1}-\text{w}_{t}^T\text{x}_t)\text{x}_t\\&=\text{w}_t +\alpha (R_{t+1}\text{x}_t- \text{x}_t(\text{x}_t-\gamma\text{x}_{t+1})^T\text{w}_t)\end{aligned} \tag{7.9} wt+1≐wt+α(Rt+1+γwtTxt+1−wtTxt)xt=wt+α(Rt+1xt−xt(xt−γxt+1)Twt)(7.9)
这里我们用了符号简写 x t = x ( S t ) \text{x}_t = \text{x}(S_t) xt=x(St)。一旦系统达到稳定状态,对于任何给定的 w t \text{w}_t wt,预期的下一个权重向量可以写成
E [ w t + 1 ∣ w t ] = w t + α ( b − A w t ) (7.10) \mathbb{E}[\text{w}_{t+1}|\text{w}_t] = \text{w}_t + \alpha(b-A\text{w}_t) \tag{7.10} E[wt+1∣wt]=wt+α(b−Awt)(7.10)
其中
b ≐ E [ R t + 1 x t ] ∈ R d and A ≐ E [ x t ( x t − γ x t + 1 ) T ] ∈ R d × R d (7.11) b\doteq \mathbb{E}[R_{t+1}\text{x}_t]\in \mathbb{R}^d \ \ \text{ and } \ \ \ A \doteq \mathbb{E}[\text{x}_t(\text{x}_t - \gamma\text{x}_{t+1})^T] \in \mathbb{R}^d \times \mathbb{R}^d \tag{7.11} b≐E[Rt+1xt]∈Rd and A≐E[xt(xt−γxt+1)T]∈Rd×Rd(7.11)
由式(7.10)可知,如果系统收敛,则必然收敛到权向量 w T D \text{w}_{TD} wTD处
b − A w T D = 0 ⇒ b = A w T D ⇒ w T D = A − 1 b . (7.12) \begin{aligned} b - A \text{w}_{TD} & = 0\\ \Rightarrow \qquad \qquad \qquad b &= A \text{w}_{TD} \\ \Rightarrow \qquad \qquad \ \ \text{w}_{TD} & =A^{-1}b. \end{aligned} \tag{7.12} b−AwTD⇒b⇒ wTD=0=AwTD=A−1b.(7.12)
这个量叫做TD定点(TD fixed point)。事实上,线性半梯度TD(0)收敛于此点。框中给出了一些证明其收敛性的理论,以及上述逆的存在。
线性TD(0)收敛性的证明
什么性质保证线性TD(0)算法(7.9)的收敛?可以通过将(7.10)重写为
E [ w t + 1 ∣ w t ] = ( I − α A ) w t + α b . (7.13) \mathbb{E}[\text{w}_{t+1}|\text{w}_t] = (I - \alpha A)\text{w}_t+ \alpha b. \tag{7.13} E[wt+1∣wt]=(I−αA)wt+αb.(7.13)
注意,矩阵A乘以权重向量wt而不是b;只有A对收敛很重要。为了发展直观性,考虑 A A A是一个对角矩阵的特殊情况。如果任何一个对角线元素是负的,那么相应对角线元素将大于1, w t \text{w}_t wt的相应分量将被放大,如果继续下去将导致不收敛。另一方面,如果 A A A的对角线元素都是正数,那么 α α α可以选择比其中最大的元素小一的元素,这样对角线上的元素 I − α A I- \alpha A I−αA都在0和1之间,在这种情况下,更新的第一项趋向于缩小 w t \text{w}_t wt,稳定性得到保证。一般来说,只要 A A A是正定的,即 y T A y > 0 y^TAy>0 yTAy>0,对于任何 y ≠ 0 y \not = 0 y=0的实向量, w t \text{w}_t wt就会向零趋近,正定性也保证了逆 A − 1 A^{-1} A−1的存在。
对于线性TD(0),在连续的情况下, γ < 1 \gamma<1 γ<1,A矩阵(7.11)可以写成
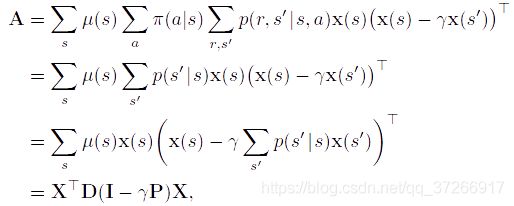
其中 μ ( s ) μ(s) μ(s)是策略 π \pi π下的稳态分布, p ( s ′ ∣ s ) p(s' |s) p(s′∣s)是策略 π \pi π下从 s s s过渡到 s ′ s' s′的概率, P P P是这些概率的 ∣ S ∣ × ∣ S ∣ |\mathcal{S}|\times|\mathcal{S}| ∣S∣×∣S∣矩阵, D D D是 μ ( s ) μ(s) μ(s)在对角线上的| ∣ S ∣ × ∣ S ∣ |\mathcal{S}|\times|\mathcal{S}| ∣S∣×∣S∣对角线矩阵, X X X是以 x ( s ) \text{x}(s) x(s)为行的 ∣ S ∣ × d |\mathcal{S}|\times d ∣S∣×d矩阵。从这里可以看出,内矩阵 D ( I − γ P ) D(I -\gamma P) D(I−γP)是决定A的正定性的关键。
对于这种形式的关键矩阵,如果它的所有列的总和都是非负数,那么正定性就得到了保证。这是由Sutton(1988年,第27页)根据以前建立的两个定理证明的。其中一个定理说,如果且仅当对称矩阵 S = M + M T S=M+M^T S=M+MT是正定的时候,任何矩阵M都是正定的(Sutton 1988,附录)。第二个定理说,任何对称实型矩阵S,如果它的所有对角线项都是正数,并且大于相应的离角线项的绝对值之和,那么它就是正定的(Varga 1962,第23页)。对于我们的关键矩阵, D ( I − γ P ) D(I -\gamma P) D(I−γP),对角线项是正的,非对角线项是负的,所以我们要证明的是每个行和加上相应的列和是正的。由于 P P P是一个随机矩阵,且 γ < 1 \gamma<1 γ<1,所以行和都是正数。因此只需证明列和为非负值即可。请注意,任何矩阵M的列和的行向量可以写成 1 T M 1^TM 1TM,其中1是所有分量都等于1的列向量。让 μ μ μ表示 μ ( s ) μ(s) μ(s)的 ∣ S ∣ |\mathcal{S}| ∣S∣-向量,其中 μ = P T μ μ=P^Tμ μ=PTμ,凭借 μ μ μ是稳态分布。那么,我们的关键矩阵的列和为
其所有分量均为正值。因此,关键矩阵及其 A A A矩阵是正定的,策略上TD(0)是稳定的。(要证明收敛的概率为1,还需要附加条件和随时间减少的时间表)。
在TD定点,(在连续情况下)也证明了 V E ‾ \overline{VE} VE在最小可能误差的有界扩展范围内:
V E ‾ ( w T D ) ≤ 1 1 − γ min w V E ‾ ( w ) (7.14) \overline{VE}(\text{w}_{TD})\leq\frac{1}{1-\gamma}\min_{\text{w}}\overline{VE}(\text{w}) \tag{7.14} VE(wTD)≤1−γ1wminVE(w)(7.14)
也就是说,TD方法的渐近误差不超过蒙特卡洛方法在极限情况下达到的最小可能误差的 1 1 − γ \frac{1}{1-\gamma} 1−γ1倍。由于 γ \gamma γ经常接近1,这个扩展因子可能相当大,所以TD方法的渐近性能有很大的潜在损失。另一方面,回顾一下,与蒙特卡罗方法相比,TD方法的方差通常大大降低,因此速度更快。哪种方法最好,取决于近似和问题的性质,以及学习持续的时间。
类似于(7.14)的约束也适用于其他on-policy的引导方法。例如,线性半梯度DP(式7.7,有 U t ≐ ∑ a π ( a ∣ S t ) ∑ s ′ , r p ( s ′ , r ∣ S t , a ) [ r + γ v ^ ( s ′ , w t ) ] U_t \doteq \sum_{a} \pi (a|S_t) \sum_{s',r} p(s', r|S_t, a)[r+ \gamma \hat{v}(s',\text{w}_t)] Ut≐∑aπ(a∣St)∑s′,rp(s′,r∣St,a)[r+γv^(s′,wt)])根据on-policy分布进行更新,也将收敛到TD定点。一步半梯度动作值方法,如之后所涉及的半梯度Sarsa(0),会收敛到一个类似的定点和一个类似的边界。对于事件性任务,有一个稍微不同但相关的边界(见Bertsekas和Tsitsiklis,1996)。还有一些关于奖励、特征和步长参数减少的技术条件,我们在这里省略了。
这些收敛结果的关键在于状态是根据on-policy的分布进行更新的。对于其他的更新分布,使用函数近似的引导方法实际上可能会偏离到无穷大。
7.4 线性方法的特征构造
线性方法之所以有趣,是因为它们的收敛性保证,但也因为在实践中它们在数据和计算方面都可以非常高效。是否如此,关键取决于如何用特征来表示状态,我们在这一大节中研究了这个问题。选择适合于任务的特征是为强化学习系统添加先验领域知识的重要方式。直观地说,特征应该对应于状态空间的各个方面,沿着这些方面进行泛化可能是合适的。例如,如果我们对几何物体进行估值,我们可能希望对每一种可能的形状、颜色、大小或功能都有特征。如果我们对一个移动机器人的状态进行估值,那么我们可能希望有位置、剩余电池电量、最近声纳读数等特征。
线性形式的一个局限性是,它不能考虑到任何特征之间的相互作用,例如特征 i i i的存在只有在没有特征 j j j的情况下才是好的。例如,在极点平衡任务中,高的角速度的好坏不是确定的,这取决于角度。如果角度很高,那么高角速度就意味着即将有坠落的危险,是一种坏的状态,而如果角度很低,那么高角速度就意味着极点正在自正,是一种好的状态。但线性价值函数就无法分别单独对角度和角速度进行特征的编码。相反,它需要或者另外需要这两个基本状态维度组合的特征。在下面的小节中,我们考虑了各种一般的方法来实现这一点。
7.4.1 Coarse Coding(粗编码)
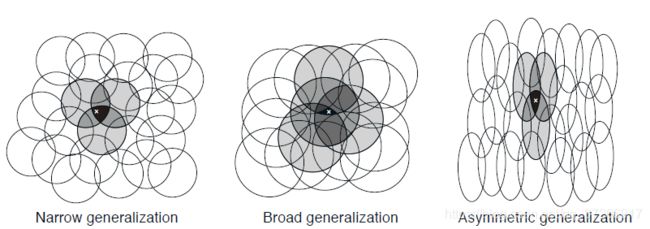
考虑一个任务,其中状态集的自然表示是一个连续的二维空间。这种情况下的一种表示方法是由状态空间中的圆圈对应的特征组成,如图(7.2)所示。如果状态在圆圈内,则对应的特征值为1,称其存在;否则特征值为0,称其不存在。这种1 0值的特征称为二进制特征。给定一个状态,哪种二元特征存在,就表示该状态在哪个圈内,从而粗略地对其位置进行编码。用这样重叠的特征来表示一个状态(尽管它们不一定是圆圈或二进制),称为粗编码(coarse coding)。
假设线性梯度递减函数近似,考虑圆圈的大小和密度的影响。与每个圆对应的是受学习影响的单个权值(w的一个分量)。如果我们在一个状态下进行训练,即空间中的一个点,那么所有与该状态相交的圆的权重都会受到影响。因此,通过(7.8),近似价值函数会影响到圆并集内的所有状态,一个点与该状态的共有的圆越多,其影响越大,如图7.2所示。如果圆圈较小,则泛化的距离较短,如图7.3(左),而如果圆圈较大,则泛化的距离较大,如图7.3(中)。此外,特征的形状将决定泛化的性质。例如,如果它们不是严格意义上的圆形,而是在一个方向上被拉长,那么泛化将同样受到影响,如图7.3(右)。
接受野较大的特征可以得到广泛的泛化,但似乎也会将学习函数限制在一个粗糙的近似值上,无法做出比接受野的宽度更细的分辨。较好的一点是,事实并非如此。从一个点到另一个点的初始泛化确实受到接受野的大小和形状的控制,但敏锐度,即最终可能的最精细的辨别,则更多地受到特征总数的控制。
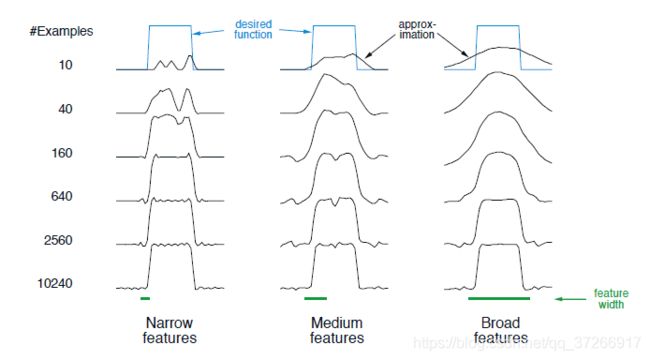
例7.2:粗编码的粗度
本例说明了粗编码中感受场的大小对学习的影响。基于粗编码和(7.7)的线性函数近似被用来学习一维方波函数(如图7.4顶部所示)。该函数的值被用作目标, U t U_t Ut。只有一个维度,接受野是间隔而不是圆。如图底部所示,用三种不同大小的区间重复学习:窄、中、宽,。所有这三种情况下,特征的密度相同,约有50在被学习的函数范围内。训练实例在这个范围内统一随机生成。步长大小参数为 α = 0.2 n \alpha=\frac{0.2}{n} α=n0.2 ,其中 n n n为一次出现的特征数。图7.4显示了所有三种情况下学习的函数在学习过程中的情况。请注意,特征的宽度在学习早期有很大的影响。在特征宽的情况下,泛化趋于宽泛;在特征窄的情况下,只改变了每个训练点的近邻,导致学习到的函数更加凹凸不平。然而,最终学习到的函数只受到特征宽度的轻微影响。接受野形状往往对泛化有很大的影响,但对渐近解质量影响不大。
7.4.2 Tile Coding(瓦片编码)
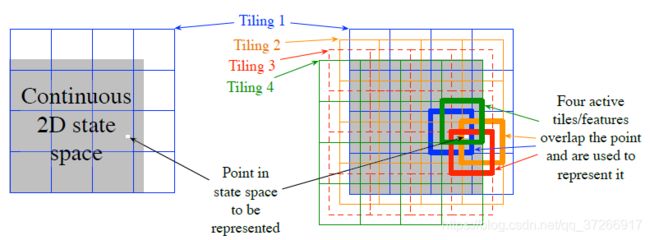
瓦片编码(Tile Coding) 是多维连续空间的一种粗编码形式,它具有灵活性和计算效率。它可能是现代顺序数字计算机最实用的特征表示方法。在瓦片编码中,特征的接受野被分组为状态空间的分区。每一个这样的分区称为瓦片,分区的每个元素称为瓦片。例如,二维状态空间最简单的瓦片是一个均匀的网格,如图7.5左侧所示。这里的瓦片或接受野是正方形而不是图7.2中的圆形。如果只用这一个瓦片,那么白点所表示的状态将由它所在瓦片的单一特征来表示;泛化将完成到同一瓦片内的所有状态,而对瓦片外的状态则不存在。如果只用一个瓦片,我们就不会有粗编码,而只是一个状态集合的情况。
为了获得粗编码的优势,需要重叠的接受野,并且通过定义,分区的瓦片不重叠。 为了通过瓦片编码获得真正的粗编码,使用了多个瓦片,每个瓦片都偏移了一小部分。 图7.5的右侧显示了一个带有四个拼贴的简单案例。 每个状态(例如,由白点指示的状态)都恰好落在四个瓦片中的每个瓦片中。 这四个瓦片对应于在状态发生时变为活动的四个功能。 具体来说,特征向量 x ( s ) \text{x}(s ) x(s)在每个切片中的每个切片具有一个分量。 在此示例中,有 4 × 4 × 4 = 64 4×4×4 = 64 4×4×4=64个分量,除了与 s s s所属于的瓦片相对应的四个分量外,其余全部为0。 图7.6显示了在1000状态随机游动示例中,多个偏移瓦片(粗编码)比单个瓦片的优势。
瓦片编码的直接实际优势是,因为它可与分区一起使用,所以一次激活的功能总数对于任何状态都是相同的。每瓦片中仅存在一个特征,因此存在的特征总数始终与瓦片数相同。这允许以简单,直观的方式设置步长参数α。例如,选择 α = 1 n α=\frac{1}{n} α=n1,其中 n n n是瓦片的数量。如果对示例 s → v s→v s→v进行训练,则无论先前的估计 v ^ ( s , w t ) \hat{v}(s,\text{w}_t) v^(s,wt),新的估计都将为 v ^ ( s , w t + 1 ) = v \hat{v}(s,\text{w}_{t+1}) = v v^(s,wt+1)=v。通常,人们希望改变得更慢,从而允许目标输出泛化和随机变化。例如,假设可能选择 α = 1 10 n α=\frac{1}{10n} α=10n1,在这种情况下,对训练状态的估计将在一次更新中移动到目标的十分之一,而相邻状态的移动将减少,与它们共同拥有的瓦片数量成比例。
瓦片编码还通过使用二进制特征向量而获得了计算优势。由于每个分量为0或1,因此构成近似价值函数(7.8)的加权和几乎是可以忽略的。与其执行 d d d个乘法和加法,不如简单地计算 n < < d n << d n<<d个活动特征的索引,然后将权重向量的 n n n个对应分量相加。
如果这些状态属于任何一个相同的瓦片内,则会发生泛化,泛化程度与共同的瓦片数量成正比,而不是训练的状态。即使选择如何彼此瓦片也会影响泛化。如果它们在各个维度上的偏移量相同,如图7.5所示,则不同的状态可以以定性的不同方式泛化,如图7.7的上半部分所示。八个子图中的每个子图都显示了从受训状态到附近点的概括模式。在此示例中,有八个切片,因此,一个切片中的64个子区域具有明显的概括性,但所有子区域均根据这八个模式中的一种。请注意,均匀的偏移会在许多样式中导致沿对角线产生强烈的影响。如图下半部分所示,如果瓦片瓦片不对称,可以避免这些伪影。下面的泛化模式更好,因为它们都很好地集中在受训练的状态上,没有明显的不对称性。

在所有情况下,瓦片在每个维度上的偏移量都是瓦片宽度的一小部分。如果 w w w表示瓦片宽度, n n n表示瓦片数,则 w n \frac{w}{n} nw是基本单位。在一侧的小方块 w n \frac{w}{n} nw中,所有状态均激活相同的瓦片,具有相同的特征表示和相同的近似值。如果状态由 w n \frac{w}{n} nw沿任意笛卡尔方向移动,则特征表示将按一个组件/瓦片块变化。均匀偏置的瓦片彼此之间的偏移正是这个单位距离。对于二维空间,我们说每个瓦片都由位移矢量(1, 1)进行偏移,这意味着它是与前一个瓦片相比较的,其位移是该向量的 w n \frac{w}{n} nw倍。用这些术语,图7.7下部所示的非对称瓦片瓦片的位移矢量为(1, 3)。
在选择拼贴策略时,必须选择拼贴的数量和瓦片的形状。瓦片的数量以及瓦片的大小决定了渐近逼近的分辨率或精细度,如一般的粗编码所示,如图7.8所示。瓦片的形状将决定泛化的性质。如图7.7(下图)所示,正方形瓦片在每个尺寸上的推广效果大致相同。沿着一个维度拉长的瓦片,例如图7.8中的条纹瓦片(中间),将促进沿着该维度的泛化。图7.8中的瓦片(中间)在左侧也更密集和更细,从而在沿水平方向的尺寸较低的位置上促进了水平方向的辨别。图7.8(右)中的对角条纹拼贴将促进沿一个对角线的泛化。在更高的尺寸中,与轴对齐的条纹对应于忽略某些瓦片中的某些尺寸,即对应于超平面切片。如图7.8(左)所示的不规则瓦片也是可行的,尽管在实践中很少见并且超出了一般标准软件的应用。
在实践中,通常需要在不同的瓦片中使用不同形状的瓦片。例如,可能使用一些垂直条纹拼贴和一些水平条纹拼贴。这将鼓励沿任一维度进行概括。但是,仅凭条形瓦片就不可能得知水平坐标和垂直坐标的特定结合具有独特的值(无论学到什么,它都会渗入具有相同水平坐标和垂直坐标的状态)。为此,需要诸如图7.5所示的矩形矩形块。有了多个瓦片(一些水平,一些垂直和一些合取),智能体就可以得到所有东西:可以沿每个维度进行泛化的偏好,但也可以学习用于连接的特定值。切片的选择决定了概括性,并且在此选择可以有效实现自动化之前,重要的是,切片编码可以使选择变得灵活且对人们有意义。
减少内存需求的另一个有用技巧是散列-将大瓦片一致地伪随机散列为小得多的瓦片。散列产生的瓦片由在一个瓦片空间的一个状态随机分布在整个状态中的连续的,不相交的区域组成,但仍然形成了详尽的分区。例如,一个瓦片可能包含下图所示的四个子瓦片。
通过散列,通常会在不损失性能的情况下,通过大量因素降低内存需求。这是可能的,因为仅在状态空间的一小部分就需要高分辨率。散列使我们摆脱了维数的限制,因为内存需求不必在维数上成指数关系,而只需要与任务的实际需求相匹配即可。瓦片编码的开源实现通常包括有效的哈希。
7.4.3 实例:Tile Coding实例
本实例采用Acrobot-v1环境,acrobot系统包括两个关节和两个连杆,其中两个连杆之间的连杆是驱动的。最初,连杆是向下悬挂的,目标是将较低的连杆的末端摆动到一个给定的高度。

(1) 环境, 动作和状态空间
首先引入环境库
# Import common libraries
import sys
import gym
import numpy as np
import matplotlib.pyplot as plt
创建主函数mian function,查看环境的相关观测空间, 动作空间, 和状态空间,
if __name__ == "__main__":
# Set plotting options
plt.style.use('ggplot')
np.set_printoptions(precision=3, linewidth=120)
# Create an environment
env = gym.make('Acrobot-v1')
env.seed(505)
# Explore state (observation) space
print("State space:", env.observation_space)
print("- low:", env.observation_space.low)
print("- high:", env.observation_space.high)
# Explore action space
print("Action space:", env.action_space)
其结果输出如下
State space: Box(6,)
- low: [ -1. -1. -1. -1. -12.566 -28.274]
- high: [ 1. 1. 1. 1. 12.566 28.274]
Action space: Discrete(3)
注意,状态空间是多维的,大多数维度从-1到1(两个关节的位置),而最后两个维度的范围更大。
(2) 瓦片化
首先让我们设计一种方法,为给定的状态空间创建一个单一的瓦片。这与上节代码中的均匀网格非常相似。惟一的区别是,应该为分割点的每个维度包含一个偏移量。
举个例子来说,如果low = [-1.0, -5.0], high = [1.0, 5.0], bins = (10, 10)然后有offsets = (-0.1, 0.5),然后返回一个由2个NumPy数组(2维)组成的列表,每个数组包含以下分割点(每个维9个分割点):\
[array([-0.9, -0.7, -0.5, -0.3, -0.1, 0.1, 0.3, 0.5, 0.7]),
array([-3.5, -2.5, -1.5, -0.5, 0.5, 1.5, 2.5, 3.5, 4.5])]
注意第一个维度的分割点是如何偏移-0.1,第二个维度的分割点是如何偏移+0.5。这可能意味着我们的一些瓦片(特别是沿着周边的瓦片)部分位于有效状态空间之外,但这是不可避免的,但是没有什么影响。
# 瓦片化函数
def create_tiling_grid(low, high, bins=(10, 10), offsets=(0.0, 0.0)):
return [np.linspace(low[dim], high[dim], bins[dim] + 1)[1:-1] + offsets[dim] for dim in range(len(bins))]
def create_tilings(low, high, tiling_specs):
return [create_tiling_grid(low, high, bins, offsets) for bins, offsets in tiling_specs]
# 以网格形式可视化每个瓦片
def visualize_tilings(tilings):
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = prop_cycle.by_key()['color']
linestyles = ['-', '--', ':']
legend_lines = []
fig, ax = plt.subplots(figsize=(10, 10))
for i, grid in enumerate(tilings):
for x in grid[0]:
l = ax.axvline(x=x, color=colors[i % len(colors)], linestyle=linestyles[i % len(linestyles)], label=i)
for y in grid[1]:
l = ax.axhline(y=y, color=colors[i % len(colors)], linestyle=linestyles[i % len(linestyles)])
legend_lines.append(l)
ax.grid('off')
ax.legend(legend_lines, ["Tiling #{}".format(t) for t in range(len(legend_lines))], facecolor='white', framealpha=0.9)
ax.set_title("Tilings")
plt.show()
return ax
在主函数中
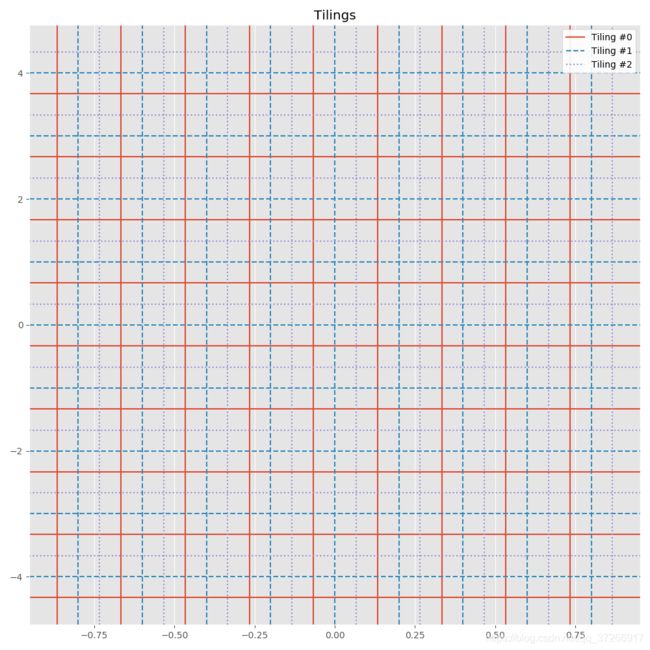
# Tiling specs: [(, ), ...]
tiling_specs = [((10, 10), (-0.066, -0.33)),
((10, 10), (0.0, 0.0)),
((10, 10), (0.066, 0.33))]
tilings = create_tilings(low, high, tiling_specs)
visualize_tilings(tilings)
可视化输出如下,
(3) 瓦片编码
我们需要知道每个样本在不同瓦片上所对应的位置,所以我们就需要获取每个样本在每个瓦片上的索引值.首先我们需要做的是离散化样本,这回方便我们找到每个瓦片上的索引.
'''(3) Tile Encoding'''
# 根据给定的网格离散样本。
def discretize(sample, grid):
return tuple(int(np.digitize(s, g)) for s, g in zip(sample, grid)) # 返回索引值
# 使用瓦片编码对给定的样本进行编码
def tile_encode(sample, tilings, flatten=False):
encoded_sample = [discretize(sample, grid) for grid in tilings]
return np.concatenate(encoded_sample) if flatten else encoded_sample
def visualize_encoded_samples(samples, encoded_samples, tilings, low=None, high=None):
"""Visualize samples by activating the respective tiles."""
samples = np.array(samples) # for ease of indexing
# Show tiling grids
ax = visualize_tilings(tilings)
# If bounds (low, high) are specified, use them to set axis limits
if low is not None and high is not None:
ax.set_xlim(low[0], high[0])
ax.set_ylim(low[1], high[1])
else:
# Pre-render (invisible) samples to automatically set reasonable axis limits, and use them as (low, high)
ax.plot(samples[:, 0], samples[:, 1], 'o', alpha=0.0)
low = [ax.get_xlim()[0], ax.get_ylim()[0]]
high = [ax.get_xlim()[1], ax.get_ylim()[1]]
# Map each encoded sample (which is really a list of indices) to the corresponding tiles it belongs to
tilings_extended = [np.hstack((np.array([low]).T, grid, np.array([high]).T)) for grid in
tilings] # add low and high ends
tile_centers = [(grid_extended[:, 1:] + grid_extended[:, :-1]) / 2 for grid_extended in
tilings_extended] # compute center of each tile
tile_toplefts = [grid_extended[:, :-1] for grid_extended in tilings_extended] # compute topleft of each tile
tile_bottomrights = [grid_extended[:, 1:] for grid_extended in tilings_extended] # compute bottomright of each tile
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = prop_cycle.by_key()['color']
for sample, encoded_sample in zip(samples, encoded_samples):
for i, tile in enumerate(encoded_sample):
# Shade the entire tile with a rectangle
topleft = tile_toplefts[i][0][tile[0]], tile_toplefts[i][1][tile[1]]
bottomright = tile_bottomrights[i][0][tile[0]], tile_bottomrights[i][1][tile[1]]
ax.add_patch(Rectangle(topleft, bottomright[0] - topleft[0], bottomright[1] - topleft[1],
color=colors[i], alpha=0.33))
# In case sample is outside tile bounds, it may not have been highlighted properly
if any(sample < topleft) or any(sample > bottomright):
# So plot a point in the center of the tile and draw a connecting line
cx, cy = tile_centers[i][0][tile[0]], tile_centers[i][1][tile[1]]
ax.add_line(Line2D([sample[0], cx], [sample[1], cy], color=colors[i]))
ax.plot(cx, cy, 's', color=colors[i])
# Finally, plot original samples
ax.plot(samples[:, 0], samples[:, 1], 'o', color='r')
ax.margins(x=0, y=0) # remove unnecessary margins
ax.set_title("Tile-encoded samples")
return ax
使用以下代码来测试
# Test with some sample values
samples = [(-1.2, -5.1),
(-0.75, 3.25),
(-0.5, 0.0),
(0.25, -1.9),
(0.15, -1.75),
(0.75, 2.5),
(0.7, -3.7),
(1.0, 5.0)]
encoded_samples = [tile_encode(sample, tilings) for sample in samples]
print("\nSamples:", repr(samples), sep="\n")
visualize_encoded_samples(samples, encoded_samples, tilings)
其中visualize_encoded_samples为可视化代码,并不需要深究其原理.在完整程序中,我将其放入(1)可视化编码部分,这个部分的作用是方便我们理解代码.
Samples:
[(-1.2, -5.1), (-0.75, 3.25), (-0.5, 0.0), (0.25, -1.9), (0.15, -1.75), (0.75, 2.5), (0.7, -3.7), (1.0, 5.0)]
Encoded samples:
[[(0, 0), (0, 0), (0, 0)], [(1, 8), (1, 8), (0, 7)], [(2, 5), (2, 5), (2, 4)], [(6, 3), (6, 3), (5, 2)], [(6, 3), (5, 3), (5, 2)], [(9, 7), (8, 7), (8, 7)], [(8, 1), (8, 1), (8, 0)], [(9, 9), (9, 9), (9, 9)]]
(4) 使用瓦片编码的Q表
现在需要我们将瓦片编码应用到Q表上,程序如下. 为此我们建立了两个类,QTable类的作用是初始化q表.TiledQTable类的作用是使用瓦片化编码来编辑q表,其中提供了两个操作,分别是,TiledQTable.get()和TiledQTable.update().
TiledQTable.get()的作用是获取在q表上的某个位置的值,类比与上一节离散化中,瓦片化编码的区别是有多个q表,我们需要获得某个状态在各个q表上的值,并取得其均值.TiledQTable.update()的作用是更新瓦片化q表的值,类似于TiledQTable.get(),程序需要同时更新所有瓦片上的q表值.这就是TiledQTable的核心作用.
'''
(4) 使用瓦片编码的Q表
'''
class QTable:
# 初始化Q表
def __init__(self, state_size, action_size):
self.state_size = state_size
self.action_size = action_size
# Create Q-table, initialize all Q-values to zero
self.q_table = np.zeros(shape=(self.state_size + (self.action_size,)))
print("QTable(): size =", self.q_table.shape)
class TiledQTable:
"""组合q表与其内部的瓦片编码"""
# 瓦片化并初始化内部q表。
def __init__(self, low, high, tiling_specs, action_size):
self.tilings = create_tilings(low, high, tiling_specs)
self.state_sizes = [tuple(len(splits)+1 for splits in tiling_grid)
for tiling_grid in self.tilings] # 每片瓦片上的状态数
self.action_size = action_size
self.q_tables = [QTable(state_size, self.action_size)
for state_size in self.state_sizes] # 为每片瓦片建立一个q表
print("TiledQTable(): no. of internal tables = ", len(self.q_tables))
# 得到给定<状态,动作>对的q值。
def get(self, state, action):
# 获取在瓦片上的位置索引
encoded_state = tile_encode(state, self.tilings)
# 检索每片瓦片上的q值,并返回它们的平均值
value = 0.0
for idx, q_table in zip(encoded_state, self.q_tables): # 在每片瓦片上循环
value += q_table.q_table[tuple(idx + (action,))]
value = value / len(self.q_tables) # 计算平均值
return value
# 软更新q值为给定<状态,行动>对的值
def update(self, state, action, value, alpha=0.1):
# 获取在瓦片上的位置索引
encoded_state = tile_encode(state, self.tilings)
# 通过学习率alpha更新每个瓦片上的的q值
for idx, q_table in zip(encoded_state, self.q_tables):
value_ = q_table.q_table[tuple(idx + (action,))] # 获取当前位置q表的值
q_table.q_table[tuple(idx + (action,))] \
+= alpha * value + (1. - alpha) * value_ # 使用学习率更新相关位置的值
使用以下程序测试
# Test with a sample Q-table
tq = TiledQTable(low, high, tiling_specs, 2)
s1 = 3;
s2 = 4;
a = 0;
q = 1.0
print("[GET] Q({}, {}) = {}".format(samples[s1], a,
tq.get(samples[s1], a))) # check value at sample = s1, action = a
print("[UPDATE] Q({}, {}) = {}".format(samples[s2], a, q));
tq.update(samples[s2], a, q) # update value for sample with some common tile(s)
print("[GET] Q({}, {}) = {}".format(samples[s1], a,
tq.get(samples[s1], a))) # check value again, should be slightly updated
输出为
[GET] Q((0.25, -1.9), 0) = 0.0
[UPDATE] Q((0.15, -1.75), 0) = 1.0
[GET] Q((0.25, -1.9), 0) = 0.06666666666666667
(5) Q学习智能体
像上一节一样我们建立Q学习智能体,首先我们要创建QLearningAgent类.要包括如下几个功能,reset_episode,在每个时间开始的时候重置相关变量.reset_exploration重置探索率.act()训练一回合所使用的函数,使用 ε \varepsilon ε贪婪策略选择动作,
'''
(5) Q学习智能体
'''
class QLearningAgent:
def __init__(self, env, tiled_q_table, alpha=0.05, gamma=0.99,
epsilon=1.0, epsilon_decay_rate=0.9995, min_epsilon=.01, seed=505):
"""初始化变量,创建离散化网格。"""
# Environment info
self.env = env
self.state_size = tiled_q_table.state_sizes
self.action_size = self.env.action_space.n # 1-维离散动作空间
self.seed = np.random.seed(seed)
print("--Agent--\nEnvironment:", self.env)
print("State space size:", self.state_size)
print("Action space size:", self.action_size)
# 学习模型参数
self.alpha = alpha # 学习率
self.gamma = gamma # 折扣因子
self.epsilon = self.initial_epsilon = epsilon # 初始探索率
self.epsilon_decay_rate = epsilon_decay_rate # epsilon衰减系数
self.min_epsilon = min_epsilon
# Q表
self.tq = tiled_q_table
def reset_episode(self, state):
"""为新的事件重置变量."""
# 逐步降低探索率
self.epsilon *= self.epsilon_decay_rate
self.epsilon = max(self.epsilon, self.min_epsilon)
# 决定初始行动
self.last_state = state
Q_s = [self.tq.get(state, action) for action in range(self.action_size)]
self.last_action = np.argmax(Q_s)
return self.last_action
def reset_exploration(self, epsilon=None):
"""重置训练时使用的探索率."""
self.epsilon = epsilon if epsilon is not None else self.initial_epsilon
def act(self, state, reward=None, done=None, mode='train'):
"""选择next操作并更新内部Q表 (when mode != 'test')."""
Q_s = [self.tq.get(state, action) for action in range(self.action_size)]
greedy_action = np.argmax(Q_s)
if mode == 'test':
# 测试模式:简单地产生一个动作
action = np.argmax(self.q_table[state])
else:
# 训练模式(默认):更新Q表,选择下一步行动
# Note: 我们用当前状态,回报更新最后的状态动作对的Q表条目
value = reward + self.gamma * max(Q_s)
self.tq.update(self.last_state, self.last_action, value, self.alpha)
# 探索 vs. 利用
do_exploration = np.random.uniform(0, 1) < self.epsilon
if do_exploration:
# 随机选择一个动作
action = np.random.randint(0, self.action_size)
else:
# 从Q表中选择最佳动作
action = greedy_action
# 存储当前状态,下一步操作
self.last_state = state
self.last_action = action
return action
(6)模型训练
最后我们定义模型训练函数
'''
(6) 模型训练
'''
def run(agent, env, num_episodes=10000, mode='train'):
scores = []
max_avg_score = -np.inf
for i_episode in range(1, num_episodes+1):
# 初始化环境
state = env.reset()
action = agent.reset_episode(state)
total_reward = 0
done = False
while not done:
state, reward, done, info = env.step(action)
total_reward += reward
action = agent.act(state, reward, done, mode)
# 保存最终成绩
scores.append(total_reward)
if mode == "train":
if len(scores) > 100:
avg_score = np.mean(scores[-100:])
if avg_score > max_avg_score:
max_avg_score = avg_score
if i_episode % 100 == 0:
print("\rEpisode {}/{} | Max Average Score: {}".format(i_episode, num_episodes, max_avg_score), end="")
sys.stdout.flush()
return scores
(7)完整代码
# Import common libraries
import sys
import gym
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from matplotlib.lines import Line2D
from matplotlib.patches import Rectangle
'''
(1) 可视化函数
'''
# 以网格形式可视化每个瓦片
def visualize_tilings(tilings):
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = prop_cycle.by_key()['color']
linestyles = ['-', '--', ':']
legend_lines = []
fig, ax = plt.subplots(figsize=(10, 10))
for i, grid in enumerate(tilings):
for x in grid[0]:
l = ax.axvline(x=x, color=colors[i % len(colors)], linestyle=linestyles[i % len(linestyles)], label=i)
for y in grid[1]:
l = ax.axhline(y=y, color=colors[i % len(colors)], linestyle=linestyles[i % len(linestyles)])
legend_lines.append(l)
ax.grid('off')
ax.legend(legend_lines, ["Tiling #{}".format(t) for t in range(len(legend_lines))], facecolor='white', framealpha=0.9)
ax.set_title("Tilings")
return ax
def visualize_encoded_samples(samples, encoded_samples, tilings, low=None, high=None):
"""Visualize samples by activating the respective tiles."""
samples = np.array(samples) # for ease of indexing
# Show tiling grids
ax = visualize_tilings(tilings)
# If bounds (low, high) are specified, use them to set axis limits
if low is not None and high is not None:
ax.set_xlim(low[0], high[0])
ax.set_ylim(low[1], high[1])
else:
# Pre-render (invisible) samples to automatically set reasonable axis limits, and use them as (low, high)
ax.plot(samples[:, 0], samples[:, 1], 'o', alpha=0.0)
low = [ax.get_xlim()[0], ax.get_ylim()[0]]
high = [ax.get_xlim()[1], ax.get_ylim()[1]]
# Map each encoded sample (which is really a list of indices) to the corresponding tiles it belongs to
tilings_extended = [np.hstack((np.array([low]).T, grid, np.array([high]).T)) for grid in
tilings] # add low and high ends
tile_centers = [(grid_extended[:, 1:] + grid_extended[:, :-1]) / 2 for grid_extended in
tilings_extended] # compute center of each tile
tile_toplefts = [grid_extended[:, :-1] for grid_extended in tilings_extended] # compute topleft of each tile
tile_bottomrights = [grid_extended[:, 1:] for grid_extended in tilings_extended] # compute bottomright of each tile
prop_cycle = plt.rcParams['axes.prop_cycle']
colors = prop_cycle.by_key()['color']
for sample, encoded_sample in zip(samples, encoded_samples):
for i, tile in enumerate(encoded_sample):
# Shade the entire tile with a rectangle
topleft = tile_toplefts[i][0][tile[0]], tile_toplefts[i][1][tile[1]]
bottomright = tile_bottomrights[i][0][tile[0]], tile_bottomrights[i][1][tile[1]]
ax.add_patch(Rectangle(topleft, bottomright[0] - topleft[0], bottomright[1] - topleft[1],
color=colors[i], alpha=0.33))
# In case sample is outside tile bounds, it may not have been highlighted properly
if any(sample < topleft) or any(sample > bottomright):
# So plot a point in the center of the tile and draw a connecting line
cx, cy = tile_centers[i][0][tile[0]], tile_centers[i][1][tile[1]]
ax.add_line(Line2D([sample[0], cx], [sample[1], cy], color=colors[i]))
ax.plot(cx, cy, 's', color=colors[i])
# Finally, plot original samples
ax.plot(samples[:, 0], samples[:, 1], 'o', color='r')
ax.margins(x=0, y=0) # remove unnecessary margins
ax.set_title("Tile-encoded samples")
return ax
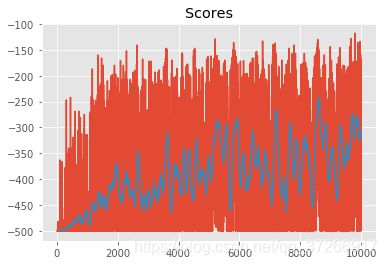
def plot_scores(scores, rolling_window=100):
"""Plot scores and optional rolling mean using specified window."""
plt.plot(scores)
plt.title("Scores")
rolling_mean = pd.Series(scores).rolling(rolling_window).mean()
plt.plot(rolling_mean);
return rolling_mean
'''
(2) Tiling
'''
# 创建瓦片化网格
def create_tiling_grid(low, high, bins=(10, 10), offsets=(0.0, 0.0)):
return [np.linspace(low[dim], high[dim], bins[dim] + 1)[1:-1] + offsets[dim] for dim in range(len(bins))]
# 瓦片化
def create_tilings(low, high, tiling_specs):
return [create_tiling_grid(low, high, bins, offsets) for bins, offsets in tiling_specs]
'''
(3) Tile Encoding
'''
# 根据给定的网格离散样本。
def discretize(sample, grid):
return tuple(int(np.digitize(s, g)) for s, g in zip(sample, grid)) # 返回索引值
# 使用瓦片编码对给定的样本进行编码
def tile_encode(sample, tilings, flatten=False):
encoded_sample = [discretize(sample, grid) for grid in tilings] # 返回在相应瓦片上的坐标
return np.concatenate(encoded_sample) if flatten else encoded_sample
'''
(4) 使用瓦片编码的Q表
'''
class QTable:
# 初始化Q表
def __init__(self, state_size, action_size):
self.state_size = state_size
self.action_size = action_size
# Create Q-table, initialize all Q-values to zero
self.q_table = np.zeros(shape=(self.state_size + (self.action_size,)))
print("QTable(): size =", self.q_table.shape)
class TiledQTable:
"""组合q表与其内部的瓦片编码"""
# 瓦片化并初始化内部q表。
def __init__(self, low, high, tiling_specs, action_size):
self.tilings = create_tilings(low, high, tiling_specs)
self.state_sizes = [tuple(len(splits)+1 for splits in tiling_grid)
for tiling_grid in self.tilings] # 每片瓦片上的状态数
self.action_size = action_size
self.q_tables = [QTable(state_size, self.action_size)
for state_size in self.state_sizes] # 为每片瓦片建立一个q表
print("TiledQTable(): no. of internal tables = ", len(self.q_tables))
# 得到给定<状态,动作>对的q值。
def get(self, state, action):
# 获取在瓦片上的位置索引
encoded_state = tile_encode(state, self.tilings)
# 检索每片瓦片上的q值,并返回它们的平均值
value = 0.0
for idx, q_table in zip(encoded_state, self.q_tables): # 在每片瓦片上循环
value += q_table.q_table[tuple(idx + (action,))]
value = value / len(self.q_tables) # 计算平均值
return value
# 软更新q值为给定<状态,行动>对的值
def update(self, state, action, value, alpha=0.1):
# 获取在瓦片上的位置索引
encoded_state = tile_encode(state, self.tilings)
# 通过学习率alpha更新每个瓦片上的的q值
for idx, q_table in zip(encoded_state, self.q_tables):
value_ = q_table.q_table[tuple(idx + (action,))] # 获取当前位置q表的值
q_table.q_table[tuple(idx + (action,))] = alpha * value + (1.0 - alpha) * value_ # 使用学习率更新相关位置的值
'''
(5) Q学习智能体
'''
class QLearningAgent:
def __init__(self, env, tiled_q_table, alpha=0.02, gamma=0.99,
epsilon=1.0, epsilon_decay_rate=0.9995, min_epsilon=.01, seed=505):
"""初始化变量,创建离散化网格。"""
# Environment info
self.env = env
self.tq = tiled_q_table
self.state_sizes = tiled_q_table.state_sizes
self.action_size = self.env.action_space.n # 1-维离散动作空间
self.seed = np.random.seed(seed)
print("--Agent--\nEnvironment:", self.env)
print("State space size:", self.state_sizes)
print("Action space size:", self.action_size)
# 学习模型参数
self.alpha = alpha # 学习率
self.gamma = gamma # 折扣因子
self.epsilon = self.initial_epsilon = epsilon # 初始探索率
self.epsilon_decay_rate = epsilon_decay_rate # epsilon衰减系数
self.min_epsilon = min_epsilon
def reset_episode(self, state):
"""为新的事件重置变量."""
# 逐步降低探索率
self.epsilon *= self.epsilon_decay_rate
self.epsilon = max(self.epsilon, self.min_epsilon)
# 决定初始行动
self.last_state = state
Q_s = [self.tq.get(state, action) for action in range(self.action_size)]
self.last_action = np.argmax(Q_s)
return self.last_action
def reset_exploration(self, epsilon=None):
"""重置训练时使用的探索率."""
self.epsilon = epsilon if epsilon is not None else self.initial_epsilon
def act(self, state, reward=None, done=None, mode='train'):
"""选择next操作并更新内部Q表 (when mode != 'test')."""
Q_s = [self.tq.get(state, action) for action in range(self.action_size)]
greedy_action = np.argmax(Q_s)
if mode == 'test':
# 测试模式:简单地产生一个动作
action = greedy_action
else:
# 训练模式(默认):更新Q表,选择下一步行动
# Note: 我们用当前状态,回报更新最后的状态动作对的Q表条目
value = reward + self.gamma * max(Q_s)
self.tq.update(self.last_state, self.last_action, value, self.alpha)
# 探索 vs. 利用
do_exploration = np.random.uniform(0, 1) < self.epsilon
if do_exploration:
# 随机选择一个动作
action = np.random.randint(0, self.action_size)
else:
# 从Q表中选择最佳动作
action = greedy_action
# 存储当前状态,下一步操作
self.last_state = state
self.last_action = action
return action
'''
(6) 模型训练
'''
def run(agent, env, num_episodes=10000, mode='train'):
scores = []
max_avg_score = -np.inf
for i_episode in range(1, num_episodes+1):
# 初始化环境
state = env.reset()
action = agent.reset_episode(state)
total_reward = 0
done = False
while not done:
state, reward, done, info = env.step(action)
total_reward += reward
action = agent.act(state, reward, done, mode)
# 保存最终成绩
scores.append(total_reward)
if mode == "train":
if len(scores) > 100:
avg_score = np.mean(scores[-100:])
if avg_score > max_avg_score:
max_avg_score = avg_score
if i_episode % 100 == 0:
print("\rEpisode {}/{} | Max Average Score: {}".format(i_episode, num_episodes, max_avg_score), end="")
sys.stdout.flush()
return scores
# 主函数
if __name__ == "__main__":
# Set plotting options
plt.style.use('ggplot')
np.set_printoptions(precision=3, linewidth=120)
# Create an environment
env = gym.make('Acrobot-v1')
env.seed(505)
low = [-1.0, -5.0]
high = [1.0, 5.0]
test = create_tiling_grid(low, high, bins=(10, 10), offsets=(-0.1, 0.5))
# 设置分割精度
n_bins = 5
bins = tuple([n_bins] * env.observation_space.shape[0])
offset_pos = (env.observation_space.high - env.observation_space.low) / (3 * n_bins)
tiling_specs = [(bins, -offset_pos),
(bins, tuple([0.0] * env.observation_space.shape[0])),
(bins, offset_pos)]
tq = TiledQTable(env.observation_space.low,
env.observation_space.high,
tiling_specs,
env.action_space.n)
agent = QLearningAgent(env, tq)
scores = run(agent, env)
rolling_mean = plot_scores(scores)
'''
# 以下为相关测试代码
# Tiling specs: [(, ), ...]
tiling_specs = [((10, 10), (-0.066, -0.33)),
((10, 10), (0.0, 0.0)),
((10, 10), (0.066, 0.33))]
tilings = create_tilings(low, high, tiling_specs)
# visualize_tilings(tilings)
'''
'''
# Test with some sample values
samples = [(-1.2, -5.1),
(-0.75, 3.25),
(-0.5, 0.0),
(0.25, -1.9),
(0.15, -1.75),
(0.75, 2.5),
(0.7, -3.7),
(1.0, 5.0)]
encoded_samples = [tile_encode(sample, tilings) for sample in samples]
print("\nSamples:", repr(samples), sep="\n")
print("\nEncoded samples:", repr(encoded_samples), sep="\n")
# visualize_encoded_samples(samples, encoded_samples, tilings)
plt.show()
'''
'''
# Test with a sample Q-table
tq = TiledQTable(low, high, tiling_specs, 2)
s1 = 3;
s2 = 4;
a = 0;
q = 1.0
print("[GET] Q({}, {}) = {}".format(samples[s1], a,
tq.get(samples[s1], a))) # check value at sample = s1, action = a
print("[UPDATE] Q({}, {}) = {}".format(samples[s2], a, q));
tq.update(samples[s2], a, q) # update value for sample with some common tile(s)
print("[GET] Q({}, {}) = {}".format(samples[s1], a,
tq.get(samples[s1], a))) # check value again, should be slightly updated
'''
训练过程较慢,最后程序输出如下
Episode 10000/10000 | Max Average Score: -298.75