【深入浅出学习笔记】李沐《动手学深度学习2.0》之卷积神经网络基础
卷积神经网络基础 05.15-05.22
本文主要是学习李沐:动手学深度学习2.0在线课程的笔记。
视频地址:https://zhuanlan.zhihu.com/p/29125290。
教材全本:https://zh-v2.d2l.ai/
本课教材:https://zh-v2.d2l.ai/chapter_preliminaries/pandas.html
笔记地址:https://gitee.com/lhm8013609/mldl_-learning-notes.git
文章目录
- 卷积神经网络基础 05.15-05.22
-
- 1 从全连接层到卷积
-
- 1.1 神经网络设计的两个原则:
-
- 1.1.1 平移不变性:
- 1.1.2 局部性:
- 1.2 全连接层重新考察
-
- 1.2.1 v对w的重新索引,下标是如何对应的?
- 1.2.2 对全连接层使用平移不变性和局部性得到卷积层
-
- 1.2.2.1 平移不变性:
- 1.2.2.2 局部性:
- 1.2.2.3 总结
- 1.3 什么叫卷积?
- 1.4 小结
- 2 图像卷积
-
- 2.1 互相关运算
- 3 填充和步幅
-
- 3.1 概念
- 3.2 填充
- 3.3 步幅
- 4 多输入多输出通道
-
- 4.1 多个输入通道
- 4.2 多个输出通道
- 4.3 多个输入和输出通道
- 5 池化层
-
- 5.2 二维最大池化
- 5.3 填充、步幅、多个通道
- 5.4 平均池化层
- 5.5 小结
- 6 总结
1 从全连接层到卷积
1.1 神经网络设计的两个原则:
平移不变性、局部性
- 不能选取如位置这种思维固化的因素作为特征
- 只需要搜索图片局部区域
1.1.1 平移不变性:
不管出现在图像中的哪个位置,神经网络的底层应该对相同的图像区域做出类似的响应。这个原理即为“平移不变性”。
1.1.2 局部性:
神经网络的底层应该只探索输入图像中的局部区域,而不考虑图像远处区域的内容,这就是“局部性”原则。最终,这些局部特征可以融会贯通,在整个图像级别上做出预测。
1.2 全连接层重新考察
首先,假设以二维图像X为输入,那么我们多层感知机的隐藏表示H在数学上是一个矩阵,在代码中表示为二维张量。 其中X和H具有相同的形状。 我们可以认为,不仅输入有空间结构,隐藏表示也应该有空间结构。
- 将输入和输出变形为矩阵(宽度,高度)
- 将权重变形为4-D张量(h, w)到( h ′ h' h′, w ′ w' w′ )
- 之前是input到output的一个长度的变化
- 现在是input到output的一个宽、高的变化
1.2.1 v对w的重新索引,下标是如何对应的?
h i , j = ∑ k , l w i , j , k , l x k , l = ∑ a , b v i , j , a , b x i + a , j + b h_{i,j} = \sum_{k,l}w_{i,j,k,l}x_{k,l}=\sum_{a,b}v_{i,j,a,b}x_{i+a,j+b} hi,j=k,l∑wi,j,k,lxk,l=a,b∑vi,j,a,bxi+a,j+b
i , j i,j i,j是输出的宽高维度, k , l k,l k,l是输入的宽高维度;
对下标做一定的变化, k = i + a , l = j + b k=i+a,l=j+b k=i+a,l=j+b, v v v是 w w w的重新索引 v i , j , a , b = w i , j , i + a , j + b v_{i,j,a,b}=w_{i,j,i+a,j+b} vi,j,a,b=wi,j,i+a,j+b, 这里的索引a和b覆盖了正偏移和负偏移,对于隐藏表示中任意给定位置 ( i , j ) (i, j) (i,j)处的像素值 [ H ] i , j [H]_{i,j} [H]i,j,通过对x中以 ( i , j ) (i, j) (i,j)为中心的像素进行加权求和得到,权重为 v i , j , a , b v_{i,j,a,b} vi,j,a,b;
这个重新索引可以引出卷积的操作。
1.2.2 对全连接层使用平移不变性和局部性得到卷积层
1.2.2.1 平移不变性:
从公式(1)可以看出x的平移会导致h的平移;但从平移不变性来讲,v不应该依赖于 ( i , j ) (i,j) (i,j);
解决方案:去掉前两个维度, v i , j , a , b = v a , b v_{i,j,a,b}=v_{a,b} vi,j,a,b=va,b,则有:
h i , j = ∑ a , b v a , b x i + a , j + b h_{i,j} = \sum_{a,b}v_{a,b}x_{i+a,j+b} hi,j=a,b∑va,bxi+a,j+b
这就是2维卷积,实际上在数学上叫2维的交叉相关。
实际上,我们是在使用系数 [ V ] a , b [V]_{a,b} [V]a,b对位置 ( i , j ) (i,j) (i,j)附近的像素$ (i+a,j+b) 进行加权求和来得到 进行加权求和来得到 进行加权求和来得到[H]{i,j} 。注意, 。 注意, 。注意,[V]{a,b} 的参数比 的参数比 的参数比[V]_{i,j,a,b}$少很多,因为前者不再依赖于图像中的位置。
二维卷积就是全连接或者矩阵乘法,但是权重使得一些东西是重复的,不是每一个元素都可以自由变换;当我把一个模型的取值做了限制,模型的复杂度就会降低,以为元素存量减小。(卷积就是weight shared全连接?)
1.2.2.2 局部性:
- 当评估 h i , j h_{i,j} hi,j时,我们应该只考虑输入 x i , j x_{i,j} xi,j附近的参数
- 解决方案:当 ∣ a ∣ , ∣ b ∣ > Δ |a|,|b|>\Delta ∣a∣,∣b∣>Δ时,使得 v a , b = 0 v_{a,b}=0 va,b=0
h i , j = ∑ a = − Δ Δ ∑ b = − Δ Δ v a , b x i + a , j + b h_{i,j}=\sum^{\Delta}_{a=-\Delta}\sum^{\Delta}_{b=-\Delta}v_{a,b}x_{i+a,j+b} hi,j=a=−Δ∑Δb=−Δ∑Δva,bxi+a,j+b
a,b只在 − Δ -\Delta −Δ到 Δ \Delta Δ变化。
公式(3)是一个卷积层(convolutional layer),而卷积神经网络是包含卷积层的一类特殊的神经网络。 在深度学习研究社区中,$ V $被称为 卷积核 (convolution kernel) 或者 滤波器 (filter),是可学习的权重。
1.2.2.3 总结
对全连接层使用平移不变性和局部性得到卷积层,主要是压缩了两个维度以及限制了a,b的取值范围。
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ZlNCoK3Y-1665580420184)(images/lhm/image-20210712135155826.png)]
1.3 什么叫卷积?
- 数学中的卷积定义
( f ∗ g ) ( x ) = ∫ f ( z ) g ( x − z ) d z (f*g)(x)= \int f(z)g(x-z)dz (f∗g)(x)=∫f(z)g(x−z)dz
也就是说,卷积是测量 f f f和 g g g之间(把其中一个函数“翻转”并移位x时)的重叠.
- 当我们有离散对象时(即定义域为 Z Z Z),积分就变成求和,我们得到以下定义:
( f ∗ g ) ( i ) = ∑ a f ( a ) g ( i − a ) (f*g)(i)= \sum_a f(a)g(i-a) (f∗g)(i)=a∑f(a)g(i−a)
- 对于二维张量,则为 f f f在 ( a , b ) (a,b) (a,b)和 g g g在 ( i − a , j − b ) (i−a,j−b) (i−a,j−b)上的对应和:
( f ∗ g ) ( i , j ) = ∑ a ∑ b f ( a , b ) g ( i − a , j − b ) (f*g)(i,j)= \sum_a\sum_b f(a,b)g(i-a,j-b) (f∗g)(i,j)=a∑b∑f(a,b)g(i−a,j−b)
这里使用差值,而不是和,实际上可以化简为一致的。
1.4 小结
- 图像的平移不变性使我们可以以相同的方式处理局部图像。就是使用相同的卷积核,也即是权重相同,所以才叫weight shared全连接,权重共享。
- 局部性意味着计算相应的隐藏表示只需一小部分局部图像像素。
- 在图像处理中,卷积层通常比全连接层需要更少的参数。
- 卷积神经网络(CNN)是一类特殊的神经网络,它可以包含多个卷积层。
- 多个输入和输出通道使模型在每个空间位置可以获取图像的多方面特征。
2 图像卷积
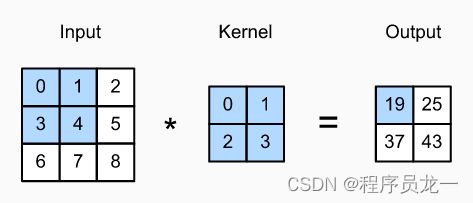
2.1 互相关运算
输入是高度为3 、宽度为3的二维张量(即形状为3×3)。卷积核的高度和宽度都是2,而卷积核窗口(或卷积窗口)的形状由内核的高度和宽度决定(即2×2)。
3 填充和步幅
3.1 概念
填充:在输入周围添加额外的行/列
步幅:步幅是指行/列的滑动步长
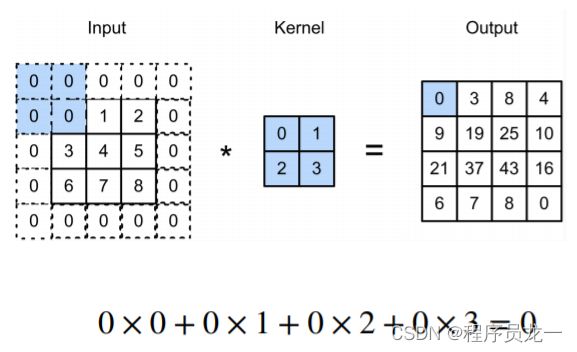
3.2 填充
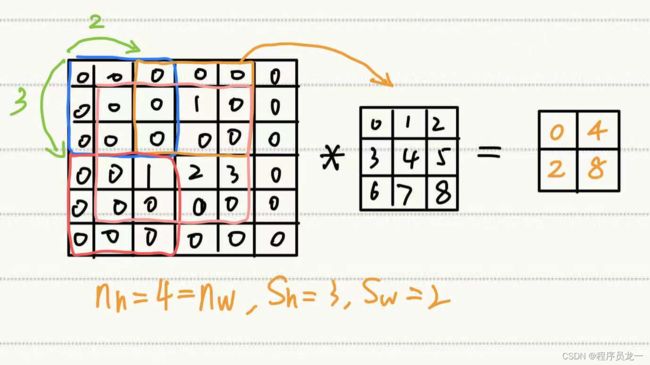
- 如果填充 p h p_h ph行和 p w p_w pw列,输出形状为: ( n h − k h + p h + 1 ) × ( n w − k w + p w + 1 ) (n_h-k_h+p_h+1)×(n_w-k_w+p_w+1) (nh−kh+ph+1)×(nw−kw+pw+1)
- 通常取 p h = k h − 1 , p w = k w − 1 p_h=k_h-1,p_w=k_w-1 ph=kh−1,pw=kw−1
- 当 k h k_h kh为奇数时:在上下两侧填充 p h / 2 p_h/2 ph/2,如3*3的卷积核,则上下两侧各填充1行、1列
- 当 k h k_h kh为偶数时, p h p_h ph为奇数,在上侧填充 p h / 2 p_h/2 ph/2,,上侧多1行;在下侧填充 p h / 2 p_h/2 ph/2,下侧少1行;如4*4的卷积核,上侧填充3/2=1+1=2行,下侧1行
3.3 步幅
4 多输入多输出通道
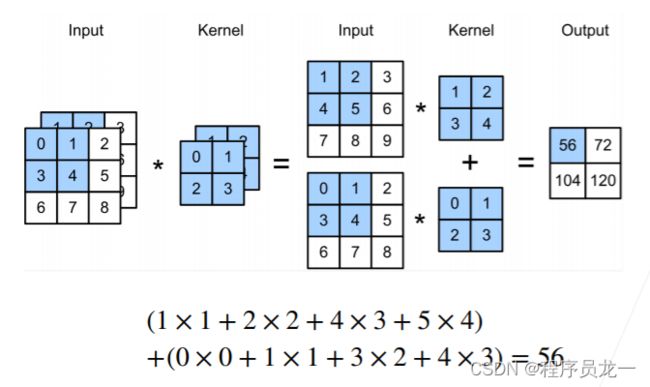
4.1 多个输入通道
- 每个通道都有一个卷积核,结果是所有通道卷积结果的和
4.2 多个输出通道
4.3 多个输入和输出通道
5 池化层
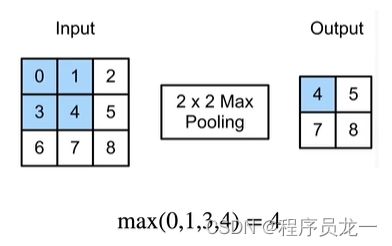
5.2 二维最大池化
- 返回滑动窗口中的最大值
5.3 填充、步幅、多个通道
- 填充为1、步幅为2
- 没有可学习的参数kernel
- 每个通道做池化层然后获得相应输出通道
- 输出通道数=输入通道数
5.4 平均池化层
- 最大池化层:每个窗口中最强的模式信号
- 平均池化层:将最大池化层中的“最大值”替换为“平均值”
5.5 小结
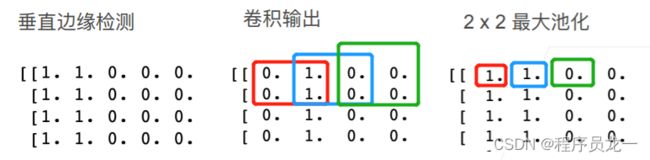
- 池化层返回窗口中最大或平均值
- 缓解卷积层对位置的敏感性
- 同样有窗口大小、填充、和步幅作为超参数
6 总结
-
超参数:核大小、填充、步幅影响重要程度
- 核大小最重要,填充默认、步幅取决于特征提取的模型复杂度控制
-
卷积核边长取奇数,填充后对称
-
卷积核大小一般不自己设计,采用经典网络结构居多,如,ResNet,只进行微调
-
超参数如何参加训练?NAS(Neural Network Architecture Search)
-
自动调参神经网络,autogluon
-
卷积核越小,计算速度越快;如3*3会比5*5的更快,虽然从效果上说两者在多层卷积上可以替换
【龙一的编程life】该公z号主要用于分享人工智能、嵌入式等相关学习笔记以及项目,包括但不限于Python、C/C++、DL、ML、CV、ARM、Linux等相关技术;分享资源,一起学习一起happy!