AI作业4-无监督学习

K均值聚类 （K-means）

聚类

首先我们回顾下：聚类任务为将数据集中的样本划分为若干个通常是不相交的子集中，这些子集称为样本簇

k均值聚类（k-means clustering algorithm）

• k均值聚类是一种迭代求解的聚类分析算法，是最基础和最常用的聚类算法之一（无监督学习），它将数据集中某些相似地方的数据特征进行分组、组织的过程。首先先将数据分为K组，然后随机选取K个对象作为初始的聚类中心，然后计算每个对象与各个种子聚类中心之间的距离，把每个对象分配给距离它最近的聚类中心。其基本思想是通过迭代方式寻找K个簇(Cluster）的一种划分方案，使得聚类结果对应的代价函数最小。

算法步骤：

# 伪代码
function K-Means(输入数据，中心点个数K)
    获取输入数据的维度Dim和个数N
    随机生成K个Dim维的点
    while(算法未收敛)
        对N个点：计算每个点属于哪一类。
        对于K个中心点：
            1，找出所有属于自己这一类的所有数据点
            2，把自己的坐标修改为这些数据点的中心点坐标
    end
    输出结果：
end

(可)参考链接：
k-means法を理解する
非监督学习： K 均值聚类（原理、步骤、优缺点、调优）
聚类方法：k均值聚类、层次聚类
sklearn（六）-K-Means k均值聚类算法
机器学习十大经典算法之K-Means聚类算法

K均值聚类是生成式还是判别式方法？

回顾：生成式方法是指通过学习样本数据的分布，来得到联合概率分布P(X,Y)，然后求出条件概率分布P(Y|X)。判别式方法是指直接学习决策函数f(X)，或者条件概率分布P(Y|X)，从而得到对输入X的输出Y。
简单来说判别式模型则是直接建立一个输入和输出之间的映射关系，它的目的是寻找一个决策边界来区分不同的数据。

Obviously， K均值聚类是一种判别式方法，它通过将数据分为K个簇来进行聚类，区分的边界就是这些类簇距离中心的距离所形成的“边界”。

KNN VS. K-means

回顾KNN & K-means：

• K-means 参见上文
• KNN：k近邻法（k-nearest neighbor，k-NN）是一种基本的分类和回归方法，是监督学习方法里的一种常用方法。k近邻算法假设给定一个训练数据集，其中的实例类别已定。分类时，对新的实例，根据其k个最近邻的训练实例类别，通过多数表决等方式进行预测。即（物以类聚，人以群分）

区别

1. K-means是聚类算法；KNN是分类算法。
2. K-means是无监督学习（样本没有标签）；KNN是监督学习（一部分样本要有标签）。
3. Kmeans中的K，表示分成K簇；KNN中的K，表示寻找与测试数据最近的K个样本。
4. Kmeans有明显的前期训练过程；KNN没有明显的前期训练过程。
5. Kmeans对异常值敏感，KNN对异常值不敏感
6. Kmeans可以进行多分类，KNN样本只能归为一类，不适合多分类任务；

(可)参考链接：//从KNN & K-means 的优缺点中我们就可以很容易的看出两者的区别
KNN和Kmeans比较
机器学习：KNN原理及其改进
【机器学习】K-means（非常详细）

主成分分析（PCA）

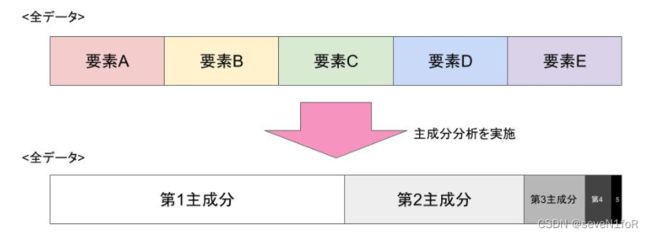
主成分分析（PCA，Principal Component Analysis）是一种使用最广泛的数据降维算法。它是一种统计学方法，用于将多个相关变量压缩为少数几个无关变量，称为主成分，以便更好地解释数据。PCA是一种无监督学习方法，因为它不需要任何关于数据的先验知识或标签。主成分分析的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。

用处：PCA可以用于多种应用程序，例如图像处理、模式识别、数据压缩和信号处理。在图像处理中，PCA可用于减少图像中的噪声和增强图像中的特定特征。在模式识别中，主成分分析可用于识别数据集中的模式和类别。在数据压缩中，主成分分析可用于减少数据集的大小，并提高计算效率。在信号处理中，主成分分析可用于提取信号中的重要信息，并减少噪声和干扰。

(可)参考链接：

主成分分析とは? 例を使って活用方法とメリットをわかりやすく解説
【主成分分析是什么？使用例子简单的理解使用方法】（NTT日本语文章有阅读门槛）

主成分分析（PCA）原理详解

LDA VS. PCA

LDA（线性判别分析）回顾：**最大化类间均值，最小化类内方差。**将数据投影在低维度上，并且投影后同类别别数据的投影点尽可能的接近，不同类别数据的投影点的中心点尽可能的远。

二者区别：

1. LDA是监督学习的方法，PCA是无监督学习的方法
2. 如上文所述LDA最大化类间均值，最小化类内方差；PCA将高维数据投影到低维空间中，同时保持最大方差。
3. LDA考虑了类别信息，在降维过程中尽可能提高不同类别之间的可分性；
4. PCA只考虑数据的方差，通过保留数据中最主要的特征或方向，将数据投影到低维空间中
5. LDA也常用于分类问题的特征提取，PCA则更常用于数据可视化和去噪。

(可)参考链接：
上期博客：AI作业2-监督学习

奇异值分解（SVD）

回顾特征值和特征向量

• 特征值（eigenvalue）是一个数，是方阵矩阵与一个非零向量相乘的结果，其结果是这个向量的线性倍数，即原向量在这个矩阵的变换下的放缩因子。如果一个矩阵 A 有特征值 λ，那么对应的特征向量（eigenvector）v 就满足 Av = λv，其中 v 是非零向量。也就是说，对于矩阵 A 和特征向量 v，矩阵 A 对向量 v 进行的线性变换只是对 v 进行了伸缩，并没有改变其方向。
• 特征向量（eigenvector）是指在进行线性变换时，其方向不发生变化的向量。特征向量可以看作是在变换中保持不变的方向，而特征值则表示这个方向上的放缩因子。特征向量可以通过求解矩阵 A 减去 λI（其中 I 为单位矩阵）的行列式等于 0 的方程组得到，其中 λ 是 A 的特征值。

奇异值分解（SVD）

• 奇异值分解(Singular Value Decomposition，以下简称SVD)是在机器学习领域广泛应用的算法，它不光可以用于降维算法中的特征分解，还可以用于推荐系统，以及自然语言处理等领域。是很多机器学习算法的基石。
• SVD是一种线性代数的方法，用于将一个矩阵分解成三个矩阵的乘积的形式，即 $A=U\Sigma V^T$，其中 $A$ 是一个 $m\times n$ 的实数矩阵，$U$ 和 $V$ 是两个正交矩阵，$\Sigma$ 是一个 $m\times n$ 的对角矩阵，其对角线上的元素称为奇异值。

• 优点:是能够处理各种形状和大小的矩阵，并且可以捕捉数据集的主要特征。它还可以通过保留前 $k$ 个奇异值，对矩阵进行压缩，减少存储空间和计算成本。
• 缺点:对于大型矩阵，SVD 的计算成本较高，可能需要很长时间才能完成计算。此外，在实践中，SVD 的输出通常是稠密的，因此对于大型稀疏矩阵，可能需要使用其他方法。

(可)参考链接：
奇异值分解（SVD）

SVD使用场景见下↓

特征人脸方法（Eigenface）

特征人脸方法（Eigenface）是一种用于人脸识别的计算机视觉问题的方法，它利用了一组特征向量来表示人脸。这种方法是由 Sirovich 和 Kirby 提出的，并由 Turk 和 Pentland 用于人脸分类。特征向量是从人脸图像的协方差矩阵中求出的，再从中捕捉人脸的主要变化。

PCA 的几何解释

1. 找到一组新的坐标轴，或者说是一组新的基（basis），用于表示原来的数据，使得在表示数据时不同轴是不相关的（即协方差为0）。
2. 取出其中含有信息较多（即方差较大）的坐标轴（基），构成（span）一个新的空间，舍弃其他维度的信息。
3. 由于新空间的维度小于原来的空间，所以把数据投影到新的空间后，可以大大降低数据的复杂度（虽然会损失少量信息）。

PCA 的大致思路PCA 的大致思路

• 样本中心化：算出数据在每一个维度上的平均值，让该维数值减去这个平均值，中心化不会改变求得的新空间，但会减少计算量。
• 对中心化后的数据，算出这些数据的协方差矩阵。协方差矩阵的含义：第 i 行 k 列的值，表示 i k 对应的两个方向（坐标轴）的协方差。
• 对协方差矩阵进行对角化，即算出协方差矩阵的特征值与特征向量。
  含义：对角化意味着非对角线元素为0，也就意味着不同坐标轴（不同方向）之间两两互不相关（协方差为0）。而协方差矩阵对角线上元素，就是数据在各个方向上的方差（也是特征值），方差越大意味着数据在这个方向上的散度越大，也就意味着这个方向包含的信息更多。
• 取特征值大的一些特征向量构成一个矩阵 P，这个矩阵是一个投影矩阵：能够把原始空间的数据投影到新的空间。

(可)参考链接：
基于 PCA 的人脸识别方法——特征脸法[1]

潜在语义分析 (LSA)

潜在语义分析（Latent Semantic Analysis，LSA）是一种自然语言处理技术，属于分布式语义学的范畴，它通过生成一组与文档和词语相关的概念，来分析一组文档和它们包含的词语之间的关系。LSA 假设意思相近的词语会出现在相似的文本片段中，因此可以通过统计词语在文档中的共现情况，来推断词语之间的语义相似度。

• 当生成了词汇－文档矩阵后，LSA提供了一种对它的低维近似（可以通过对字词—文档矩阵的奇异值分解（SVD）来实现）。做这种近似有以下几种原因：

1. 对原始的词汇-文档矩阵进行计算时，计算量太大。而低维矩阵提供了一种近似（尽量少但却不可避免地有一些信息丢失）。
2. 原始的矩阵一般包含噪声（垃圾信息）。在这种意义上，近似的低维矩阵是一种去噪矩阵（比原始矩阵更好）。
3. 原始的词汇－文档矩阵过度地稀疏。它罗列了每篇文档中的实际出现的词汇，而由于同义词的存在，我们关心的是所有地与文档有关系的词汇集合，这个集合一般要比实际出现的词汇集合要大得多。

(可)参考链接：
LSA潜在语义分析的原理、公式推导和应用
wiki——潜在语义学

期望最大化算法（EM）

期望最大化算法（Expectation-Maximization，EM）是一种迭代算法，用于含有隐变量（Hidden Variable）的概率参数模型的最大似然估计或极大后验概率估计。
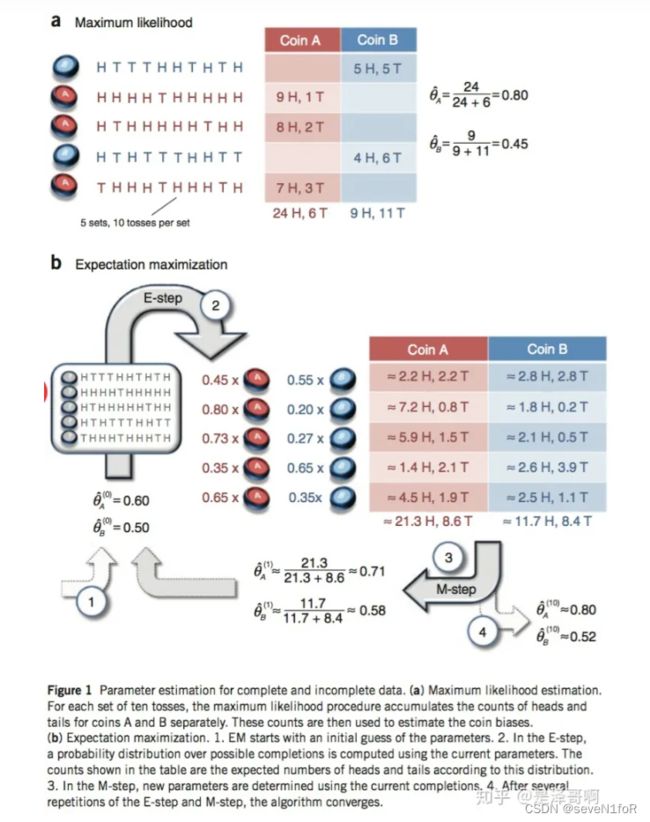
EM算法的基本思想是：在每次迭代中，先根据当前的参数估计值计算隐变量的期望值（E步），然后根据期望值最大化参数的对数似然函数（M步），重复这个过程直到收敛。如下图(下称 图_EM )：

EM算法的步骤

• EM算法的优点有：
  它可以有效地处理含有隐变量的复杂模型，如高斯混合模型、隐马尔可夫模型等。
  它可以保证每次迭代都不会降低似然函数的值，即具有单调递增性。
  它可以利用局部信息进行参数更新，而不需要全局信息，因此可以节省计算资源。
• EM算法的缺点有：
  它需要指定初始参数值，而这些值可能会影响算法的收敛速度和结果。
  它可能会陷入局部最优解，而不是全局最优解。即可能会收敛到一个奇异点（singular point），即似然函数的极限值，而不是最大值。

(可)参考链接：
EM算法及其推广
【机器学习】EM——期望最大（非常详细）
EM算法详解
什么是 EM 算法（最大期望算法）？【知多少】

K-means是最简单的EM算法？

不完全正确。K-means算法是一种特殊的EM算法，它可以看作是对高斯混合模型（Gaussian Mixture Model，GMM）的简化。K-means算法假设每个类别的协方差矩阵是单位矩阵，即每个类别的数据分布是各向同性的（isotropic），并且每个类别的先验概率相等。在这些假设下，K-means算法的E步和M步可以简化为：

• E步：根据当前的类别中心，将每个数据点分配到距离最近的类别中。
• M步：根据当前的数据点分配，更新每个类别的中心为该类别数据点的均值。

因此，K-means算法可以看作是EM算法的一种特例，但不是最简单的EM算法。

编程实现EM算法

源码-参考链接：数据为 图_EM 的硬币抛掷结果

# -*- coding: utf-8 -*-
# @File    : EMAlgorithm.py
# @Time    : 2023/4/8 18:59
# @Author  : seveN1foR
# @Version : 1.0
# @Software: PyCharm 
# @Contact : [email protected]

# here put the import lib
import numpy as np
from scipy import stats

# 硬币投掷结果观测序列
observations = np.array([[1, 0, 0, 0, 1, 1, 0, 1, 0, 1],
                         [1, 1, 1, 1, 0, 1, 1, 1, 1, 1],
                         [1, 0, 1, 1, 1, 1, 1, 0, 1, 1],
                         [1, 0, 1, 0, 0, 0, 1, 1, 0, 0],
                         [0, 1, 1, 1, 0, 1, 1, 1, 0, 1]])


def em_single(priors, observations):
    """
    EM算法单次迭代
    Arguments
    ---------
    priors : [theta_A, theta_B]
    observations : [m X n matrix]

    Returns
    --------
    new_priors: [new_theta_A, new_theta_B]
    :param priors:
    :param observations:
    :return:
    """
    counts = {'A': {'H': 0, 'T': 0}, 'B': {'H': 0, 'T': 0}}
    theta_A = priors[0]
    theta_B = priors[1]
    # E step
    for observation in observations:
        len_observation = len(observation)
        num_heads = observation.sum()
        num_tails = len_observation - num_heads
        contribution_A = stats.binom.pmf(num_heads, len_observation, theta_A)
        contribution_B = stats.binom.pmf(num_heads, len_observation, theta_B)  # 两个二项分布
        weight_A = contribution_A / (contribution_A + contribution_B)
        weight_B = contribution_B / (contribution_A + contribution_B)
        # 更新在当前参数下A、B硬币产生的正反面次数
        counts['A']['H'] += weight_A * num_heads
        counts['A']['T'] += weight_A * num_tails
        counts['B']['H'] += weight_B * num_heads
        counts['B']['T'] += weight_B * num_tails
    # M step
    new_theta_A = counts['A']['H'] / (counts['A']['H'] + counts['A']['T'])
    new_theta_B = counts['B']['H'] / (counts['B']['H'] + counts['B']['T'])
    return [new_theta_A, new_theta_B]


def em(observations, prior, tol=1e-6, iterations=10000):
    """
    EM算法
    :param observations: 观测数据
    :param prior: 模型初值
    :param tol: 迭代结束阈值
    :param iterations: 最大迭代次数
    :return: 局部最优的模型参数
    """
    iteration = 0
    while iteration < iterations:
        new_prior = em_single(prior, observations)
        delta_change = np.abs(prior[0] - new_prior[0])
        if delta_change < tol:
            break
        else:
            prior = new_prior
            iteration += 1
    return [new_prior, iteration]


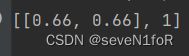
print(em(observations, [0.6, 0.5]))

• 运行结果：
  
  对其中的数据稍作修改
  
  结果：
  
  两者相等的情况下会出现问题：
  
  
  可见，这里只迭代了一次，且只要两者相同时便会出现这样的情况。
  提高释放阈值：

tol=1e-12，//迭代结束阈值

可见，迭代次数增长，且数据的位数更多了。