AI作业6-误差反向传播
梯度下降
- 梯度下降法是机器学习中常用的一种算法，它虽然不是机器学习算法本身，但是却是一种非常重要的最优化算法。它的主要作用是寻找最小值，基本思想就是一步步地接近最好的点，每一步都朝着梯度的方向优化。
- 机器学习的核心就是让模型通过不断学习数据来提升自己，而这个学习过程就是通过梯度下降法不断优化的过程。现在最常见的深度神经网络就是利用梯度的反向传播（Backpropagation）方法，通过反复更新模型参数直到收敛，以达到优化模型的目的。
- 常见的梯度下降法包括随机梯度下降法（SGD）、批梯度下降法、Momentum梯度下降法、Nesterov Momentum梯度下降法、AdaGrad梯度下降法、RMSprop梯度下降法和Adam梯度下降法。这些方法在不同场景下有各自的优势和适用性。
(可)参考链接：
详解梯度下降法（干货篇）
（十七）通俗易懂理解——梯度下降算法
反向传播 (Backpropagation，BP)
反向传播（Backpropagation）是一种训练人工神经网络的常见方法，它利用梯度下降法或其他优化方法来最小化损失函数。下面是反向传播的具体步骤：
- 正向传播（Forward Propagation）：输入数据通过网络的各层，得到输出结果和损失值。
- 反向传播（Backward Propagation）：
- 从最后一层开始，计算每一层的误差（Error），误差的计算是从后往前推进的。
- 使用链式法则，计算每个参数的偏导数（Gradient）。
- 计算梯度（Gradient Calculation）：根据偏导数计算每个神经元连接权重的梯度。
- 更新参数（Parameter Update）：根据梯度下降法则，利用计算得到的梯度更新参数，目标是使损失函数的值逐渐减小。
- 重复步骤 1-4：迭代以上步骤，直到满足停止准则，比如相邻两次迭代的误差的差别很小。
通过不断迭代上述步骤，神经网络能够学习并调整参数，以实现对输入数据的准确预测和分类。反向传播是一种基于梯度的优化方法，它在机器学习和深度学习中扮演着重要的角色。
注：详细过程查阅参考链接
(可)参考链接：
解读反向传播算法（图与公式结合）
计算图
计算图是一种用来描述运算的有向无环图。计算图有两个主要元素：结点（Node）和边（Edge）。结点表示数学运算，边表示运算之间的数据流。计算图可以用来表达和评估数学表达式，也可以用来实现深度学习框架中的反向传播算法。
计算图被定义为有向图，其中节点对应于数学运算。计算图是表达和评估数学表达式的一种方式。
例如，这里有一个简单的数学公式:
a = (b + c) * (d - e)
可以使用计算图来表示该公式。在计算图中，每个节点表示一个数学运算，例如加法、减法和乘法。节点之间的边表示运算之间的依赖关系。
b ----
\
[ + ]
/ \
c ---- \
\
[ * ]
/ \
d ---- / \
\ / \
[ - ] e
/ \
在这个计算图中，节点b和节点c表示输入变量，节点+表示加法运算，节点-表示减法运算，节点*表示乘法运算。计算图的顺序是从左到右，从上到下。通过沿着计算图的路径进行计算，可以得到最终的结果。
计算图的优势在于它能够将复杂的数学表达式分解成简单的计算步骤，并通过反向传播算法有效地计算梯度，从而用于训练神经网络等机器学习任务中。
(可)参考链接：
计算图
使用Numpy编程实现例题
题目
输入值：x1, x2 = 0.5，0.3
输出值：y1, y2 =0.23， -0.07
激活函数：sigmoid
损失函数：均方误差（Mean Squared Error，MSE）
初始权值：0.2 -0.4 0.5 0.6 0.1 -0.5 -0.3 0.8
目标：通过反向传播优化权值
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(z):
a = 1 / (1 + np.exp(-z))
return a
def forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8): # 正向传播
in_h1 = w1 * x1 + w3 * x2
out_h1 = sigmoid(in_h1)
in_h2 = w2 * x1 + w4 * x2
out_h2 = sigmoid(in_h2)
in_o1 = w5 * out_h1 + w7 * out_h2
out_o1 = sigmoid(in_o1)
in_o2 = w6 * out_h1 + w8 * out_h2
out_o2 = sigmoid(in_o2)
error = (1 / 2) * (out_o1 - y1) ** 2 + (1 / 2) * (out_o2 - y2) ** 2
return out_o1, out_o2, out_h1, out_h2, error
def back_propagate(out_o1, out_o2, out_h1, out_h2): # 反向传播
d_o1 = out_o1 - y1
d_o2 = out_o2 - y2
d_w5 = d_o1 * out_o1 * (1 - out_o1) * out_h1
d_w7 = d_o1 * out_o1 * (1 - out_o1) * out_h2
d_w6 = d_o2 * out_o2 * (1 - out_o2) * out_h1
d_w8 = d_o2 * out_o2 * (1 - out_o2) * out_h2
d_w1 = (d_w5 + d_w6) * out_h1 * (1 - out_h1) * x1
d_w3 = (d_w5 + d_w6) * out_h1 * (1 - out_h1) * x2
d_w2 = (d_w7 + d_w8) * out_h2 * (1 - out_h2) * x1
d_w4 = (d_w7 + d_w8) * out_h2 * (1 - out_h2) * x2
return d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8
def update_w(step, w1, w2, w3, w4, w5, w6, w7, w8): # 梯度下降，更新权值
w1 = w1 - step * d_w1
w2 = w2 - step * d_w2
w3 = w3 - step * d_w3
w4 = w4 - step * d_w4
w5 = w5 - step * d_w5
w6 = w6 - step * d_w6
w7 = w7 - step * d_w7
w8 = w8 - step * d_w8
return w1, w2, w3, w4, w5, w6, w7, w8
if __name__ == "__main__":
w1, w2, w3, w4, w5, w6, w7, w8 = 0.2, -0.4, 0.5, 0.6, 0.1, -0.5, -0.3, 0.8 # 可以给随机值，为配合PPT，给的指定值
x1, x2 = 0.5, 0.3 # 输入值
y1, y2 = 0.23, -0.07 # 正数可以准确收敛；负数不行。why? 因为用sigmoid输出，y1, y2 在 （0,1）范围内。
N = 10 # 迭代次数
step = 10 # 步长
print("输入值：x1, x2；", x1, x2, "输出值：y1, y2:", y1, y2)
eli = []
lli = []
for i in range(N):
print("=====第" + str(i) + "轮=====")
# 正向传播
out_o1, out_o2, out_h1, out_h2, error = forward_propagate(x1, x2, y1, y2, w1, w2, w3, w4, w5, w6, w7, w8)
print("正向传播:", round(out_o1, 5), round(out_o2, 5))
print("损失函数：", round(error, 2))
# 反向传播
d_w1, d_w2, d_w3, d_w4, d_w5, d_w6, d_w7, d_w8 = back_propagate(out_o1, out_o2, out_h1, out_h2)
# 梯度下降，更新权值
w1, w2, w3, w4, w5, w6, w7, w8 = update_w(step, w1, w2, w3, w4, w5, w6, w7, w8)
eli.append(i)
lli.append(error)
plt.plot(eli, lli)
plt.ylabel('Loss')
plt.xlabel('w')
plt.show()
运行
运行——修改
N = 100 # 迭代次数
step = 1 # 步长
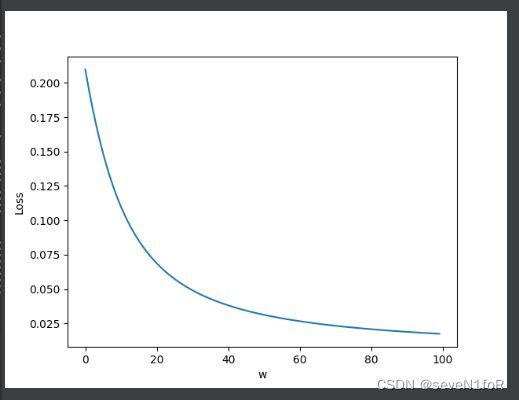>可见曲线变的更加圆滑
step = 20 # 步长
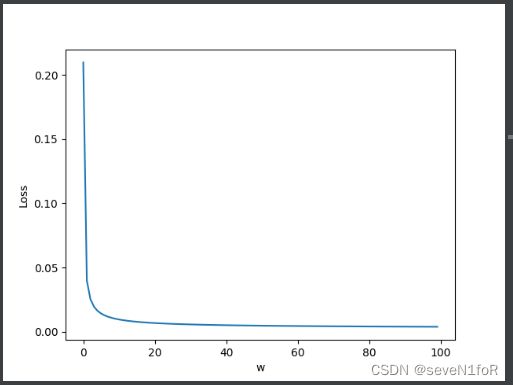
步子太大
N = 10 # 迭代次数
step = 5 # 步长
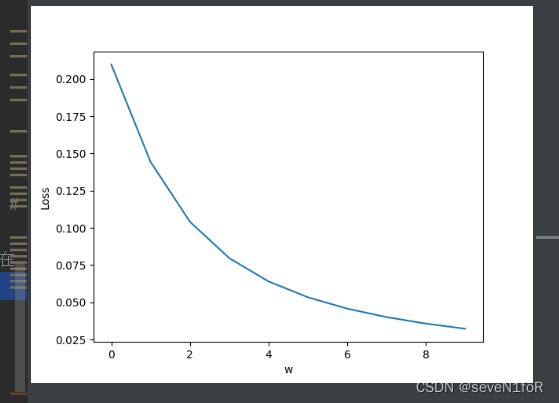
迭代次数不足造成的欠拟合
原文中便是通过调整迭代次数和步长，通过损失函数-均方误差的反馈来调整，并得出较优超参数。
(可)参考链接：
【人工智能导论：模型与算法】MOOC 8.3 误差后向传播(BP) 例题 编程验证「源码地址」
使用PyTorch的Backward（）编程实现例题
要使用 PyTorch 实现上述代码中的反向传播过程，您需要将输入和权重转换为 PyTorch 的张量，并利用 PyTorch 的自动微分功能来计算梯度和更新权重
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
def sigmoid(z):
a = 1 / (1 + torch.exp(-z))
return a
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# 权重
self.w1 = nn.Parameter(torch.tensor(0.2))
self.w2 = nn.Parameter(torch.tensor(-0.4))
self.w3 = nn.Parameter(torch.tensor(0.5))
self.w4 = nn.Parameter(torch.tensor(0.6))
self.w5 = nn.Parameter(torch.tensor(0.1))
self.w6 = nn.Parameter(torch.tensor(-0.5))
self.w7 = nn.Parameter(torch.tensor(-0.3))
self.w8 = nn.Parameter(torch.tensor(0.8))
def forward(self, x1, x2, y1, y2):
in_h1 = self.w1 * x1 + self.w3 * x2 # 输入到隐藏层神经元 h1 的加权和
out_h1 = sigmoid(in_h1) # 隐藏层神经元 h1 的输出
#下面的同理
in_h2 = self.w2 * x1 + self.w4 * x2
out_h2 = sigmoid(in_h2)
in_o1 = self.w5 * out_h1 + self.w7 * out_h2
out_o1 = sigmoid(in_o1)
in_o2 = self.w6 * out_h1 + self.w8 * out_h2
out_o2 = sigmoid(in_o2)
error = (1 / 2) * (out_o1 - y1) ** 2 + (1 / 2) * (out_o2 - y2) ** 2
return out_o1, out_o2, out_h1, out_h2, error
def main():
x1, x2 = 0.5, 0.3 # 输入值
y1, y2 = 0.23, -0.07 # 输出值
N = 10 # 迭代次数
step = 10 # 步长
print("输入值：x1, x2；", x1, x2, "输出值：y1, y2:", y1, y2)
eli = [] # 存储每一轮迭代的迭代次数
lli = [] # 存储每一轮迭代的损失值
model = Net()
optimizer = torch.optim.SGD(model.parameters(), lr=step)
for i in range(N):
optimizer.zero_grad()
out_o1, out_o2, out_h1, out_h2, error = model(x1, x2, y1, y2)
print("=====第" + str(i) + "轮=====")
print("正向传播:", round(out_o1.item(), 5), round(out_o2.item(), 5))
print("损失函数：", round(error.item(), 2))
error.backward()# 反向传播，计算梯度
optimizer.step()# 更新权重
eli.append(i)
lli.append(error.item())
plt.plot(eli, lli)
plt.ylabel('Loss')
plt.xlabel('Iteration')
plt.show()
if __name__ == "__main__":
main()
这里直接引用例题的较优解
(可)参考链接：
pytorch安装参考
注：本人使用的是NV的GameReady驱动，自带cuDNN和CUDA
将Anaconda设置为国内镜像源的方法
Anaconda安装-超详细版(2023)