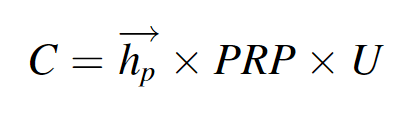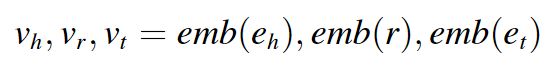论文浅尝 | PANC:知识图谱中的原型扩展邻域约束实体补全
笔记整理:付可意,天津大学硕士
链接:https://doi.org/10.1016/j.eswa.2022.119013
动机
知识图谱(Knowledge graph, KGs)以事实三元组的形式收集和存储大量的常识或领域知识,事实三元组以(头实体、关系实体、尾实体)的形式表示。近年来,许多现有的知识图谱,如Freebase, YAGO, NELL,已被视为关键资源,并被引入许多人工智能应用,如问答、推荐和语义搜索。然而,它们通常是不完整的,并且仍然存在实体之间关系缺失的问题。然而,绝大多数方法通常将KG补全任务定义为链接预测任务。具体来说,给定事实三元组中的两个元素,任务是推断缺失的元素,例如(h, r, ?), (h, ?, t), (?, r, t),其中问号代表缺失的实体/关系。虽然这样的任务已经取得了优异的成绩,但是在很多情况下仍然是不合理的,比如对(Trump, capital of, ?)的预测。链接预测任务隐含地假设给定的两个元素是强相关的。现有的大多数作品都是通过在KG中从真三元组中取出一个元素来实现的,从而保证了假设。然而,在现实世界中,我们通常不会得到两个相关的元素,因此经常会出现(Trump,capital of,?)这样无意义的组合。对于这种本质上没有意义的组合,无论最终的推理结果是什么,形成的三元组都没有意义。因此,我们需要更合理的方法,尽可能的去除这些无效的组合,以保证完成的有效性。
亮点
PANC的亮点主要包括:
(1)利用实体和模糊聚类算法之间的相关性来获得每个原型每个实体的成员关系,以便将实体划分为相应的原型空间,并使用原型信息构建我们的过滤器,以生成更合理的候选(r,t)对。
(2)引入局部图邻居信息来进一步约束给定的头部实体,并通过邻居聚合过滤和重新设计Grader,以增强实体嵌入。
概念及模型
Prototype segmentator
我们选择原型作为指导,原型中包含的语义信息比类型更有边界。考虑到KG中的每个实体可以有一个或多个原型,我们设计了基于模糊C-均值聚类算法的原型分割器。为了实现这个模块,我们首先将原型的数量计算为N,并将每个原型视为一个聚类中心。对于KG中的所有实体,原型分割器的目标函数定义如下:
其中m是权重指数,e和p分别表示实体的语义向量和原型的语义向量,uij表示pj的ei的隶属度。我们引入K-Means++算法来初始化原型嵌入,以确保最优解。在生成隶属度矩阵U、p的迭代过程中,原型集合及其对应实体的隶属度也将通过以下等式更新:
受Reta的启发,我们也选择张量对原型三元组(hp,r,tp)进行建模,以涵盖所有符合条件的原型组合。我们将所有的原型三元组表示为一个张量PRP,其维度是|P|×|R|×|P|,其中R和P是KG中的关系集和原型集。对于给定的头部实体h,通过原型分割器可以得到其原型向量hp→和实体-原型矩阵U。考虑到原型的粗糙性,为了避免引入大量的噪声信息,我们设置了一个阈值Q,它表示每个实体的前Q个原型。H的最终候选(r,t)对集合C可以通过张量积计算如下:
其中 C 是维度为 |R| 的张量 × |E|。最后,我们可以得到一个局部组合图,它由给定的头实体 h 及其候选日期 (r, t) 对集合 C 组成。
Neighbor grader
该模块用于通过匹配分数对过滤器提供的候选集中的 (r, t) 对进行排名。我们确定将原型视为过滤器的约束意味着我们可以获得更多可能的 (r,t) 对,以便我们可以在未来发现更多知识。然而,这也意味着我们的过滤器会给候选集带来更多的噪声,甚至可能会打破 (r, t) 对和给定实体之间的合理性假设。在增加候选集的容量的同时,确保高质量的评估是一个巨大的挑战。为了应对这一挑战,我们将邻居聚合引入Grader。
图1 邻居聚合分级器架构
图1显示了我们提出的邻居聚合分级器的架构。邻居聚合分级器的输入是由候选 (r, t) 对和给定头部实体 h 组成的局部图。此外,图 3 中的示例仅在左侧局部图中的某些三元组中得到证明。它将被发送到两个不同的子模块,分别在实体级空间和原型级空间中获得两个不同的特征嵌入。上层子模块是邻居聚合器,主要增强实体级别的实体嵌入。邻居聚合器的机制如图4所示。首先,我们需要通过d维嵌入层emb(.)将头部实体、关系和尾部实体映射到d维向量:
这里,eh、r 和 et 分别表示头部实体、关系和尾部实体,而 vh、vr 和 vt 分别表示它们对应的嵌入表示。然后,我们假设头部实体 e 有 k 个一对一hop 邻居实体,它们之间的边表示 k 个重新编译。我们可以为 e 制定邻居集 N 的定义如下:
我们定义函数 F 以增强头部实体 e 与其邻居集的嵌入表示:
其中 σ 表示一种激活函数。我们在此通常设置 σ =tanh,可以达到良好的性能。|Ne|是元素的数量,表示关系向量和尾部实体向量的组合操作。我们应用前馈网络对邻居信息进行编码:
其中⊕表示向量连接,W∈Rd×2d, b∈Rd。较低的子模块是我们在上一节中提出的原型分割器。它用于获取每个实体的原型以生成原型三元组。我们假设头部实体有 m 个原型,而尾部实体在图 3 中有 n 个原型。因此,有 m×n 个原型三元组作为特征提取器的输入。
我们提出的特征提取方法本质上是一种卷积神经网络。我们将三元组中的三个d维矢量串联成矩阵∈R3×d,并将其馈入具有L核的二维卷积层。我们设置核的大小来学习三元组中的隐藏特征,因此卷积后形成的所有特征图的大小为d2。我们将L特征图展平为一个三元组向量∈r1×L(d-2),该向量既适用于事实三元组,也适用于原型三元组,以揭示三个向量之间的联系。此外,每个事实三元组将有m×n个对应的原型三元组,最终通过特征抽取器生成m,n个原型三元组。为了保证事实三元组的真实性,原型三元组之间的关联度必须很高,这就要求每个维度的最小值不能太低。因此,我们使用最小运算,它取所有原型三重向量中每个维度的最小值。特征抽取器的输出分为实体级向量和原型级向量两部分。考虑到我们通过计算匹配分数来评估事实三元组的合理性,然后将两个向量连接成一个大小为2l(D2)的向量,并选择全连通层来获得最终的预测分数。对于正样本(h,r+,t+)和负样本(h,r-,t-),我们在前人工作的基础上,选择Softplus函数作为邻居聚集分类器的损失函数:
其中 θ+ 表示正样本,θ- 表示负样本。
实验
我们在两个流行的 KG 数据集 JF17k 和 FB15k 上评估我们的模型和基线。它们都源自流行的 KG Free-base (Bollacker et al., 2008)。对于每个实体,我们随机分配 80% 的三元组,以它为训练集,其余 20% 作为测试集。两个数据集的统计如表 1 所示,其中 #Entity、#Relation、#Prototype 和 #Fact 分别表示实体、关系、原型和事实三元组的数量。为了评估我们提出的 PANC 和实例完成任务的基线的性能,我们采用 Recall@N、平均平均精度 (MAP) 和归一化折扣累积增益 (NDCG) 作为比较的指标。Recall 是正确识别的所有正样本的比例,它可以衡量分类器识别正样本的能力。MAP是所有类中AP的平均值,其中AP被视为一个类的精度/召回曲线包围的区域。NDCG 是 DCG 的归一化,它可以衡量推荐的相关性及其位置的影响。在我们的实验中,N 设置为 5 和 10。这些指标的得分越高,模型的性能越好。
表1 实验数据集
表 2 显示 PANC 在两个数据集上的实例完成任务的评估结果。从表 2 的性能中,我们可以得出结论:
(1)在这两个数据集上,为实体补全而设计的 RETA和我们的模型都优于传统的基于距离和语义的 KG 嵌入模型,表明过滤器和分级器框架可以更准确地完成任务。此外,我们可以观察到 Analogy 可以在传统 KG 完成模型中对这两个数据集保持高度稳定的影响,这在一定程度上符合我们使用原型的动机。我们的模型和类比都使用实体的低级特征来完成任务。不同之处在于我们以原型的形式显式地向我们的模型添加信息,而它隐含地利用了这种潜在信息。这一结果也证明了该策略在辅助信息的帮助下的有效性。
(2)我们的模型显示出比所有基线显著的性能改进。与最佳基线 RETA和在Rec@10、Rec@5、MAP、NDCG 方面相比,我们的模型取得的性能提升分别为 FB15k 和 JF17k 上的 19.56%、12.88%、9.1%、12.86% 和 22.91%、20.17%、11.8%、13.4%。这些结果表明,引入原型和邻居聚合的新策略更有效和更稳健地实现了宽松的过滤器和紧密的分级器。
(3)尽管 TypeDM 和 TypeComplEx可以使用类型信息对实体和关系进行建模,并在传统的 KG 嵌入模型中更显著地执行,但由于缺少邻居信息,它可能不适用于该任务。显然,我们的模型比 TypeDM 和 TypeComplEx表现更好,受益于融合邻居信息和对邻居聚合器带来的三元组的进一步约束。
表2 实验结果
总结
本文提出了一个实体补全任务的PANC模型,该模型由两个模块组成:原型分割器和邻居评分器。原型分割器首先根据原型对所有实体进行聚类,并通过原型为给定的头部实体生成比类型更多的候选关系对集合;邻居分级算法依靠邻居聚合来增强实体嵌入,约束头部实体和候选实体对的组合,最后基于三元组的似然程度对这些候选关系对进行评估。在两个真实数据集上的实验表明了该模型的优越性,消融实验验证了邻域聚集器的有效性。在未来的工作中,将考虑更复杂的嵌入技术。
OpenKG
OpenKG(中文开放知识图谱)旨在推动以中文为核心的知识图谱数据的开放、互联及众包,并促进知识图谱算法、工具及平台的开源开放。
点击阅读原文,进入 OpenKG 网站。