【数据结构与算法】| 排序
目录
- 一、插入排序
-
- 1.直接插入排序
- 2.希尔排序(直接插入排序优化版)
- 二、选择排序
-
- 1.直接选择排序
- 2.堆排序
- 三、交换排序
-
- 1.冒泡排序
-
- 冒泡排序小结
- 2.快排
-
- 递归快排
- 快排优化
- 非递归快排
- 快排小结
- 四、归并排序
-
- 1.递归实现归并排序
- 2.非递归实现归并排序
- 3.归并排序小结
- 五、非比较排序
- 六、排序总结
一、插入排序
1.直接插入排序
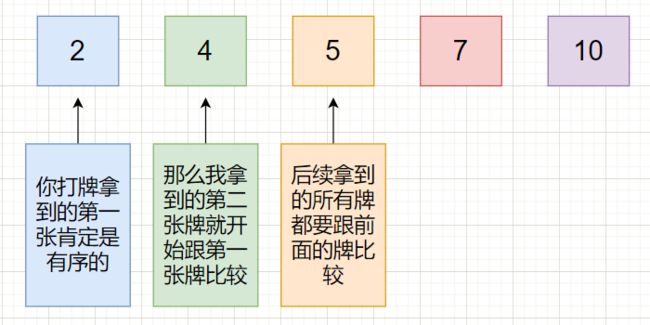
大家都应该打过扑克牌吧,插入排序就类似你扑克牌的排序。
public static void insertSort(int[] array){
for(int i=1;i<array.length;i++) {
int tmp = array[i];
int j = i-1;
for (; j >= 0; j--) {
if(array[j] > tmp) {
array[j+1] = array[j];
}
else {
break;
}
}
array[j+1] = tmp;
}
}
根据提供的代码可以自行参考上图来观察每个数字是怎么走的。
时间复杂度:o(n^2)【无序的情况】,o(n)【有序的情况】
空间复杂度:o(1)
稳定性:稳定
2.希尔排序(直接插入排序优化版)
希尔排序其实本质就是插入排序,不过希尔排序是分组的。
假如你的插入排序是排序10000个数据,在时间复杂度中 n = 10000,那么插入排序就要进行10000*10000次排序。
而希尔排序把10000个数据分成100组,每组有100个数据。那么每个组排序的次数就是100*100次,100个组总共就是100*100*100。
很明显希尔排序就把工作量降低了不少。
希尔排序的过程是这样的。
private static void shell(int[] array,int gap) {
for (int i = gap; i < array.length ; i++) {
int j = i - gap;
int tmp = array[i];
for (; j >= 0 ; j-=gap) {
if(tmp < array[j]) {
array[j+gap] = array[j];
}
else {
break;
}
}
array[j+gap] = tmp;
}
}
// 希尔排序
public static void shellSort(int[] array){
// write code here
int gap = 5;
while(gap != 1) {
shell(array,gap);
gap /= 2;
}
shell(array,1);
}
希尔排序是对插入排序的一种优化。
每一次的分组都是让数据趋于有序,从而使得排序的次数降低,因此时间复杂度也比直接插入排序快了一点。
空间复杂度:o(1)
稳定性:不稳定
二、选择排序
1.直接选择排序
基本思想:就是军队训练当中的按照身高选人,从一群人中先选出一个人,然后一一比较身高低矮,比这个高或者矮的,那么就以这个新的身高为基准,确保这个为最低或者最高的。然后第二个为基准,然后也是一一比较。
具体代码:
public static void selectSort(int[] array){
// write code here
for (int i = 0; i < array.length; i++) {
int minIndex = i;
for (int j = i+1; j < array.length; j++) {
if(array[j] < array[minIndex]) {
minIndex = j;
}
}
swap(array,i,minIndex);
}
}
第二种思路:就是在数组中每次都找到最大和最小的数据,分别放到数组的两边,然后缩小区间继续寻找最大和最小数据,直到区间剩下一个或者刚好两边都是最大和最小的。
public static void selectSort2(int[] array){
// write code here
int left = 0;
int right = array.length - 1;
while(left < right) {
int maxIndex = left;
int minIndex = left;
for (int j = left+1; j <= right; j++) {
if(array[j] < array[minIndex]) {
minIndex = j;
}
if(array[j] > array[maxIndex]) {
maxIndex = j;
}
}
swap(array,left,minIndex);
if(left == maxIndex) {
maxIndex = minIndex;
}
swap(array,right,maxIndex);
left++;
right--;
}
}
时间复杂度:o(n^2)
空间复杂度:o(1)
稳定性:不稳定
2.堆排序
堆排序如果是升序排序的话,那么就创建一个大根堆,然后每次把对顶元素都放到最后即可。
具体代码:
public static void heapSort(int[] array){
// write code here
createBigHeap(array);
int end = array.length - 1;
while(end >= 0) {
swap(array,0,end);
shiftDown(array,0,end);
end--;
}
}
private static void createBigHeap(int[] array) {
for (int parent = (array.length-1-1)/2; parent >= 0 ; parent--) {
shiftDown(array,parent,array.length);
}
}
private static void shiftDown(int[] array,int parent,int len) {
int child = 2*parent+1;
while(child < len) {
if(child+1 < len && array[child] < array[child+1]) {
child++;
}
if(array[child] > array[parent]) {
swap(array,child,parent);
parent = child;
child = 2*parent + 1;
}
else {
break;
}
}
}
时间复杂度:o(n^2)
空间复杂度:o(1)
稳定性:不稳定
三、交换排序
1.冒泡排序
冒泡排序其实就是进行n-1轮排序,每一次排序都让最大或者最小的都在最后面。
public static void bubbleSort(int[] array){
// write code here
for (int i = 0; i < array.length-1; i++) {
boolean flag = false;
for (int j = 0; j < array.length-1; j++) {
if(array[j] > array[j+1]) {
swap(array,j,j+1);
flag = true;
}
}
if(!flag) {
break;
}
}
}
如果有序则无需再排序,上面代码进行了优化。
冒泡排序小结
时间复杂度:O(n^2)
空间复杂度:O(1)
稳定性:稳定
2.快排
递归快排
快排类似二叉树的递归,也是找一个基准值,每次排序都把比基准值大的放基准值的右边,比基准值小的都放基准值的左边,直到树的节点成为了叶子节点。
1、Hoare法
public static void quickHoare(int[] array,int left,int right) {
if(left >= right) {
return;
}
int pivot = partitionHoare(array,left,right);
quickHoare(array,left,pivot-1);
quickHoare(array,pivot+1,right);
}
private static int partitionHoare(int[] array, int left, int right) {
int i = left;
int key = array[left];
//left 不用等于 right, 等于right的时候就直接交换
while(left < right) {
//这是一个单独的循环,必须还要再判断left是否小于right
//必须取等号,否则会死循环
while(left < right && array[right] >= key) {
right--;
}
while(left < right && array[left] <= key) {
left ++;
}
swap(array,left,right);
}
swap(array,i,left);
return left;
}
public static void quickSortHoare(int[] array){
// write code here
quickHoare(array,0,array.length-1);
}
2.挖坑法
private static int partitionHole(int[] array, int left, int right) {
int key = array[left];
while(left < right) {
while(left < right && array[right] >= key) {
right--;
}
swap(array,left,right);
while(left < right && array[left] <= key) {
left ++;
}
swap(array,left,right);
}
array[left] = key;
return left;
}
public static void quickHole(int[] array,int left,int right) {
if(left >= right) {
return;
}
int pivot = partitionHole(array,left,right);
quickHole(array,left,pivot-1);
quickHole(array,pivot+1,right);
}
public static void quickSortDigHole(int[] array) {
quickHole(array,0,array.length-1);
}
3.前后指针法
public static void quickPointer(int[] array,int left,int right) {
if(left >= right) {
return;
}
int pivot = partitionPointer(array,left,right);
quickPointer(array,left,pivot-1);
quickPointer(array,pivot+1,right);
}
private static int partitionPointer(int[] array, int left, int right) {
int prev = left;
int cur = left+1;
while(cur <= right){
if(array[cur] <= array[left] && array[++prev] != array[cur]) {
swap(array,cur,prev);
}
cur ++;
}
swap(array,left,prev);
return prev;
}
public static void quickSortPointer(int[] array) {
quickPointer(array,0,array.length-1);
}
快排优化
三数取中法
递归对堆栈有要求,所以三数取中法是为了让取基准值的时候,让基准值处在一个比较中间的位置,使得递归的次数减少。
private static int findMidNumIndex(int[] array,int left,int right) {
int mid = (left+right) / 2;
if(array[left] > array[right]) {
if(array[right] > array[mid]) {
return right;
}else if(array[mid] > array[left]) {
return mid;
}else {
return left;
}
}else {
if(array[left] > array[mid]) {
return left;
}else if(array[mid] > array[right]) {
return right;
}else {
return mid;
}
}
}
求得一个比较中间的数之后,然后跟数组的第一个元素对换,让这个中间值成为基准值,就会使得后面的递归都趋于二分,会有效的减少递归的次数。
public static void quickHoare(int[] array,int left,int right) {
if(left >= right) {
return;
}
int ret = findMidNumIndex(array,left,right);
swap(array,left,ret);
int pivot = partitionHoare(array,left,right);
quickHoare(array,left,pivot-1);
quickHoare(array,pivot+1,right);
}
还有一种优化就是,在递归了很多次后,数据都会趋于有序化,那么此时使用直接插入排序会更优化一些。
public static void insertSort(int[] array,int left,int right){
// write code here
//这里取等号,是因为接口处减了1
for(int i=left+1; i <= right;i++) {
int tmp = array[i];
int j = i-1;
for (; j >= left; j--) {
if(array[j] > tmp) {
array[j+1] = array[j];
}
else {
break;
}
}
array[j+1] = tmp;
}
}
非递归快排
模拟实现非递归就要用到栈。思想也是一样,把每一段都分为左右两边。先找基准值,栈中的数据存储的就是数组的下标,然后弹出作为新的左右下标,直到栈为空,则排序完成。
快排小结
时间复杂度:O(n*logn)
空间复杂度:O(1)
稳定性:不稳定
public static void quickSortNotCircle(int[] array) {
Stack<Integer> s = new Stack<>();
int left = 0;
int right = array.length-1;
int index = findMidNumIndex(array,left,right);
swap(array,left,index);
int pivot = partitionPointer(array,left,right);
if(left+1 < pivot) {
s.push(left);
s.push(pivot-1);
}
if(right-1 > pivot) {
s.push(pivot+1);
s.push(right);
}
while(!s.isEmpty()) {
right = s.pop();
left = s.pop();
pivot = partitionPointer(array,left,right);
if(left+1 < pivot) {
s.push(left);
s.push(pivot-1);
}
if(right-1 > pivot) {
s.push(pivot+1);
s.push(right);
}
}
}
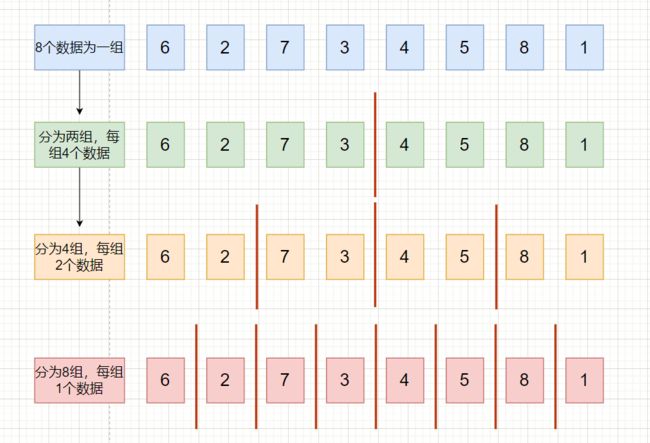
四、归并排序
归并排序的思想就是把数据都分成一个一个的,因为一个数据必然是有序的,然后再把一个一个的数据比较进行合并。
1.递归实现归并排序
分组代码如下:
private static void mergeFunc(int[] array,int left,int right) {
if(left >= right) {
return ;
}
int mid = (left + right) / 2;
//1.分解左边
mergeFunc(array,left,mid);
//2.分解右边
mergeFunc(array,mid+1,right);
}
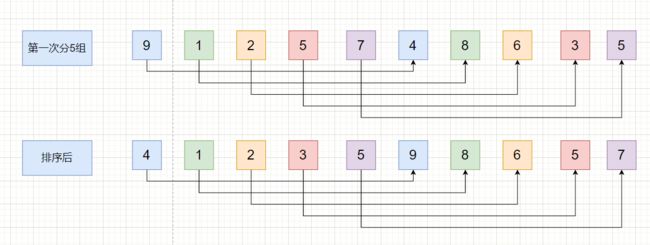
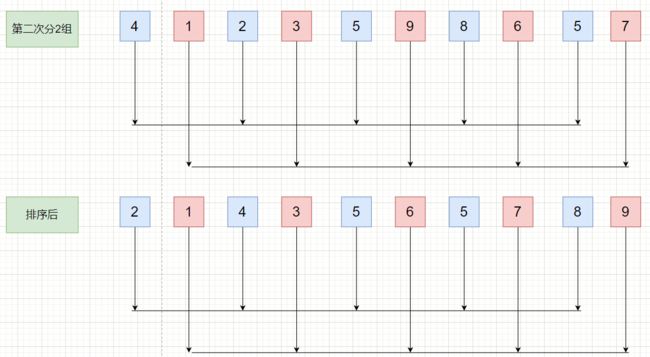
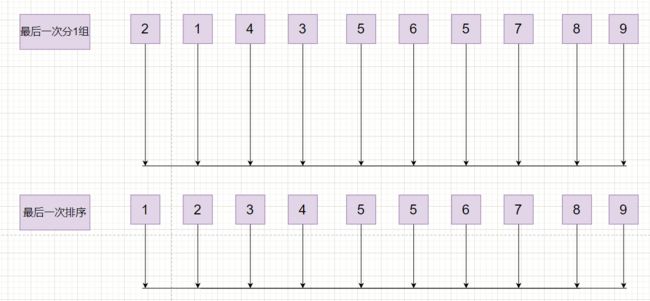
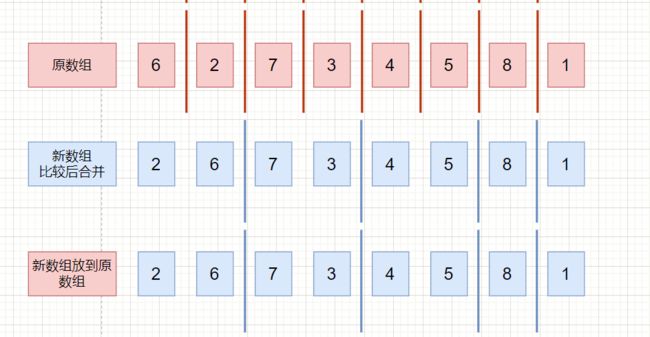
合并示意图:
从单个有序的元素开始一直合并,每次合并都创建新数组,合并完成后放回原数组,知道整个数组都排序完成。
private static void merge(int[] array,int start,int mid,int end) {
//创建新的数组接收
int[] tmp = new int[end-start+1];
//新数组下标
int k = 0;
int s1 = start;
int e1 = mid;
int s2 = mid+1;
int e2 = end;
while(s1 <= e1 && s2 <= e2) {
if(array[s1] <= array[s2]) {
tmp[k] = array[s1];
k++;
s1++;
}
else {
tmp[k] = array[s2];
k++;
s2++;
}
}
//代码来到这里,要么s1 > e1,要么 s2 > e2
while(s1 <= e1) {
tmp[k++] = array[s1++];
}
while(s2 <= e2) {
tmp[k++] = array[s2++];
}
for (int i = 0; i < k; i++) {
array[i+start] = tmp[i];
}
}
2.非递归实现归并排序
非递归的思想就是把一整个数组也是分为一个一个的数据来比较,使其趋于有序化,然后扩大范围再次使其有序化,直到整个数组都有序。
具体的画图跟上面递归相似,我不再画了,直接上代码。
public static void mergeSortNotCircle(int[] array){
// write code here
int gap = 1;
while(gap < array.length) {
for (int i = 0; i < array.length; i += gap*2) {
int s1 = i;
int e1 = i+gap-1;
if(e1 >= array.length) {
e1 = array.length-1;
}
int s2 = e1+1;
if(s2 >= array.length) {
s2 = array.length-1;
}
int e2 = s2+gap-1;
if(e2 >= array.length) {
e2 = array.length-1;
}
merge(array,s1,e1,e2);
}
gap *= 2;
}
}
3.归并排序小结
时间复杂度:O(n*logn)
空间复杂度:O(n)
稳定性:稳定
五、非比较排序
计数排序,这个排序很有趣,不需要比较,在我看来就是利用数组下标的有序性来比较。
难点是在于怎么确定新数组的大小。
public static void countSort(int[] array){
// write code here
int maxval = array[0];
int minval = array[0];
for (int i = 0; i < array.length; i++) {
if(array[i] > maxval) {
maxval = array[i];
}
if(array[i] < minval) {
minval = array[i];
}
}
int len = maxval - minval + 1;
int[] count = new int[len];
for (int i = 0; i < count.length; i++) {
count[array[i] - minval] ++;
}
int index = 0;
for (int i = 0; i < count.length; i++) {
while(count[i] != 0) {
array[index] = i + minval;
index ++;
count[i]--;
}
}
}
六、排序总结
| 排序方法 | 最好 | 平均 | 最坏 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 插入排序 | O(n) | O(n^2) | O(n^2) | O(1) | 稳定 |
| 选择排序 | O(n^2) | O(n^2) | O(n^2) | O(1) | 不稳定 |
| 希尔排序 | O(n) | O(n^1.3) | O(n^2) | O(1) | 不稳定 |
| 堆排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(1) | 不稳定 |
| 快速排序 | O(n * log(n)) | O(n * log(n)) | O(n^2) | O(log(n)) ~ O(n) | 不稳定 |
| 归并排序 | O(n * log(n)) | O(n * log(n)) | O(n * log(n)) | O(n) | 稳定 |