PCA主成分分析 | 机器学习

1、概述(Principal componet analysis,PCA)

是一种无监督学习方法，是为了降低特征的维度。将原始高维数据转化为低维度的数据，高维数据指的是数据的特征维度较多，找到一个坐标系，使得这些数据特征映射到一个二维或三维的坐标系中，尽可能地保留原始数据的主要信息（方差信息），信息损失是最小的。
举个例子： 在实际工作中，可能会遇到特征维数过多，且部分特征具有一定相关性。如：在一个学生成绩数据集中，一个特征是学习时长，另一个特征是成绩，一般来讲，学习时间越长，越容易取得好成绩，即时长与成绩呈正相关。因此没必要用两个维度（时长和成绩）表达这一特征。我们可以找出另一个维度，表现这两个特征，且不会带来过多信息损失。
信息保留最多（从图像上看就是越分散，方差越大。如果点都比较重合，失去了意义）


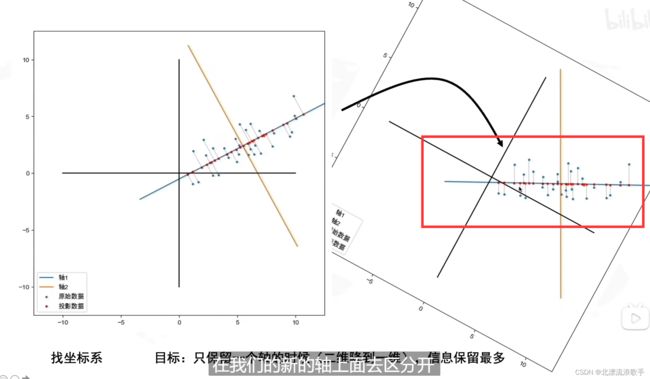
怎么样最好：
找到数据分布最分散的方向（方差最大），作为主成分（坐标轴）
利用正交变换把线性相关变量表示的观测数据转换为几个由线性无关变量表示的数据，线性无关的变量成为主成分。主成分的个数通常小于原始变量的个数，属于降维方法。
根据分解协方差矩阵的策略，分为两种PCA方法，第一种是基于特征值分解协方差矩阵实现PCA算法，第二种是**基于奇异值分解法(SVD)**分解协方差矩阵实现PCA算法。
PC：找到的每个新特征向量，降低特征个数，降维找出数据中最主要的，用最主要的代替原始数据。非监督的降维方法
信息衡量指标： 样本方差，方差越大，特征所带信息量越多。

2、算法流程

输入：n维样本集D=(x(1),x(2),…,x(m))，要降维到的维数n’.
输出：降维后的样本集D′
1 .数据标准化
对所有样本进行中心化（把坐标原点（0，0）放在数据中心，数据中心通过计算均值，样本-均值）；第二是找坐标系（找到方差最大的方向）；

2 计算样本协方差矩阵XXT
将标准化后的数据组成一个n×d的矩阵X，其中n表示样本数量，d表示特征数量。计算协方差矩阵C=XTX/n-1。因为样本协方差矩阵XXT包含了数据的方差和协方差信息。

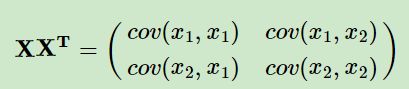
3.计算特征值和特征向量：
对协方差矩阵进行特征值分解，得到特征值λ1,λ2,…,λd和对应的特征向量v1,v2,…,vd。特征向量是单位向量，满足Cvi=λivi。对协方差矩阵进行特征值分解，将特征值从大到小排列。
那么为什么计算呢，要通过计算协方差矩阵的特征值和特征向量，我们可以找到原始数据中最具有代表性的主成分（也就是方差最大的方向），从而实现降维。因为在PCA中，特征值是协方差矩阵的特殊值，代表着数据在某个方向上的方差大小。具体来说，对于一个d维数据集，其协方差矩阵C的每个特征值λi表示数据在第i个主成分方向上的方差大小。λi越大，说明数据在第i个主成分方向上的方差越大，也就是说，这个方向上的信息量越多，越能够代表原始数据的特征。因此，在PCA中，我们通常选择前k个最大的特征值对应的特征向量作为新的坐标系，并将原始数据投影到这个新的坐标系上，从而实现降维。
在PCA中，特征值是协方差矩阵的特殊值，代表着数据在某个方向上的方差大小。具体来说，对于一个d维数据集，其协方差矩阵C的每个特征值λi表示数据在第i个主成分方向上的方差大小。λi越大，说明数据在第i个主成分方向上的方差越大，也就是说，这个方向上的信息量越多，越能够代表原始数据的特征。因此，在PCA中，我们通常选择前k个最大的特征值对应的特征向量作为新的坐标系，并将原始数据投影到这个新的坐标系上，从而实现降维。
接下来用数据例子说明下
假设我们有一个2维数据集，包含5个样本点：

X = [[2, 3], [3, 4], [4, 5], [5, 6], [6, 7]]

我们希望对这个数据集进行降维，将其从2维降到1维。首先，我们需要计算协方差矩阵C：

C = np.cov(X.T)

计算得到的协方差矩阵C为：

array([[ 0.7,  0.7],
       [ 0.7,  0.7]])

接下来，我们需要计算C的特征值和特征向量：

eig_vals, eig_vecs = np.linalg.eig(C)

计算得到的特征值和特征向量为：

eig_vals = [1.4, 0]
eig_vecs = [[ 0.70710678, -0.70710678],
            [ 0.70710678,  0.70710678]]

由于我们希望将数据从2维降到1维，因此我们只需要选择最大的特征值对应的特征向量作为新的坐标系。在这个例子中，最大的特征值为1.4，对应的特征向量为[0.70710678, -0.70710678]。因此，我们可以将原始数据投影到这个新的坐标系上，得到降维后的数据：

new_X = np.dot(X, eig_vecs[:, 0])

计算得到的降维后的数据为：

array([ 0.        ,  0.70710678,  1.41421356,  2.12132034,  2.82842712])

可以看出，原始的2维数据集被成功地降到了1维，并且保留了原始数据的大部分信息。
4.选择主成分：
将特征值从大到小排序，选择前k个特征值对应的特征向量作为主成分，其中k是降维后的维度。
5.映射数据：
将原始数据X映射到主成分上，得到新的降维后的数据Y=XV，其中V=[v1,v2,…,vk]是由前k个特征向量组成的矩阵。

矩阵分解：
找出n个新特征向量，让data被压缩到少数特征上并且总信息量不损失太多的技术。

3、降维目的

只保留一个轴的时候，（二维降低到1维度，相当于两个线性相关的变量，一个是可以用另一个表征的，用一个坐标轴来表示，另一个坐标轴就是0，将二维信息降低到1维存储），信息保留最多。

将高纬度数据保留下一些重要特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的
去噪：使主要的特征避免被干扰，使其与其他维度相关性尽可能减弱，进而恢复应有的能量。
去冗余 所有样方差接近于0，不重要

由图可知，可以用数据点在 Z 轴上的投影表达时长与成绩两个维度的数据。一个平面上的数据就被映射到了一条线当中，即二维特征向一维特征的转换。

4、为什么要用协方差矩阵来做呢

协方差矩阵能同时表现不同维度间的相关性及各个维度上的方差，矩阵主对角线上原色是各个特征的方差，其他元素是两两特征见的协方差（即相关性）去噪-让协方差据阵容非对角线元素基本为0，矩阵对角化。去冗余-对角化后的协方差矩阵，对角线上较小的新方差就是那些该去掉的维度，所以只取那些含有较大能量（特征值），其余舍掉。

[[ 1.11111111, 0.87904968, 1.06804138, 0.4138031 ],
[ 0.87904968, 1.11111111, 1.28488947, 0.47746479],
[ 1.06804138, 1.28488947, 1.55555556, 0.49690399],
[ 0.4138031 , 0.47746479, 0.49690399, 1.11111111]]，
那么在协方差矩阵中相邻两个元素代表什么含义呢
在协方差矩阵中，第i行第j列的元素表示第i个特征和第j个特征之间的协方差。因此，这个矩阵中相邻两个元素代表了两个不同特征之间的协方差。例如，第1行第2列和第2行第1列的元素都是0.87904968，表示第1个特征和第2个特征之间的协方差为0.87904968。由于协方差矩阵是对称矩阵，因此这两个元素的值是相等的。同理，第1行第3列和第3行第1列的元素、第2行第3列和第3行第2列的元素、以及第2行第4列和第4行第2列的元素、第3行第4列和第4行第3列的元素，也都分别代表了两个不同特征之间的协方差。

PCA优缺点
优点
1 仅以方差衡量信息量，不受数据集以外的因素影响
2各个主成分之间正交，可消除原始数据成分间相互影响的因素
3 计算简单
缺点
1 解释性差
2 方差小的非主成分也可能含有对样本差异的重要信息，降维可能对后续数据有影响

PCA适用场景
非监督式，适用于不带有标签的数据集，对于有标签的可用LDA。
数据量多和维度多，处理

5、代码

原始数据矩阵的行数代表样本数量，列数代表每个样本的特征数量。在这个例子中，原始数据矩阵的维度为5x3，即有5个样本，每个样本有3个特征。
以一个具体的例子来解释，假设我们要对一组人群进行身高、体重和年龄的测量，我们可以将每个人看作一个样本，将他们的身高、体重和年龄看作样本的3个特征。如果我们测量了100个人，那么我们就可以得到一个100x3的数据矩阵，其中有100个样本，每个样本有3个特征。同样地，如果我们测量了1000个人，那么我们就可以得到一个1000x3的数据矩阵，其中有1000个样本，每个样本有3个特征。

参考链接：

https://blog.csdn.net/babywong/article/details/50085239
https://betterbench.blog.csdn.net/article/details/127065371
https://zhuanlan.zhihu.com/p/76057643
https://www.xiaohongshu.com/discovery/item/62937d4b0000000021035695