无线感知论文阅读笔记 | TRS 2023, DeepEgo: Deep Instantaneous Ego-Motion Estimation Using Automotive Radar

原文链接：https://mp.weixin.qq.com/s?__biz=Mzg4MjgxMjgyMg==&mid=2247486296&idx=1&sn=593f29ee45f66782e90b247b635696d1&chksm=cf51b9a1f82630b7c6ac427f98bb03c18015b6b1865fec22a8c2465768c6fdf463a5c81ef305#rd

TRS 2023 | DeepEgo: Deep Instantaneous Ego-Motion Estimation Using Automotive Radar

无线感知论文阅读笔记 | TRS 2023, DeepEgo: Deep Instantaneous Ego-Motion Estimation Using Automotive Radar

Abstract

• 目标

  • Study ego-motion estimation with mm-wave radar

• Propose DeepEgo for robust and accurate estimation

  • 使用神经网络从点云中提取特征
  • 应用加权最小二乘进行运动估计
  • 新的损失函数：提出多普勒损失定位内点

• Experiments

  • Test on real-world automotive radar dataset
  • Show improvements in accuracy, stability and runtime

1 Introduction

• 背景

  • 高级驾驶系统(ADS)需要实时的自我运动估计

  • 传统方法（如IMU、车轮编码器和GPS）存在诸多问题 $\Rightarrow$ 采用其他传感器技术（如摄像头、激光雷达、合成孔径声纳、扫描雷达或汽车雷达）进行自我运动估计

  • 汽车雷达具有一定优势

    ✅ 如适应各种天气和照明条件、对线视遮挡的敏感性较低、轻量化、低成本和紧凑

    ❌ 尽管汽车雷达具有潜在优势，但仍存在挑战，如较少的几何特征、假正例、漏检、雷达截面波动、多路径反射和互干扰等。

• 本文：DeepEgo

  • 基于神经网络的端到端自我运动估计解决方案，避免了具有挑战性的数据关联任务

  • 提出了一种混合方法：

    神经网络学习如何加权雷达点云中的每个点

    加权最小二乘法(WLS)用于计算最终的估计结果

  • 提出了一种新颖的损失函数: 多普勒损失

    多普勒损失可以帮助网络自动定位雷达点云中的“内点”,而无需手动标注 $\Rightarrow$ important to WLS

  • 实验

    使用具有挑战性的真实汽车雷达数据集RadarScenes, 与6个baselines比较

    Improves accuracy by over 50%

• 章节安排

  • section 2: related work
  • section 3: design details of the proposed method
  • section 4: performance of the proposed method
  • section 5: ablation study
  • section 6: conclusions and future studies

2 RELATED WORKS

1. 使用汽车雷达进行自我运动估计

   • ICP and NDT are early iterative matching methods, but have limitations
   • Kellner et al. propose single-frame estimation method based on radial velocity profile
   • But Kellner method has difficulty in parameter tuning and cannot fully utilize other radar information

2. 点云深度学习

   • Image projection methods destroy point cloud structure
   • Voxel-based methods have high computational and memory costs
   • Point-based methods like PointNet can directly process high-dim sparse radar point clouds
   • This paper:

   ✅ believe point-based methods are more suitable for preserving precise geometry, processing automotive radar data

3 METHODOLOGY

A. Problem Statement

• 本文考虑多维雷达点云$P_{t,n}^{J\times M}$

  • $t$ 雷达扫描的时间戳
  • $n$ 雷达索引
  • $J$ 检测到的点的数量
  • $M$ 点云中每个点的特征数量

• 车辆运动状态：$e_c=[v_x^c,v_y^c,{\omega }^c]$

  • 2D坐标系的原点位于车辆质心处,x轴方向与车辆的距离方向运动一致,y轴方向与车辆的横向运动一致

  • $v_x^c$ 距离方向速度
  • $v_y^c$ 横向速度
  • ${\omega }^c$ 旋转速度
  • $c$ 测试车辆

• 汽车雷达

  • $n$个
  • 安装位置 $[x_n^c,y_n^c,{\theta }_n^c]$
  • 其中$x_n^c$ 到x轴距离
  • $y_n^c$ 到y轴的距离
  • ${\theta }_n^c$ 相对于车辆x轴的安装角度

雷达测量的是它自身与检测对象之间的相对运动 $\Rightarrow$ 可将车辆坐标系中的自我运动转换到雷达坐标系

• 坐标转换

  • 对于雷达坐标系,通常假设x轴方向与雷达的视线方向一致

  • 雷达$n$的2D运动状态：$e_n=[v_x^n,v_y^n,{\omega }^n]$

    ✅ $v_x^n$ 距离方向速度

    ✅ $v_y^n$ 横向速度

    ✅ ${\omega }^n$ 旋转速度

  • ${\omega }_n={\omega }_c$: 刚体上的所有点经历相同的角速度

  • 因此， 运动状态$e_c$和$e_n$之间的转换可以表示为：

[ v x n v y n ω n ] = [ cos ⁡ ( θ n c ) sin ⁡ ( θ n c ) 0 − sin ⁡ ( θ n c ) cos ⁡ ( θ n c ) 0 0 0 1 ] [ 1 0 − y n c 0 1 x n c 0 0 1 ] [ v x c v y c ω c ] 等式 1 \left[\begin{array}{c}v_x^{\mathbf{n}} \\ v_y^{\mathbf{n}} \\ \omega^{\mathbf{n}}\end{array}\right]=\left[\begin{array}{ccc}\cos \left(\theta_{\mathbf{n}}^c\right) & \sin \left(\theta_{\mathbf{n}}^c\right) & 0 \\ -\sin \left(\theta_{\mathbf{n}}^c\right) & \cos \left(\theta_{\mathbf{n}}^c\right) & 0 \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{ccc}1 & 0 & -y_n^c \\ 0 & 1 & x_n^c \\ 0 & 0 & 1\end{array}\right]\left[\begin{array}{c}v_x^{\mathbf{c}} \\ v_y^{\mathbf{c}} \\ \omega^{\mathbf{c}}\end{array}\right] 等式1 ​vxn​vyn​ωn​ ​= ​cos(θnc​)−sin(θnc​)0​sin(θnc​)cos(θnc​)0​001​ ​ ​100​010​−ync​xnc​1​ ​ ​vxc​vyc​ωc​ ​等式1

可见：如果可以估计雷达的运动状态,则可以获得车辆的自身运动

• 雷达运动状态估计 ：利用检测到的静止物体的测量径向速度和到达角信息来实现

  • 给定雷达点云$P_{t,n}^{J\times M}$
  • $M\ge 2$: 包含径向速度和到达角测量
  • 点云中第$j$个检测点$p_j$的径向速度和到达角: $p_j=[d_j^n,{\alpha }_j^n]$,单位为{m/s,弧度}
  • 假设所有$J$个检测点都来自静止物体,则雷达运动状态与径向速度测量之间的关系可以表示为: [ d 1 n d 2 n ⋮ d J n ] = − [ cos ⁡ ( α 1 n ) sin ⁡ ( α 1 n ) cos ⁡ ( α 2 n ) sin ⁡ ( α 2 n ) ⋮ ⋮ cos ⁡ ( α J n ) sin ⁡ ( α J n ) ] [ v x n v y n ] \left[\begin{array}{c}d_1^{\mathbf{n}} \\ d_2^{\mathbf{n}} \\ \vdots \\ d_J^{\mathbf{n}}\end{array}\right]=-\left[\begin{array}{cc}\cos \left(\alpha_1^n\right) & \sin \left(\alpha_1^n\right) \\ \cos \left(\alpha_2^n\right) & \sin \left(\alpha_2^n\right) \\ \vdots & \vdots \\ \cos \left(\alpha_J^n\right) & \sin \left(\alpha_J^n\right)\end{array}\right]\left[\begin{array}{c}v_x^{\mathbf{n}} \\ v_y^{\mathbf{n}}\end{array}\right] ​d1n​d2n​⋮dJn​​ ​=− ​cos(α1n​)cos(α2n​)⋮cos(αJn​)​sin(α1n​)sin(α2n​)⋮sin(αJn​)​ ​[vxn​vyn​​]
  • 所有径向速度测量的向量表示为$D$,径向速度投影矩阵的负表示为$A$,$v_x^n$和$v_y^n$的向量表示为$V$ $\Rightarrow$ $D=A\cdot V$

• 结论：

  • 1 给定至少两个独立的检测点($J\ge 2$),可以使用标准回归方法(如最小二乘法)来估计$v_x^n$和$v_y^n$:

    ✅ $$V_{est}=(A^{T}A{)}^{-1}{A}^{T}D$$

    ❌ 最小二乘法对异常值非常敏感

    ❌ radar PCD中异常值常见

  • 2 假设 $v_y^c=0$ (无横向运动)，已知 $v_x^n$和$v_y^n$的估计以及雷达位置$[x_n^c,y_n^c,{\theta }_n^c]$，根据等式1可以计算出车辆的自身运动:

    ✅ $\begin{array}{rl}{v}_x^{\mathbf{c}}& =v_x^{\mathbf{n}}\cos \left({\theta }_{\mathbf{n}}^c\right)-v_y^{\mathbf{n}}\sin \left({\theta }_{\mathbf{n}}^c\right)+{\omega }^{\mathbf{c}}{y}_{\mathbf{n}}^c\\ {\omega }^{\mathbf{c}}& =\frac{v_y^{\mathbf{n}}\cos \left({\theta }_{\mathbf{n}}^c\right)+v_x^{\mathbf{n}}\sin \left({\theta }_{\mathbf{n}}^c\right)}{x_{\mathbf{n}}^c}\end{array}$

  • 要解决的问题：如何尽可能准确地估计$v_x^n$和$v_y^n$ + 考虑雷达点云中存在的异常值。

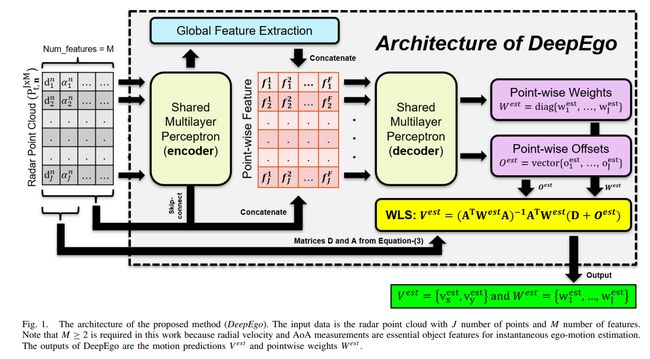
B System Architecture

• 系统架构

  • 输入: 由雷达点云组成的多维张量$P_{t,n}^{J\times M}$
  • DeepEgo:使用神经网络从雷达点云提取特征, 预测点间权重和偏移
  • 基于WLS + 网络输出 估计运动
  • 输出: 运动状态

• DeepEgo网络结构

  • 使用shared-MLP编码点云特征
  • 混合局部和全局特征以提高预测准确度
  • 分别预测点间权重和偏移

点间权重的意义：直接缩小异常值造成的大的拟合误差
点间偏移的意义：进一步减小 “远处”异常值引起的误差

C Loss function

• 损失函数

  • 包含运动损失、多普勒损失和样本权重
  • 运动损失衡量估计运动和真实运动的误差
  • 多普勒损失利用真实运动指导网络学习点的权重
  • 样本权重降低“坏”训练样本的影响

• 运动损失：

  • $Los{s}_{Motion}=\frac{1}{B}{\sum }_{b=1}^B\Vert V_{gt}^b-V_{est}^b{\Vert }^2$

  • 仅使用运动损失进行训练的一个直接后果：

    ✅ 模型倾向于在少数几个点(异常值)上过拟合,而忽略许多内点

• 多普勒损失

  • 计算预期和测量径向速度之间的差异
  • 假设差异符合均值为零的高斯分布
  • 检测点为内点的点间似然度: $W_{gt}=\frac{1}{\sigma \sqrt{2\pi }}\cdot \exp (-\frac{(D_{err}-0{)}^2}{2{\sigma }^2})$
  • 使用MSE指标计算多普勒损失: $Los{s}_{Doppler}=\frac{1}{B}{\sum }_{b=1}^B\Vert W_{gt}^b-W_{est}^b{\Vert }^2$

  ❌ 前提假设: 即所有检测到的静止物体的径向速度测量都遵循等式2

  ✅ 为了减轻“坏”训练样本的影响,本文提出了样本权重对每个训练数据进行单独加权

• 样本权重

  • 对每个训练样本进行单独加权
  • 赋予更高权重给更多内点的样本
  • 样本权重$S$是点间似然度$W_{gt}$的总和: $S=\{s_1,...s_B\}=\{{\sum }_{j=1}^J(W_{gt}^{1,j}),...,{\sum }_{j=1}^J(W_{gt}^{B,j})\}$

• 总loss

  • $Los{s}_{all}=(Los{s}_{Motion}+\mu \cdot Los{s}_{Doppler})\cdot S$

D Implementation Details

1. Shared MLP

   • 用于点云特征编码和解码
   • 包含多层全连接神经网络和批标准化
   • 使用ReLU激活函数

2. Data processing

   • 重采样到固定数量的点
   • 删除点数太少的点云
   • 归一化特征(径向速度和到达角除外)

3. Network training

   • Use mini-batch gradient descent and RMSProp
   • 20% data for validation
   • Stop when validation loss stops decreasing

4. Multiple radars

   • Each radar needs separately trained network copy

4. RESULTS AND DISCUSSIO

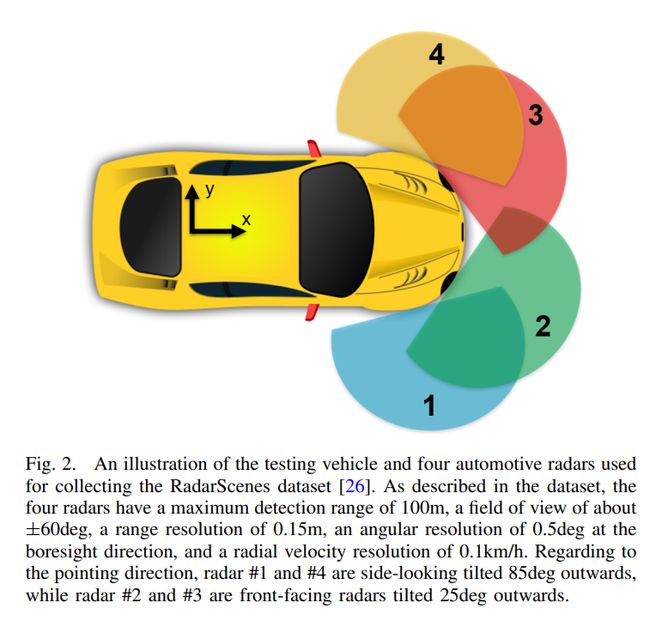
A Radar Dataset

• 雷达数据集

  • 使用RadarScenes真实世界数据集
  • 包含4个汽车雷达在各种场景下的记录
  • 选择车辆行驶距离超过500米的序列

• 数据统计

  • 选择64个数据序列
  • 总行驶距离超过79公里
  • 输入特征为4维(到达角、速度、距离、返回功率)

B. Evaluation Metrics

• 评估指标

  • APE计算估计值和真实值之间的姿态RMSE
  • 分别指示平移和旋转误差
  • RTE计算轨迹段终点距离的均方, 反映方法的长期漂移稳定性

• APE

  • 直接指示测试方法的估计准确度
  • 无法反映漂移效应,大误差可能被掩盖

• RTE

  • 将轨迹分段后计算段间终点距离
  • 分析测试方法在预定距离上的漂移稳定性

C. Selected Methods for Comparison

• Compared methods

  • Biber:第一个NDT方法
  • Kellner:基于AoA-速度轮廓的即时方法
  • Rapp:改进的NDT方法
  • Lu:基于深度学习的雷达配准
  • Heller:将NDT扩展到3D极坐标
  • Kung:用于汽车雷达的NDT流水线

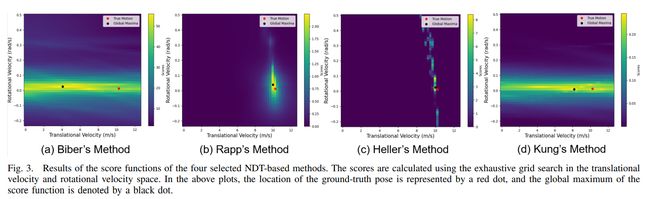
• most competitive NDT method

  • 比较4种NDT方法的分数函数
  • Rapp的方法更可能收敛到全局最优
  • 因此选择Rapp作为最具竞争力的NDT方法

D. Results of Comparison With SOTA Methods

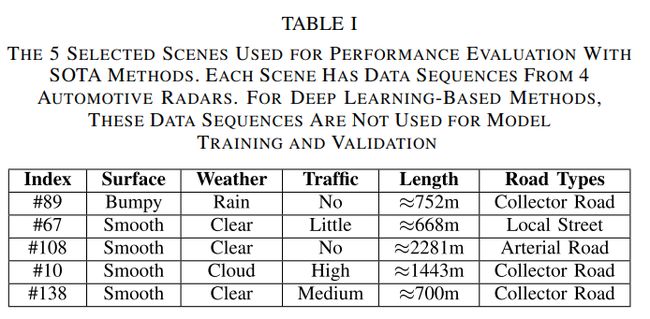
• 用于比较的五个场景

  • 覆盖了各种天气、交通和道路类型条件
    

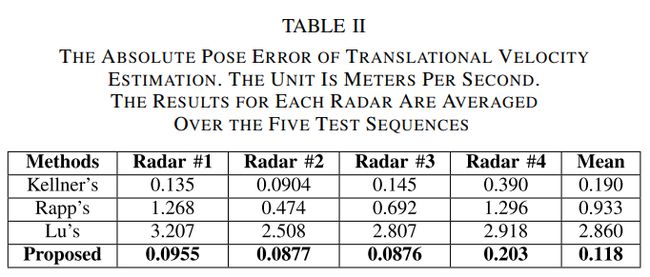
• Translation velocity estimation

  • Lu方法表现最差
  • Kellner方法最准
  • 所提方法优于Kellner 37.9%
    

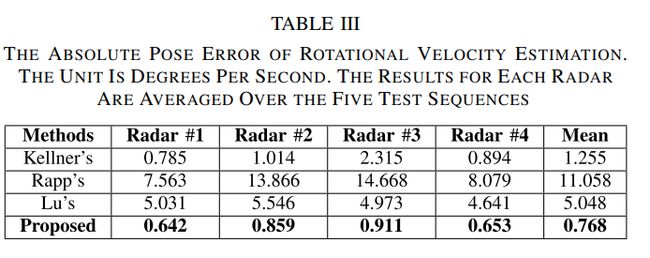
• Rotation velocity estimation

  • 侧视雷达更敏感
  • 所提方法优于最新状态 38.8%
    

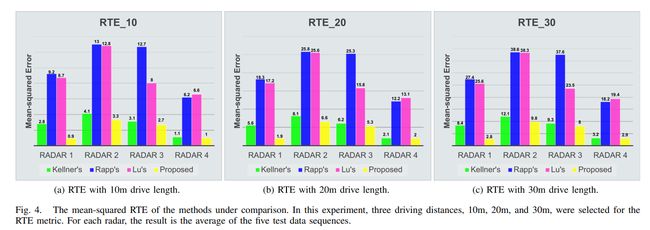
• Long-term stability

  • RTE评估不同距离
  • 所提方法RTE最低
  • Kellner方法也较好

  

• Runtime

  • Rapp方法最慢,需要优化
  • Lu方法快但网络大
  • 所提方法最快,无需迭代
    

• Visualized trajectories

  • Lu和Rapp方法较大漂移
  • Kellner方法较好
  • 所提出方法最好，特别是侧视雷达
    

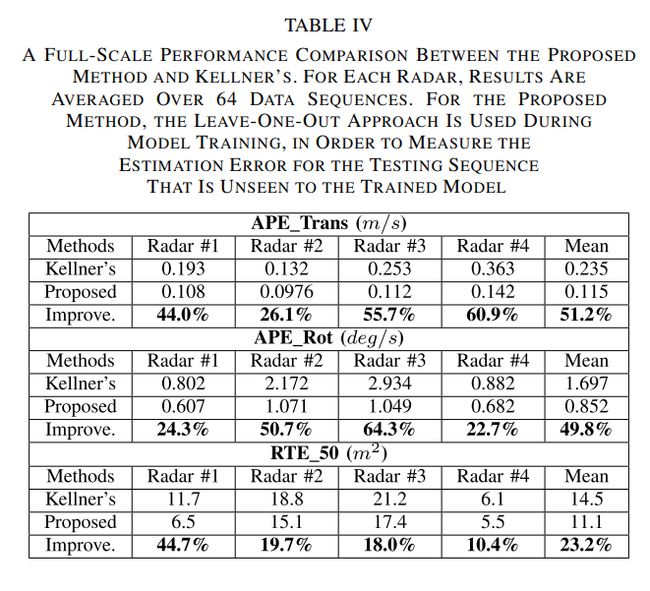
E. Further Results on All Data

• 全数据集结果

  • 使用64个序列,超过79公里
  • 与Kellner方法比较
  • 所提方法所有指标明显优于Kellner

• 误差分析

  • 绘制估计误差分布直方图
  • 直行时误差集中在旋转速度接近零区
  • 所提方法高速和快速转弯时误差较小

  ✅ 这对行车安全更重要

5. ABLATION STUDY

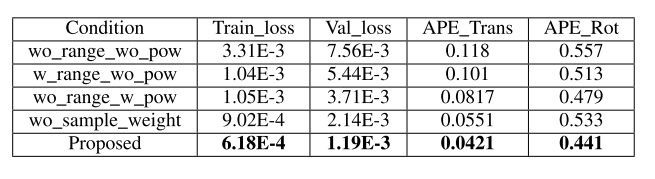
A. Ablation Study on Input Features

• 加权训练数据提高性能
• 避免模型仅依赖几个关键点

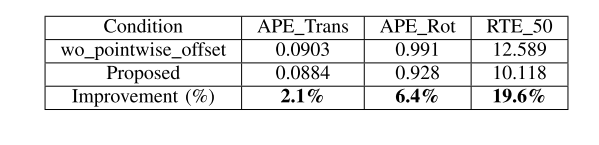
B. Effect of Pointwise Offset

• 减少离群点的影响
• 改善估计精度和长期稳定性

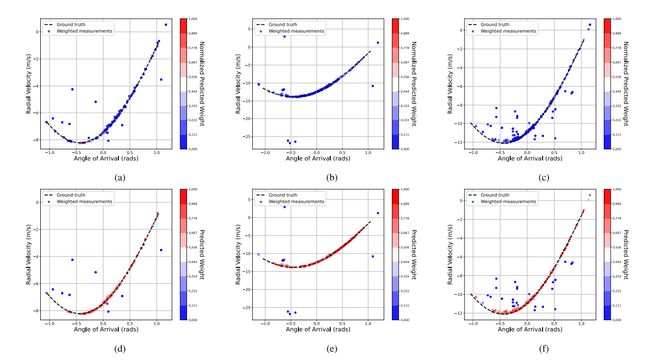
C. Effect of Doppler Loss

• 指导网络关注正确的测量
• 使用更多测量增强鲁棒性
• 权重可帮助其他应用

6 CONCLUSION

• Summary of paper

  • Propose DeepEgo for radar ego-motion estimation

    ✅ Hybrid architecture: NN feature extraction + WLS estimation

    ✅ Can directly process multi-dim point clouds, end-to-end trainable

    ✅ Provides pointwise weights associated with motion

  • Outperforms others on real dataset

• Future work

  • Currently considers single sensor
  • Could explore sensor fusion
  • Could improve robustness to different installations