Leetcode-java
目录
-
- 其他难题
-
-
-
-
- 33、搜索旋转排序数组
- 5、最长回文子串
-
-
-
- 递归
-
-
-
-
- 最大公约数
- 二叉搜索树的范围和 938
- 递归乘法 面试题08.05
- 二叉搜索树节点的最小距离 783
- 最长同值路径 687 20200722
- 数值的整数次方
-
-
-
- 动态规划
-
-
-
-
- 礼物的最大价值
- 最小路径和
- 三角形最小路径和
- 买卖一次 股票的最大利润
- 机器人路径问题
- 有障碍物的机器人路径问题
- 完全平方数
- 剪绳子
- 最长上升子序列
- 判断子序列
-
-
-
- 回溯
-
-
-
-
- 全排列 46
- 全排列 II 47
- 分割回文串
- 字符串生成
- 括号生成
- 子集78
- 复原ip地址 93
- 电话号码组合
- 组合总和
- 组合总和||
- 单词搜索
- 复原ip地址
-
-
-
- 简单
-
-
-
-
- 跳水板 面试题16.11
-
-
-
- 数组
-
-
-
-
- 区间合并
- 超过数组的一半的数
- 三数之和为0
-
-
-
- 字符串
-
-
-
-
- 两个大数字符串求和输出字符串
- 符号配对,如{}为true,{[}为false
-
-
-
- 排序
-
-
-
-
- 插入排序
- 冒泡排序
- 归并排序
- 快速排序
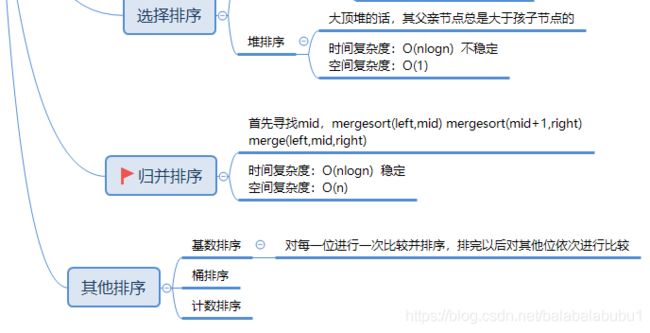
- 选择排序
-
-
-
其他难题
33、搜索旋转排序数组
解题思路: 该段排序由于从中间划分,因此,必有一段是有序的 首先寻找其mid值,并将target与mid比较,若相等则返回即可。
若不相等,则target可能存在于左区间或者右区间,且两个区间必有一个是有序的。 首先若左区间有序{
目标存在于该区间内,则按照二分查找算法搜索 目标不在该区间内,则目标在右区间内或者不存在,因此left=mid+1转战右区间
}否则(即右区间有序){ 目标存在于该区间内,则按照二分查找算法搜索
目标不在该区间内,则目标在左区间内或者不存在,因此right=mid-1转战左区间 }
int left=0,right=nums.length-1;
while(left<=right) {
int mid=left+(right-left)/2;
if(nums[mid]==target) return mid;
if(nums[0]<=nums[mid]) {//左半边有序
if(nums[0]<=target &&nums[mid]>target) {//目标值在左半边
right=mid-1;
}else {
left=mid+1;
}
}else {//右半边有序
if(nums[right]>=target &&nums[mid]5、最长回文子串
中心扩散法
//中心扩散法
//index从0开始,记录最长子串
if(s.length()==0) return "";
if(s.length()==1) return s;
int startIndex=0,maxLength=0;
for(int i=0;i0)&&(s.charAt(left)==s.charAt(i))) {
left--;
}
while((right<=s.length()-1)&&(s.charAt(right)==s.charAt(i))) {
right++;
}
//同时移动left和right,看两端是否相同,若相同,则变化left和right
while((left>=0)&&(right<=s.length()-1)&&(s.charAt(left)==s.charAt(right))) {
left--;
right++;
}
left++;
right--;
if(right-left+1>maxLength) {
maxLength=right-left+1;
startIndex=left;
}
}
return s.substring(startIndex, startIndex+maxLength);
递归
最大公约数
public static int count(int m,int n){
if(m%n==0) return n;
else{
return count(n,m%n);
}
}
二叉搜索树的范围和 938
//递归
class Solution {
public int rangeSumBST(TreeNode root, int L, int R) {
if(root==null) return 0; //若为空,返回0
//当root的值比L还要小,则(L,R)范围内可能存在的只有其右子树,返回右子树上的在该范围内的值
if(root.valR) return rangeSumBST(root.left,L,R);
//root符合标准,将root值加上以后再加上其左右子树返回过来的值
return root.val+rangeSumBST(root.left,L,R)+rangeSumBST(root.right,L,R);
}
}
递归乘法 面试题08.05
class Solution {
public int multiply(int A, int B) {
if(A==0 ||B==0) return 0;
return A+multiply(A,B-1);
}
}
二叉搜索树节点的最小距离 783
主要思路:对于二叉搜索树,其在中序遍历的时候是有序的,因此只需要不断记录在中序遍历时两个相邻节点的距离就可以得到最小距离
class Solution {
int min;
TreeNode pre;
public int minDiffInBST(TreeNode root) {
if(root==null ||(root.left==null &&root.right==null)) return 0;
//中序递归遍历
min=Integer.MAX_VALUE;
TreeNode pre=null;
dfs(root);
return min;
}
private void dfs(TreeNode root){
if(root ==null) return ;
dfs(root.left);
if(pre!=null){
min=Math.min(min,root.val-pre.val);
}
pre=root;
dfs(root.right);
}
}
最长同值路径 687 20200722
思路:递归
class Solution {
int max; //全局成员变量
public int longestUnivaluePath(TreeNode root) {
if(root==null||(root.left==null && root.right==null)) return 0;
max=Integer.MIN_VALUE;
dfs(root); //递归
return max;
}
private int dfs(TreeNode root){
if(root==null) return 0;
int left=dfs(root.left); //拿到该点左子树的高度,还不包括这个点
int right=dfs(root.right);//拿到该点右子树的高度,还不包括这个点
int arrleft=0;
int arrright=0;
//如果左节点的值与root相同,左子树高度+1
if(root.left!=null && root.val==root.left.val) arrleft+=(left+1);
//如果右节点的值与root相同,右子树高度+1
//贯穿一下
if(root.right!=null && root.val==root.right.val) arrright+=(right+1);
//max记录一下当前root的高度是否为最大,如果是的话,替换
max=Math.max(max,arrleft+arrright);
//但是该函数返回的时候,当前子树对父节点提供的最大长度为左右链中较大的一个
return Math.max(arrleft,arrright);
}
}
数值的整数次方
实现函数double Power(double base, int exponent),求base的exponent次方。不得使用库函数,同时不需要考虑大数问题。
示例 1:
输入: 2.00000, 10
输出: 1024.00000
class Solution {
public double myPow(double x, int n) {
if(x==0) return 0;
boolean flag=false;
double res=1.0;
long b=n;
if(b<0) {
x=1/x;
b=-b;
}
while(b>0){
if((b&1)==1) res*=x;
x=x*x;
b>>=1;
}
return res;
}
}
动态规划
礼物的最大价值
在一个 m*n 的棋盘的每一格都放有一个礼物,每个礼物都有一定的价值(价值大于 0)。你可以从棋盘的左上角开始拿格子里的礼物,并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值,请计算你最多能拿到多少价值的礼物?
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 12
解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物
class Solution {
public int maxValue(int[][] grid) {
int m=grid.length;
int n=grid[0].length;
int[][] res=new int[m][n];
res[0][0]=grid[0][0];
for(int i=1;i最小路径和
给定一个包含非负整数的 m x n 网格,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能向下或者向右移动一步。
示例:
输入:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
输出: 7
解释: 因为路径 1→3→1→1→1 的总和最小。
class Solution {
public int minPathSum(int[][] grid) {
if(grid.length==0) return 0;
int[][] res=new int[grid.length][grid[0].length];
res[0][0]=grid[0][0];
for(int i=1;i三角形最小路径和
给定一个三角形,找出自顶向下的最小路径和。每一步只能移动到下一行中相邻的结点上。
相邻的结点 在这里指的是 下标 与 上一层结点下标 相同或者等于 上一层结点下标 + 1 的两个结点。
例如,给定三角形:
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
自顶向下的最小路径和为 11(即,2 + 3 + 5 + 1 = 11)。
class Solution {
public int minimumTotal(List> triangle) {
int n=triangle.size();
int[][] res=new int[n][n];
res[0][0]=triangle.get(0).get(0);
for(int i=1;ires[n-1][i]) min=res[n-1][i];
}
return min;
}
}
买卖一次 股票的最大利润
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
class Solution {
public int maxProfit(int[] prices) {
if(prices.length==0) return 0;
int[] res=new int[prices.length];
int min=prices[0];
res[0]=0;
for(int i=1;i机器人路径问题
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。1. 向右 -> 向右 -> 向下2. 向右 -> 向下 -> 向右3. 向下 -> 向右 -> 向右
class Solution {
public int uniquePaths(int m, int n) {
int[][] res=new int[m][n];
for(int i=0;i有障碍物的机器人路径问题
class Solution {
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
if(obstacleGrid.length==0)return 0;
int m=obstacleGrid.length;
int n=obstacleGrid[0].length;
int[][] res=new int[m][n];
if(obstacleGrid[0][0]==1) return 0;
else{
res[0][0]=1;
for(int i=1;i完全平方数
给定正整数 n,找到若干个完全平方数(比如 1, 4, 9, 16, …)使得它们的和等于 n。你需要让组成和的完全平方数的个数最少。
示例 1:
输入: n = 12
输出: 3
解释: 12 = 4 + 4 + 4.
示例 2:
输入: n = 13
输出: 2
解释: 13 = 4 + 9.
class Solution {
public int numSquares(int n) {
int[] dp=new int[n+1];
for(int i=1;i<=n;i++) {
dp[i]=i;
for(int j=1;i-j*j>=0;j++) {
dp[i]=Math.min(dp[i], dp[i-j*j]+1);
}
}
return dp[n];
}
}
剪绳子
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
示例 1:
输入: 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1
示例 2:
输入: 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
class Solution {
public int cuttingRope(int n) {
if(n==0|n==1) return 0;
if(n==2) return 1;
if(n==3) return 2;
int[] dp=new int[n+1];
dp[0]=0;
dp[1]=0;
dp[2]=1;
dp[3]=2;
for(int i=4;i<=n;i++){
int res=0;
for(int j=1;j最长上升子序列
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
class Solution {
public int lengthOfLIS(int[] nums) {
if(nums.length<=1) return nums.length;
int[] res=new int[nums.length];
res[0]=1;
int max=1;
for(int i=1;imax) max=res[i];
}
return max;
}
}
判断子序列
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
你可以认为 s 和 t 中仅包含英文小写字母。字符串 t 可能会很长(长度 ~= 500,000),而 s 是个短字符串(长度 <=100)。
字符串的一个子序列是原始字符串删除一些(也可以不删除)字符而不改变剩余字符相对位置形成的新字符串。(例如,"ace"是"abcde"的一个子序列,而"aec"不是)。
class Solution {
public boolean isSubsequence(String s, String t) {
int s_index=0;
int t_index=0;
if(s.length()>t.length()) return false;
while(s_index回溯
技巧:
1、回溯用来解决组合问题
2、首先使用观察法观察结果集的子集排列顺序是否是有序的
【有序包括(1,2,3)(2,3)无序包括(2,1,3)(2,3,1)】
如果有序,无需设置辅助数据结构,但是递归函数中需要设置index值
如果无序,需要设置辅助数据结构,index一般要从头开始遍历
3、回溯法的主要节点在于“回”,即这一趟结束需要对刚添加进去的元素进行回退,以便进行下一次遍历
全排列 46
输入: [1,2,3]
输出:
[
[1,2,3],
[1,3,2],
[2,1,3],
[2,3,1],
[3,1,2],
[3,2,1]
]
分析:组合;无序;
Perms(nums[0-n-1])={取出一个数字}+Perms(nums[0-n-1]-这个数字)
import java.util.ArrayList;
import java.util.List;
public class Permute {
public List> permute(int[] nums) {
List> list =new ArrayList<>();
if(nums.length==0) return list;
if(nums.length==1) {
List res=new ArrayList<>();
res.add(nums[0]);
list.add(new ArrayList<>(res));
return list;
}
boolean[] isVisited =new boolean[nums.length];
List res=new ArrayList<>();
traceBack(nums,list,res,isVisited);
return list;
}
private void traceBack(int[] nums, List> list, List res, boolean[] isVisited) {
// TODO Auto-generated method stub
if(res.size()==nums.length) {
list.add(new ArrayList<>(res));
return ;
}
for(int i=0;i 全排列 II 47
解题思路:首先写出全排列基础版的算法,再进行思考剪枝
在有重复数字时,首先要考虑的是排序,再对剩下的算法进行剪枝处理
输入: [1,1,2]
输出:
[
[1,1,2],
[1,2,1],
[2,1,1]
]
class Solution {
public List> permuteUnique(int[] nums) {
List> list =new ArrayList<>();
if(nums.length==0) return list;
if(nums.length==1) {
List res=new ArrayList<>();
res.add(nums[0]);
list.add(res);
return list;
}
List res=new ArrayList<>();
boolean[] isVisited=new boolean[nums.length];
Arrays.sort(nums);
permuteDfs(nums,0,list,res,isVisited);
return list;
}
private void permuteDfs(int[] nums, int index, List> list, List res, boolean[] isVisited) {
// TODO Auto-generated method stub
if(res.size()==nums.length) {
for(int i=0;i(res));
return ;
}
for(int i=0;i0 && nums[i]==nums[i-1] && isVisited[i-1]) continue;
if(!isVisited[i]) {
res.add(nums[i]);
isVisited[i]=true;
permuteDfs(nums, i, list, res, isVisited);
res.remove(res.size()-1);
isVisited[i]=false;
}
}
}
}
分割回文串
输入: “aab”
输出:
[
[“aa”,“b”],
[“a”,“a”,“b”]
]
class Solution {
public List> partition(String s) {
List> res=new ArrayList<>();
if(s.length()==0) return res;
List list=new ArrayList<>();
backTrace(s,0,list,res);
return res;
}
private static void backTrace(String s,int index,List list,List> res){
if(s.length()==index){
res.add(new ArrayList<>(list));
return ;
}
for(int i=index;i 字符串生成
输入:s = “abc”
输出:[“abc”,“acb”,“bac”,“bca”,“cab”,“cba”]
class Solution {
public String[] permutation(String s) {
Set list=new HashSet();
boolean[] isVisited=new boolean[s.length()];
if(s.length()==0) return null;
perm(s,0,"",isVisited,list);
String[] resString =new String[list.size()];
Iterator it=list.iterator();
int i=0;
while(it.hasNext()) {
resString[i++]=it.next();
}
return resString;
}
private void perm(String s, int start, String res, boolean[] isVisited, Set list) {
// TODO Auto-generated method stub
if(res.length()==s.length()) {
list.add(res);
return ;
}
for(int i=0;i 括号生成
输入:n = 3
输出:[
“((()))”,
“(()())”,
“(())()”,
“()(())”,
“()()()”
]
class Solution {
public List generateParenthesis(int n) {
if(n==0) return new ArrayList<>(0); //n==0时直接return
List res=new ArrayList<>();
int left_len=0;
int right_len=0;
dfs(left_len,right_len,n,res,"");
return res;
}
private void dfs(int left_len, int right_len, int n, List res, String s) {
// TODO Auto-generated method stub
if(s.length()==2*n){ //递归结束条件
res.add(s);
return ;
}
if(left_len 子集78
输入: nums = [1,2,3]
输出:
[
[3],
[1],
[2],
[1,2,3],
[1,3],
[2,3],
[1,2],
[]
]
分析:组合,有序,长度不一样,需要传进去长度
class Solution {
public List> subsets(int[] nums) {
List> list =new ArrayList<>();
if(nums.length==0) return list;
list.add(new ArrayList<>());
List res=new ArrayList<>();
//从nums中取出的子集长度为1---n
for(int i=1;i<=nums.length;i++) {
backTrace(nums,i,0,res,list);
}
return list;
}
private void backTrace(int[] nums, int len, int index, List res, List> list) {
// res的长度等于len时,添加进list
if(res.size()==len) {
list.add(new ArrayList<>(res));
return;
}
//对于该循环,当将i添加进res后,由于有序,则后续再添加只考虑index值为i以后的元素
for(int i=index;i 复原ip地址 93
class Solution {
public List restoreIpAddresses(String s) {
List list =new ArrayList<>();
if(s.length()<4) return list;
restoreDfs(s,0,0,list,"");
return list;
}
private void restoreDfs(String s,int index,int count,List list,String res){
if(count==3 &&index3 ||index>=s.length()) return ;
for(int i=index;i2) break;
String subss=s.substring(index,i+1);
if(isValid(subss)){
res=res+s.substring(index,i+1)+'.';
restoreDfs(s,i+1,count+1,list,res);
res=res.substring(0,res.length()-(i-index+1)-1);
}
}
}
private boolean isValid(String subS){
if(subS.length()>3|| Integer.parseInt(subS)>255) return false;
if(subS.charAt(0)=='0' && subS.length()!=1) return false;
return true;
}
}
电话号码组合
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
class Main31 {
public List letterCombinations(String digits) {
HashMap map=new HashMap<>();
map.put('2',"abc");
map.put('3',"def");
map.put('4',"ghi");
map.put('5',"jkl");
map.put('6',"mno");
map.put('7',"pqrs");
map.put('8',"tuv");
map.put('9',"wxyz");
List list =new ArrayList<>();
String res="";
combitions(digits,list,res,0,map);
return list;
}
private void combitions(String digits,List list, String res, int index, HashMap map){
if(index==digits.length()){
list.add(res);
return ;
}
String ss=map.get(digits.charAt(index));
for(int i=0;i 组合总和
输入:candidates = [2,3,5], target = 8,
所求解集为:
[
[2,2,2,2],
[2,3,3],
[3,5]
]
import java.util.ArrayList;
import java.util.List;
public class Main32 {
public List> combinationSum(int[] candidates, int target) {
List> list=new ArrayList<>();
List res=new ArrayList<>();
dfsSum(candidates,0,target,list,res);
return list;
}
private void dfsSum(int[] candidates,int index, int target,List> list,List res){
if(target==0){
list.add(new ArrayList<>(res));
return;
}
if(target<0) return ;
for(int i=index;i 2
2 2
2 2 2
2 2 2 2
2 2 2 3
2 2 2 6
2 2 2 7
2 2 3
2 2 6
2 2 7
2 3
2 3 3
2 3 6
2 3 7
2 6
2 7
3
3 3
3 3 3
3 3 6
3 3 7
3 6
3 7
6
6 6
6 7
7
组合总和||
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
[1, 7],
[1, 2, 5],
[2, 6],
[1, 1, 6]
]
class Solution {
public List<List<Integer>> combinationSum2(int[] candidates, int target) {
if(candidates.length==0||target==0) return new ArrayList<>();
Arrays.sort(candidates);
List<List<Integer>> list=new ArrayList<>(); //记录所有结果
List<Integer> res=new ArrayList<>(); //记录该次的结果
backTrace(candidates,0,target,res,list);
return list;
}
private void backTrace(int[] candidates, int index, int target, List<Integer> res, List<List<Integer>> list) {
// TODO Auto-generated method stub
if(target==0){
list.add(new ArrayList<>(res));
return ;
}
if(target<0) return ;
for(int i=index;i<candidates.length;i++){
if(i>index && candidates[i]==candidates[i-1]) continue;//同一递归层不使用相同的元素
res.add(candidates[i]);
backTrace(candidates,i+1,target-candidates[i],res,list);
res.remove(res.size()-1);
}
}
}
单词搜索
board =
[
[‘A’,‘B’,‘C’,‘E’],
[‘S’,‘F’,‘C’,‘S’],
[‘A’,‘D’,‘E’,‘E’]
]
给定 word = “ABCCED”, 返回 true
给定 word = “SEE”, 返回 true
给定 word = “ABCB”, 返回 false
class Solution {
public boolean exist(char[][] board, String word) {
int row=board.length;
int col=board[0].length;
int[][] directions={{0,1},{1,0},{-1,0},{0,-1}};
boolean[][] isVisted=new boolean[row][col];
for(int i=0;i=0 &&i=0 &&j 复原ip地址
输入: “25525511135”
输出: [“255.255.11.135”, “255.255.111.35”]
class Solution {
public List restoreIpAddresses(String s) {
List list =new ArrayList<>();
if(s.length()<4) return list;
restoreDfs(s,0,0,list,"");
return list;
}
private void restoreDfs(String s,int index,int count,List list,String res){
if(count==3 &&index3 ||index>=s.length()) return ;
for(int i=index;i2) break;
String subss=s.substring(index,i+1);
if(isValid(subss)){
res=res+s.substring(index,i+1)+'.';
restoreDfs(s,i+1,count+1,list,res);
res=res.substring(0,res.length()-(i-index+1)-1);
}
}
}
private boolean isValid(String subS){
if(subS.length()>3|| Integer.parseInt(subS)>255) return false;
if(subS.charAt(0)=='0' && subS.length()!=1) return false;
return true;
}
}
简单
跳水板 面试题16.11
class Solution {
public int[] divingBoard(int shorter, int longer, int k) {
if(k==0) return new int[0];
int length=0;
if(shorter==longer) {
int[] res=new int[1];
res[0]=shorter*k;
return res;
}
int[] res=new int[k+1];
int deta=longer-shorter;
res[0]=shorter*k;
for(int i=1;i数组
区间合并
class Mycompare implements Comparator{
@Override
public int compare(int[] o1, int[] o2) {
// TODO Auto-generated method stub
return o1[0]-o2[0];
}
}
Scanner sc =new Scanner(System.in);
String[] s=sc.nextLine().split(" ");
int[][] nums=new int[s.length][2];
int i=0;
for(String ss:s){
nums[i][0]=Integer.parseInt(ss.split(",")[0]);
nums[i++][1]=Integer.parseInt(ss.split(",")[1]);
}
//Arrays.sort(nums,(a,b)->Integer.compare(a[0],b[0]));
// Comparator cp = new Comparator() {
//
// public int compare(int[] o1, int[] o2) {
// return o1[0]-o2[0];
// }
// };
Arrays.sort(nums,new Mycompare());
List list =new ArrayList<>();
for(int j=0;j 超过数组的一半的数
import java.util.*;
public class Solution {
public int MoreThanHalfNum_Solution(int [] array) {
HashMap map=new HashMap<>();
for(int i=0;i> it =map.entrySet().iterator();
while(it.hasNext()){
Map.Entry entry=it.next();
if(entry.getValue()>array.length/2)
{
res=entry.getKey();
break;
}
}
return res;
}
}
三数之和为0
给定数组 nums = [-1, 0, 1, 2, -1, -4],
满足要求的三元组集合为:
[
[-1, 0, 1],
[-1, -1, 2]
]
class Solution {
public List> threeSum(int[] nums) {
List> ans = new ArrayList();
int len = nums.length;
if(nums == null || len < 3) return ans;
Arrays.sort(nums); // 排序
for (int i = 0; i < len ; i++) {
if(nums[i] > 0) break; // 如果当前数字大于0,则三数之和一定大于0,所以结束循环
if(i > 0 && nums[i] == nums[i-1]) continue; // 去重
int L = i+1;
int R = len-1;
while(L < R){
int sum = nums[i] + nums[L] + nums[R];
if(sum == 0){
ans.add(Arrays.asList(nums[i],nums[L],nums[R]));
while (L 0) R--;
}
}
return ans;
}
}
字符串
s.length()
s.charAt();
s.substring(beginIndex,endIndex);
两个大数字符串求和输出字符串
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner sc =new Scanner(System.in);
while(sc.hasNextLine()){
String s=sc.nextLine();
String s1=s.split(",")[0];
String s2=s.split(",")[1];
if(s1.length()==0|s2.length()==0) System.out.println(0);else{
//判断其最大公共子串
int res=0;
for(int i=0;i符号配对,如{}为true,{[}为false
注:stack栈为空时stack.peek() 报错
stack常用方法:stack.push()/stack.pop()/stack.isEmpty()
import java.util.Scanner;
import java.util.Stack;
public class Main {
public static void main(String[] args) {
// TODO Auto-generated method stub
Scanner sc=new Scanner(System.in);
while(sc.hasNextLine()){
String s=sc.nextLine();
Stack stack=new Stack<>();
for(int i=0;i 排序
插入排序
//插入排序 稳定
//第一轮从第二个位置开始,若值比前面的有序数组小往前遍历
private void insertSort(int[] nums) {
for(int i=1;i=0;j--) {
if(nums[j]>num) {
nums[j+1]=nums[j];
}else {
break;
}
}
nums[j+1]=num;
}
}
冒泡排序
//冒泡排序 稳定
for(int i=nums.length-1;i>=0;i--) {
for(int j=0;jnums[j+1]) {
int temp=nums[j];
nums[j]=nums[j+1];
nums[j+1]=temp;
}
}
}
归并排序
//归并排序 稳定 递归写法
private static void mergeSort(int[] nums,int left,int right) {
if(left快速排序
//快速排序 不稳定 O(nlogn) 辅助空间 O(logn)~O(n)
public class quickSort {
public static void main(String[] args) {
int[] nums= {2,3,1,7,4,6,3};
quicksort(nums,0,nums.length-1);
for(int i:nums) System.out.println(i);
}
private static void quicksort(int[] nums, int left, int right) {
if(leftpivot) right--;
if(left 选择排序
//选择排序 不稳定,从小到大排序
//第一轮将第一个位置与遍历的剩下的位置比较,如果第一个位置大了就交换
//第二轮从第二个数组位置开始
for(int i=0;inums[j]) swap;
}
}