Siren论文阅读笔记：Implicit Neural Representations with Periodic Activation Functions具有周期激活函数的隐式神经表示

Implicit Neural Representations with Periodic Activation Functions

Title:具有周期激活函数的隐式神经表示

论文地址：论文地址arixv
https://arxiv.org/pdf/2006.09661v1.pdf

项目网址：项目地址
https://paperswithcode.com/paper/implicit-neural-representations-with-periodic

我的Github我的Github仓库 Siren_Study
https://github.com/QinghongShao-sqh/Siren_Study
Including my attempts to improve Siren, although the results were not ideal.

本文会对结合数学公式讲一下该篇文章，可以自行选择性观看

公众号：AI知识物语；B站暂定；知乎同名

---

插播：后面几个月我会慢慢更新我的Github，主要就是与博客相关的代码。目前已经开放了Nerf代码的仓库，其中包含大量的注解，可以方便初学者更快上手、理解，欢迎大家浏览，如果有帮助的话，可以给个Star，你的鼓励是我前进的最大动力！
Github链接如下
Nerf项目学习

摘要Abstract

由神经网络参数化的隐式定义的、连续的、可微的信号表示已经成为一种强大的范例，与传统的表示相比，它提供了许多可能的好处。 然而，当前用于此类隐式神经表示的网络架构无法对信号进行精细细节建模，并且无法表示信号的空间和时间导数，尽管事实上这些对于许多隐式定义为偏微分方程解的物理信号至关重要 。 我们建议利用周期性激活函数进行隐式神经表示，并证明这些网络（称为正弦表示网络或 SIREN）非常适合表示复杂的自然信号及其导数。 我们分析 SIREN 激活统计数据，提出一个原则性的初始化方案，并演示图像、波场、视频、声音及其导数的表示。 此外，我们还展示了如何利用 SIREN 来解决具有挑战性的边值问题，例如特定的 Eikonal 方程（产生有符号距离函数）、泊松方程以及亥姆霍兹方程和波动方程。 最后，我们将 SIREN 与超网络结合起来，学习 SIREN 函数空间的先验。 请参阅项目网站提供了所提出的方法和所有应用的视频概述。

个人理解：
Siren的主要特点是它能够产生平滑和连续的激活函数，这有助于解决传统神经网络中存在的棘手问题，如梯度消失和爆炸。Siren的激活函数定义为f(x) = sin(w * x)，其中w是可学习的参数。通过使用正弦函数，Siren能够实现周期性的变化，并且能够逼近任意函数。

Siren在图像生成、物体形状表示等领域展示了出色的性能，并且在生成高质量图像和形状时表现出了优势。它已经引起了广泛的关注，并且在深度学习领域中被广泛应用。

1.介绍Introduction

我们感兴趣的是一类满足 F 形式方程的函数 Φ

该隐式问题公式将空间或时空坐标 x ∈ Rm 以及可选的 Φ 相对于这些坐标的导数作为输入。 我们的目标是学习一个神经网络，该神经网络对 Φ 进行参数化，以将 x 映射到某个感兴趣的量，同时满足等式（1）中提出的约束。

因此，Φ 由 F 定义的关系隐式定义，我们将这种隐式定义的函数参数化的神经网络称为隐式神经表示。 正如我们在本文中所展示的，跨科学领域的各种问题都属于这种形式，例如使用连续和可微的表示对图像、视频和音频处理中许多不同类型的离散信号进行建模，通过学习 3D 形状表示 有符号距离函数 [1-4]，更一般地说，解决边值问题，例如泊松，亥姆霍兹或波动方程。

与替代方案（例如基于离散网格的表示）相比，连续参数化具有多种优势。 例如，由于 Φ 是在 x 的连续域上定义的，因此它比离散表示具有更高的内存效率，从而允许它建模不受网格分辨率限制而是受网格容量限制的精细细节。 底层网络架构。 可微分意味着可以分析计算梯度和高阶导数，例如使用自动微分，这再次使这些模型独立于传统的网格分辨率。 最后，通过良好的导数，隐式神经表示可以为解决反问题（例如微分方程）提供新的工具箱。

由于这些原因，隐式神经表征在去年引起了广泛的研究兴趣（第 2 节）。 大多数最近的表示都建立在基于 ReLU 的多层感知器 (MLP) 之上。 虽然很有希望，但这些架构缺乏表示底层信号中的精细细节的能力，并且它们通常不能很好地表示目标信号的导数。 部分原因是 ReLU 网络是分段线性的，其二阶导数处处为零，因此无法对自然信号高阶导数中包含的信息进行建模。 虽然替代激活（例如 tanh 或 softplus）能够表示高阶导数，但我们证明它们的导数通常表现不佳，也无法表示精细细节。 为了解决这些限制，我们利用具有周期性激活函数的 MLP 来实现隐式神经表示。 我们证明，这种方法不仅能够比 ReLU-MLP 或并行工作 [5] 中提出的位置编码策略更好地表示信号中的细节，而且这些属性也独特地适用于导数，这对于许多应用来说至关重要我们在本文中进行探索。

2.贡献Contribution

• 使用周期性激活函数的连续隐式神经表示，可以稳健地拟合复杂信号，例如自然图像和3D 形状及其导数。（提出周期性激活函数）
• 用于训练这些表示并验证可以使用超网络学习这些表示的分布的初始化方案。 （网络初始化方案）
• 应用演示：图像、视频和音频表示； 3D形状重建； 求解旨在估计信号的一阶微分方程仅用其梯度进行监督； 并求解二阶微分方程。

3.Formulation 方法/公式

Step1

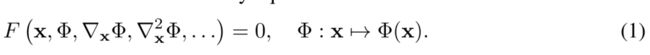
这个方程1：
（1） 输入：时空坐标 x ∈ Rm 以及可选的 Φ 相对于这些坐标的导数
（2）Φ可以理解为多层感知器
（3）Φ满足的约束（条件）如方程1，也就是 输入x，Φ一阶导，Φ二阶导等，要满足函数F为0，也就是满足这个条件、约束。
在神经网络里面，也就是训练参数Φ，使得参数Φ 可以拟合上面的方程，也就是尽可能满足方程一的这个约束表达

Step2

我们的目标是解决方程（1）所示形式的问题。 我们将此视为一个可行性问题，其中寻求满足一组 M 约束（如下）:
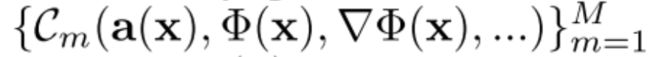其中每一个都将函数 Φ 和/或其导数与量 a(x)：
根据 Cm 求 Φ(x)

方程2：
（1）前提，方程2成立的条件是其要满足约束M，也就是上述提到的Cm
（2）约束条件也就是 C_m(参数1，参数2，-----) = 0


这个问题可以用损失函数来表示，该函数惩罚偏离域 Ωm 上每个约束的偏差：

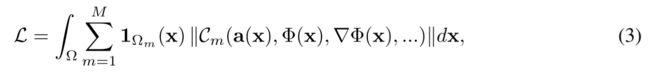
在实践中，损失函数通过采样 Ω 来强制执行。 数据集 D = {(xi, ai(x))}i 是一组坐标 xi ∈ Ω 的元组以及约束中出现的量 a(xi) 的样本。 因此，等式（3）中的损失强制作用于从数据集中采样的坐标 xi 上，产生损失

实际上，对数据集 D 进行采样在训练时动态地进行，随着样本数量的增长更好地逼近 L，如蒙特卡洛积分。

我们将函数 Φθ 参数化为具有参数 θ 的全连接神经网络，并求解使用梯度下降产生的优化问题。

方程3：
（1）为了找到比较好的Φ（x）值，使得其可以优秀地拟合Cm函数（网络），设计了一个loss损失函数
（2）通过最小化这个损失函数，模型可以学习到满足约束函数的输出。这有助于优化隐式神经表示，使其能够更好地捕捉输入数据的周期性结构。

3.1 隐式神经表示的周期性激活

我们提出了 SIREN，一种用于隐式神经表示的简单神经网络架构，它使用正弦作为周期性激活函数：

方程3：
（1）神经网络设为n层layer ，每层线性层计算操作为W_i * x_i + b_i ，并添加sin操作
（2）第0 到n-1层，操作 线性操作 + 激活 （最后层不加激活，避免值域错误）

这里， φi : RMi → RNi 是网络的第 i 层。 它由权重矩阵 Wi ∈ RNi×Mi 定义的仿射变换组成，
以及通过应用于结果向量的每个分量的正弦非线性将偏差 bi ∈ RNi 应用于输入 xi ∈ RMi。

有趣的是，SIREN 的任何导数本身就是 SIREN，因为正弦的导数是余弦，即相移正弦（参见补充）。

因此，SIREN 的导数继承了 SIREN 的属性，使我们能够用“复杂”信号来监督 SIREN 的任何导数。 在我们的实验中，我们证明，当使用涉及 φ 导数的约束 Cm 来监督 SIREN 时，函数 φ 仍然表现良好，这对于解决许多问题（包括边值问题 (BVP)）至关重要。

我们将展示 SIREN 可以通过对激活分布的一些控制来初始化，从而使我们能够创建深层架构。 此外，SIREN 的收敛速度明显快于基线架构，例如，在数百次迭代中拟合单个图像，需要花费一些时间在现代 GPU 上只需几秒，同时具有更高的图像保真度（图 1）。

3.2 激活、频率的分布和有原则的初始化方案

我们提出了有效训练 SIREN 所必需的有原则的初始化方案。 虽然在这里非正式地介绍，但我们在补充材料中讨论了更多细节、证明和经验验证。 我们初始化方案的关键思想是通过网络保留激活的分布，以便初始化时的最终输出不依赖于层数。

因此，我们建议用 c = 6 来绘制权重，使得
$$w_i-U（-\sqrt{6/n}，\sqrt{6/n}）$$

这确保了每个正弦激活的输入都是正态分布，标准差为 1。由于只有少数权重的大小大于 π，因此整个正弦网络的频率增长缓慢。

最后，我们建议用权重初始化正弦网络的第一层，以便正弦函数
$$sin({\omega }_0\cdot W_x+b)$$
跨越 [−1, 1] 上的多个周期。
我们发现$${\omega }_0=30$$适合本工作中的所有应用。 所提出的初始化方案产生快速且鲁棒的
本工作中的所有实验均使用 ADAM 优化器进行收敛。

4.结果/比较 Results

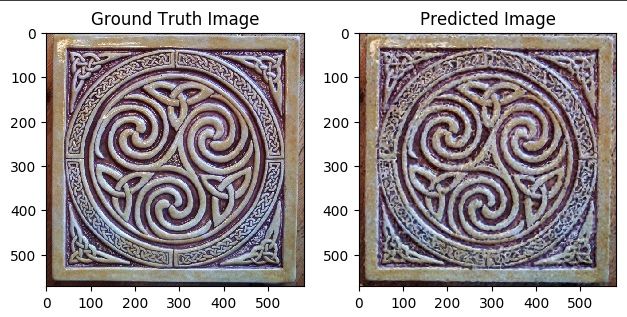
图 1：拟合地面实况图像的不同隐式网络架构的比较（左上）。 该表示仅在目标图像上进行监督，但我们还分别在第 2 行和第 3 行中显示了函数拟合的一阶和二阶导数。
总结：Siren激活函数的条件下，就算经过了求导，其依旧可以比较好的表征图片的细节特征等等。

图 2：使用 SIREN 和 ReLU-MLP 拟合视频的示例帧。 我们的方法忠实地重建了胡须等精细细节。 平均值（和标准差）报告所有帧的 PSNR。
总结：Siren拟合后的视频从上述结果，可以看到峰值信噪比更好。

图 3：泊松图像重建：通过拟合 SIREN 重建图像（左），并通过其梯度或拉普拉斯算子（绿色下划线）进行监督。 结果分别显示在中间和右侧，与图像及其导数很好地匹配。 泊松图像编辑：两个图像（上）的梯度被融合（左下）。 SIREN 允许复合材料（右）使用梯度监督重建（右下）。

图 4：形状表示。 我们直接在点云上拟合由隐式神经表示参数化的有符号距离函数。 与 ReLU 隐式表示相比，我们的周期激活显着改善了对象的细节（左）和整个场景的复杂性（右）。

5.代码Code

简单的Demo

# defining the model
layers = [256, 256, 256, 256, 256]
in_features = 2
out_features = 3
initializer = 'siren'
w0 = 1.0
w0_initial = 30.0
c = 6
model = SIREN(
    layers, in_features, out_features, w0, w0_initial,
    initializer=initializer, c=c)

# defining the input
x = torch.rand(10, 2)

# forward pass
y = model(x)

网络结构

SIREN(
  (network): Sequential(
    (0): Linear(in_features=2, out_features=256, bias=True)
    (1): Sine()
    (2): Linear(in_features=256, out_features=256, bias=True)
    (3): Sine()
    (4): Linear(in_features=256, out_features=256, bias=True)
    (5): Sine()
    (6): Linear(in_features=256, out_features=256, bias=True)
    (7): Sine()
    (8): Linear(in_features=256, out_features=256, bias=True)
    (9): Sine()
    (10): Linear(in_features=256, out_features=3, bias=True)
  )
)
Input （x）
tensor([[0.2308, 0.3548],
        [0.5164, 0.6143],
        [0.6968, 0.8699],
        [0.6310, 0.5026],
        [0.4632, 0.5294],
        [0.0767, 0.8768],
        [0.4488, 0.4516],
        [0.6168, 0.3680],
        [0.3963, 0.1908],
        [0.8118, 0.0960]])

Output （y）
tensor([[-0.8706,  0.2084,  0.4391],
        [ 1.5811,  0.8201, -1.3626],
        [ 1.0847,  1.0457,  0.4729],
        [-1.1709,  0.4763, -0.8895],
        [ 0.2296, -1.1874,  0.0173],
        [-0.7613,  0.4856,  0.3994],
        [-0.6881,  1.1495, -1.7198],
        [ 0.1872, -0.3740, -0.4221],
        [-0.7435,  0.1381,  0.6936],
        [ 0.2644,  0.5492, -0.4556]], grad_fn=<AddmmBackward0>)

Siren网络结构

class SIREN(nn.Module):
    def __init__(self, layers: List[int], in_features: int,
                 out_features: int,
                 w0: float = 1.0,
                 w0_initial: float = 30.0,
                 bias: bool = True,
                 initializer: str = 'siren',
                 c: float = 6):
        """
	     :param layers: 每个隐藏层中的神经元数的列表
	    :type layers: List[int]
	    :param in_features: 输入特征的数量
	    :type in_features: int
	    :param out_features: 最终输出特征的数量
	    :type out_features: int
	    :param w0: 激活函数中的w0值 `act(x; w0) = sin(w0 * x)`。默认为1.0
	    :type w0: float, optional
	    :param w0_initial: 第一层的 `w0`。默认为30（与论文中使用的值相同）
	    :type w0_initial: float, optional
	    :param bias: 是否使用偏置。默认为True
	    :type bias: bool, optional
	    :param initializer: 指定使用的初始化方法。默认为'siren'
	    :type initializer: str, optional
	    :param c: 用于计算siren初始化器中的边界值。默认为6
	    :type c: float, optional
        """
        super(SIREN, self).__init__()
        self._check_params(layers)
        self.layers = [nn.Linear(in_features, layers[0], bias=bias), Sine(
            w0=w0_initial)]

        for index in range(len(layers) - 1):
            self.layers.extend([
                nn.Linear(layers[index], layers[index + 1], bias=bias),
                Sine(w0=w0)
            ])

        self.layers.append(nn.Linear(layers[-1], out_features, bias=bias))
        self.network = nn.Sequential(*self.layers)

        if initializer is not None and initializer == 'siren':
            for m in self.network.modules():
                if isinstance(m, nn.Linear):
                    siren_uniform_(m.weight, mode='fan_in', c=c)

    @staticmethod
    def _check_params(layers):
        assert isinstance(layers, list), 'layers should be a list of ints'
        assert len(layers) >= 1, 'layers should not be empty'

    def forward(self, X):
        return self.network(X)

上图是使用Siren神经网络生成图片的前后对比图