【Matlab】基于遗传算法优化 BP 神经网络的时间序列预测（Excel可直接替换数据）

1.模型原理

当遗传算法用于优化BP神经网络的时间序列预测时，我们可以使用如下的数学原理来描述其步骤：

1. 定义问题：
   假设我们有一个时间序列数据集 $\{(x_1,y_1),(x_2,y_2),\dots ,(x_n,y_n)\}$，其中 $x_i$ 是时间步i的输入样本，$y_i$ 是对应的时间步i的目标值（实际输出）。时间序列预测任务的目标是根据过去的观测值预测未来的值。

2. BP神经网络结构：
   假设BP神经网络有L层，第l层有 $n_l$ 个神经元。$w_{ij}^{(l)}$ 表示第l-1层第i个神经元到第l层第j个神经元之间的连接权重，$b_i^{(l)}$ 表示第l层第i个神经元的偏置。神经网络的输入是 $x_i$，第l层第i个神经元的输出（经过激活函数后的值）为 $a_i^{(l)}$。

3. 目标函数：
   在时间序列预测问题中，我们可以使用均方误差（Mean Squared Error，MSE）作为BP神经网络的目标函数，用于衡量实际输出值与预测输出值之间的差距。MSE可以定义为：

   $$\text{MSE}=\frac{1}{n}\sum _{i=1}^n(y_i-{\hat{y}}_i{)}^2$$

   其中，$n$是时间序列的长度，$y_i$是第i个时间步的实际输出，${\hat{y}}_i$是BP神经网络在输入 $x_i$ 上的预测输出。

4. 遗传算法编码：
   同样地，我们将BP神经网络的所有参数（权重和偏置）编码成一个染色体，通常用一个长向量来表示。染色体可以表示为：

   $$\text{染色体}=[w_{11}^{(1)},w_{12}^{(1)},\dots ,w_{n_1^{(1)}}^{(1)},w_{11}^{(2)},w_{12}^{(2)},\dots ,w_{n_{L-1}^{(L)}}^{(L)},b_1^{(1)},b_2^{(1)},\dots ,b_{n_1^{(L)}}^{(L)}]$$

   其中，$w_{ij}^{(l)}$ 表示第l-1层第i个神经元到第l层第j个神经元之间的连接权重，$b_i^{(l)}$ 表示第l-1层第i个神经元的偏置。

5. 适应度函数：
   在时间序列预测问题中，适应度函数可以定义为目标函数MSE的倒数（加上一个常数，以避免除以0）：

   $$\text{适应度}=\frac{1}{\text{MSE}+ϵ}$$

   其中，$ϵ$ 是一个小的常数，用于避免分母为0的情况。

6. 选择：
   采用基于适应度函数的选择策略，选择适应度较高的个体作为“父代”，用于产生下一代个体。

7. 交叉（Crossover）：
   对选出的父代个体进行交叉操作，通过模拟基因交换过程，生成新的个体。假设选中的两个父代个体分别为个体A和个体B，交叉操作可以通过如下方式进行：

   $$\text{子代个体}=[A[1:k],B[k+1:end]]$$

   其中，$A[1:k]$ 表示个体A的前k个基因，$B[k+1:end]$ 表示个体B的第k+1个基因到最后一个基因。

8. 变异（Mutation）：
   对交叉得到的子代个体进行变异操作，通过随机改变染色体中的某些基因值来引入新的解。变异操作可以用如下方式实现：

   $$\text{子代个体}[i]=\text{子代个体}[i]+\text{随机增量}$$

   其中，$\text{子代个体}[i]$ 表示子代个体中的第i个基因，$\text{随机增量}$ 是一个随机数，用于在某个范围内调整基因的值。

9. 生成下一代种群：
   将交叉和变异得到的子代个体与上一代的个体结合，形成下一代种群。

10. 终止条件：
    根据预定的终止条件（如迭代次数、达到某个适应度阈值等），判断是否结束优化过程。

11. 解码：
    将优化后的染色体解码，得到BP神经网络的新参数。

12. 更新BP神经网络参数：
    将解码得到的新参数应用于BP神经网络，更新其权重和偏置。

13. 重复迭代：
    重复进行步骤5到步骤12，直到满足终止条件为止。

2.文件结构

goat
	arithXover.m
	delta.m
	ga.m
	gabpEval.m
	initializega.m
	maxGenTerm.m
	nonUnifMutation.m
	normGeomSelect.m
	parse.m
gadecod.m
main.m							% 主函数
数据集.xlsx						% 可替换数据集

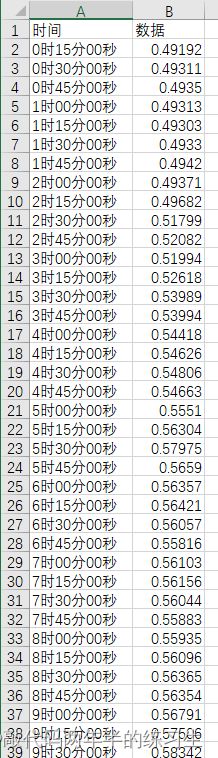
3.Excel数据

4.分块代码

4.1 arithXover.m

function [C1, C2] = arithXover(P1, P2, ~, ~)
%%  Arith 交叉采用两个父节点 P1、P2 并沿两个父节点形成的线执行插值。
% P1      - the first parent ( [solution string function value] )
% P2      - the second parent ( [solution string function value] )
% bounds  - the bounds matrix for the solution space
% Ops     - Options matrix for arith crossover [gen #ArithXovers]

%%  选择一个随机的混合量
a = rand;

%%  创建子代
C1 = P1 * a + P2 * (1 - a);
C2 = P1 * (1 - a) + P2 * a;

4.2 delta.m

function change = delta(ct, mt, y, b)

% delta 函数是非均匀突变使用的非均匀分布。
% 此函数根据当前发电量、最大发电量和可能的偏差量返回变化。
%
% ct - current generation
% mt - maximum generation
% y  - maximum amount of change, i.e. distance from parameter value to bounds
% b  - shape parameter

%%  
r = ct / mt;
if(r > 1)
  r = 0.99;
end
change = y * (rand * (1 - r)) ^ b;

4.3 ga.m

function [x, endPop, bPop, traceInfo] = ga(bounds, evalFN, evalOps, startPop, opts, ...
termFN, termOps, selectFN, selectOps, xOverFNs, xOverOps, mutFNs, mutOps)
                              
% Output Arguments:
%   x            - the best solution found during the course of the run
%   endPop       - the final population 
%   bPop         - a trace of the best population
%   traceInfo    - a matrix of best and means of the ga for each generation
%
% Input Arguments:
%   bounds       - a matrix of upper and lower bounds on the variables
%   evalFN       - the name of the evaluation .m function
%   evalOps      - options to pass to the evaluation function ([NULL])
%   startPop     - a matrix of solutions that can be initialized
%                  from initialize.m
%   opts         - [epsilon prob_ops display] change required to consider two 
%                  solutions different, prob_ops 0 if you want to apply the
%                  genetic operators probabilisticly to each solution, 1 if
%                  you are supplying a deterministic number of operator
%                  applications and display is 1 to output progress 0 for
%                  quiet. ([1e-6 1 0])
%   termFN       - name of the .m termination function (['maxGenTerm'])
%   termOps      - options string to be passed to the termination function
%                  ([100]).
%   selectFN     - name of the .m selection function (['normGeomSelect'])
%   selectOpts   - options string to be passed to select after
%                  select(pop,#,opts) ([0.08])
%   xOverFNS     - a string containing blank seperated names of Xover.m
%                  files (['arithXover heuristicXover simpleXover']) 
%   xOverOps     - A matrix of options to pass to Xover.m files with the
%                  first column being the number of that xOver to perform
%                  similiarly for mutation ([2 0;2 3;2 0])
%   mutFNs       - a string containing blank seperated names of mutation.m 
%                  files (['boundaryMutation multiNonUnifMutation ...
%                           nonUnifMutation unifMutation'])
%   mutOps       - A matrix of options to pass to Xover.m files with the
%                  first column being the number of that xOver to perform
%                  similiarly for mutation ([4 0 0;6 100 3;4 100 3;4 0 0])

%%  初始化参数
n = nargin;
if n < 2 || n == 6 || n == 10 || n == 12
  disp('Insufficient arguements') 
end

% 默认评估选项
if n < 3 
  evalOps = [];
end

% 默认参数
if n < 5
  opts = [1e-6, 1, 0];
end

% 默认参数
if isempty(opts)
  opts = [1e-6, 1, 0];
end

%%  判断是否为m文件
if any(evalFN < 48)
  % 浮点数编码 
  if opts(2) == 1
    e1str = ['x=c1; c1(xZomeLength)=', evalFN ';'];  
    e2str = ['x=c2; c2(xZomeLength)=', evalFN ';']; 
  % 二进制编码
  else
    e1str = ['x=b2f(endPop(j,:),bounds,bits); endPop(j,xZomeLength)=', evalFN ';'];
  end
else
  % 浮点数编码
  if opts(2) == 1
    e1str = ['[c1 c1(xZomeLength)]=' evalFN '(c1,[gen evalOps]);'];  
    e2str = ['[c2 c2(xZomeLength)]=' evalFN '(c2,[gen evalOps]);'];
  % 二进制编码
  else
    e1str=['x=b2f(endPop(j,:),bounds,bits);[x v]=' evalFN ...
	'(x,[gen evalOps]); endPop(j,:)=[f2b(x,bounds,bits) v];'];  
  end
end

%%  默认终止信息
if n < 6
  termOps = 100;
  termFN = 'maxGenTerm';
end

%%  默认变异信息
if n < 12
  % 浮点数编码
  if opts(2) == 1
  mutFNs = 'boundaryMutation multiNonUnifMutation nonUnifMutation unifMutation';
    mutOps = [4, 0, 0; 6, termOps(1), 3; 4, termOps(1), 3;4, 0, 0];
  % 二进制编码
  else
    mutFNs = 'binaryMutation';
    mutOps = 0.05;
  end
end

%%  默认交叉信息
if n < 10
  % 浮点数编码
  if opts(2) == 1
    xOverFNs = 'arithXover heuristicXover simpleXover';
    xOverOps = [2, 0; 2, 3; 2, 0];
  % 二进制编码
  else
    xOverFNs = 'simpleXover';
    xOverOps = 0.6;
  end
end

%%  仅默认选择选项，即轮盘赌。
if n < 9
  selectOps = [];
end

%%  默认选择信息
if n < 8
  selectFN = 'normGeomSelect';
  selectOps = 0.08;
end

%%  默认终止信息
if n < 6
  termOps = 100;
  termFN = 'maxGenTerm';
end

%%  没有定的初始种群
if n < 4
  startPop = [];
end

%%  随机生成种群
if isempty(startPop)
  startPop = initializega(80, bounds, evalFN, evalOps, opts(1: 2));
end

%%  二进制编码
if opts(2) == 0
  bits = calcbits(bounds, opts(1));
end

%%  参数设置
xOverFNs     = parse(xOverFNs);
mutFNs       = parse(mutFNs);
xZomeLength  = size(startPop, 2); 	          % xzome 的长度
numVar       = xZomeLength - 1; 	          % 变量数
popSize      = size(startPop,1); 	          % 种群人口个数
endPop       = zeros(popSize, xZomeLength);   % 第二种群矩阵
numXOvers    = size(xOverFNs, 1);             % Number of Crossover operators
numMuts      = size(mutFNs, 1); 		      % Number of Mutation operators
epsilon      = opts(1);                       % Threshold for two fittness to differ
oval         = max(startPop(:, xZomeLength)); % Best value in start pop
bFoundIn     = 1; 			                  % Number of times best has changed
done         = 0;                             % Done with simulated evolution
gen          = 1; 			                  % Current Generation Number
collectTrace = (nargout > 3); 		          % Should we collect info every gen
floatGA      = opts(2) == 1;                  % Probabilistic application of ops
display      = opts(3);                       % Display progress 

%%  精英模型
while(~done)
  [bval, bindx] = max(startPop(:, xZomeLength));            % Best of current pop
  best =  startPop(bindx, :);
  if collectTrace
    traceInfo(gen, 1) = gen; 		                        % current generation
    traceInfo(gen, 2) = startPop(bindx,  xZomeLength);      % Best fittness
    traceInfo(gen, 3) = mean(startPop(:, xZomeLength));     % Avg fittness
    traceInfo(gen, 4) = std(startPop(:,  xZomeLength)); 
  end
  
  %%  最佳解
  if ( (abs(bval - oval) > epsilon) || (gen==1))
    
    % 更新显示
    if display
      fprintf(1, '\n%d %f\n', gen, bval);          
    end

    % 更新种群矩阵
    if floatGA
      bPop(bFoundIn, :) = [gen, startPop(bindx, :)]; 
    else
      bPop(bFoundIn, :) = [gen, b2f(startPop(bindx, 1 : numVar), bounds, bits)...
	  startPop(bindx, xZomeLength)];
    end

    bFoundIn = bFoundIn + 1;                      % Update number of changes
    oval = bval;                                  % Update the best val
  else
    if display
      fprintf(1,'%d ',gen);	                      % Otherwise just update num gen
    end
  end
%%  选择种群
  endPop = feval(selectFN, startPop, [gen, selectOps]);
  
  % 以参数为操作数的模型运行
  if floatGA
    for i = 1 : numXOvers
      for j = 1 : xOverOps(i, 1)
          a = round(rand * (popSize - 1) + 1); 	     % Pick a parent
	      b = round(rand * (popSize - 1) + 1); 	     % Pick another parent
	      xN = deblank(xOverFNs(i, :)); 	         % Get the name of crossover function
	      [c1, c2] = feval(xN, endPop(a, :), endPop(b, :), bounds, [gen, xOverOps(i, :)]);

          % Make sure we created a new 
          if c1(1 : numVar) == endPop(a, (1 : numVar)) 
	         c1(xZomeLength) = endPop(a, xZomeLength);
	      elseif c1(1:numVar) == endPop(b, (1 : numVar))
	         c1(xZomeLength) = endPop(b, xZomeLength);
          else
             eval(e1str);
          end

          if c2(1 : numVar) == endPop(a, (1 : numVar))
	          c2(xZomeLength) = endPop(a, xZomeLength);
	      elseif c2(1 : numVar) == endPop(b, (1 : numVar))
	          c2(xZomeLength) = endPop(b, xZomeLength);
          else
	          eval(e2str);
          end

          endPop(a, :) = c1;
          endPop(b, :) = c2;
      end
    end

    for i = 1 : numMuts
      for j = 1 : mutOps(i, 1)
          a = round(rand * (popSize - 1) + 1);
          c1 = feval(deblank(mutFNs(i, :)), endPop(a, :), bounds, [gen, mutOps(i, :)]);
          if c1(1 : numVar) == endPop(a, (1 : numVar)) 
              c1(xZomeLength) = endPop(a, xZomeLength);
          else
              eval(e1str);
          end
          endPop(a, :) = c1;
      end
    end

%%  运行遗传算子的概率模型
  else 
    for i = 1 : numXOvers
        xN = deblank(xOverFNs(i, :));
        cp = find((rand(popSize, 1) < xOverOps(i, 1)) == 1);

        if rem(size(cp, 1), 2) 
            cp = cp(1 : (size(cp, 1) - 1)); 
        end
        cp = reshape(cp, size(cp, 1) / 2, 2);

        for j = 1 : size(cp, 1)
            a = cp(j, 1); 
            b = cp(j, 2); 
            [endPop(a, :), endPop(b, :)] = feval(xN, endPop(a, :), endPop(b, :), ...
                bounds, [gen, xOverOps(i, :)]);
        end
    end

    for i = 1 : numMuts
        mN = deblank(mutFNs(i, :));
        for j = 1 : popSize
            endPop(j, :) = feval(mN, endPop(j, :), bounds, [gen, mutOps(i, :)]);
            eval(e1str);
        end
    end

  end
  
  %  更新记录
  gen = gen + 1;
  done = feval(termFN, [gen, termOps], bPop, endPop); % See if the ga is done
  startPop = endPop; 			                      % Swap the populations
  [~, bindx] = min(startPop(:, xZomeLength));         % Keep the best solution
  startPop(bindx, :) = best; 		                  % replace it with the worst
  
end
[bval, bindx] = max(startPop(:, xZomeLength));

%%  显示结果
if display 
  fprintf(1, '\n%d %f\n', gen, bval);	  
end

%%  二进制编码
x = startPop(bindx, :);
if opts(2) == 0
  x = b2f(x, bounds,bits);
  bPop(bFoundIn, :) = [gen, b2f(startPop(bindx, 1 : numVar), bounds, bits)...
      startPop(bindx, xZomeLength)];
else
  bPop(bFoundIn, :) = [gen, startPop(bindx, :)];
end

%%  赋值
if collectTrace
  traceInfo(gen, 1) = gen; 		                      % 当前迭代次数
  traceInfo(gen, 2) = startPop(bindx, xZomeLength);   % 最佳适应度
  traceInfo(gen, 3) = mean(startPop(:, xZomeLength)); % 平均适应度
end

4.4 gabpEval.m

function [sol, val] = gabpEval(sol, ~)

%%  解码适应度值
val = gadecod(sol);

4.5 initializega.m

function pop = initializega(num, bounds, evalFN, evalOps, options)

%%  种群初始化
%    initializega creates a matrix of random numbers with 
%    a number of rows equal to the populationSize and a number
%    columns equal to the number of rows in bounds plus 1 for
%    the f(x) value which is found by applying the evalFN.
%    This is used by the ga to create the population if it
%    is not supplied.
%
% pop            - the initial, evaluated, random population 
% populatoinSize - the size of the population, i.e. the number to create
% variableBounds - a matrix which contains the bounds of each variable, i.e.
%                  [var1_high var1_low; var2_high var2_low; ....]
% evalFN         - the evaluation fn, usually the name of the .m file for 
%                  evaluation
% evalOps        - any options to be passed to the eval function defaults []
% options        - options to the initialize function, ie. 
%                  [type prec] where eps is the epsilon value 
%                  and the second option is 1 for float and 0 for binary, 
%                  prec is the precision of the variables defaults [1e-6 1]

%%  参数初始化
if nargin < 5
  options = [1e-6, 1];
end
if nargin < 4
  evalOps = [];
end

%%  编码方式
if any(evalFN < 48)    % M文件
  if options(2) == 1   % 浮点数编码
    estr = ['x=pop(i,1); pop(i,xZomeLength)=', evalFN ';'];  
  else                 % 二进制编码
    estr = ['x=b2f(pop(i,:),bounds,bits); pop(i,xZomeLength)=', evalFN ';']; 
  end
else                   % 非M文件
  if options(2) == 1   % 浮点数编码
    estr = ['[ pop(i,:) pop(i,xZomeLength)]=' evalFN '(pop(i,:),[0 evalOps]);']; 
  else                 % 二进制编码
    estr = ['x=b2f(pop(i,:),bounds,bits);[x v]=' evalFN ...
	'(x,[0 evalOps]); pop(i,:)=[f2b(x,bounds,bits) v];'];  
  end
end

%%  参数设置 
numVars = size(bounds, 1); 		           % 变量数
rng     = (bounds(:, 2) - bounds(:, 1))';  % 可变范围

%%  编码方式
if options(2) == 1               % 二进制编码
  xZomeLength = numVars + 1; 	 % 字符串的长度是 numVar + fit
  pop = zeros(num, xZomeLength); % 分配新种群
  pop(:, 1 : numVars) = (ones(num, 1) * rng) .* (rand(num, numVars)) + ...
    (ones(num, 1) * bounds(:, 1)');
else                             % 浮点数编码
  bits = calcbits(bounds, options(1));
  pop = round(rand(num, sum(bits) + 1));
end

%%  运行文件
for i = 1 : num
  eval(estr);
end

4.6 maxGenTerm.m

function done = maxGenTerm(ops, ~, ~)
% 返回 1，即当达到 maximal_generation 时终止 GA。
%
% ops    - a vector of options [current_gen maximum_generation]
% bPop   - a matrix of best solutions [generation_found solution_string]
% endPop - the current generation of solutions

%%  
currentGen = ops(1);
maxGen     = ops(2);
done       = currentGen >= maxGen; 

4.7 nonUnifMutation.m

function parent = nonUnifMutation(parent, bounds, Ops)

%%  非均匀突变基于非均匀概率分布改变父代的参数之一
% parent  - the first parent ( [solution string function value] )
% bounds  - the bounds matrix for the solution space
% Ops     - Options for nonUnifMutate[gen #NonUnifMutations maxGen b]

%%  相关参数设置
cg = Ops(1); 				              % 当前这一代
mg = Ops(3);                              % 最大代数
bm = Ops(4);                              % 形状参数
numVar = size(parent, 2) - 1; 	          % 获取变量个数
mPoint = round(rand * (numVar - 1)) + 1;  % 选择一个变量从 1 到变量数随机变化
md = round(rand); 			              % 选择突变方向
if md 					                  % 向上限突变
  newValue = parent(mPoint) + delta(cg, mg, bounds(mPoint, 2) - parent(mPoint), bm);
else 					                  % 向下限突变
  newValue = parent(mPoint) - delta(cg, mg, parent(mPoint) - bounds(mPoint, 1), bm);
end
parent(mPoint) = newValue; 		          % 产生子代

4.8 normGeomSelect.m

function newPop = normGeomSelect(oldPop, options)

% NormGeomSelect 是一个基于归一化几何分布的排序选择函数。

% newPop  - the new population selected from the oldPop
% oldPop  - the current population
% options - options to normGeomSelect [gen probability_of_selecting_best]

%%  交叉选择排序
q = options(2); 				    % 选择最佳的概率
e = size(oldPop, 2); 			    % xZome 的长度，即 numvars + fit
n = size(oldPop, 1);  		        % 种群数目
newPop = zeros(n, e); 		        % 为返回 pop 分配空间
fit = zeros(n, 1); 		            % 为选择概率分配空间
x = zeros(n,2); 			        % rank和id的排序列表
x(:, 1) = (n : -1 : 1)'; 	        % 要知道它是什么元素
[~, x(:, 2)] = sort(oldPop(:, e));  % 排序后获取索引

%%  相关参数
r = q / (1 - (1 - q) ^ n); 			            % 归一化分布，q 素数
fit(x(:, 2)) = r * (1 - q) .^ (x(:, 1) - 1); 	% 生成选择概率
fit = cumsum(fit); 			                    % 计算累积概率

%% 
rNums = sort(rand(n, 1)); 			            % 生成 n 个排序的随机数
fitIn = 1;                                      % 初始化循环控制
newIn = 1; 			                            % 初始化循环控制
while newIn <= n 				                % 获得 n 个新个体
  if(rNums(newIn) < fit(fitIn)) 		
    newPop(newIn, :) = oldPop(fitIn, :); 	    % 选择 fitIn 个人
    newIn = newIn + 1; 			                % 寻找下一个新人
  else
    fitIn = fitIn + 1; 			                % 着眼于下一个潜在选择
  end
end

4.9 parse.m

function x = parse(inStr)

% parse 是一个函数，它接收一个由空格分隔的文本组成的字符串向量，
% 并将各个字符串项解析为一个 n 项矩阵，每个字符串一行。

% x     - the return matrix of strings
% inStr - the blank separated string vector

%%  切割字符串
strLen = size(inStr, 2);
x = blanks(strLen);
wordCount = 1;
last = 0;
for i = 1 : strLen
  if inStr(i) == ' '
    wordCount = wordCount + 1;
    x(wordCount, :) = blanks(strLen);
    last = i;
  else
    x(wordCount, i - last) = inStr(i);
  end
end

4.10 gadecod.m

function [val, W1, B1, W2, B2] = gadecod(x)

%%  读取主空间变量
S1 = evalin('base', 'S1');             % 读取隐藏层神经元个数
net = evalin('base', 'net');           % 读取网络参数
p_train = evalin('base', 'p_train');   % 读取输入数据
t_train = evalin('base', 't_train');   % 读取输出数据

%%  参数初始化
R2 = size(p_train, 1);                 % 输入节点数 
S2 = size(t_train, 1);                 % 输出节点数

%%  输入权重编码
for i = 1 : S1
    for k = 1 : R2
        W1(i, k) = x(R2 * (i - 1) + k);
    end
end

%%  输出权重编码
for i = 1 : S2
    for k = 1 : S1
        W2(i, k) = x(S1 * (i - 1) + k + R2 * S1);
    end
end

%%  隐层偏置编码
for i = 1 : S1
    B1(i, 1) = x((R2 * S1 + S1 * S2) + i);
end

%%  输出偏置编码
for i = 1 : S2
    B2(i, 1) = x((R2 * S1 + S1 * S2 + S1) + i);
end

%%  赋值并计算
net.IW{1, 1} = W1;
net.LW{2, 1} = W2;
net.b{1}     = B1;
net.b{2}     = B2;

%%  模型训练
net.trainParam.showWindow = 0;      % 关闭训练窗口
net = train(net, p_train, t_train);

%%  仿真测试
t_sim1 = sim(net, p_train);

%%  计算适应度值
val =  1 ./ (sqrt(sum((t_sim1 - t_train).^2) ./ length(t_sim1)));

4.11 main.m

%%  清空环境变量
warning off             % 关闭报警信息
close all               % 关闭开启的图窗
clear                   % 清空变量
clc                     % 清空命令行

%%  导入数据（时间序列的单列数据）
result = xlsread('数据集.xlsx');

%%  添加路径
addpath('goat\')

%%  数据分析
num_samples = length(result);  % 样本个数 
kim = 15;                      % 延时步长（kim个历史数据作为自变量）
zim =  1;                      % 跨zim个时间点进行预测

%%  构造数据集
for i = 1: num_samples - kim - zim + 1
    res(i, :) = [reshape(result(i: i + kim - 1), 1, kim), result(i + kim + zim - 1)];
end

%%  划分训练集和测试集
temp = 1: 1: 922;

P_train = res(temp(1: 700), 1: 15)';
T_train = res(temp(1: 700), 16)';
M = size(P_train, 2);

P_test = res(temp(701: end), 1: 15)';
T_test = res(temp(701: end), 16)';
N = size(P_test, 2);

%%  数据归一化
[p_train, ps_input] = mapminmax(P_train, 0, 1);
p_test = mapminmax('apply', P_test, ps_input);

[t_train, ps_output] = mapminmax(T_train, 0, 1);
t_test = mapminmax('apply', T_test, ps_output);

%%  建立模型
S1 = 5;           %  隐藏层节点个数                
net = newff(p_train, t_train, S1);

%%  设置参数
net.trainParam.epochs = 1000;        % 最大迭代次数 
net.trainParam.goal   = 1e-6;        % 设置误差阈值
net.trainParam.lr     = 0.01;        % 学习率

%%  设置优化参数
gen = 50;                       % 遗传代数
pop_num = 5;                    % 种群规模
S = size(p_train, 1) * S1 + S1 * size(t_train, 1) + S1 + size(t_train, 1);
                                % 优化参数个数
bounds = ones(S, 1) * [-1, 1];  % 优化变量边界

%%  初始化种群
prec = [1e-6, 1];               % epslin 为1e-6, 实数编码
normGeomSelect = 0.09;          % 选择函数的参数
arithXover = 2;                 % 交叉函数的参数
nonUnifMutation = [2 gen 3];    % 变异函数的参数

initPpp = initializega(pop_num, bounds, 'gabpEval', [], prec);  

%%  优化算法
[Bestpop, endPop, bPop, trace] = ga(bounds, 'gabpEval', [], initPpp, [prec, 0], 'maxGenTerm', gen,...
                           'normGeomSelect', normGeomSelect, 'arithXover', arithXover, ...
                           'nonUnifMutation', nonUnifMutation);

%%  获取最优参数
[val, W1, B1, W2, B2] = gadecod(Bestpop);

%%  参数赋值
net.IW{1, 1} = W1;
net.LW{2, 1} = W2;
net.b{1}     = B1;
net.b{2}     = B2;

%%  模型训练
net.trainParam.showWindow = 1;       % 打开训练窗口
net = train(net, p_train, t_train);  % 训练模型

%%  仿真测试
t_sim1 = sim(net, p_train);
t_sim2 = sim(net, p_test );

%%  数据反归一化
T_sim1 = mapminmax('reverse', t_sim1, ps_output);
T_sim2 = mapminmax('reverse', t_sim2, ps_output);

%%  均方根误差
error1 = sqrt(sum((T_sim1 - T_train).^2) ./ M);
error2 = sqrt(sum((T_sim2 - T_test ).^2) ./ N);

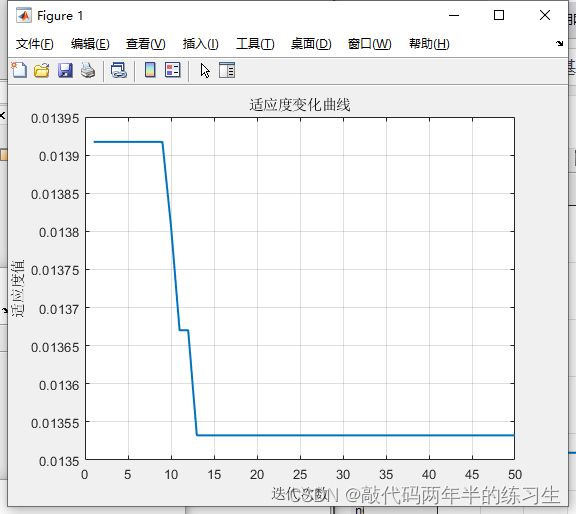
%%  优化迭代曲线
figure
plot(trace(:, 1), 1 ./ trace(:, 2), 'LineWidth', 1.5);
xlabel('迭代次数');
ylabel('适应度值');
string = {'适应度变化曲线'};
title(string)
grid on

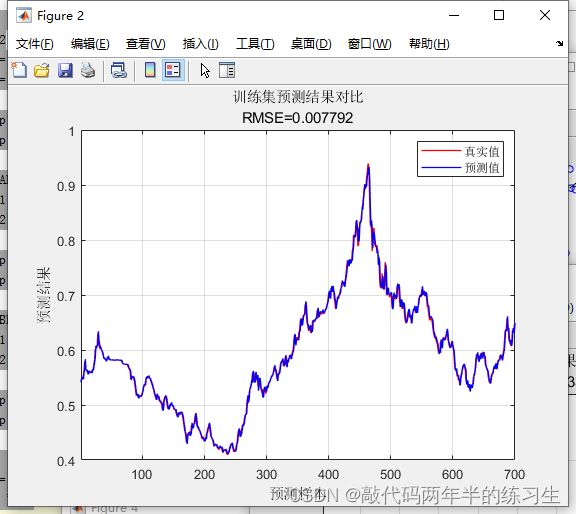
%%  绘图
figure
plot(1: M, T_train, 'r-', 1: M, T_sim1, 'b-', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'训练集预测结果对比'; ['RMSE=' num2str(error1)]};
title(string)
xlim([1, M])
grid

figure
plot(1: N, T_test, 'r-', 1: N, T_sim2, 'b-', 'LineWidth', 1)
legend('真实值', '预测值')
xlabel('预测样本')
ylabel('预测结果')
string = {'测试集预测结果对比'; ['RMSE=' num2str(error2)]};
title(string)
xlim([1, N])
grid

%%  相关指标计算
% R2
R1 = 1 - norm(T_train - T_sim1)^2 / norm(T_train - mean(T_train))^2;
R2 = 1 - norm(T_test -  T_sim2)^2 / norm(T_test -  mean(T_test ))^2;

disp(['训练集数据的R2为：', num2str(R1)])
disp(['测试集数据的R2为：', num2str(R2)])

% MAE
mae1 = sum(abs(T_sim1 - T_train)) ./ M ;
mae2 = sum(abs(T_sim2 - T_test )) ./ N ;

disp(['训练集数据的MAE为：', num2str(mae1)])
disp(['测试集数据的MAE为：', num2str(mae2)])

% MBE
mbe1 = sum(T_sim1 - T_train) ./ M ;
mbe2 = sum(T_sim2 - T_test ) ./ N ;

disp(['训练集数据的MBE为：', num2str(mbe1)])
disp(['测试集数据的MBE为：', num2str(mbe2)])

%%  绘制散点图
sz = 25;
c = 'b';

figure
scatter(T_train, T_sim1, sz, c)
hold on
plot(xlim, ylim, '--k')
xlabel('训练集真实值');
ylabel('训练集预测值');
xlim([min(T_train) max(T_train)])
ylim([min(T_sim1) max(T_sim1)])
title('训练集预测值 vs. 训练集真实值')

figure
scatter(T_test, T_sim2, sz, c)
hold on
plot(xlim, ylim, '--k')
xlabel('测试集真实值');
ylabel('测试集预测值');
xlim([min(T_test) max(T_test)])
ylim([min(T_sim2) max(T_sim2)])
title('测试集预测值 vs. 测试集真实值')

5.运行结果