最强大脑系列C++编程题，等你大展身手！

A00001. 指针排列

题目描述

小明买了一批淘宝的正宗小指针，共有m排n列，它们有着很神奇的特性，只能朝向八个方向，分别是东，南，西，北，东南，东北，西南，西北（D,N,X,B,DN,DB,XN,XB），如果你一次没有转到另一个方向，它就会返回到原来的状态，由于商家的不负责，指针的方向各不相同，于是小明想把指针转到一个方向，但他想知道自己最少需要花多少时间。于是，他拿放指针共需要0.5秒，并且把所有指针的方向和自己转指针的速度R告诉了你。快来帮他算算吧

输入格式

第一行是整数m,n，中间用空格隔开

第二行是整数R，表示每转R度需要一秒

第3行-第m+2行，每行有n个字符数据，中间用空格隔开（空格数量不一定）

输出格式

一行一个4位小数，表示需要的时间。（单位：秒）

5 5
90
D  D  D  D  D
D D D D D
B B B B B
DN  DN  DN  DN  DN  
D D D D D

12.5000

样例解释 1

买的指针有5行5排,每秒转90度

经过判断，应该转到D方向，所以转B方向的指针需要转90度，转DN方向指针需要转45度

十个指针共要转（90+45)×5=675度，需要675/90=7.5秒，拿放指针需要10×0.5=5秒，总共需要7.5+5=12.5秒

数据规模与约定

m<=5000;n<=5000
R<=2000（有的时候他会找许多好帮手）

---

A00002. 黑白迭代

题目描述

1.游戏规则

在m*n的空白盘面上，每点击一个方格，该方格和四周的方格会出现反色，你需要记忆目标图形，并将其在空白盘面上完美构建。

事实上，黑白迭代和一个经典的游戏—— 点灯游戏 （又名关灯/灭灯游戏或翻转游戏）非常类似，只需要把二者初始状态和目标状态对调即可（黑白迭代初始全白，目标指定图形；而点灯游戏则是初始指定图形，目标全点亮。）过程和规则是完全相同的。 点灯游戏规则： 在一个m×n的方格里，有若干盏灯亮着。点击任意一盏灯(不管此灯是亮着还是灭着，都可以点)，那么该灯以及与该灯相邻的上、下、左、右共五盏灯都同时会变成与自身相反的状态，即亮的变灭，灭的变亮。如何点亮所有的灯？

输入格式

第一行是m和n，中间用空格隔开

第2到n+1行，每行m个数据。表示目标图形

输出格式

一行一个坐标，即需要操作的方格。（从左往右，从上到下输出，尽量使操作方格最少）

5 5
0 0 0 0 0
0 0 1 0 0
0 1 1 1 0
0 0 1 0 0
0 0 0 0 0

3 3

数据规模与约定

对于 $100\%$ 的数据，$1\le n\le 2\times 10^3$，$1\le m\le 2\times 10^3$。。

A00003. 康斯推理

题目描述

1.游戏规则

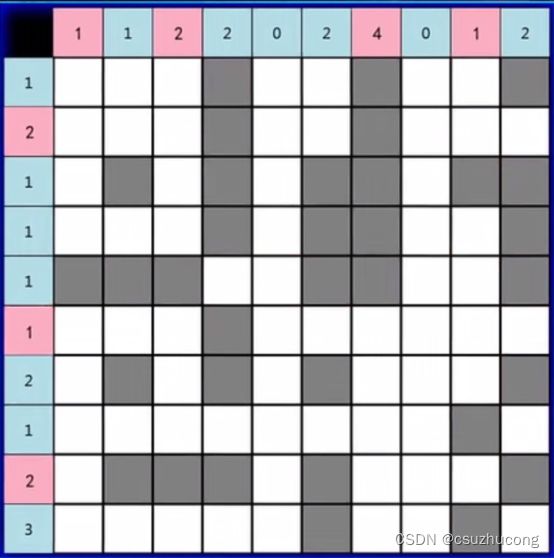
有一个m*n的盘面上，给出每行每列的目标数，黑格子不含目标，找出所有目标，输出所有的答案和总的答案数（先输出在左上有目标的答案）

输入格式

第1行是m和n，中间用空格隔开

第2行，m个数据。表示每列的目标图形

第3行，n个数据。表示每行的目标图形

输出格式

输出的第一行是总方案数s。

后面是s个方阵，X表示目标位置，0表示没有目标，中间用空格隔开

2 2
1 1
1 1
0 0 
0 0

2
X 0
0 X

0 X
X 0

输入数据 2

3 3
1 1 1
1 1 1
0 0 0
0 1 0
0 0 0

输出数据 2

4
X 0 0
0 0 X
0 X 0

0 X 0
X 0 0
0 0 X

0 X 0
0 0 X
X 0 0

0 0 X
X 0 0
0 X 0

数据规模与约定

对于 $100\%$ 的数据，$1\le n\le 2\times 10^3$，$1\le m\le 2\times 10^3$。。

---

A00004. 六宫数局

题目描述

1.游戏规则

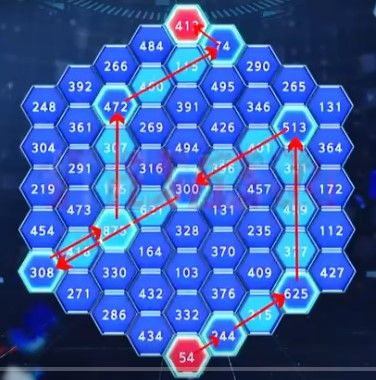
在边长为n的六边形盘面上，有很多数，你需要分析各个数的质因数，从最下面一个格子走到最上一个格子

输入格式

第一行是n，

第2到n行，每行m个数据。表示目标图形（翻转了90度）

输出格式

一行2个数，即移动到的方格。（使经过数字最少，如果相同则输出经过数字的和最少的）

5
        308 454 219 304 248
      271 416 473 291 361 392 
    286 330 875 175 367 472 266
  434 432 164 621 316 269 450 484
54 332 103 328 300 494 391 115 413
  244 376 370 131 356 426 495 74
    215 409 235 457 401 346 290
      625 317 459 321 513 265
        427 112 172 364 131

54->244
244->625
625->513
513->300
300->308
308->875
875->472
472->74
74->413

数据规模与约定

对于 $100\%$ 的数据，$1\le n\le 2\times 10^3$，

---

A00005 移星掠形

题目描述

1.游戏规则

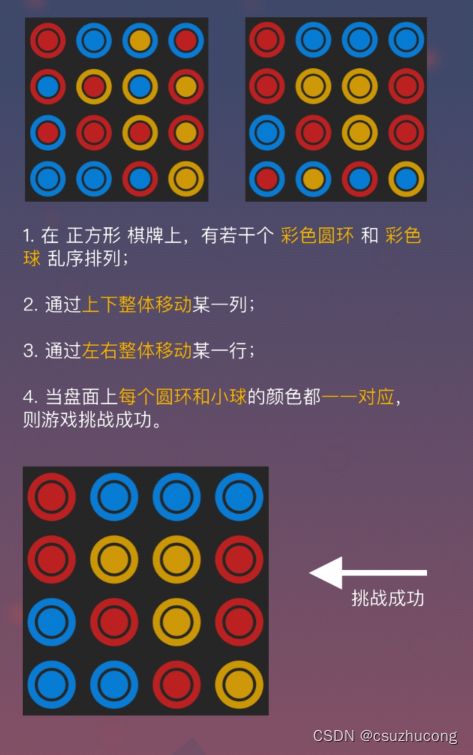
有一个m*n的盘面上，给出目标图形和现有图形，将现有图形变换成目标图形，移动时该行或该列所有图形全部移动一格，最后一个图形自动补在第一个

输入格式

第1行是m和n，中间用空格隔开

第2行到第n+1行，每行m个数据。表示每列的现有图形

第n+2行到第2n+1行，每行m个数据。表示每列的目标图形

输出格式

多行数，表示需要操作的行和列

(“<”表示把一行往左，“>”表示把一行向右，

“+”表示把一列向上，“-”表示把一列向下，

默认先操作行，后操作列，

操作行先操作上面，操作列先操作左边，

总的操作次数应当最少)

2 2
1 2
1 2
2 1
2 1

1>
2>

输入数据 2

3 3
0 0 0
0 0 0
0 1 1
1 1 0
0 0 0
0 0 0

输出数据 2

3<
1-
2-

数据规模与约定

对于 $100\%$ 的数据，$1\le n\le 2\times 10^3$，$1\le m\le 2\times 10^3$。。

---

#include 
using namespace std;
int main()
{
	cout<<"代码可以发评论区";
	return 0;
}