【数学建模】2018年数学建模国赛C题 问题一代码
文章目录
- 问题一代码
-
-
- 导入包及数据
- 数据探索与预处理
- 会员统计分析
-
- 分析会员的年龄构成、男女比例等基本信息
- 分析会员的总订单占比,总消费金额占比等消费情况
- 分别以季度和天为单位,分析不同时间段会员的消费时间偏好
- 会员与非会员统计分析
-
问题一代码
本文从购买力、购买时间偏好两个维度分析会员的消费特征。
以会员消费总金额、消费次数、商品购买数量代表会员购买力;
同时按季节和天对会员消费行为进行消费时间偏好分析。
同时对会员及非会员的消费次数和消费金额进行对比分析。
导入包及数据
import matplotlib
import warnings
import re
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.preprocessing import StandardScaler,MinMaxScaler
%matplotlib inline
plt.rcParams['font.sans-serif'] = 'SimHei'
plt.rcParams['axes.unicode_minus'] = False
matplotlib.rcParams.update({'font.size' : 16})
plt.style.use('ggplot')
warnings.filterwarnings('ignore')
data1=pd.read_excel('./2018-C-Chinese的副本/附件1-会员信息表.xlsx')
data2=pd.read_excel('./2018-C-Chinese的副本/附件3-会员消费明细表.xlsx')
数据探索与预处理
1.附件一会员信息表探索与预处理
#查看是否缺失数据
print('会员信息表一共有{}行记录,{}列'.format(data1.shape[0],data1.shape[1]))
print('数据缺失情况为:\n',data1.isnull().sum())
print('会员不重复卡号kh的信息有',len(data1['kh'].unique()))
#会员卡号去重
print("去除重复值前的数据量", data1.shape)
data1.drop_duplicates(subset=['kh'],keep='first',inplace=True)
print("去除重复值后的数据量", data1.shape)
#去除登记时间的缺失值,并去重
print("去除重复值前的数据量", data1.shape)
data1.dropna(subset='djsj',inplace=True)
print("去除登记时间的缺失值,并去重数据量", data1.shape)
#性别上缺失的比例较少,所以使用众数填充
data1['xb'].fillna(data1['xb'].mode().values[0],inplace=True)
#检验是否在登记时间这一字段中存在异常值,若存在异常值,则无法进行基本操作
data1_1 = data1['djsj'] + pd.Timedelta(days=1)
#查看处理完成的数据缺失值情况
data1.isnull().sum()
#对于出生日期的处理
#由于出生日期缺失值过多,且存在较多的异常值,不能贸然删除
#故下面另建一个数据集L来保存“出生日期”和‘性别’信息,方便下面对会员的性别和年龄信息进行统计
L = pd.DataFrame(data1.loc[data1['csny'].notnull(),['csny','xb']])
L['age'] = L['csny'].astype(str).apply(lambda x:x[0:3]+'0')
L.drop('csny',axis=1,inplace=True)
L['age'].value_counts()
# 出生日期这列中出现较多的异常值,以一个正常人寿命为100年算起,我们假定会员年龄范围在1922-2022年起
# 将超过该范围的值当作异常值进行剔除
L['age'] = L['age'].astype(int)
condaition = 'age >= 1922 and age <=2022'
L = L.query(condaition)
L.index = range(L.shape[0])
L['age'].value_counts()
# 用于与销售流水表进行合并的数据只取['会员卡号', '性别', '登记时间']这三列,将出生日期这列意义不大的进行删除(这列信息最有可能出错),并重置索引
data1.drop('csny', axis = 1, inplace = True)
data1.index = range(data1.shape[0])
print('数据清洗之后共有{}行记录,{}列字段,字段分别为{}'.format(data1.shape[0], data1.shape[1], data1.columns.tolist()))
2.附件三会员销售流水表
对于不是本地会员的会员当作非会员处理。
#检查是否含有缺失值
print('未处理时的数据数目:',data2.shape[0],data2.shape[1])
print('缺失值数据数目:',data2.isnull().sum())
#检查将售价、数量、金额、积分是否都大于0
print('商品售价大于0的数量:{} \t 全部记录有{}'.format(len(data2['sj']>0),len(data2['sj'])))
print('商品数量大于0的数量:{} \t 全部记录有{}'.format(len(data2['sl']>0),len(data2['sl'])))
print('会员积分大于0的数量:{} \t 全部记录有{}'.format(len(data2['jf']>0),len(data2['jf'])))
data2.drop(['syjh', 'gzbm', 'gzmc'], axis = 1, inplace = True)
# 重置索引
data2.index = range(data2.shape[0])
3.将会员信息表喝会员消费信息明细进行合并
#按照两表的卡号信息将两表合并,将附件2中有会员卡号的进行左合并,得到附件1会员和非会员的数据
data_merge = pd.merge(data2,data1,on='kh',how='left')
data_merge
# 再次查看金额>0,积分>0,数量>0
index1 = data_merge['je'] > 0
index2 = data_merge['jf'] > 0
index3 = data_merge['sl'] > 0
data_merge1 = data_merge.loc[index1 & index2 & index3,:]
data_merge1.index = range(data_merge1.shape[0])
data_merge1.shape
#创造字段检查其是否为会员
data_merge1['vip'] = 1
data_merge1
data_merge1.loc[data_merge1['xb'].isnull(),'vip'] = 0
data_merge1
4.处理附件二
data_total = pd.read_excel('./2018-C-Chinese的副本/附件2-销售流水表.xlsx')
print(data_total.shape)
print(data_total.isnull().sum()) #未发现缺失值
data_total = data_total.drop_duplicates()
print(data_total.shape)
#检查将售价、数量、金额、积分是否都大于0
print('商品售价大于0的数量:{} \t 全部记录有{}'.format(len(data_total['sj']>0),len(data_total['sj'])))
print('商品数量大于0的数量:{} \t 全部记录有{}'.format(len(data_total['sl']>0),len(data_total['sl'])))
print('积分大于0的数量:{} \t 全部记录有{}'.format(len(data_total['je']>0),len(data_total['je'])))
#检验是否在-登记时间这一字段中存在异常值,若存在异常值,则无法进行基本操作
data_total_1 = data_total['dtime'] + pd.Timedelta(days=1)
#经检验日期时间没有问题
5.附件二和上处理的一三合并的文件进行二次合并
#检查各个数据集长度
print(f'附件二{len(data_total)}\t附件一和三合并{len(data_merge1)}')
data23 = pd.merge(data_total,data_merge1,on=['dtime','spbm','je'],how='left')
data23.loc[data23['vip'].isnull(),'vip'] = 0
data23.drop(['kh','sj_y','sl_y','kh','xb','djsj'],axis=1,inplace=True)
fig, axs = plt.subplots(1, 2, figsize = (12, 7), dpi = 100)
axs[0].pie([len(data23.loc[data23['vip']==1,'dtime'].unique()),len(data23.loc[data23['vip']==0,'dtime'].unique())],
labels = ['vip','normal'], wedgeprops = {'width': 0.4}, counterclock = False, autopct = '%.2f%%', pctdistance = 0.8)
axs[0].set_title('total dingdan%')
axs[1].pie([data23.loc[data23['vip'] == 1, 'je'].sum(), data23.loc[data23['vip'] == 0, 'je'].sum()],
labels = ['vip', 'normal'], wedgeprops = {'width': 0.4}, counterclock = False, autopct = '%.2f%%', pctdistance = 0.8)
axs[1].set_title('total je%')
会员统计分析
分析会员的年龄构成、男女比例等基本信息
#处理男女比例这一列,女0,男1
L['xb'] = L['xb'].apply(lambda x:'male' if x==1 else 'female')
sex_sort = L['xb'].value_counts()
#将年龄划分为不同年龄段
#老年(1920-1950)、中年(1960-1990)、青年(1990-2010)
L['age group']='middle'
L.loc[L['age'] <= 1950,'age group'] = 'old'
L.loc[L['age'] >= 1990,'age group'] = 'young'
res = L['age group'].value_counts()
#使用上述预处理后的数据L,包含两个字段,分别是age和性别,先画出年龄条形图
fig, axs = plt.subplots(1,2,figsize=(16,7),dpi=100)
#绘制条形图
ax = sns.countplot(x='age',data = L,ax = axs[0])
for p in ax.patches:
height = p.get_height()
ax.text(x = p.get_x() + (p.get_width() / 2), y = height + 500, s = '{:.0f}'.format(height), ha = 'center')
axs[0].set_title('year of birth')
# 绘制饼图
axs[1].pie(sex_sort, labels = sex_sort.index, wedgeprops = {'width': 0.4}, counterclock = False, autopct = '%.2f%%', pctdistance = 0.8)
axs[1].set_title('male vs female')
# 绘制各个年龄段的饼图
plt.figure(figsize = (8, 6), dpi = 100)
plt.pie(res.values, labels = ['middle', 'young', 'old'], autopct = '%.2f%%', pctdistance = 0.8,
counterclock = False, wedgeprops = {'width': 0.4})
plt.title('fenbu')
#plt.savefig('./age fenbu.png')
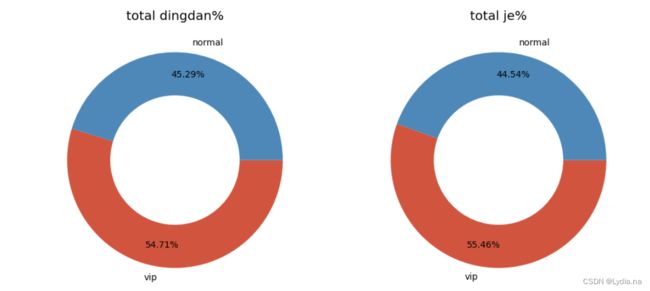
分析会员的总订单占比,总消费金额占比等消费情况
fig, axs = plt.subplots(1, 2, figsize = (12, 7), dpi = 100)
axs[0].pie([len(data_merge1.loc[data_merge1['vip']==1,'dtime'].unique()),len(data_merge1.loc[data_merge1['vip']==0,'dtime'].unique())],
labels = ['vip','normal'], wedgeprops = {'width': 0.4}, counterclock = False, autopct = '%.2f%%', pctdistance = 0.8)
axs[0].set_title('total dingdan%')
axs[1].pie([data_merge1.loc[data_merge1['vip'] == 1, 'je'].sum(), data_merge1.loc[data_merge1['vip'] == 0, 'je'].sum()],
labels = ['vip', 'normal'], wedgeprops = {'width': 0.4}, counterclock = False, autopct = '%.2f%%', pctdistance = 0.8)
axs[1].set_title('total je%')
分别以季度和天为单位,分析不同时间段会员的消费时间偏好
不同季度和天为单位的消费时间偏好
# 将会员的消费数据另存为另一个数据集
df_vip = df1.dropna()
df_vip.drop(['会员'], axis = 1, inplace = True)
df_vip.index = range(df_vip.shape[0])
df_vip.info()
# 将“消费产生的时间”转变成日期格式
df_vip['消费产生的时间'] = pd.to_datetime(df_vip['消费产生的时间'])
# 新增四列数据,季度、天、年份和月份的字段
df_vip['年份'] = df_vip['消费产生的时间'].dt.year
df_vip['月份'] = df_vip['消费产生的时间'].dt.month
df_vip['季度'] = df_vip['消费产生的时间'].dt.quarter
df_vip['天'] = df_vip['消费产生的时间'].dt.day
df_vip.head()
# 前提假设:2015-2018年之间,消费者偏好在时间上不会发生太大的变化(均值),消费偏好——>以不同时间的订单数来衡量
quarters_list, quarters_order = orders(df_vip, '季度', 3)
days_list, days_order = orders(df_vip, '天', 36)
time_list = [quarters_list, days_list]
order_list = [quarters_order, days_order]
maxindex_list = [quarters_order.index(max(quarters_order)), days_order.index(max(days_order))]
fig, axs = plt.subplots(1, 2, figsize = (18, 7), dpi = 100)
colors = np.random.choice(['r', 'g', 'b', 'orange', 'y'], replace = False, size = len(axs))
titles = ['季度的均值消费偏好', '天数的均值消费偏好']
labels = ['季度', '天数']
for i in range(len(axs)):
ax = axs[i]
ax.plot(time_list[i], order_list[i], linestyle = '-.', c = colors[i], marker = 'o', alpha = 0.85)
ax.axvline(x = time_list[i][maxindex_list[i]], linestyle = '--', c = 'k', alpha = 0.8)
ax.set_title(titles[i])
ax.set_xlabel(labels[i])
ax.set_ylabel('均值消费订单数')
print(f'{titles[i]}最优的时间为: {time_list[i][maxindex_list[i]]}\t 对应的均值消费订单数为: {order_list[i][maxindex_list[i]]}')
plt.savefig('./季度和天数的均值消费偏好情况.png')
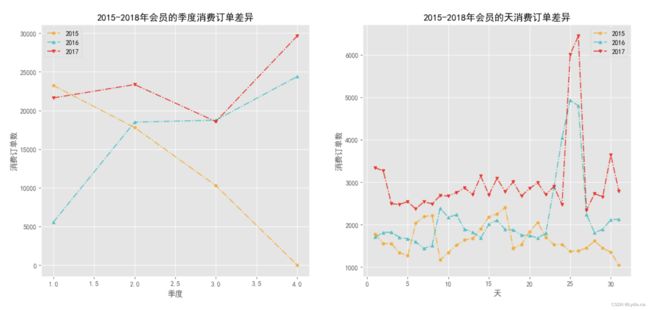
# 自定义函数来绘制不同年份之间的的季度或天数的消费订单差异
def plot_qd(df, label_y, label_m, nrow, ncol):
"""
df: 为DataFrame的数据集
label_y: 为年份的字段标签
label_m: 为标签的一个列表
n_row: 图的行数
n_col: 图的列数
"""
# 必须去掉最后一年的数据,只能对2015-2017之间的数据进行分析
y_list = np.sort(df[label_y].unique().tolist())[:-1]
colors = np.random.choice(['r', 'g', 'b', 'orange', 'y', 'k', 'c', 'm'], replace = False, size = len(y_list))
markers = ['o', '^', 'v']
plt.figure(figsize = (8, 6), dpi = 100)
fig, axs = plt.subplots(nrow, ncol, figsize = (16, 7), dpi = 100)
for k in range(len(label_m)):
m_list = np.sort(df[label_m[k]].unique().tolist())
for i in range(len(y_list)):
order_m = []
index1 = df[label_y] == y_list[i]
for j in range(len(m_list)):
index2 = df[label_m[k]] == m_list[j]
order_m.append(len(df.loc[index1 & index2, '消费产生的时间'].unique()))
axs[k].plot(m_list, order_m, linestyle ='-.', c = colors[i], alpha = 0.8, marker = markers[i], label = y_list[i], markersize = 4)
axs[k].set_xlabel(f'{label_m[k]}')
axs[k].set_ylabel('消费订单数')
axs[k].set_title(f'2015-2018年会员的{label_m[k]}消费订单差异')
axs[k].legend()
plt.savefig(f'./2015-2018年会员的{"和".join(label_m)}消费订单差异.png')
plot_qd(df_vip, '年份', ['季度', '天'], 1, 2)
# 自定义函数来绘制不同年份之间的月份消费订单差异
def plot_ym(df, label_y, label_m):
"""
df: 为DataFrame的数据集
label_y: 为年份的字段标签
label_m: 为月份的字段标签
"""
# 必须去掉最后一年的数据,只能对2015-2017之间的数据进行分析
y_list = np.sort(df[label_y].unique().tolist())[:-1]
m_list = np.sort(df[label_m].unique().tolist())
colors = np.random.choice(['r', 'g', 'b', 'orange', 'y'], replace = False, size = len(y_list))
markers = ['o', '^', 'v']
fig, axs = plt.subplots(1, 2, figsize = (18, 8), dpi = 100)
for i in range(len(y_list)):
order_m = []
money_m = []
index1 = df[label_y] == y_list[i]
for j in range(len(m_list)):
index2 = df[label_m] == m_list[j]
order_m.append(len(df.loc[index1 & index2, '消费产生的时间'].unique()))
money_m.append(df.loc[index1 & index2, '消费金额'].sum())
axs[0].plot(m_list, order_m, linestyle ='-.', c = colors[i], alpha = 0.8, marker = markers[i], label = y_list[i])
axs[1].plot(m_list, money_m, linestyle ='-.', c = colors[i], alpha = 0.8, marker = markers[i], label = y_list[i])
axs[0].set_xlabel('月份')
axs[0].set_ylabel('消费订单数')
axs[0].set_title('2015-2018年会员的消费订单差异')
axs[1].set_xlabel('月份')
axs[1].set_ylabel('消费金额总数')
axs[1].set_title('2015-2018年会员的消费金额差异')
axs[0].legend()
axs[1].legend()
plt.savefig('./2015-2018年会员的消费订单和金额差异.png')
# 调用函数
plot_ym(df_vip, '年份', '月份')
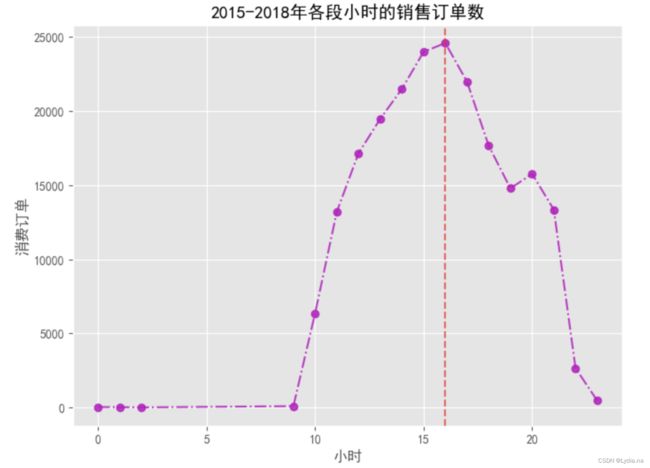
# 再来分析下时间上的差差异——消费订单数
df_vip['时间'] = df_vip['消费产生的时间'].dt.hour
x_list, order_nums = orders(df_vip, '时间', 1)
maxindex = order_nums.index(max(order_nums))
plt.figure(figsize = (8, 6), dpi = 100)
plt.plot(x_list, order_nums, linestyle = '-.', marker = 'o', c = 'm', alpha = 0.8)
plt.xlabel('小时')
plt.ylabel('消费订单')
plt.axvline(x = x_list[maxindex], linestyle = '--', c = 'r', alpha = 0.6)
plt.title('2015-2018年各段小时的销售订单数')
plt.savefig('./2015-2018年各段小时的销售订单数.png')
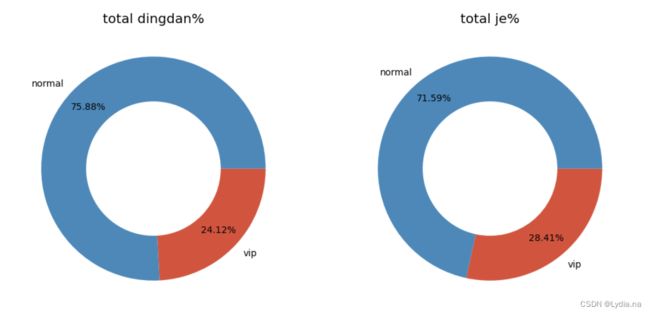
会员与非会员统计分析
fig, axs = plt.subplots(1, 2, figsize = (12, 7), dpi = 100)
axs[0].pie([len(data23.loc[data23['vip']==1,'dtime'].unique()),len(data23.loc[data23['vip']==0,'dtime'].unique())],
labels = ['vip','normal'], wedgeprops = {'width': 0.4}, counterclock = False, autopct = '%.2f%%', pctdistance = 0.8)
axs[0].set_title('total dingdan%')
axs[1].pie([data23.loc[data23['vip'] == 1, 'je'].sum(), data23.loc[data23['vip'] == 0, 'je'].sum()],
labels = ['vip', 'normal'], wedgeprops = {'width': 0.4}, counterclock = False, autopct = '%.2f%%', pctdistance = 0.8)
axs[1].set_title('total je%')