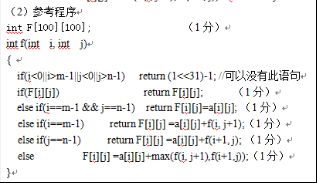算法设计与分析 期末考试试卷
1.渐进表示法中f(n)= O(g(n))意味着f(n)的数量级 [ 不大于 ] g(n)的数量级【填“小于”、“大于”、“不小于”或“不大于”】,平时各种教材中见到的O(n2)表达的意思是算法的复杂度
[ 等于 ] n2数量级【填“小于”、“等于”或“大于”】。
2.算法的正确性通常采用 【 理论证明 】 或测试的方法。
3.如果某算法的时间复杂度为θ(2n),机器的运算速度按109次/秒估算,则n= 【30 】时,机器运算时间为1秒钟【注:210≈1000】,如果n增大3,则运算时间会变为 【 8】 秒。
4.分治算法一般采用 【 二分法 】 。【填“二分法”、“三分法”或“n分法”】
5.用f(n,m)表示两个长度分别为n,m的字符串X、Y的最长公共子序列的长度,补充完整的递推式。
0 【 n== 0||m==0 】
f(n,m)={ f(n-1,m-1)+1 Xn=Ym
【Max(f(n-1,m),f(n,m-1) 】 Xn != Ym
6.对于运算量很大的问题,用随机方法其结果通常 【 】误差【填“有”或“没有”】
B.
C.
D.以上都不对
时间复杂度知识点梳理
2.按数量级排序,正确的是( B )。
A.n1/2 < (logn)2
B.n1/2 > (logn)2
C.logn> n
D.logn >n1/2

https://blog.csdn.net/qq_40811682/article/details/100052294
3.对数组元素a[from]~a[to]进行快速排序时,假设一趟相遇过程将元素a[from]移到数组单元a[pos],则初始元素a[from]在该区间是第(C)小元素。
A.to-from+1 B.from-pos+1 C. pos-from+1 D. to–pos+1
快速排序
4.对解空间树进行深度优先搜索的是( A )。
A.回溯算法 B.分支限界算法 C.分治算法
D.动态规划算法
5.硬币找零问题即是对于面值系统为a1,a2,…,ak(其中a1=1)且个数不限的k种硬币,找零S元钱,求最少硬币个数,关于这个问题的描述正确的是(D )。
A.对于任意面值系统贪心算法均可得到最优解
B.面值系统必须递减排序,动态规划算法才能得到最优解
C.贪心算法的时间复杂度是θ(kS)
D.动态规划算法的时间复杂度是θ(kS)
6.鬼牌除外的一副扑克牌,共有13种扑克牌,每种牌4张,不考虑花色,从中任取k张牌有多少种可能结果?该问题最适合的算法是( C )。
A.回溯算法
B.概率算法
C.动态规划算法
D.分治算法
7.如果一个问题采用贪心算法、动态规划算法、回溯算法、分支限界算法都可以得到最优解,对四种算法进行比较,你认为最有可能的是( B )。
A.动态规划算法效率最高
B.贪心算法效率最高
C.回溯算法效率最高
D.分支限界算法效率最高8.下面关于回溯算法与分支限界算法的描述,正确的是( A )。
A.前者不创建解空间树,后者创建解空间树
B.后者不创建解空间树,前者创建解空间树
C.两者均创建解空间树
D.两者均不创建解空间树
9.下面关于图论中弗洛伊德算法的描述,错误的是(C )。
A.能求图中任意两点的最小距离 B.算法可以用二维数组存放结果
C.算法适合有向图,不能用于无向图 D.图中边的权值必须是非负数
10.关于P类和NP类问题,下列说法正确的是( A )。
A.P类是容易处理的
B.NP类问题是不能处理的
C.P类=NP类
D.P类≠NP类
1.分析下面程序段的时间复杂度。
int i,j,s;
for(i=1;i<=n;i++)
for(s=0,j=1;s<=n;j++)
s=s+j;
O(N^1.5)
2.分析下面程序段的时间复杂度。
int x=n, i=1;
while(x>0)
{ x= x-i;
i=i*2;
}
Log(n+1)=O(logn)
3.请描述下面递归函数运行时可能发生的问题。
void f(int n)
{ int a[1000];
if(n>0) f(n-1);
}
int main() { int n=10000; f(n); return 0; }
栈内存不够,强制停止递归函数因为栈溢出而被操作系统强制结束
4.如果机器速度按109次/秒估算,那么下面程序所用时间大约是多少秒?
void f(int n)
{
if(n<0) return ;
else for(i=1;i<5;i++) f(n-1);
}
int main() { int n=20; f(n); return 0; }
【注:可以按210≈1000来估算。】
420=240=1000^4,
10004/109=10^3
斐波那契数的时间复杂度斐波那契数的时间复杂度、空间复杂度详解
四.解答题。(本大题3小题,每小题8分,共24分)
1.如果系统rand( )函数产生的随机数范围在[0,32767],请写出表达式产生[a,b]范围随机整数【其中a,b均为整数,且b-a<32767】,请写出表达式产生[0,1]范围且小数点后含有3位的随机小数。
rand()%(b-a+1)+a
Rand()*1001/1000

2.假设打印时间分别为6,3,8,1,4分钟的5个人同时排队等待一台打印机服务,一个人的等待时间=排在他前面的人的打印时间之和+自己的打印时间,为了求出使得所有人的等待时间总和最小的打印顺序,请给出一种贪心策略,并计算出所有人的等待时间之和。
贪心策略是时间短的先打印,等待时间之和15+34+43+62+8*1=49
3.分析下面算法程序的输出结果。
int n=3,X[100];
int xianjie(int k, int i)
{ if(k==1 && i<=2) return 0;
if(k==2 && i<=1) return 0;
return 1;
}
void f(int k)
{ if(k-1==n) { cout<<endl; for(int i=1;i<=n;i++) cout<<X[i]<<” ”; }
else for(int i=1;i<=n;i++)
if(xianjie(k,i))
{ X[k]=i; f(k+1);}
}
int main( ){ f(1); return 0;}
五.算法设计题。(本大题2小题,第1小题12分,第2小题14分,共26分)
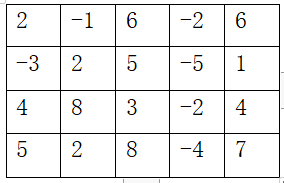
1.如图m*n方格矩阵a[m][n]中摆放着价值不等的宝贝(价值可正可负),从左上角a[0][0]出发到达右下角a[m-1][n-1],可以向右或向下走到相邻格子,并捡起当前格子的宝贝(无论价值的正负),每个格子只能走一遍,求能捡到宝贝价值之和的最大值。
(1)按动态规划算法的解题过程,写出递推关系式。(6分)
(2)根据递推关系式,写出递归型的动态规划函数。(6分)
2.n个正整数元素的集合a[],求元素之和为S的所有子集【注:集合元素依次为a[0],a[1],… a[n-1],要求有剪枝函数】。
#includeint X[100];
int sumS=0,leftS=35;
int xianzhi(int k,int i){
if(i==1&&sumS+a[k]>S) return 0;
if(i==0&&sumS+leftS-a[k]<S) return 0;
return 1;
}
void f(int k){
if(k-1==n){
if(sumS==S){
cout<<endl<<"{";
for(int i=0;i<=6;i++){
if(X[i]==1) cout<<a[i]<<", ";
}
cout<<"}";
}
}
else for(int i=0;i<=1;i++){
if(xianzhi(k,i)){
X[k]=i;
if(i==1){sumS+=a[k];leftS-=a[k];}
f(k+1);
if(i==1){sumS-=a[k];leftS+=a[k];}
}
}
}
int main(){
f(0);
return 0;
}