leetcode刷题189. 轮转数组(Java带注释)额外数组+环状替换+数组翻转
leetcode刷题189. 轮转数组
- 1. 题目描述
- 2.解法
-
- 2.1 使用额外的数组
- 2.2 环状替换(未完成)
- 2.3 数组翻转
1. 题目描述
给你一个数组,将数组中的元素向右轮转 k 个位置,其中 k 是非负数。
示例 1:
输入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]
解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
示例 2:
输入: nums = [-1,-100,3,99], k = 2
输出:[3,99,-1,-100]
解释:
向右轮转 1 步: [99,-1,-100,3]
向右轮转 2 步: [3,99,-1,-100]
提示:
- 1 <= nums.length <= 105
- -231 <= nums[i] <= 231 - 1
- 0 <= k <= 105
2.解法
2.1 使用额外的数组
这道题最先想到的应该就是这个,这个方法唯一需要算的是新的位置和旧的位置的关系,可以画图。
公式就是(i+k)%n
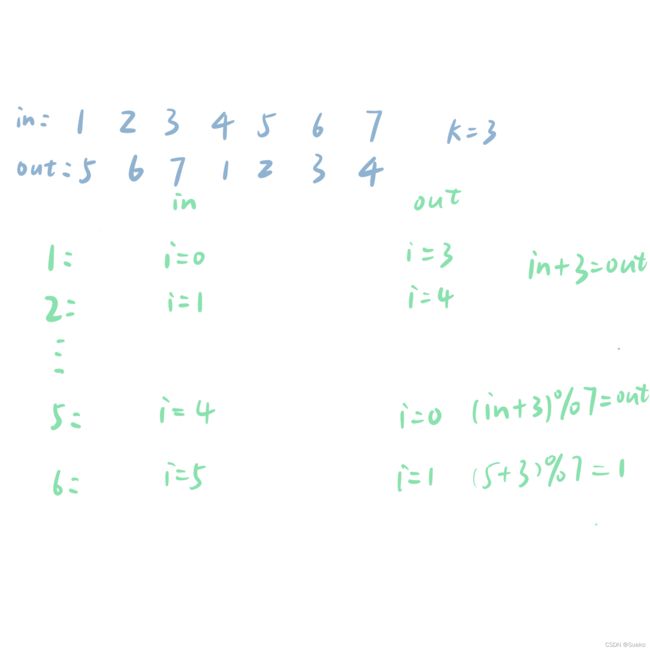
代码如下:
class Solution {
public void rotate(int[] nums, int k) {
int n = nums.length;
int []ans = new int[n];//新建数组
for(int i=0;i<n;i++){
ans[(i+k)%n] = nums[i];//将数组元素填入新的位置
}
System.arraycopy(ans, 0, nums, 0, n);//将新建数组拷贝进旧数组
}
}
2.2 环状替换(未完成)
第一种很明显浪费了很多空间。
而通过计算我们知道,可以两个元素之间进行位置的交换。
但是过程中如果不暂时保存一个元素的数据,将会被交换来的元素覆盖掉。
所以方法2就使用了一个temp来存储交换过程中先被覆盖的元素的值。
公式太复杂了,等我先把另外一题写完。(明天写)
2.3 数组翻转
数组反转也很好理解
比如[1,2,3,4,5,6] ,k=2
先将整个反转之后,[6,5,4,3,2,1]
再分别将[6,5]和[4,3,2,1]反转
就可以得到[5,6,1,2,3,4]。
主要就是写翻转函数,翻转函数只需要将头和尾交换就行。
class Solution {
public void rotate(int[] nums, int k) {
int n = nums.length;
k = k%n;
reverse(nums,0,n-1);//翻转整段
reverse(nums,0,k-1);//翻转前半部分
reverse(nums,k,n-1);//翻转后半部分
}
private void reverse(int []nums,int start,int end){//原地翻转数组
while(start<end){
int temp = nums[start];
nums[start] = nums[end];
nums[end] = temp;
start++;
end--;
}
}
}