数据结构代码总结(C语言实现)
目录
- 如何应对数据结构的代码题?
- 采取的学习流程
-
- ①首先对C语言的语法的熟悉
- ②学习掌握基本代码的写法,做到熟练
-
- 2.1插入排序
- 2.2快速排序
- 2.3二分查找
- 2.4树的遍历
- ③跟着网上视频开始熟悉对一些问题的解答
- ④结合真题的代码,寻找其中的结题规律
如何应对数据结构的代码题?
一开始我对代码题还是无从下手的,通过这些流程,对408真题上的代码逐渐理解并能自己写出个大概。希望我的复习流程可以大家提供一定的参考意义。
采取的学习流程
首先要明白几点,真题的代码是在一些基础代码的基础上进行增加参数,或者增加步骤,进而得到的
①首先对C语言的语法的熟悉
包括对结构体的定义,指针、数组、重命名,以及一些打印输出的句子。
学习的资料网址:菜鸟教程
基础的一些语法格式
定义结构体、以及重命名
typedef struct node{
int data;
struct node next;
}Lnode ,*List;
//这里利用typdef对结构体数据类型进行重命名,方便后面定义变量
//结构体变量struct node,命名为了Lnode,结构体变量struct node的指针命名为了,List
那么你可以用分别用:Lnode代替struct node ;List 代替struct node* 进行变量的定义
数组
int nums[5]={1,2,3,4,5};
nums=(int *)malloc(sizeof(int)*(n+1));
打印
char *a="123asd"
printf("(");
printf("%c",s);
②学习掌握基本代码的写法,做到熟练
基础代码
2.1插入排序
链表实现
注意插入排序链表实现的特点
维护的几个变量
LastSorted:已经排好序的最后一个结点
curr:需要进行插入排序的当前结点
Pre:寻找第一个大于当前结点之前的结点
//将结点指针变量的声明符号重新定义为 list 方便后续定义结点指针变量
typedef struct ListNode* list;
struct ListNode *insertionSortList(struct ListNode *head) {
if (head == NULL) {
return head;
}
list dummyHead = malloc(sizeof(struct ListNode));//虚拟头结点为了更好的对第一个元素之前进行插入
dummyHead->val = 0;
dummyHead->next = head;
list lastSorted = head;//已排序元素的最后一个元素
list curr = head->next;//当前需要进行判断的元素
while (curr != NULL) {
//当,当前元素大于等于已排好的最后元素,直接改最后元素
if(lastSorted->val<=curr->val)
{
lastSorted=lastSorted->next;
}
//当,当前元素小于已经排好元素时,需要从头开始找到第一个大于当前元素的前一个结点
else
{
list pre=dummyHead;
while(pre->next&&pre->next->val<=curr->val)//当下一个结点大于时,或者当前结点为最后一个结点时,跳出循环
{
pre=pre->next;
}
lastSorted->next=curr->next;//最后结点不变,最后结点的下一个结点变为原节点的下一节点
curr->next=pre->next;//当前结点的下一节点先修改
pre->next=curr;//然后修改pre结点的下一节点为当前结点
}
curr=lastSorted->next;//将已排序的后一个元素进行排序
}
return dummyHead->next;//最后返回head结点
}
数组实现
int insersorted(int a[],int n)
{
for(int i=2;i<n;i++)//从第二个元素开始
{
if(a[i]<a[i-1])//小于往前插入
{
a[0]=a[i];
for(int j=i-1;a[j]>a[0];j--)
{
a[j+1]=a[j];
}
a[j+1]=a[0]
}
}
2.2快速排序
//设计两个函数
//第一个函数实现每趟的交换排序
int partition(int *nums,int low,int high)
{
int tem=nums[low];
while(low<high)
{
while(low<high&&nums[high]>=tem)high--;
nums[low]=num[high];
while(low<high&&nums[low]<=tem)low++;
nums[high]=nums[low];
}
nums[low]=tem;
return low;//最后返回元素被最终放置的位置,然后以此为基点,对左右两边的数进行划分
}
//第二个函数实现递归的调用
int * quicksort(int * nums,int low,int high)
{
if(low<high)
{
int piv=partition(nums,low,high);
quicksort(nums,piv+1,high);
quicksort(nums,low,piv-1);
}
}
2.3二分查找
维护的变量
low:最左边的位置
high:最右边的位置
middle:中间的位置
每次根据中间位置值与目标变量的大小关系调整low和high的值
int searchInsert(int* nums, int numsSize, int target){
int low=0,high=numsSize-1,middle;
while(low<=high)
{
middle=(low+high)/2;
if(nums[middle]==target)
return middle;
else if(nums[middle]<target)
{
low=middle+1;
}
else
{
high=middle-1;
}
}
if (nums[middle]>target)
return middle;
else
return middle+1;
}
2.4树的遍历
递归实现
//先序遍历
typedef struct BiNode
{
struct BiNode* lchild,rchild;
int data;
}BNode,*BiTree;
void preorder(BiTree T)
{
if(T!=NUll)
{
visit(T);
preorder(T->lchild);
preorder(T->rchild);
}
}
//中序遍历
void inorder(Bitree T)
{
if(T!=NUll)
{
inorder(T->lchild);
visit(T);
inorder(T->rchild);
}
}
//后续遍历
void postorder(Bitree T)
{
if(T!=NUll)
{
postorder(T->lchild);
postorder(T->rchild);
visit(T);
}
}
非递归实现
//中序遍历
void inorder(BiTree T)
{
InitStack(S);//用于存储有左子树的根节点
BiTree p=T;//用于向下探索结点
while(P||isempty(S))//当T不为空,同时栈内存在元素时,循环
{
//如果当前结点不为空,则把器左节点放入栈中
if(p){
push(S,p);
p=p->lchild;
}
else
{
pop(S,p);
visit(p);
p=p->rchild;
}
}
}
③跟着网上视频开始熟悉对一些问题的解答
B站一位up主的的讲解视频:23考研数据结构编程代码题逐句精讲
看完视频并写完代码后,对于线性表的相关问题会有比较好的理解。
看视频时注重积累相关问题的结题方法,需要设置几个参数。
涉及的题目的结题代码
④结合真题的代码,寻找其中的结题规律
2009年

寻找倒数第k个结点,利用两个指针p,q, q先向后探测到第k-1个结点,如果此节点不是最后一个结点,那么p,q共同向后移动,知道q为最后一个结点,此时的p即为所求、
int find_k(Lnode *head, int k){
Lnode *p=head,*q=head;
int count=k-1;
while(count<k-1&&q->next){
q=q->next;
}
if(q->next==null) return 0;
while(q->next){
p=p->next;
q=q->next;
}
printf("倒数第%d个位置上的值为%d",k,p->data);
return 1;
}
2010年

将数组元素玄幻啊左移p位,那么可以采用对前p位反转,后n-p为反转,然后整体反转
void reverse(int *num,int low, int high)
{
int mark=(low+high)/2,tem;
for(int i=0;i<=mark;i++){
tem=num[i];
num[i]=num[low+high-i];
num[low+high-i]=tem;
}
}
void leftmove(int *num,int p,int n){
reverse(num,0,p-1);
reverse(num,p,n-1);
reverse(num,0,n-1);
}
2011年

因为s1、s2等长为L,那么中位数为第L个元素,因为s1、s2均为升序排序,所以我可以用p、q表示s1、s2的下标,每次比较s1[p],s2[q]的大小,更小的元素指针后移,同时记录下次数更小的那个数,当后移了L次时,即找到了答案。
时间复杂度为O(n),空间复杂度为O(1)
int find_middle(int* s1,int* s2,int L){
int count=0,p=0,q=0,pre_min;
whiel(count<L){
if(s1[p]<s2[q]){
pre_min=s1[p];
p++;
}
else{
pre_min=s2[q];
q++;
}
count++;
return pre_min;
}
2012年
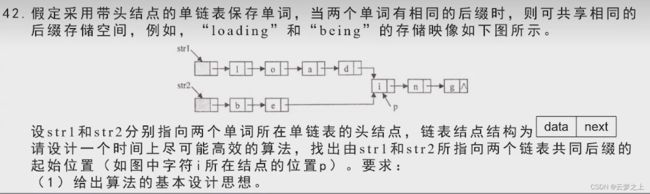
思路:
后缀的起始位置的点的特点,结点的地址的指针相同。(注意不是结点的值相同,虽然这里结点的值页相同但是,只考虑地址相同会更方便)
我们可以从后往前看,只要我们同时从后面往前数第一个重合的元素开始比较,然后第一个相同的就是我们要找的。
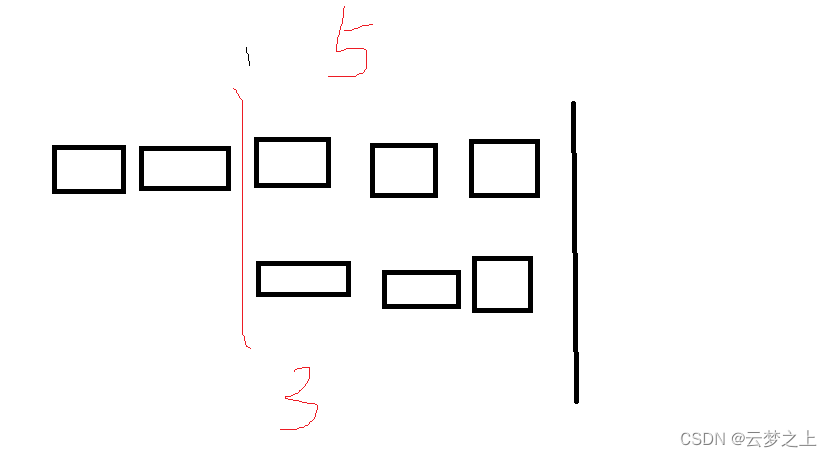
所以,可以先分别算出str1、str2的长度
然后算出长度的差值:distance
用pq分别记录各链表的点的指针
对于长的链表,p先后移distance个结点,然后pq开始比较
Lnode* find(Lnode* str1,Lnode* str2)
{
int m=0,n=0;
Lnode* tem=str1->next;
//先计算长度m、n
while(tem){
m++;
tem=tem->next;
}
tem=str2->next;
while(tem){
n++;
tem=tem->next;
}
Lnode *p=str1->next;
Lnode *q=str2->next;
//将链表队尾对齐
while(m>n){
p=p->next;
m--;
}
while(n>m){
q=q->next;
n--;
}
int flag=1;
//寻找第一个相同地址的结点,结束条件可能是找到最后没有找到那么就是null
while(flag&&p&&q){
if(p=q)flag=0;
else{
p=p-next;
q=q-next;
}
return p;
}
2014年

基础代码:先序遍历的递归实现
积累点
涉及对于需要考虑层数的,添加变量deep。
//在先序遍历的递归的基础上,加上参数deep(深度),然后在找到叶子节点时,计算权重:weight*deep,每次进行累加
typedef struct node{
struct node * left,*right;
int weight;
}*Btree;
static int count=0;//用来记录权重
void func1(Btree root,int deep)
{
if(root->left=NULL&&root->right=NULL)
{
count=count+(root->weight)*deep;//找到叶子节点时,计算权重
}
if(root->left)func1(root->left,deep+1);//未找到叶子结点,继续往下找,深度+1
if(root->right)func1(root->right,deep+1);
}
func1(root,0)//一开始我根节点,属于第0层
return count;
2015

思路
首先,目标是删除绝对值相同的结点,然后这里只考虑时间复杂度尽可能高效,所以,我们用空间换时间,采取数组,存放对于以访问数的情况。
数组下标为数的绝对值,0表示未被访问到,1表示已存在。数组的长度为n+1
空间复杂度o(n):创建的数组
时间复杂度o(m):只要扫描一遍链表即可
typedef struct Lnode{
int data;
struct Lnode *link;
}List,LNode;
List funt(List L,int n)
{
int * nums=(int*)malloc(sizeof(int)*(n+1));
List tem,pre=L;
int num;
while(L->link)
{
num=L-link->data;
if(nums[num]==0)num[num]=1;
else{
tem=pre->link;
pre->link=pre->next->next;
free(tem);
}
}
free(nums);
return L;
}
2016

思路:
首先满足n1-n2最小,s1-s2绝对值最大,那么我们需要找出最小n1个数,以及最大的n2个数,同时,n1=n/2(向下取整,n1)
采用快速排序,每次排序对元素进行划分,确定一个元素的最终位置,将元素分为左右两部分,左边的都是小于其的右边的都是大于其的。
所以我们需要在快速排序的基础上,尽快的排到第n/2这个位置。
int func(int *nums ,int n)
{
int low=0,high=n-1;
int pre_low=0,pre_high=n-1;//用来保存前一次的low,和high 的值,因为每次排序后,low最终等于high
int mark=n/2,int flag=1;tem;//mark最为最终要排序的点的位置, flag 用来控制循环的进行
while(flag)
{
tem=nums[low];
while(low<high)
{
while(nums[high]>=tem&&low<high)high--;
nums[low]=nums[high];
while(nums[low]<=tem&&low<high)low++;
nums[high]=nums[low];
}
nums[low]=tem;
//排序完一次,查看一下排好的元素的位置与最终位置的差距
if(low=mark){
flag=0;
}
else{
if(low<mark){
low=low+1;
pre_low=low;
high=pre_high;
}
else{
high=low-1;
pre_high=high;
low=pre_low;
}
}
}
int s1=0,s2=0;
for(int i=0;i<n;i++)
{
if(i<=mark)s1=s1+nums[i];
else s2=s2+nums[i];
}
return s2-s1;
}
2017
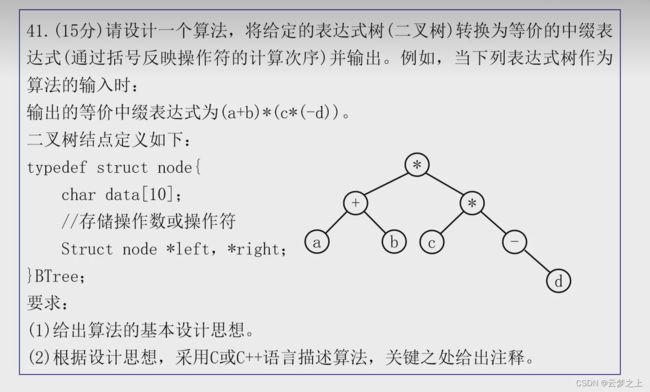
思路
首先二叉树的采用递归的中序遍历
首先,对于每个结点来说,要打印结点的字符串。
然后,对于根节点和叶子结点直接打印字符串,而对于非叶子结点,需要先打印"(“然后打印”)".
所以需要对结点进行区分,区分叶子结点,只需要判断结点的左右子树是否都为空,而判断根节点,非叶结点我们只能引入层数deep变量来加以区分
void func(BTree *root,int deep)
{
if(root->left==NULL&&root->right==NULL)printf("%c",root->data);
else{
if(deep>1)printf("(");
if(root->left!=NULL)func(root->left,deep+1);
prinf("%c",root->data);
if(root->right!=NULL)func(root->right,deep+1);
if(deep>1)printf("(");
}
}
void real(BTree * root)
{
func(root,1);
}
2019

思路
首先找到链表的中点结点
然后对中点后的结点采用头插法进行逆序
然后对中点后的结点按指定位置插入中点前方的结点
维护的变量
p:中间结点
q:用来逆序,以及插入时作为标记后面结点的指针
void reorder(Lnode* head ){
Lnode * p,q,r,s;
p=head;
q=head;
while(q->next){
p=p->next;
q=q->next;
if(q->next)q=q->next;//p每次移动一下,q每次移动两下。假设7个节点,当为奇数个结点时,p移动到了4位置,当为偶数个结点(6)时,p移动到了3
}
保持p结点不变,头插法逆转后续序列
q=p->next;
p->next=NULL;
while(q){
r=q->next//记录下一个要插入的结点
q-next=p->next;
p->next=q;
q=r;
}
s=head->next;//第一个结点
q=p->next;//中点的后一个结点,需要第一个插入到前面的结点
p->next=NULL;//p最终变为为最后的结点,下一节点为空
while(q){
r=q->next;//记录下一个需要插入的结点
q->next=p->next;//先记录p的下一个结点
p->next=q;//p的下一个结点为q
p=q->next;//下一个p为q的next
q=r;
}
}
时间复杂度为O(n),空间复杂度为O(1)
这里需要多次对链表进行操作,需要对头插法实现序列的转置比较熟悉
2020

首先看清题目要求,只是输出最小距离,不需要输出相应的三元组。
这类问题先进行问题的简化,搞清楚我们要求什么。
要使距离D最小,怎么找。
假设a《b《c
那么,D= b-a + c-b + c-a= 2(c-a)也就最大值-最小值的两倍。
那么,要使D最小,我们就要不断的让最小值a向最大值c接近。
假设用a,b,c分别表示3个数组中遍历的数,那么我们每次将其中最小的数的下标后移1,知道某个数组的下标超出数组的长度时停止。
为什么的数不需要计算了?
首先,当一个列表的元素到了末尾,,说明上一次结尾找出的最小值为这个元素的最后一个元素,然后下标进行加1,但此时数组里已经没有元素了。如果,你取其他的数组里的元素,由于数组是从小到大排序的,那么其他数组的后一个元素必然导致与最小值的距离最变大,既c-a变大,相当于a以及不变了,你去移动其他元素。
所以此时得到的就是最小距离了。
#define MAX 9999999;
//计算绝对函数
int abs_(int a,int b){
if(a>b) return a-b;
else return b-a;
}
int calculate(int* s1,int n1,int*s2,int n2,int* s3,int n3){
int i=0,j=0,k=0;
int pre_min=MAX;
int dis=0;
while(i<n1&&j<n2&&k<n3){
dis=abs(s1[i],s2[j])+abs_(s2[j],s3[k])+abs_(s3[j],s1[k]);
if(dis<pre_min){
pre_min=dis;
}
if(s1[i]<s2[j]&&s1[i]<s3[k]){
i++;
}
else if(s2[j]<s3[k]&&s2[j]<s1[i]){
j++;
}
else{
k++;
}
}
return pre_min;
}