【LeetCode热题100】打卡第43天：会议室II&完全平方数

【LeetCode热题100】打卡第43天：会议室II&完全平方数

⛅前言

大家好，我是知识汲取者，欢迎来到我的LeetCode热题100刷题专栏！

精选 100 道力扣（LeetCode）上最热门的题目，适合初识算法与数据结构的新手和想要在短时间内高效提升的人，熟练掌握这 100 道题，你就已经具备了在代码世界通行的基本能力。在此专栏中，我们将会涵盖各种类型的算法题目，包括但不限于数组、链表、树、字典树、图、排序、搜索、动态规划等等，并会提供详细的解题思路以及Java代码实现。如果你也想刷题，不断提升自己，就请加入我们吧！QQ群号：827302436。我们共同监督打卡，一起学习，一起进步。

PS：作者水平有限，如有错误或描述不当的地方，恳请及时告诉作者，作者将不胜感激

会议室II

题目

原题链接：253.会议室II

题解

• 解法一：优先队列

  import java.util.PriorityQueue;
  
  /**
   * @author ghp
   * @title
   */
  class Solution {
      public int minMeetingRooms(int[][] intervals) {
          if (intervals.length == 0) {
              return 0;
          }
          // 升序队列，队头到队尾的元素是从小到大排序的，存储活动的结束时间
          PriorityQueue<Integer> queue = new PriorityQueue<>(intervals.length, (a, b) -> a - b);
          // 往队列中添加第一场会议的结束时间
          queue.offer(intervals[0][1]);
          // 遍历会议的起始时间
          for (int i = 1; i < intervals.length; i++) {
              // 判断当前会议开始时刻，之前开始的会议中是否存在已经结束的会议
              if (intervals[i][0] >= queue.peek()) {
                  // 之前开始的会议中存在已经结束的会议，则将结束的会议从队列中移除
                  queue.poll();
              }
              queue.offer(intervals[i][1]);
          }
          // 所有会议都已经开始了，此时队列中剩余的会议就是存在时间冲突的，需要单独安排会议室
          return queue.size();
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n)$
  • 空间复杂度：$O(n+m)$

  其中 $n$ 为会议的数量，即数组的行，m为数组的列，也就是2

• 解法二：暴力

  感觉这个暴力比优先队列还要难以理解，本题解参考：[中等] 253. 会议室 II - 简书 (jianshu.com)

  个人感觉难以理解的是 end 数组，这个暴力我感觉有点巧妙，end数组表示会议室的数量，还同时记录会议的结束时间，同时表示当前已结束的会议

  import java.util.ArrayList;
  import java.util.Arrays;
  import java.util.List;
  
  /**
   * @author ghp
   * @title
   */
  class Solution {
      public int minMeetingRooms(int[][] intervals) {
          // 记录已结束会议的结束时间
          List<Integer> end = new ArrayList<>();
          // 按开始时间升序
          Arrays.sort(intervals, (a, b) -> a[0] - b[0]);
          // 遍历所有的会议
          for (int[] meeting : intervals) {
              boolean isExit = false;
              // 遍历已结束的会议，判断其中是否存在结束时间早于当前会议起始时间的会议
              for (int i = 0; i < end.size(); i++) {
                  int endTime = end.get(i);
                  if (endTime <= meeting[0]) {
                      // 存在结束时间早于当前会议起始时间的会议，需要更新会议的结束时间
                      end.set(i, meeting[1]);
                      // 找到了当前会议起始时间之前结束的会议，说明不需要新增会议室
                      isExit = true;
                      break;
                  }
              }
              if (!isExit) {
                  // 不存在，说明当前的会议时间与其他会议存在冲突，需要新增会议室
                  end.add(meeting[1]);
              }
          }
          // end中存在的会议都是与其它至少一个会议有冲突的，所以end的大小就是至少需要的会议室数量
          return end.size();
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n^2)$
  • 空间复杂度：$O(n)$

  其中 $n$ 为数组中元素的个数

---

拓展内容

前面我们在解法一中使用优先队列一下就解决了问题，感觉意犹未尽，这里我们提高对自己的要求，我们参考PriorityQueue的源码，直接自己手动实现一个优先队列，顺便学习一下优先队列是如何实现的

class MyPriorityQueue {
    /**
     * 存储队列中的元素
     */
    private int[] arr;
    /**
     * 队列的容量
     */
    private int capacity;
    /**
     * 队列中元素的个数
     */
    private int size;

    public MyPriorityQueue(int capacity) {
        this.arr = new int[capacity];
        this.capacity = capacity;
        this.size = 0;
    }

    /**
     * 添加元素
     * @param val
     */
    public void offer(int val) {
        arr[size] = val;
        size++;
        // 把新加入的元素进行向上调整
        siftUp(arr, size - 1);
    }

    /**
     * 向上调整元素
     * @param arr
     * @param index
     */
    private static void siftUp(int[] arr, int index) {
        int child = index;
        int parent = (child - 1) / 2;
        while (child > 0) {
            if (arr[parent] < arr[child]) {
                // 当前不符合大堆结构，就进行调整
                int temp = arr[parent];
                arr[parent] = arr[child];
                arr[child] = temp;
            } else {
                // 发现当前父节点比子节点大，这时说明整个数组已经符合堆的要求了
                break;
            }
            child = parent;
            parent = (child - 1) / 2;
        }
    }

    /**
     * 移除队尾元素
     * @return
     */
    public int poll() {
        // 下标为0，即队首元素，删除堆顶元素，还要保证剩下的结构依旧为堆
        // 先将队首元素保存下来，先将队首元素保存下来，
        int result = arr[0];
        arr[0] = arr[size - 1];
        size--;
        // 针对队首元素进行向下调整
        siftDown(arr, size, 0);
        // 返回保存的队首元素
        return result;
    }

    private static void siftDown(int[] arr, int size, int index) {
        int parent = index;
        // 通过parent找到child的下标
        int child = 2 * parent + 1;
        while (child < size) {
            //比较左右子树找到较大值
            if (child + 1 < size && arr[child + 1] > arr[child]) {
                child = child + 1;
            }
            // 经过上面的比较已经不知道child是左子树，还是右子树了
            // 但是child下标一定对应左右子树中的较大值下标
            //拿child位置元素与parent位置元素比较
            if (arr[child] > arr[parent]) {
                // 不符合就交换父子节点
                int temp = arr[child];
                arr[child] = arr[parent];
                arr[parent] = temp;
            } else {
                // 调整完毕，不需要再调整
                break;
            }
            // 更新parent和child节点，处理下一层数据
            parent = child;
            child = 2 * parent + 1;
        }
    }

    /**
     * 查看队头元素
     * @return
     */
    public int peek() {
        return arr[0];
    }

    /**
     * 判断队列是否为空
     * @return
     */
    public boolean isEmpty() {
        return size == 0;
    }
}

完全平方数

题目

原题链接：279.完全平方数

题解

• 解法一：DFS（超时 502 / 588 ）

  暴力DFS思路很简单，我们需要提前对数据进行处理，使得这个题目转换成一个求最短路径的问题

  这里举一例例子：

  比如当我们要计算和为12的完全平方数的个数时，我们可以按照以下思路

  1. 计算完全平方数的个数。我们先对12求平方根，可以得出3，这个3就是能够组成和为12的完全平方根的个数
  2. 计算完全平方数。然后根据这个3，我们可以提前计算出12可以由哪些完全平方数组成，很容易可以得到 能够组成12 的完全平方数有：1，4，9
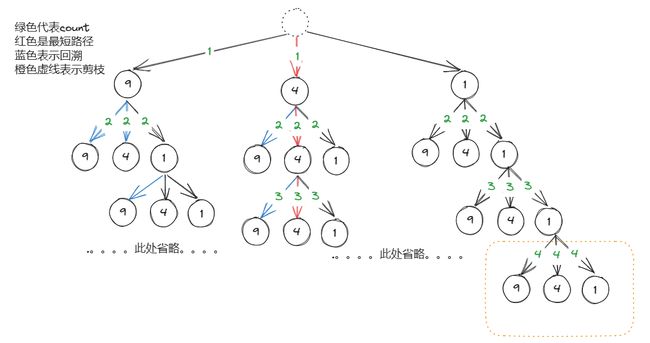
  3. 利用DFS寻找最小组合数，下方是我画的一个比较简单的图解，希望对你的理解有所帮助

  

  /**
   * @author ghp
   * @title
   */
  class Solution {
      // 记录当前和为n的完全平方数的最少数量
      private int min = Integer.MAX_VALUE;
  
      public int numSquares(int n) {
          // 计算完全平方数的个数
          int sqrt = (int) Math.sqrt(n);
          // 计算完全平方数
          int[] square = new int[sqrt];
          for (int i = 1; i <= sqrt; i++) {
              square[i - 1] = i * i;
          }
          // 利用DFS搜寻最短路径
          dfs(square, n, sqrt - 1, 0, 0);
          return min == Integer.MAX_VALUE ? -1 : min;
      }
  
      private void dfs(int[] square, int target, int index, int sum, int count) {
          if (sum == target) {
              // 寻找一种方案，更新min
              min = Math.min(min, count);
              return;
          }
          if (sum > target || count >= min) {
              // 剪枝。当前和已经超过目标值 或 当前参与求和平方数的个数已经大于等于最小值了
              return;
          }
          for (int i = square.length - 1; i > 0; i--) {
              dfs(square, target, i, sum + square[i], count + 1);
          }
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(2^n)$，由于引入了剪枝操作实际的耗时会比理论上的低
  • 空间复杂度：$O(n)$

  其中 $n$ 为square数组中元素的个数

  代码优化：（优化后还是超时 551 / 588）

  1. 去除了count和isFind等成员变量，直接采用变量的引用传递。直接进行变量的引用传递通常比使用成员变量要更好，因为这样可以减少对成员变量的访问开销，并且可以避免多线程环境下的竞争和同步问题。而且，使用引用传递可以使代码更清晰和易读。
  2. 在dfs方法中增加了一个剪枝条件，当当前步数count已经大于等于min时，停止继续搜索
  3. 在dfs方法中增加了一个next变量，记录下一层最大的值，优化了循环次数（核心优化）

  这个 next 能够使得快速定位到下一个数，比如：square=1，4，9，target=12，第一遍index=2，sum=0，此时 next= (12-0)/9=1，下一层遍历就直接从索引为1开始，直接对索引大于1的进行了一个剪枝

  

  /**
   * @author ghp
   * @title
   */
  class Solution {
      // 记录当前和为n的完全平方数的最少数量
      private int min = Integer.MAX_VALUE;
  
      public int numSquares(int n) {
          // 计算完全平方数的个数
          int sqrt = (int) Math.sqrt(n);
          // 计算完全平方数
          int[] square = new int[sqrt];
          for (int i = 1; i <= sqrt; i++) {
              square[i - 1] = i * i;
          }
          // 利用DFS搜寻最短路径
          dfs(square, n, sqrt - 1, 0, 0);
          return min == Integer.MAX_VALUE ? -1 : min;
      }
  
      private void dfs(int[] square, int target, int index, int sum, int count) {
          if (sum == target) {
              // 寻找一种方案，更新min
              min = Math.min(min, count);
              return;
          }
          if (index < 0 || count >= min) {
              // 剪枝。已经到最底层了 或 当前参与求和平方数的个数已经大于等于最小值了
              return;
          }
          // 计算下一层的最大节点
          int maxCount = (target - sum) / square[index];
          for (int i = maxCount; i > 0; i--) {
              dfs(square, target, index - 1, sum + i * square[index], count + i);
          }
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(2^n)$，由于引入了剪枝操作实际的耗时会比理论上的低
  • 空间复杂度：$O(n)$

  其中 $n$ 为square数组中元素的个数

  代码优化：（过啦）

  我们可以发现之前那种先把所有能够组成n的平方和求出的方式比较蠢，既浪费了空间又浪费了时间，我们完全可以在一边DFS遍历的时候，一遍计算平方和，从最大数到最小数开始搜索。解题的图解和前面的是一致的，就是节约了求取平方和的操作，从而大大节约的时间，但是可以发现这样子，能过，提交后空间占比超过该90%，时间占比只超过5%，所以说这一题DFS并不是终极解法

  class Solution {
      private int minCount = Integer.MAX_VALUE;
  
      public int numSquares(int n) {
          dfs(n, 0);
          return minCount;
      }
  
      private void dfs(int target, int count) {
          if (count >= minCount) {
              // 如果当前数量已经超过最小数量，则直接返回
              return;  
          }
          if (target == 0) {
              // 如果目标数为0，更新最小数量并返回
              minCount = Math.min(minCount, count);
              return;  
          }
          for (int i = (int) Math.sqrt(target); i > 0; i--) {
              // 尝试使用完全平方数进行递归搜索
              dfs(target - i * i, count + 1);  
          }
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(2^n)$，由于引入了剪枝操作实际的耗时会比理论上的低
  • 空间复杂度：$O(n)$

  其中 $n$ 为square数组中元素的个数

• 解法二：BFS（超时 502 / 588 ）

  一般DFS的题目都可以使用BFS解决，同时对于最短路径问题，一般BFS要比DFS要更加快。这里吸取前面的经验，来使用BFS实现

  import java.util.Deque;
  import java.util.LinkedList;
  
  /**
   * @author ghp
   * @title
   */
  class Solution {
  
      public int numSquares(int n) {
          Deque<int[]> queue = new LinkedList<>();
          queue.offer(new int[]{0, 0});
          while (!queue.isEmpty()) {
              // 上一层节点的状态
              int[] pre = queue.poll();
              int sum = pre[0];
              int count = pre[1];
              if (sum == n || count == min) {
                  // BFS一层一层往下搜，最先等于n的，一定是最段路径，所以这里直接就返回了
                  return count;
              }
              // 遍历下一层
              for (int i = (int) Math.sqrt(n); i > 0; i--) {
                  if (sum + i * i <= n) {
                      queue.offer(new int[]{sum + i * i, count + 1});
                  }
              }
          }
          return -1;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n^{1.5})$，在每一层中，内层循环的次数是随着当前节点的值而减少的，即与n有关的次数。每个节点最多可以生成n个节点，因此总共的节点个数是n^1.5级别的。
  • 空间复杂度：$O(n)$，主要是用来存储队列和集合的空间消耗，并且最坏情况下，所有的数都需要存储在vis集合中

  其中 $n$ 为square数组中元素的个数

  对于最短路径问题，一般BFS要比DFS能容易找到答案

  代码优化：（过啦）

  直接暴力BFS不能过，我们可以进行记忆化搜索从而实现剪枝效果，

  import java.util.Deque;
  import java.util.HashSet;
  import java.util.LinkedList;
  import java.util.Set;
  
  class Solution {
  
      public int numSquares(int n) {
          Deque<int[]> queue = new LinkedList<>();
          // 记录搜索的状态
          Set<Integer> vis = new HashSet<>();
          queue.offer(new int[]{0, 0});
          while (!queue.isEmpty()) {
              // 上一层节点的状态
              int[] pre = queue.poll();
              int sum = pre[0];
              int count = pre[1];
              if (sum == n || count == min) {
                  // BFS一层一层往下搜，最先等于n的，一定是最段路径，所以这里直接就返回了
                  return count;
              }
              // 遍历下一层
              for (int i = (int) Math.sqrt(n); i > 0; i--) {
                  int curSum = sum + i * i;
                  if (!vis.contains(curSum) && curSum <= n) {
                      // 当前层的状态并没有出现，并且当前和也要小于目标值，则可以往下遍历
                      queue.offer(new int[]{curSum, count + 1});
                      // 将当前状态添加到vis集合中
                      vis.add(curSum);
                  }
              }
          }
          return -1;
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n^{1.5})$，在每一层中，内层循环的次数是随着当前节点的值而减少的，即与n有关的次数。每个节点最多可以生成n个节点，因此总共的节点个数是n^1.5级别的。
  • 空间复杂度：$O(n)$，主要是用来存储队列和集合的空间消耗，并且最坏情况下，所有的数都需要存储在vis集合中

  其中 $n$ 为square数组中元素的个数

  ---

  这里再提供一种方法，参考这位大佬的，我感觉这个BFS解法相当优雅，这里是直接通过 sqrt 计算出下一层节点的最大值，从而不需要遍历所有的可能，不需要像上面那种方法还单独拿一个 vis 去记录状态，使用 sqrt计算后 压根就不需要去当心会有重复状态的出现，它相当于是跳跃式的遍历，这个有点类似与我之前 DFS 中的方法，至少在DFS我想到了，在这里我又没想到w(ﾟДﾟ)w

  import java.util.LinkedList;
  import java.util.Queue;
  
  class Solution {
      public int numSquares(int n) {
          // 队列记录剩余值
          Queue<Integer> queue = new LinkedList<>();
          queue.add(n);
          int count = 0;
          while (!queue.isEmpty()) {
              count++;
              for (int size = queue.size(); size > 0; size--) {
                  // 回溯到上一个节点
                  int pre = queue.poll();
                  // 计算下一层最大的值
                  int next = (int) Math.sqrt(pre);
                  if (next * next == pre) {
                      return count;
                  }
                  for (int i = next; i > 0; i--) {
                      queue.add(pre - i * i);
                  }
              }
          }
          return -1;
      }
  }
  

• 解法三：动态规划

  本题本质是一个完全背包问题，我们完全可以参考完全背包问题的解法进行求解

  题解参考：【宫水三叶】详解完全背包一维空间优化推导（附背包问题攻略） - 完全平方数 - 力扣（LeetCode）

  import java.util.Arrays;
  
  class Solution {
      int INF = 0x3f3f3f3f;
  
      public int numSquares(int n) {
          // 计算出所有可能用到的完全平方数
          int m = (int) Math.sqrt(n);
          int[] square = new int[m];
          for (int i = 1; i <= m; i++) {
              square[i - 1] = i * i;
          }
          // f[i][j] 代表考虑前 i 个物品，凑出 j 所使用到的最小元素个数
          int[][] f = new int[m + 1][n + 1];
          // 当没有任何数时，除了 f[0][0] 为 0（花费 0 个数值凑出 0），其他均为无效值
          Arrays.fill(f[0], INF);
          f[0][0] = 0;
          // 处理剩余数的情况
          for (int i = 1; i <= m; i++) {
              int x = square[i - 1];
              for (int j = 0; j <= n; j++) {
                  // 对于不选第 i 个数的情况
                  f[i][j] = f[i - 1][j];
                  // 对于选 k 次第 i 个数的情况
                  for (int k = 1; k * x <= j; k++) {
                      // 能够选择 k 个 x 的前提是剩余的数字 j - k * x 也能被凑出
                      if (f[i - 1][j - k * x] != INF) {
                          f[i][j] = Math.min(f[i][j], f[i - 1][j - k * x] + k);
                      }
                  }
              }
          }
          return f[m][n];
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n^2\ast \sqrt{n})$
  • 空间复杂度：$O(n\ast \sqrt{n})$

  其中 $n$ 为square数组中元素的个数

  代码优化：空间优化

  备注：这里我先把题解放这里，今天就先把DFS和BFS的两个解法给消化吸收了，这个动态规划，我把题解和链接先放这里，后面二刷或者后面有时间的时候再来看一看，同样的这个题解也来自【宫水三叶】大佬

  二维转一维

  class Solution {
      public int numSquares(int n) {
          int[] f = new int[n + 1];
          Arrays.fill(f, 0x3f3f3f3f);
          f[0] = 0;
          for (int t = 1; t * t <= n; t++) {
              int x = t * t;
              for (int j = x; j <= n; j++) {
                  f[j] = Math.min(f[j], f[j - x] + 1);
              }
          }
          return f[n];
      }
  }
  

  复杂度分析：

  • 时间复杂度：$O(n^{\ast }\sqrt{n})$
  • 空间复杂度：$O(\sqrt{n})$

  其中 $n$ 为square数组中元素的个数

• 解法四：四平方和定理

  这是本题的究极解法了，感兴趣的可以去LeetCode官方看看（果然算法的尽头就是数学）

  class Solution {
      public int numSquares(int n) {
          if (isPerfectSquare(n)) {
              return 1;
          }
          if (checkAnswer4(n)) {
              return 4;
          }
          for (int i = 1; i * i <= n; i++) {
              int j = n - i * i;
              if (isPerfectSquare(j)) {
                  return 2;
              }
          }
          return 3;
      }
  
      // 判断是否为完全平方数
      public boolean isPerfectSquare(int x) {
          int y = (int) Math.sqrt(x);
          return y * y == x;
      }
  
      // 判断是否能表示为 4^k*(8m+7)
      public boolean checkAnswer4(int x) {
          while (x % 4 == 0) {
              x /= 4;
          }
          return x % 8 == 7;
      }
  }
  
  作者：LeetCode-Solution
  链接：https://leetcode.cn/problems/perfect-squares/solution/wan-quan-ping-fang-shu-by-leetcode-solut-t99c/
  来源：力扣（LeetCode）
  著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。
  

  复杂度分析：

  • 时间复杂度：$O(\sqrt{n})$
  • 空间复杂度：$O(1)$

参考题解：

• 完全平方数 - 完全平方数 - 力扣（LeetCode）
• 画解算法：279. 完全平方数 - 完全平方数 - 力扣（LeetCode）
• 【宫水三叶】详解完全背包一维空间优化推导（附背包问题攻略） - 完全平方数 - 力扣（LeetCode）
• 标准的 BFS 题解 - 完全平方数 - 力扣（LeetCode）

在此致谢各位LeetCode的大佬