栈抽象数据类型以及Python实现
栈抽象数据类型以及Python实现
一、什么是栈?
一种有次序的数据项集合,在栈中,数据项的加入和移除都仅发生在同一端。(这一端叫栈顶Top,另一端叫栈底 base)
日常生活中有很多栈的应用:盘子、托盘、书堆等等。
二、栈的特点
1.距离栈底越近的数据项,留在栈中的时间就越长,而最新加入栈的数据项会被最先移除。
☆这种次序通常称之为==“后进先出LIFO”==: Last in First out
这是一种基于数据项保存时间的次序,时间越短的离栈顶越近,时间越长的离栈底越近。
2.进栈和出栈的次序正好相反
三、抽象数据类型Stack
抽象数据类型栈Stack:是一个有次序的数据集,每个数据项仅从栈顶一端加入到数据集中、从数据集中移除(只在一端进行操作),栈具有后进先出LIFO的特性。
抽象数据类型栈Stack定义为 如下操作:
Stack(): 创建一个空栈,不包含任何数据项
push(item): 将item加入栈顶,无返回值
pop(): 将栈顶数据项移除,并返回,栈被修改
peek(): 返回栈顶的数据项但不移除,栈不被修改
isEmpty: 返回栈是否为空栈
size(): 返回栈中有多少个数据项
四、用Python实现ADT Stack
将ADT Stack实现为Python的一个Class;
将ADT Stack的操作实现为Class的方法,使用数据集List来实现。
☆ Stack的两端对应list设置:可以将List的任意一端(index = 0 or index = -1)设置成栈顶
1.采用List的末端(index = -1)来作为栈顶,通过对list的append 和 pop来实现栈的操作。
> 在栈顶尾端实现的stack,push 和 pop 的复杂度为O(1)
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items) - 1]
def size(self):
return len(self.items)
s = Stack()
print(s.isEmpty()) # True
s.push(5)
s.push('hello')
print(s.peek()) # hello
s.push(True)
print(s.size()) # 3
print(s.isEmpty()) # False
s.push(500)
print(s.pop())
print(s.pop())
print(s.size()) # 2
# 使用for循环遍历打印列表中的值(即目前栈中元素)
for _ in range(s.size()):
print(s.items[_], end=' ')
-
在栈顶首端实现的 push 和 pop 的复杂度是O(n) : index = 0 作为栈顶。
class Stack: def __init__(self): self.items = [] def isEmpty(self): return self.items == [] def push(self, item): self.items.insert(0, item) # index = 0 为栈顶, push 和 pop 操作都在 列表的首端 def pop(self): return self.items.pop(0) def peek(self): return self.items[0] def size(self): return len(self.items)虽然不同的实现方案时间复杂度不同,但是都保持了ADT接口的稳定性。
五、栈的应用
1.通用括号匹配
每一个左括号必须匹配一个右括号,括号的使用必须配套。
从左到右,最新打开的左括号,应该匹配到最先遇到的右括号。
最早打开,匹配最后遇到。
class Stack:
def __init__(self):
self.items = []
def isEmpty(self):
return self.items == []
def push(self, item):
self.items.append(item)
def pop(self):
return self.items.pop()
def peek(self):
return self.items[len(self.items) - 1]
def size(self):
return len(self.items)
def parChecker(symbolString):
s = Stack() # 实例化对象 栈s
balanced = True
index = 0
while index < len(symbolString) and balanced:
# 遍历字符串,遇到左括号进行入栈操作
symbol = symbolString[index]
# if symbol == "(":
if symbol in "({[":
# 匹配所有类型的括号
s.push(symbol)
else: # 遇到右括号,先查看栈是否为空,为空则代表右括号是多出来的,匹配失败
if s.isEmpty():
balanced = False
else: # 栈不为空,令top等于栈顶元素,使用matches函数匹配
top = s.pop()
if not matches(top, symbol):
balanced = False
index = index + 1
if balanced and s.isEmpty():
return True
else:
return False
def matches(top, symbol):
opens = "([{"
closers = ")]}"
return opens.index(top) == closers.index(symbol)
# 字符串 index() 方法查找指定值的首次出现的位置,位置相同,代表括号匹配
print(parChecker('()()()((())'))
print(parChecker('()(())'))
print(parChecker('{{[[}'))
print(parChecker('([{}])'))
2.十进制转换二进制
除以2的过程,得到的余数是从低到高的顺序,而输出则是从高到低,所以需要一个栈来反转次序。
def divideBy2(decNumber, base):
"""
十进制转换为十六以下任意进制, base 接收传入的进制,例如2,8,16
:param decNumber: 待转换的数字
:param base: 进制
:return: 转换好的数字进制
"""
digits = "0123456789ABCDEF"
remstack = Stack()
while decNumber > 0:
rem = decNumber % base
remstack.push(rem)
decNumber //= base
newString = ""
while not remstack.isEmpty():
newString += digits[remstack.pop()]
return newString
# 8 转船为2进制, 1000
print(divideBy2(8, 2))
# 300 转换成16进制 , 12C
print(divideBy2(300, 16))
# 32 转换成8进制, 40
print(divideBy2(32, 8))
3.中缀表达式转换为前缀和后缀形式
无论表达式多么复杂,需要转换成前缀或者后缀,只需要两个步骤:
①将中缀表达式转换成 全括号形式
② 将所有的操作符移动到子表达式所在的左括号(前缀) 或者 ==右括号(后缀)==处,替代后再删除所有的括号
☆ 通用的中缀转后缀算法
在中缀表达式转换为后缀形式的处理过程中,操作符比操作数要晚输出,所以在扫描到对应的第二个操作数之前,需要把操作符先保存起来。
这些暂存的操作符,由于优先级的规则,还有可能要反转次序输出。(例如在A+B*C中,+ 虽然先出现, 但是优先级比后面的 * 要低,故要等 * 处理完后才能再处理。)
由于这种反转特性,所以考虑使用Stack栈来保存暂时未处理的操作符。
再来看(A+B)* C ,对应的后缀形式是 AB+C* , 这里的 + 的输出比 * 要早,主要是因为括号使得 + 的优先级提升了,高于括号外的 * 。所以,遇到左括号,要进行标记下,其后出现的操作符优先级提升了,一旦扫描到相应的右括号,就马上输出这个操作符。
栈顶的操作符 是最近暂存进去的,当遇到一个新的操作符,就需要跟栈顶的操作符比较下优先级,再进行处理。
"""
中缀表达式转后缀表达式算法流程:
规定:中缀表达式由空格隔开的一系列单词(token)构成。
1. 创建空栈opstack用于暂存操作符,空表postfixList用于保存后缀表达式
2. 将中缀表达式转换成单词(token)列表, split()
3. 从左到右扫描中缀表达式的单词列表:
若单词是操作数或者空格,则直接添加到后缀表达式列表的末尾。
若单词是左括号“(”,则压入opstack栈顶
若单词是右括号“)”,则反复弹出opstack栈顶的操作符,加入到列表末尾,直到遇见左括号。
若单词是操作符“*/+-”,则压入opstack栈顶:
压入之前,比较其与栈顶操作符的优先级,若栈顶的操作符优先级 高于或者等于 它,那么反复弹出栈顶操作符,加入到输出列表末尾,直到栈顶的操作符优先级低于它。
4. 中缀表达式单词列表扫描结束后,把opstack栈中所有剩余操作符 依次弹出,添加到输出列表末尾。
5. 把输出列表再用 join 方法合并成后缀表达式字符串,算法结束。
"""
"""
中缀表达式转后缀表达式!
约定:使用空格 分隔操作数与操作符
"""
def infixTopostfix(infixexpr):
prec = {"*": 3, "/": 3, "+": 2, "-": 2, "(": 1}
# 记录操作符的优先级
opStack = Stack()
postfixList = []
tokenList = infixexpr.split()
# 默认分隔符为空格
print(tokenList)
# 将中缀表达式解析到列表中
for token in tokenList:
if token in "ABCDEFGHIJKLMNOPQRSTUVWXYZ" or token == " ":
postfixList.append(token)
elif token == '(':
opStack.push(token)
elif token == ')':
topToken = opStack.pop()
while topToken != '(':
postfixList.append(topToken)
topToken = opStack.pop()
else:
while (not opStack.isEmpty()) and \
(prec[opStack.peek()]) >= prec[token]:
postfixList.append(opStack.pop())
opStack.push(token)
while not opStack.isEmpty():
postfixList.append(opStack.pop())
print(postfixList)
return ' '.join(postfixList)
str1 = 'A + B * C + ( D * E + F ) * G'
print(type(str1))
print(infixTopostfix(str1))
# A B C * + D E * F + G * +
-
计算后缀表达式的值:
后缀操作符在操作数的后面,所以要暂存操作数,在碰到操作符的时候,再将暂存的两个操作数进行实际的运算。
先入栈的是 左边的数, 后入栈的是右操作数 , 不影响加乘, 影响 减除
"""
流程:
1.创建空栈openrandStack用于暂存操作数
2.将后缀表达式用split方法解析为单词(token)列表
3.从左到右扫描单词列表:
若单词是操作数,将单词转换成整数int,压入operandStack栈顶
若单词是操作符,就开始求值,从栈顶弹出两个操作数,先弹出右操作数,后弹出左操作数,计算后将值重新压入栈顶。
4.单词列表扫描结束后,表达式的值就在栈顶。
5.弹出栈顶的值,返回。
"""
def evaluapostfix(expression):
openrandStack = Stack()
tokenList = expression.split()
for token in tokenList:
if token in '0123456789' or token == ' ':
openrandStack.push(int(token))
else:
op2 = openrandStack.pop()
op1 = openrandStack.pop()
openrandStack.push(calvalue(token, op1, op2))
return openrandStack.pop()
def calvalue(sign, op1, op2):
if sign == '*':
return op1 * op2
elif sign == '+':
return op1 + op2
elif sign == '/':
return op1 / op2
elif sign == '-':
return op1 - op2
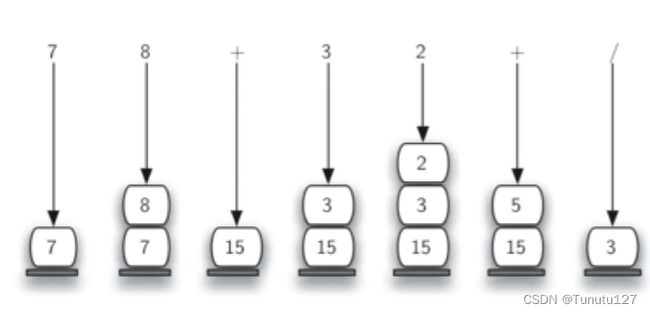
str = '7 8 + 3 2 + /'
print(evaluapostfix(str))
# result == 3
5.洗碗工
洗碗工小明碰上了一个强迫症老板老王,餐厅一共就10只盘子,老板给仔细编上了0~9等10个号码,并要求小明按照从0到9的编号顺序来洗盘子,当然,每洗好一只盘子,就必须得整齐叠放起来。
小明洗盘子期间,经常就有顾客来取盘子,当然每位顾客只能从盘子堆最上面取1只盘子离开。
老王在收银台仔细地记录了顾客依次取到盘子的编号,比如"1043257689",这样他就能判断小明是不是遵循命令按照0123456789的次序洗盘子了。
你也能像老王一样作出准确的判断吗?
# 判断出栈序列是否可以实现(找出不可能的出栈序列)
def is_wash(s):
st = Stack()
# 正在洗的盘子编号 n
n = 0
# 取盘子的顺序,s[i]是取得盘子的编号
i = 0
while i < 10 and n < 10:
k = int(s[i])
# 洗盘子,若顾客取到k盘子,则正在洗的n 到 k 之间 都已洗好
if n <= k:
for m in range(n, k + 1):
st.push(m)
n = k + 1
# 取盘子, 若从k开始取,一直取到对不上好,说明要取的还没洗
while not st.isEmpty() and st.peek() == int(s[i]):
m = st.pop()
i += 1
if st.isEmpty():
print("Yes!")
else:
print("No!")
s = '1043257689'
is_wash(s)
# Yes!