LeetCode精选TOP面试题（中等篇）【出现率降序】

143. 重排链表

（递归）

第一种方法我们可以使用递归的方式处理链表，即我们只需要处理头结点的逻辑，其他的节点只需要递归完成即可。

既然是要一个头结点一个尾节点，那么我们就可以手动地找到链表的尾结点，然后将head节点指向tail节点即可。至于(head, tail)中点的节点就可以递归按照这种逻辑处理即可。

而且可以发现如果一个链表的节点数量小于等于2的话，就可以不用处理直接返回了，所以if (!head || !head->next || !head->next->next) return head;。

class Solution {
public:
    ListNode* reorder(ListNode* head) {
        if (!head || !head->next || !head->next->next) return head;
        ListNode* cur = head;
        while (cur->next->next) {
            cur = cur->next;
        }
        ListNode* next = head->next;
        ListNode* tail = cur->next;
        head->next = tail;
        cur->next = nullptr;
        tail->next = reorder(next);
        return head;
    }

    void reorderList(ListNode* head) {
        head = reorder(head);
    }
};

（找链表中点+反转链表+合并链表）

本题的难点就在于我们容易将这种链式结构一头一尾的将节点取出，所以使用递归的方式其实可以帮助我们跳过中间的节点而找到尾结点。

而如果我们就是想要使用迭代的方式完成链表的重排的话，我们就必须要解决从尾到头的方式获取节点。其实我们可以使用一个vector将节点都放入数组中，这样就可以从尾到头的获取节点了。但是这样就会浪费O(N)的空间。如果我们想要从尾到头的获取节点的话，其实可以通过反转链表的方式实现。然后再通过二路归并从两个链表中交替获取节点。

所以本题的思路就是反转一半的链表，再二路归并两个链表。而反转一半的链表就要先找到链表的中点，然后再通过迭代的方式反转链表。

class Solution {
public:
    void reorderList(ListNode* head) {
        // 只遍历一次找到链表中点
        ListNode* fast = head, *slow = head;
        while (fast && fast->next) {
            slow = slow->next;
            fast = fast->next->next;
        }
        ListNode* tail = slow->next;
        slow->next = nullptr;
        // 迭代版反转链表
        ListNode* t1 = nullptr;
        while (tail) {
            ListNode* next = tail->next;
            tail->next = t1;
            t1 = tail;
            tail = next;
        }
        // 找到规律合并链表
        ListNode* t2 = head;
        ListNode* dummy = new ListNode(0);
        ListNode* cur = dummy;
        while (t1 && t2) {
            cur = cur->next = t2;
            t2 = t2->next;
            cur = cur->next = t1;
            t1 = t1->next;
        }
        cur->next = t2;
    }
};

525. 连续数组

（前缀和+哈希表）

我们需要找到一段区间中0和1的数量相同，最直接的想法就是我们需要将一段区间中的0和1的数量都求出来，然后判断是否相同即可。求出一段区间中的0和1的数量可以使用前缀和的思想将时间复杂度从O(N)降到O(1)。而且如果相比较出出一段区间中的0和1的数量可以不用两个前缀和数组来比较，可以使用一个前缀和数组表示0和1的个数的差值即可，如果结果为0就说明0和1的个数相同，否则0和1的个数不同。

但是即使解决了一段区间中的0和1的个数，但是我们还是需用两层循环去枚举数组中所有连续的区间，这样还是会超时。

我们再来看看计算一段区间中的1和0的数量的公式。[i, i], [i, i - 1], ..., [i, 1]，我们需要枚举出i个区间，但是我们只是要求出是否在前i个数组成的区间中存在和前j个数组成的区间中0和1的个数的差值是相同的。所以就可以使用一个哈希表判断s[i]是否存在在哈希表中，并且将前i个数字组成的差值放入哈希表中等待查询即可。

如果数组的下标从1开始的话，那么没有数字组成的区间中0和1个数的差值为0，即hash[0] = 0。

class Solution {
public:
    int findMaxLength(vector<int>& nums) {
        unordered_map<int, int> hash;
        int ans = 0;
        int count = 0;
        int n = nums.size();
        hash[0] = 0;
        for (int i = 1; i <= n; i ++) {
            count += nums[i - 1] == 1 ? 1 : -1;
            if (hash.count(count)) {
                ans = max(ans, i - hash[count]);
            } else {
                hash[count] = i;
            }
        }
        return ans;
    }
};

50. Pow(x, n)

（快速幂）

如果我们想要求出一个数字的n次方的话，如果一个一个乘就太慢了。因为n有多大，num就需要乘以一个自身n次。所以我们可以观察是否可以简化这个过程。

我们通常使用位运算的方式简化计算，如果计算num的n次方的话，那么我们只需要将n对应的二进制列出来即可。而n的二进制的位置就是ans需要乘的num的位数。所以我们可以预处理出num²,num⁴,num⁸,…，而numⁿ=num^1+2+4+…+。所以我们就将乘以n次方转化为了n的二进制位数次。

为什么可以想到这种方法？

因为如果想要对一个数字乘方计算进行简化的话，我们只能从n次方入手，而我们需要观察出n的特性，可以发现n可以拆解成二进制的形式计算，每一次通过乘方就是扩大平方倍，而每一个数字都是同二进制，即1,2,4,8…这些数构成的，所以我们通过这种方式对n进行简化计算。

class Solution {
public:
    double myPow(double x, int n) {
        typedef long long LL;
        bool flag = n < 0;
        double ans = 1;
        for (LL k = (LL)abs(n); k; k >>= 1) {
            if (k & 1) ans = ans * x;
            x *= x;
        }
        if (flag) return 1.0 / ans;
        else return ans;
    }
};

class Solution {
public:
    double myPow(double x, int n) {
        typedef long long LL;
        double ans = 1;
        bool flag = n < 0;
        LL k = abs(n);
        while (k) {
            if (k & 1) {
                ans = ans * x;
            }
            k >>= 1;
            x *= x;
        }
        if (flag) return 1.0 / ans;
        else return ans;
    }
};

18. 四数之和

（递归回溯）

最暴力的方法就是利用回溯算法，将nums数组中的数字每4个为一个组合，求出全部的组合方式。虽然中间使用了剪枝和判重的技巧，但是这样的时间复杂度还是指数级别的，所以还是会超时。

class Solution {
public:
    vector<vector<int>> ans;
    vector<int> path;
    typedef long long LL;
    void dfs(vector<int>& nums, LL target, int index) {
        if (path.size() == 4) {
            if (target == 0)
                ans.push_back(path);
            return ;
        }
        int n = nums.size();
        if (index + 4 - path.size() > n) return ; // 剪枝
        for (int i = index; i < n; i ++) {
            if (i != index && nums[i] == nums[i - 1]) continue;
            path.push_back(nums[i]);
            dfs(nums, target - nums[i], i + 1);
            path.pop_back();
        }
    }

    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        sort(nums.begin(), nums.end());
        dfs(nums, target, 0);
        return ans;
    }
};

（双指针）

根据上面的经验，我们可以知道如果暴力四层循环一定也是不可以的，所以我们可以利用双指针的思想将数组先排序，然后两层循环枚举前面两个数字，nums[i], nums[j]。后面两个数字的和就是target - nums[i] - nums[j]了，这个时候数组就有了单调性，就可以使用双指针算法了。

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        typedef long long LL;
        sort(nums.begin(), nums.end());
        int n = nums.size();
        vector<vector<int>> ans;
        if (n < 4) return ans; // 剪枝
        for (int i = 0; i < n - 1; i ++) {
            if (i && nums[i] == nums[i - 1]) continue; // 避免重复元素
            for (int j = i + 1; j < n - 2; j ++) {
                if (j != i + 1 && nums[j - 1] == nums[j]) continue; // 避免重复元素
                // 双指针
                int l = j + 1, r = n - 1;
                LL sum = nums[i] + (LL)0 + nums[j] + nums[l] + nums[r];
                while (l < r) {
                    if (sum < target) l ++;
                    else if (sum > target) r --;
                    else {
                        ans.push_back({nums[i], nums[j], nums[l], nums[r]});
                        l ++, r --;
                        while (l < r && nums[l] == nums[l - 1]) l ++;
                        while (l < r && nums[r] == nums[r + 1]) r --; 
                    }
                    sum = nums[i] + (LL)0 + nums[j] + nums[l] + nums[r];
                }
            }
        }
        return ans;
    }
};

class Solution {
public:
    vector<vector<int>> fourSum(vector<int>& nums, int target) {
        typedef long long LL;
        int n = nums.size();
        vector<vector<int>> ans;
        if (n < 4) return ans;
        sort(nums.begin(), nums.end());
        for (int i = 0; i < n; i ++) {
            if (i && nums[i] == nums[i - 1]) continue;
            for (int j = i + 1; j < n; j ++) {
                if (j != i + 1 && nums[j] == nums[j - 1]) continue;
                for (int l = j + 1, r = n - 1; l < r; l ++) {
                    if (l != j + 1 && nums[l] == nums[l - 1]) continue;
                    while (r - 1 > l && 
                     nums[i] + nums[j] >= (LL)target - nums[l] - nums[r - 1]) r --;
                    if (nums[i] + nums[j] == (LL)target - nums[l] - nums[r]) {
                        ans.push_back({nums[i], nums[j], nums[l], nums[r]});
                    }
                }
            }
        }
        return ans;
    }
};

总结：两数之和，三数之和，四数之和。

三数之和和四数之和都是同一类型的题目，都是因为暴力循环不能解决问题，然后通过数组排序使得数组具有单调性。这样就可以使用双指针算法让查找的效率变成O(N)。

我们发现哈希表应用在两数之和中可以使得查找的效率变成O(1)，但是因为两数之和要求出数字在原数组中的下标，所以不能使用排序+双指针来实现。

所以我们知道了通过排序+双指针的算法可以将O(N²)的查找降为O(N)的查找。而哈希表一般只适用于两数之和为target的情况下，否则枚举数字没有办法解决问题。

162. 寻找峰值

（暴力）

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int n = nums.size();
        for (int i = 1; i < n - 1; i ++) {
            if (nums[i] > nums[i + 1] && nums[i] > nums[i - 1]) return i;
        }
        return nums.back() > nums[0] ? n - 1 : 0;
    }
};

（二分）

因为我们只需要求出一个峰值的下标即可。所以我们就可以把数组当做只有一个峰值。可以发现其实峰值的特点就是比左右两边的值都要大。但是如果只是抓住这一点的话，我们也就只能顺序查找一个值。我们可以将这个点看成是“下坡”的第一个点，这样峰值的前面都是单调递增，后面都是单调递减，这样划分的话，数组就具有了二段性，我们就可以使用二分来解决这个问题了。

总结：由本题可知二分的本质是「二段性」而不是「单调性」。本题就是可以有多个峰值，但是我们可以找到其中一个峰值。只需要有一个将一段数组划分成为两段的性质即可。

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int n = nums.size();
        int l = 0, r = n - 1;
        while (l < r) {
            int mid = l + (r - l) / 2;
            if (mid + 1 < n && nums[mid] > nums[mid + 1]) r = mid;
            else l = mid + 1;
        }
        return l;
    }
};

（三分）

三分的基本原理是根据画图推出来的规律，int mid1 = l + (r - l) / 3;int mid2 = r - (r - l) / 3;。如果nums[mid1] > nums[mid2]的话，那么无论mid1在峰值的左边还是峰值的右边，[mid2, r]一定都不存在峰值，因为如果峰值在[mid2, r]中间的话，那么nums[mid2]一定大于nums[mid1]，所以根据这种三分的方法我们就可以排除1/3的部分。同理if(nums[mid2] >= nums[mid1])，那么[l, mid1]中一定不存在峰值。

这种三分的方法是专门用来求出峰值的。

class Solution {
public:
    int findPeakElement(vector<int>& nums) {
        int n = nums.size();
        int l = 0, r = n - 1;
        while (l < r) {
            int mid1 = l + (r - l) / 3;
            int mid2 = r - (r - l) / 3;
            if (nums[mid2] > nums[mid1]) l = mid1 + 1;
            else r = mid2 - 1;
        }
        return l;
    }
};

881. 救生艇

（贪心+双指针）

如果是站在做题的角度来说的话，数据范围是500000，所以一般暴力方法一定是过不了的，因此题解不是动规就是贪心。

本题需要使得船的数量最少。我们观察到如果想要求出第i个人或者前i个人所需的最少船的数量的话，没有一个子问题可以描述出来，也就是和前面一个人没有关系，所以本题不能使用贪心。

所以我们贪心地想，如果想要使得船数最少，那么每一次尽量每艘船上都尽可能的多带人。所以我们可以想到先将数组排序，因为people[i] < limit的，所以从前往后的每一个人一定都可以自己单独一条船。然后每一次如果people(最轻) + people(最重) <= limits的话，那么两个人共用一条船一定是最省的，反之就重的的人自己一条船即可。

这样每一次都将最重的人考虑在内，使得每条船在全局和局部都是最优解，这样就是贪心的解法。

class Solution {
public:
    int numRescueBoats(vector<int>& people, int limit) {
        int n = people.size();
        sort(people.begin(), people.end());
        int l = 0, r = n - 1;
        int ans = 0;
        while (l <= r) {
            if (people[r] + people[l] > limit) r --;
            else l ++, r --;
            ans ++;
        }
        return ans;
    }
};

59. 螺旋矩阵 II

（偏移量）

我们只需要根据偏移量的设置使得数字在数组中顺时针旋转即可。

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
       int xd[4] = {0, 1, 0, -1}, yd[4] = {1, 0, -1, 0};
       vector<vector<int>> matrix(n, vector<int>(n));
       int x = 0, y = 0, d = 0;
       for (int i = 1; i <= n * n; i ++) {
           matrix[x][y] = i;
           int a = x + xd[d], b = y + yd[d];
           if (a < 0 || b < 0 || a >= n || b >= n || matrix[a][b]) {
               d = (d + 1) % 4;
               a = x + xd[d], b = y + yd[d]; 
           }
           x = a, y = b;
       }
       return matrix;
    }
};

（模拟）

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        int t = 0, r = n - 1, b = n - 1, l = 0;
        vector<vector<int>> ans(n, vector<int>(n));
        int num = 1;
        while (num <= n * n) {
            for (int i = l; i <= r; i ++) ans[t][i] = num ++;
            t ++;
            for (int i = t; i <= b; i ++) ans[i][r] = num ++;
            r --;
            for (int i = r; i >= l; i --) ans[b][i] = num ++;
            b --;
            for (int i = b; i >= t; i --) ans[i][l] = num ++;
            l ++;
        }
        return ans;
    }
};

29. 两数相除

（倍增）

和快速幂是一个思想，都是倍增的思想。倍增的思想就是将一个数字使用二进制表示的方式每一次都是成倍数的增加。

我们可以将divisor拆成二进制的形式。然后将小于dividend的所有divisor的倍数都保存起来，然后从大到小的从dividend扣除divisor的倍数，然后ans加上对应divisor的倍数即可。

class Solution {
public:
    typedef long long LL;
    int divide(int x, int y) {
        bool is_minus = false;
        if (x < 0 && y > 0 || x > 0 && y < 0) is_minus = true;
        vector<LL> nums;
        LL a = abs((LL)x);
        LL b = abs((LL)y);
        for (LL i = b; i <= a; i += i) nums.push_back(i);
        LL ans = 0;
        for (int i = nums.size() - 1; i >= 0; i --) {
            if (a >= nums[i]) {
                a -= nums[i];
                ans += 1ll << i;
            }
        }
        if (!is_minus && ans > INT_MAX || ans < INT_MIN) return INT_MAX;
        if (!is_minus) return ans;
        else return -ans;
    }
};

（倍增2-试减法）

也可以不用将divisor的倍数都保存起来，可以一边比较dividend中剩余的数值，一边从dividend中去除divisor在dividend的最高倍数。也就是将divisor的二进制从最大到最小的计算出来。

class Solution {
public:
    typedef long long LL;
    int divide(int dividend, int divisor) {
        if (dividend == INT_MIN && divisor == -1) return INT_MAX;
        LL x = dividend, y = divisor;
        bool is_minus = false;
        if ((x < 0 && y > 0) || (x > 0 && y < 0)) is_minus = true;
        if (x < 0) x *= -1;
        if (y < 0) y *= -1;

        LL ans = 0;
        while (x >= y) {
            LL cnt = 1;
            LL t = y;
            while (t + t <= x) {
                cnt += cnt;
                t += t;
            }
            ans += cnt;
            x -= t;
        }
        if (is_minus) ans *= -1;
        if (ans < INT_MIN || ans > INT_MAX) return INT_MAX;
        return ans;
    }
};

（倍增+二分）

我们也可以发现，如果说x/y = k的话，那么[1, k]使得y*k <= x，[k+1, ...]使得y*k > x。所以这一段的数字具有了二段性。因此我们可以找到最后一个可以使得y*k <= x的k即可。

因为中间不能使用乘除法，所以我们也可以利用上面同样的倍增的思想，利用位运算计算出a*b的大小即可。

class Solution {
public:
    typedef long long LL;
    LL mul(LL a, LL b) {
        LL ans = 0;
        while (b) {
            if (b & 1) ans += a;
            b >>= 1;
            a += a;
        }
        return ans;
    }

    int divide(int a, int b) {
        // 特判a=INT_MIN,b=1的情况
        if (a == INT_MIN && b == 1) return a;
        LL x = a, y = b;
        bool is_minus = false;
        if ((x > 0 && y < 0) || (x < 0 && y > 0)) is_minus = true;
        if (x < 0) x *= -1;
        if (y < 0) y *= -1;
        LL l = 0, r = x;
        while (l < r) {
            LL mid = l + (r - l + 1) / 2;
            if (mul(mid, y) <= x) l = mid;
            else r = mid - 1;
        }
        if (l > INT_MAX || l < INT_MIN) return INT_MAX;
        if (is_minus) l *= -1;
        return l;
    }
    
};

（使用int的倍增法）

如果题目中要求只能使用int类型的变量的话，因为INT_MIN的绝对值要比INT_MAX多一，所以我们可以将所以的数字都变成负数，这样的话所以的数字至少都可以储存起来了，只是计算的逻辑刚好反过来了而已。

class Solution {
public:
    int divide(int x, int y) {
        // 防止x==INT_MIN的情况
        // 1.INT_MIN*-1比INT_MAX还要大
        if (x == INT_MIN && y == -1) return INT_MAX;
        // 2.INT_MIN*1之后的正数比INT_MAX还要大
        if (y == 1) return x; 
        
        bool is_minus = false;
        if ((x < 0 && y > 0) || (x > 0 && y < 0)) is_minus = true;
        if (x > 0) x *= -1;
        if (y > 0) y *= -1;
        int ans = 0;
        while (y >= x) {
            int cnt = 1;
            int t = y;
            while (t >= x - t) {
                t += t;
                cnt += cnt;
            } 
            ans += cnt;
            x -= t;
        }
        if (is_minus) ans *= -1;
        return ans; 
    }
};

总结：倍增的思想用于一个数的幂或者两个数字的快速相乘或者相除。本质都是将其中一个数字使用而二进制的方式表示出来，来达到快速计算的效果。

207. 课程表

（拓扑排序+bfs）

一个图不存在环等价于这个图的反向图不存在环。

本题是一个考察图论的题目，关键在于判断图中是否存在环（判断拓扑排序）。

拓扑排序四步走：

1.使用邻接表将这个图存储下来

2.找到度为0的定点，加入在队列中

3.bfs，减少点的入度，并将入读为0的定点加入到队列中

4.判断是否存在顶点存在入度，如果存在说明图中有环，因此没有拓扑序直接返回false

class Solution {
public:
    bool canFinish(int n, vector<vector<int>>& edges) {
        vector<vector<int>> g(n);
        vector<int> count(n);
        for (auto& edge : edges) {
            int a = edge[1], b = edge[0];
            g[a].push_back(b);
            count[b] ++;
        }
        
        queue<int> q;
        for (int i = 0; i < n; i ++)
            if (!count[i])
                q.push(i);
        
        int cnt = 0;
        while (!q.empty()) {
            int top = q.front();
            q.pop();
            cnt ++;
            int len = g[top].size();
            for (int i = 0; i < len; i ++) {
                count[g[top][i]] --;
                if (!count[g[top][i]])
                    q.push(g[top][i]);
            }
        }
        return n == cnt;
    }
};

（拓扑排序+dfs）

前面使用广度优先搜索时从正面的角度去理解一个图是否存在环，因为我们是在考虑一个课程前面是否还存在先修课程，对应到图中，也就是一个图中的某一个顶点是否存在入度，如果不存在入度的话，那么这个课程就可以开始学习了。

但是如果是深度优先遍历的话，我们就题目转化为一个图是否存在环？

我们从一个顶点出发的话，这个顶点可能前面有先修的课程，也有可能这个课程已经是入度为0的点了。这时我们只需要顺着这个顶点一直往前找到：**以这个顶点为出发点的终点是哪一个顶点。**在这之前我们就需要使用一个flags数组标记一下每一个位置的访问情况，flags[i] = 0表示没有访问过该节点，flags[i] = 1表示这个节点在本轮dfs中访问过，flags[i] = -1表示这个点已经被访问过了。如果一个图中存在环的话，那么一定会有重复访问flags[i] = 1的位置，这样就直接return false即可。

class Solution {
public:
    bool dfs(int index, vector<vector<int>>& g, vector<int>& flags) {
        if (flags[index] == -1) return true; // 这个点已经被其他点访问过了，可以直接退出
        if (flags[index] == 1) return false; // 在同一轮dfs中找到一个点两次，说明有环
        flags[index] = 1;
        for (auto v : g[index]) {
            if (!dfs(v, g, flags))
                return false;
        }
        flags[index] = -1;
        return true;
    }

    bool canFinish(int n, vector<vector<int>>& edges) {
        vector<vector<int>> g(n);
        vector<int> flags(n);
        for (auto& edge : edges) {
            int cur = edge[0], pre = edge[1];
            g[pre].push_back(cur); // pre->cur
        }
        
        for (int i = 0; i < n; i ++) {
            if (!dfs(i, g, flags))
                return false;
        }
        return true;
    }
};

673. 最长递增子序列的个数

（动规-进阶版LIS）

我们都知道最简单的LIS问题，即最长上升子序列问题。LIS问题的朴素版本就是利用动规递推出以i结尾的最长上升子序列的长度。但是本题需要求出最长上升子序列的个数。所以我们就可以在使用一个数组g[i]表示以i结尾的最长上升子序列的个数。最后总的求出最长上升子序列的个数。

总体思路：

1、求出以i结尾的最长上升子序列的长度

2、求出以i结尾的最长上升子序列的个数，即if (dp[j] + 1 > dp[i])的话，更新dp[i] = dp[j] + 1的同时也需要更新count[i] = count[j]。if(dp[j] + 1 == dp[i])的话，累计以i为结尾的LIS的个数，即count[i] += count[j]。

3、计算出LIS的长度，统计dp[i] == len(LIS)中，ans += count[i]。

class Solution {
public:
    int findNumberOfLIS(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n, 1), count(n, 1);
        int maxLen = 0;
        for (int i = 0; i < n; i ++) {
            for (int j = 0; j < i; j ++) {
                if (nums[i] > nums[j]) {
                    if (dp[j] + 1 > dp[i]) { // 如果长度更新了，说明LIS个数需要更新
                        count[i] = count[j];
                        dp[i] = dp[j] + 1;
                    } else if (dp[j] + 1 == dp[i]) { //如果出现了重复的LIS，就相加两个LIS
                        count[i] += count[j];
                    }
                }
            }
            maxLen = max(maxLen, dp[i]);
        }
        int ans = 0;
        for (int i = 0; i < n; i ++)
            if (dp[i] == maxLen)
                ans += count[i];
        return ans;
    }
};

223. 矩形面积

（数学）

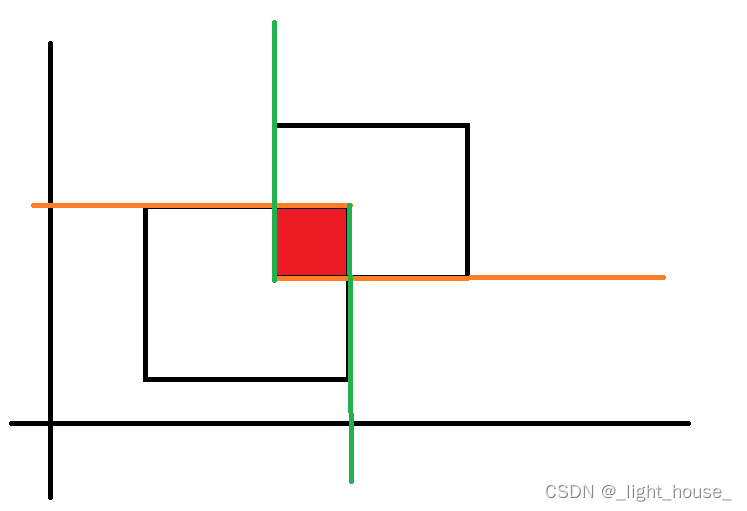
我们要计算一个矩形的股改面积，就是在求出面积A + 面积B - (面积A和面积B的交集)，关键就是求出两个矩形的交集。

我们先来搞清楚一维的交集是怎么求的。

而矩形的交集面积就是两个一维的线段构成的面积

class Solution {
public:
    int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
        int lx = max(ax1, bx1), ly = max(ay1, by1);
        int rx = min(ax2, bx2), ry = min(ay2, by2);
        int intersection = max(0, (rx - lx)) * max(0, (ry - ly));
        int sum = (ay2 - ay1) * (ax2 - ax1) + (by2 - by1) * (bx2 - bx1);
        return sum - intersection;
    }
};

（数学2）

class Solution {
public:
    int computeArea(int ax1, int ay1, int ax2, int ay2, int bx1, int by1, int bx2, int by2) {
        int X = max(0, min(ay2, by2) - max(ay1, by1));
        int Y = max(0, min(ax2, bx2) - max(ax1, bx1));
        int sum = (ax2 - ax1) * (ay2 - ay1) + (bx2 - bx1) * (by2 - by1);
        return sum - X * Y;
    }
};

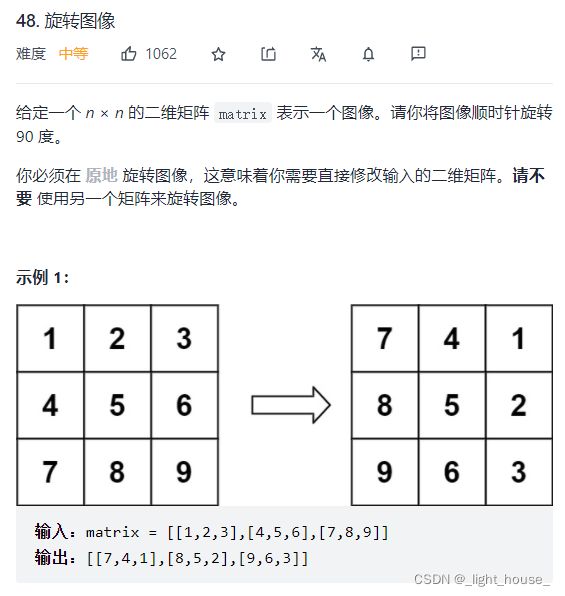
48. 旋转图像

（找规律）

第一种方法就是将每四个元素分成一组，并将四个元素在组内两两交换，然后进行下一组的交换。这个方法比较麻烦。

组内的四个元素的反转满足的规律：反转前的坐标：(x, y)，反转后的坐标：(y, n - 1 - x)

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        int t = 1;
        int cnt = n;
        for (int i = 0; i < n / 2; i ++) {
            for (int x = i, y = i; y < i + cnt - 1; y ++) {
                int num = matrix[x][y];
                int tx = y, ty = n - x - 1;
                for (int k = 0; k < 4; k ++) {
                    int tmp = matrix[tx][ty];
                    matrix[tx][ty] = num;
                    num = tmp;
                    int a = tx, b = ty;
                    tx = b;
                    ty = n - a - 1;
                }
            }
            t *= 2;
            cnt -= 2;
        }
    }
};

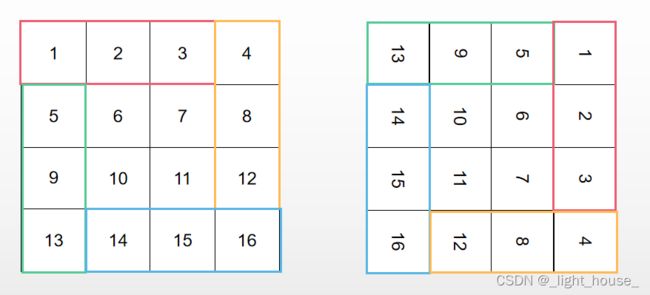
（找规律2）

如果想顺时针反转90°的话，可以像反转-180°，然后再反转270°。

反转-180°就是将数组上下反转，反转270°就是将数组沿着正对角线对称反转。

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        // 反转-180度
        for (int t = 0, b = n - 1; t < b; t ++, b --) {
            for (int i = 0; i < n; i ++) {
                swap(matrix[t][i], matrix[b][i]);
            }
        }
        // 反转270度
        for (int i = 0; i < n; i ++) {
            for (int j = i + 1; j < n; j ++) {
                swap(matrix[i][j], matrix[j][i]);
            }
        }
    }
};

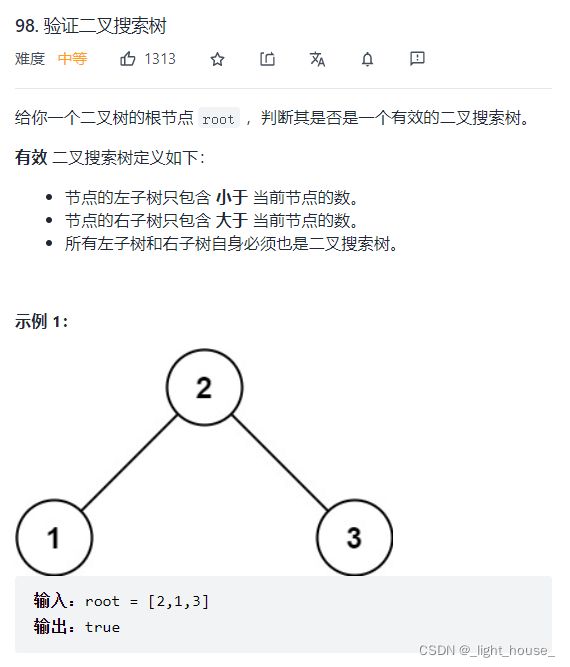
98. 验证二叉搜索树

（递归）

验证二叉搜索树的方法有很多，我们可以根据二叉搜索树的特点倒退出它的验证方法。

因为二叉搜索树的root的值一定大于左子树中所有节点的值，而也一定小于右子树中所有节点的值。所以更具这一点我们就可以判断二叉搜索树的平衡性。

class Solution {
public:
    typedef long long LL;
    const LL INF = LONG_MAX;
    LL Min(TreeNode* root) {
        if (!root) return INF;
        if (!root->left && !root->right) return root->val;
        return fmin(root->val, fmin(Min(root->left), Min(root->right)));
    }

    LL Max(TreeNode* root) {
        if (!root) return -INF;
        if (!root->left && !root->right) return root->val;
        return fmax(root->val, fmax(Max(root->left), Max(root->right)));
    }

    bool isValidBST(TreeNode* root) {
        if (!root) return true;
        if (!root->left && !root->right) return true;
        LL left = Max(root->left);
        LL right = Min(root->right);
        if (root->val < right && root->val > left) {
            return isValidBST(root->left) && isValidBST(root->right);
        } else {
            return false;
        }
    }
};

（中序遍历）

因为搜索树的中序遍历一定是有序的，所以我们可以直接根据其中序遍历是否有序来判断是否为二叉搜索树。

class Solution {
public:
    long prev = LONG_MIN;
    bool isValidBST(TreeNode* root) {
        if (!root) return true;
        // 判断左子树
        if (!isValidBST(root->left)) return false;
        // 判断根节点
        if (root->val <= prev) return false;
        prev = root->val;
        // 判断右子树
        if (!isValidBST(root->right)) return false;
        return true;
    }
};

1488. 避免洪水泛滥

（贪心+二分）

本题如果会洪水泛滥的话，情况如下：

• 连续的下雨，不能及时的将雨水处理掉。

对这种情况的话，我们可以记录下一个地方下雨的时间，当一个地方的湖泊即将要洪水泛滥的时候，我们判断是否在此之前可以有rains[i] == 0的时候，可以将当前这个洪水泛滥的地方的雨水处理掉。注意：处理一个地方的雨水的前提是这个地方已经有雨水了，如果是[0, 1, 1]这样的话，虽然有处理雨水的机会，但是是在这个地方下雨之前，那么这次雨水处理的机会其实就没有用了。

一个地方下雨的时间可以使用unordered_map记录，所以关键在于记录处理雨水的时间。我们可以使用一个set来记录，因为我们需要快速的找到可以处理雨水的时间，而set中的元素本身是有序的，所以我们可以在set记录下雨的时间，然后通过二分找到快速的判断是否能在一个地方洪水泛滥前处理掉洪水。

class Solution {
public:
    vector<int> avoidFlood(vector<int>& rains) {
        int n = rains.size();
        vector<int> ans(n, 1);
        unordered_map<int, int> rainDay;
        set<int> zero;
        for (int i = 0; i < n; i ++) {
            if (rains[i] == 0) {
                zero.insert(i);
            } else {
                if (rainDay.count(rains[i])) {
                    auto it = zero.lower_bound(rainDay[rains[i]]);
                    if (it == zero.end()) return {};
                    ans[*it] = rains[i];
                    zero.erase(it);
                }
                rainDay[rains[i]] = i;
                ans[i] = -1;
            }
        }
        return ans;
    }
};

470. 用 Rand7() 实现 Rand10()

（数学）

(rand_X() - 1) * Y + rand_Y = rand_XY

rand_Y = rand_X % Y + 1

class Solution {
public:
    int rand10() {
        int t = (rand7() - 1) * 7 + rand7();
        if (t > 40) return rand10();
        return t % 10 + 1;
    }
};

134. 加油站

（贪心+数组）

我们如果想要使用暴力解法的话，就可以两层循环，先枚举所有的起点，然后再枚举走的路程。中间如果剩余的油量小于零的话，那么就可以提前退出了。

我们可以基于暴力解法写一个优化的版本。我们要知道如果[i, ....., j]这一段是从i位置出发，到达j位置的时候剩余的油量就不够了。那么在[i, j]中间选一个位置k，其实也不能到达j位置。因为从i出发到达k位置的话，此时的剩余油量>= 0，也到不了j位置。那么从k位置出发，此时的剩余油量为0，那么就更不可能到达j位置了。

因此如果从i位置出发到不了j位置的话，那么就可以不用枚举[i, j]中的位置作为起点出发了，而是从j + 1位置出发判断是否可以绕一圈。

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int n = gas.length;
        int i = 0;
        while (i < n) {
            int sum = 0, j = 0;
            while (j < n) {
                int k = (i + j) % n;
                sum += gas[k] - cost[k];
                if (sum < 0) break;
                j ++;
            }
            if (j == n) return i;
            else i = i + j + 1;
        }
        return -1;
    }
}

678. 有效的括号字符串

（动规）

class Solution {
public:
    bool checkValidString(string s) {
        int n = s.size();
        vector<vector<bool>> f(n + 1, vector<bool>(n + 1));
        f[0][0] = true;
        for (int i = 1; i <= n; i ++) {
            for (int j = 0; j <= i; j ++) {
                if (s[i - 1] == '(') {
                    if (j - 1 >= 0) f[i][j] = f[i - 1][j - 1];
                } else if (s[i - 1] == ')') {
                     if (j + 1 <= i) f[i][j] = f[i - 1][j + 1];
                } else {
                    f[i][j] = f[i - 1][j];
                    if (j + 1 <= i) f[i][j] = f[i][j] || f[i - 1][j + 1];
                    if (j - 1 >= 0) f[i][j] = f[i][j] || f[i - 1][j - 1];
                }
            }
        }
        return f[n][0];
    }
};

（贪心）

我们知道判断括号是否合法有两个条件：

1、字符串中左括号和右括号的数量相同。

2、任意一段前缀中左括号的数量大于等于右括号的数量。

所以一般判断字符串是否合法可以通过中间右括号的数量是否小于零来筛选掉不合法的方案，最后判断左括号的数量是否为0。

但是本题中除了左右括号之外还有*。所以我们此时的判断左括号的数量就不能用一个数字来判断了。而是使用一个范围来判断左括号的数量。

如果s[i]=='('，则l ++, r ++。

如果s[i] == ‘)’，则l --, r --。

如果s[i == '*'，则l --, r ++。

并且因为字符串中左括号的范围最少一定是>=0的，所以每一次都需要将l = max(l, 0)一下。

最后也是判断使用最少的左括号是否可以为0，即判断l == 0。如果l == 0，说明可以字符串中的左括号刚好可以抵消掉字符串中的右括号，并且没有冗余的左括号。

class Solution {
public:
    bool checkValidString(string s) {
        int n = s.size();
        int l = 0, r = 0;
        for (int i = 0; i < n; i ++) {
            if (s[i] == '(') l ++, r ++;
            else if (s[i] == ')') l --, r --;
            else if (s[i] == '*') l --, r ++;
            l = max(l, 0);
            if (r < 0) return false;
        }
        return l == 0;
    }
};

227. 基本计算器 II

（栈）

本题是一个表达式求值的题目，对于表达式求值的题目而言，我们通常可以套用一个模板，即考虑字符串中的字符的分类：

1、如果s[i] == ‘ ’的话，那么可以直接跳过。

2、如果isdigit(s[i])的话，那么我们就需要使用双指针将一个数字从字符串中抠出来。

3、如果s[i] == '('的话，直接压入存放操作符的栈中。

4、如果s[i] == ‘)’的话，就将操作符栈中的表达式计算一遍，直到遇到‘(’。

5、如果s[i]是运算符的话，我们需要给运算符一个优先级，如果操作符的栈中的栈顶元素的优先级要大于等于当前运算符的优先级的话，那么就将栈中的表达式先进行运算。为了表示运算符的优先级，我们需要使用一个哈希表存储一个运算符对应的优先级。

6、字符串中出现负数或者特殊字符，类似-1 + (-1)这样的表达式。我们需要在运算符的前面加上一个0，这样计算才不会报错。（而且因为需要判断s[i - 1]，所以我们需要先对字符串的空格过滤一下，否则( -1)这样的案例就过了了。

上述的是模板，但是本题目没有括号和负数。所以我们直接套用1,2,5,三点即可。

class Solution {
public:
    stack<int> nums;
    stack<char> op;

    void cal() {
        int b = nums.top(); nums.pop();
        int a = nums.top(); nums.pop();
        char ch = op.top(); op.pop();
        int ans = 0;
        if (ch == '+') ans = a + b;
        if (ch == '-') ans = a - b;
        if (ch == '*') ans = a * b;
        if (ch == '/') ans = a / b;
        nums.push(ans);
    }

    int calculate(string s) {
        int n = s.size();
        unordered_map<char, int> pr;
        pr['+'] = pr['-'] = 0;
        pr['*'] = pr['/'] = 1;
        for (int i = 0; i < n; i ++) {
            if (s[i] == ' ') continue;
            else if (isdigit(s[i])) {
                int num = 0, j = i;
                while (j < n && isdigit(s[j])) {
                    num = num * 10 + (s[j] - '0');
                    j ++;
                }
                i = j - 1;
                nums.push(num);
            } else {
                while (!op.empty() && pr[op.top()] >= pr[s[i]]) cal();
                op.push(s[i]);
            }
        }
        while (!op.empty()) cal();
        return nums.top();
    }
};

224. 基本计算器

（栈）

本题有没有乘除元素，但是有空格，有括号，有负数。所以直接套用整个表达式模板即可。

1、如果s[i] == ‘ ’的话，那么可以直接跳过。

2、如果isdigit(s[i])的话，那么我们就需要使用双指针将一个数字从字符串中抠出来。

3、如果s[i] == '('的话，直接压入存放操作符的栈中。

4、如果s[i] == ‘)’的话，就将操作符栈中的表达式计算一遍，直到遇到‘(’。

5、如果s[i]是运算符的话，我们需要给运算符一个优先级，如果操作符的栈中的栈顶元素的优先级要大于等于当前运算符的优先级的话，那么就将栈中的表达式先进行运算。为了表示运算符的优先级，我们需要使用一个哈希表存储一个运算符对应的优先级。

6、字符串中出现负数或者特殊字符，类似-1 + (-1)这样的表达式。我们需要在运算符的前面加上一个0，这样计算才不会报错。（而且因为需要判断s[i - 1]，所以我们需要先对字符串的空格过滤一下，否则( -1)这样的案例就过了了。

class Solution {
public:
    stack<int> nums;
    stack<char> op;

    void cal() {
        int b = nums.top(); nums.pop();
        int a = nums.top(); nums.pop();
        char ch = op.top(); op.pop();
        int ans = 0;
        if (ch == '+') ans = a + b;
        if (ch == '-') ans = a - b;
        nums.push(ans);
    }

    int calculate(string rs) {
        string s;
        for (char c : rs) 
            if (c != ' ')
                s += c;
        unordered_map<char, int> pr;
        pr['+'] = pr['-'] = 0;
        pr['('] = pr[')'] = -1; // 因为需要特殊处理(),所以()的优先级设置成最低即可
        int n = s.size();
        for (int i = 0; i < n; i ++) {
            if (s[i] == '(') op.push(s[i]);
            else if (isdigit(s[i])) {
                int num = 0, j = i;
                while (j < n && isdigit(s[j])) {
                    num = num * 10 + (s[j] - '0');
                    j ++;
                }
                i = j - 1;
                nums.push(num);
            } else if (s[i] == ')') {
                while (op.top() != '(') cal();
                op.pop();
            } else {
                // 处理负数和特殊符号
                if (!i || s[i - 1] == '(' || s[i - 1] == '-' || s[i - 1] == '+')
                    nums.push(0);
                while (!op.empty() && pr[op.top()] >= pr[s[i]]) cal();
                op.push(s[i]);
            }
        } 
        while (!op.empty()) cal();
        return nums.top();
    }
};

187. 重复的DNA序列

（哈希表）

本题就是需要求出出现次数超过1次的长度为10的字符串。所以我们就可以使用一个哈希表将所有的字符串长度为10的字符串放入哈希表中，统计一下次数。如果出现次数>= 2的字符串就可以直接放入答案中。

class Solution {
public:
    vector<string> findRepeatedDnaSequences(string s) {
        unordered_map<string, int> hash;
        int n = s.size();
        vector<string> ans;
        for (int i = 0; i + 10 <= n; i ++) {
            string tmp = s.substr(i, 10);
            // 注意：不能重复放入相同的字符串所以只有等于2的时候可以放入
            if (++ hash[tmp] == 2) { 
                ans.push_back(tmp); 
            }
        }
        return ans;
    }
};

（字符串哈希）

但是作为本题的优化，因为字符串被放入哈希表中存放和查找的效率都和字符串的长度有关。因为本题中已经说了查找的字符串的长度一定为10，所以就算是直接放入哈希表效率的下降也就是系数级别增大的（O(10N)。但是如果下次字符串长度不确定的话，就需要将字符串转化为一个整数放入哈希表中，这样就可以降低哈希表查找的效率了。

class Solution {
public:
    const int P = 131; // 或者13131也可以
    typedef unsigned long long ULL;
    vector<string> findRepeatedDnaSequences(string s) {
        int n = s.size();
        vector<string> ans;
        unordered_map<ULL, int> hash;
        for (int i = 0; i <= n - 10; i ++) {
            ULL num = 0;
            for (int j = i; j < i + 10; j ++) {
                num = num * P + s[j];
            }
            hash[num] ++;
            if (hash[num] == 2) {
                ans.push_back(s.substr(i, 10));
            }
        }
        return ans;
    }
};

（哈希表+位运算）

上面的方法虽然使得哈希表的插入和查询的时间效率增加了，但是字符串哈希还是在循环的内部进行的，因此总体的时间复杂度还是10N的。

如果我们需要进一步的降低的话，要么我们可以预处理字符串哈希，可以将字符串转化为整数之后形成前缀和数组这样就可以使用O(1)的时间找到一段长10的字符串。

还有另一种方案就是可以使用滑动窗口的方式，就可以不用来回的扫描长为10的字符串，就可以做到O(N)的时间复杂度。

我们转换一下哈希的方式，我们不将字符串转化为一个整数，而是将字符串使用位运算表示出来。因为字符串中只有4种字符，也就可以映射成00,01,10,11四种状态。而一个长10的字符串就可以使用20个位来表示，我们就可以使用32位的int来标识一个字符串。

1、字符从右边进入窗口，x << 2 | bin[s[i]]

2、字符从左边的窗口退出，x & ((1 << 20) - 1)，即x & 0000 0000 0000 1111 1111 1111 1111 1111，这样就可以只保留int整数的后20位。

class Solution {
public:
    unordered_map<char, int> bin = {
        {'A', 0}, {'C', 1}, {'G', 2}, {'T', 3},
    };
    vector<string> findRepeatedDnaSequences(string s) {
        int n = s.size();
        int x = 0;
        // 预处理前9个字符，使其先进入窗口中
        for (int i = 0; i < 9; i ++) {
            x = x << 2;
            x = x | bin[s[i]];
        }
        unordered_map<int, int> hash;
        vector<string> ans;
        for (int i = 0; i + 10 <= n; i ++) {
            x = ((x << 2) | bin[s[i + 9]]) & ((1 << 20) - 1);
            if (hash[x] == 1) ans.push_back(s.substr(i, 10));
            hash[x] ++;
        }
        return ans;
    }
};

class Solution {
public:
    unordered_map<char, int> bin = {
        {'A', 0}, {'C', 1}, {'G', 2}, {'T', 3},
    };
    vector<string> findRepeatedDnaSequences(string s) {
        int n = s.size();
        int x = 0;
        unordered_map<int, int> hash;
        vector<string> ans;
        for (int i = 0; i < n; i ++) {
            x = ((x << 2) | bin[s[i]]) & ((1 << 20) - 1);
            if (i >= 9) {
                if (hash[x] == 1) ans.push_back(s.substr(i - 9, 10));
                hash[x] ++;
            }
        }
        return ans;
    }
};

总结：本题考的是哈希的映射。

我们使用字符串哈希可以有两种：第一种就是将一个字符串转化成一个P(13131)进制的数字，第二种就是将一个字符串的每一位用四种状态来表示，最后将一个字符串转化一个int类型的数字。

而如果想要降低时间复杂度的话，我们可以前缀和或者滑动窗口的思想，使得时间复杂度为O(N)。这两种方法都是可以使用O(N)的时间快速地定位一段区间中的字符。

698. 划分为k个相等的子集

（递归回溯）

class Solution {
public:

    bool dfs(vector<int>& nums, int index, vector<bool>& vis, int target) {
        int n = nums.size();

        if (target < 0) return false;
        if (target == 0) return true;
        if (n == index) return false;

        for (int i = index; i < n; i ++) {
            if (vis[i]) continue;
            vis[i] = true;
            if (dfs(nums, i + 1, vis, target - nums[i])) return true;
            vis[i] = false;
        }
        return false;
    }

   bool canPartitionKSubsets(vector<int>& nums, int k) {
        int n = nums.size();
        int sum = 0;
        for (int num : nums) sum += num;
        if (sum % k != 0) return false;
        int target = sum / k;
        sort(nums.begin(), nums.end(), greater<int>());
        vector<bool> vis(n);
        for (int i = 0; i < n; i ++) {
            if (dfs(nums, 0, vis, target)) k --;
        }
        return k == 0;
    }
};

（递归回溯+四种剪枝）

1、从大到小排序，这样剪枝可以更快

2、如果nums[i]开头组合失败，同时nums[i] == nums[i + 1]的话，那么nums[i + 1]开头也会失败。

3、如果nums[i]是一组数的开头并且组合失败的话，那么数组中一定不能组合成k个等和子集。

4、如果nums[i]是一组数的最后一个数并且组合失败了，那么数组中一定不能组合成k个等和子集。

class Solution {
public:
    vector<bool> vis;
    int target;

    bool dfs(vector<int>& nums, int start, int cur, int k) {
        if (!k) return true;
        if (cur == target) return dfs(nums, 0, 0, k - 1);

        int n = nums.size();
        for (int i = start; i < n; i ++) {
            if (vis[i]) continue;
            if (cur + nums[i] <= target) {
                vis[i] = true;
                if (dfs(nums, i + 1, cur + nums[i], k)) return true;
                vis[i] = false;
            }
            while (i + 1 < n && nums[i] == nums[i + 1]) i ++; // 剪枝3
            if (!cur || cur + nums[i] == target) return false; // 剪枝4,5
        }
        return false;
    }
    
    bool canPartitionKSubsets(vector<int>& nums, int k) {
        int n = nums.size();
        vis.resize(n);
        int sum = accumulate(nums.begin(), nums.end(), 0); 
        if (sum % k != 0) return false; // 剪枝1
        target = sum / k;
        sort(nums.begin(), nums.end(), greater<int>()); //剪枝2
        return dfs(nums, 0, 0, k);
    }
};

1838. 最高频元素的频数

（排序+滑动窗口）

我们要计算出高频数出现的最大频数。简单来说题目的要求就是要让我们使用k次加法使得数组中的一个数字出现的尽可能的多。

我们需要做的就是将k分配给数组中的数字。如果分配，哪个数字才是高频数字，这就是我们需要解决的问题。

本题的核心思想就是将一段区间中的数字都变成高频数字，而每一个数字都可能成为高频数字，所以我们可以枚举所有的数字当做高频数字，然后使得一段区间中的数字都变成高频数字同时判断变化的次数和k的大小即可。而维护一段区间的任务我们使用滑动窗口来解决。

class Solution {
public:
    typedef long long LL;
    int maxFrequency(vector<int>& nums, int k) {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        int ans = 1;
        LL cnt = 0;
        // 因为可能(nums[r] - nums[r - 1]) * (r - l)会爆int范围
        LL l = 0, r = 1;
        // 以nums[r]为基准，即把nums[r]当做出现频率最高的数字
        // 让一段区间中的所有数字调节成nums[r],判断所需的次数和k的大小
        while (r < n) {
            cnt += (nums[r] - nums[r - 1]) * (r - l);
            while (cnt > k) { 
                cnt -= nums[r] - nums[l];
                l ++;
            }
            ans = max(ans, r - l + 1);
            r ++;
        }
        return ans;
    }
};

（二分+前缀和）

上面说了本题的核心思想就是枚举所有的数字都当做是高频数字，然后所有的让其他数字向高频数字看齐。

而我们要做的就是用k次变换将其他数字尽可能多的变成高频数字。

滑动窗口可以使得我们将每一次的变化的次数记录下来，然后通过窗口的伸缩来调节。而如果我们想要快速的知道变化的差值的话，也可以通过前缀和的方式知道和nums[i]高频数字的差值。然后通过二分快速的查到与nums[i]平齐的下限即可。

class Solution {
public:
    typedef long long LL;
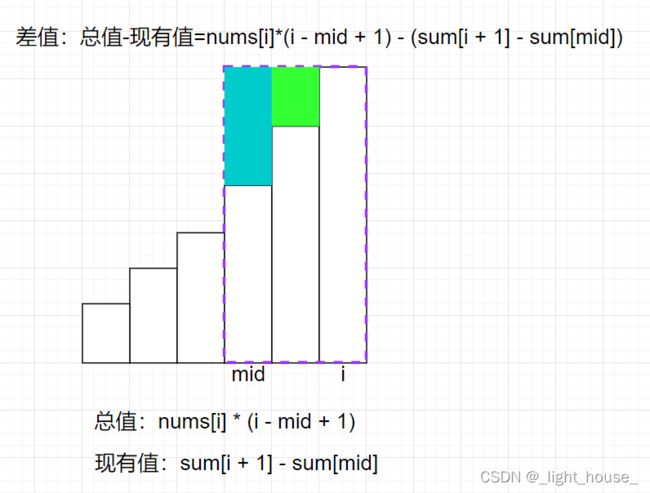
    bool check(vector<int>& nums, vector<LL>& sum, int mid, int i, int k) {
        LL t = (LL)nums[i] * (LL)(i - mid + 1) - (LL)(sum[i + 1] - sum[mid]); 
        return t <= k;
    }

    int maxFrequency(vector<int>& nums, int k) {
        int n = nums.size();
        sort(nums.begin(), nums.end());
        vector<LL> sum(n + 1);
        for (int i = 1; i <= n; i ++) 
            sum[i] = sum[i - 1] + nums[i - 1];
        int ans = 0;
        for (int i = 0; i < n; i ++) {
            int l = 0, r = i;
            while (l < r) {
                int mid = (l + r) / 2;
                if (check(nums, sum, mid, i, k)) r = mid;
                else l = mid + 1;
            }
            ans = max(ans, i - l + 1);
        }
        return ans;
    }
};

138. 复制带随机指针的链表

（哈希表）

本题需要我们深拷贝一个有随件指针的链表，而本题的难点就在于找到每一个节点随机指针指向的节点。

因为每一个节点的值有可能会重复，所以我们不能通过循环整个链表找到与node->val相等的节点作为随机指针指向的节点。

所以我们可以使用哈希表将一个节点和它的复制节点建立一个映射关系。当我们在对应两个节点的时候，我们就可以通过hash[cur]->next = hash[cur->next], hash[cur]->random = hash[cur->random]的方式建立映射关系。

class Solution {
public:
    Node* copyRandomList(Node* head) {
        unordered_map<Node*, Node*> hash;
        for (auto cur = head; cur; cur = cur->next) {
            Node* newNode = new Node(cur->val);
            hash[cur] = newNode;
        }
        for (auto cur = head; cur; cur = cur->next) {
            hash[cur]->next = hash[cur->next];
            hash[cur]->random = hash[cur->random];
        }
        return hash[head];
    }
};

（回溯+哈希表）

我们也可以通过递归回溯的方式建立映射关系。我们以深拷贝一个普通链表为基础，在递归函数中建立node和clone的映射关系，即hash[node] = clone。这样如果找clone->random的话，我们也可以通过clone->random = dfs(node->random)的方式建立映射关系，因为if (hash.count(nde)) return hash[node]。

class Solution {
public:
    unordered_map<Node*, Node*> hash;
    Node* dfs(Node* node) {
        if (!node) return nullptr;
        if (hash.count(node)) return hash[node];
        Node* clone = new Node(node->val);
        hash[node] = clone;
        clone->next = dfs(node->next);
        clone->random = dfs(node->random);
        return clone;
    }

    Node* copyRandomList(Node* head) {
        if (!head) return nullptr;
        return dfs(head); 
    }
};

（链表）

本题因为是链表的复制，所以链表本身的线性结构可以帮助我们不使用哈希表也可以快速的找到映射的节点。如果我们在每一个节点的后面接上它复制的节点。这样如果我们要映射一个节点的话，这个节点的下一个位置就是它的映射节点。

class Solution {
public:
    Node* copyRandomList(Node* head) {
        if (!head) return nullptr;
        Node* cur = head;
        while (cur) {
            Node* newNode = new Node(cur->val);
            newNode->next = cur->next;
            cur->next = newNode;
            cur = newNode->next;
        }
        cur = head;
        while (cur) {
            if (cur->random)
                cur->next->random = cur->random->next;
            cur = cur->next->next;
        }
        cur = head;
        Node* newHead = head->next;
        while (cur) {
            Node* nextNode = cur->next;
            cur->next = nextNode->next;
            if (nextNode->next)
                nextNode->next = nextNode->next->next;
            cur = cur->next;
        }
        return newHead;
    }
};

371. 两整数之和

（位运算）

因为不能使用+或者-，所以我们可以想到使用位运算去模拟这个过程。

这里有一个公式a ^ b = a+b的不进位的总和，(a & b) << 1 = a+b进位的总和。

所以我们就可以将a+b换成(a ^ b) + ((a & b) << 1)，并且因为(a & b) << 1每一次右边都会多出一个0，所以最多执行32次，就会使得这个int变成0。

注意：c++中需要将(a&b)转换成unsigned这样int类型溢出才不会报错。

class Solution {
public:
    int getSum(int a, int b) {
        while (b) {
            int x = a ^ b; // 不进位和
            int y = (unsigned)(a & b) << 1; // 进位和
            a = x;
            b = y;
        }
        return a;
    }
};

（位运算+递归）

class Solution {
public:
    int getSum(int a, int b) {
        if (!b) return a; 
        int x = a ^ b;
        int y = (unsigned)(a & b) << 1;
        return getSum(x, y);
    }
};

763. 划分字母区间

（贪心+哈希表+双指针）

我们可以将一个字符出现的范围表示为一段区间，而要求出的一段区间中只能存在一种字符意味着将这些区间合并成不重复的区间。

1、将所有的区间放进一个数组中。

2、贪心地将区间合并，即将区间的右端点尽量的往右拓展，如果出现一个区间的左端点比当前的右端点大的话，我们需要重新计算一段区间。

class Solution {
public:
    typedef pair<int, int> PII;
    vector<int> partitionLabels(string s) {
        vector<PII> segs;
        unordered_set<char> vis;
        int n = s.size();
        // 收集区间
        for (int i = 0; i < n; i ++) {
            if (vis.count(s[i])) continue;
            vis.insert(s[i]);
            for (int j = n - 1; j >= 0; j --) {
                if (s[j] == s[i]) {
                    segs.push_back({i, j});
                    break;
                }
            }
        }
        // 贪心合并区间
        vector<int> ans;
        int l = segs[0].first, r = segs[0].second;
        for (auto seg : segs) {
            if (seg.first > r) {
                ans.push_back(r - l + 1);
                l = seg.first;
                r = seg.second;
            } else {
                r = max(r, seg.second);
            }
        }
        ans.push_back(r - l + 1);
        return ans;
    }
};

（哈希表+贪心+双指针）

因为枚举区间是从前往后的，所以区间的开头一定是从小到大的。因此我们可以不用讲区间枚举出来，而是一边扩大区间，一边计算区间的右端点。

class Solution {
public:
    vector<int> partitionLabels(string s) {
        int n = s.size();
        vector<int> ans;
        unordered_set<char> hash;
        int l = 0, r = 0;
        for (int i = 0; i < n; i ++) {
            if (hash.count(s[i])) continue;
            if (i > r) {
                ans.push_back(r - l + 1);
                l = i;
            }
            for (int j = n - 1; j >= 0; j --) {
                if (s[j] == s[i]) {
                    r = max(r, j);
                    break;
                }
            }
        } 
        ans.push_back(r - l + 1);
        return ans;
    }
};

（哈希表+贪心）

在上面我们使用哈希表可以防止重复地计算相同字符的右端点。而我们也可以使用一个哈希表计算一个字符的右端点，而不是使用双指针。使用hash[s[i]] = i就可以不断地更新一个字符的最后一次出现的位置。而我们做的就是不断地更新区间的右端点，并且重新的开始一段新的区间。

class Solution {
public:
    vector<int> partitionLabels(string s) {
        int n = s.size();
        vector<int> ans;
        unordered_map<char, int> hash;
        for (int i = 0; i < n; i ++) hash[s[i]] = i;
        int l = 0, r = 0;
        for (int i = 0; i < n; i ++) {
            r = max(r, hash[s[i]]);
            if (i == r) {
                ans.push_back(r - l + 1);
                l = r = i + 1;
            }
        } 
        return ans;
    }
};

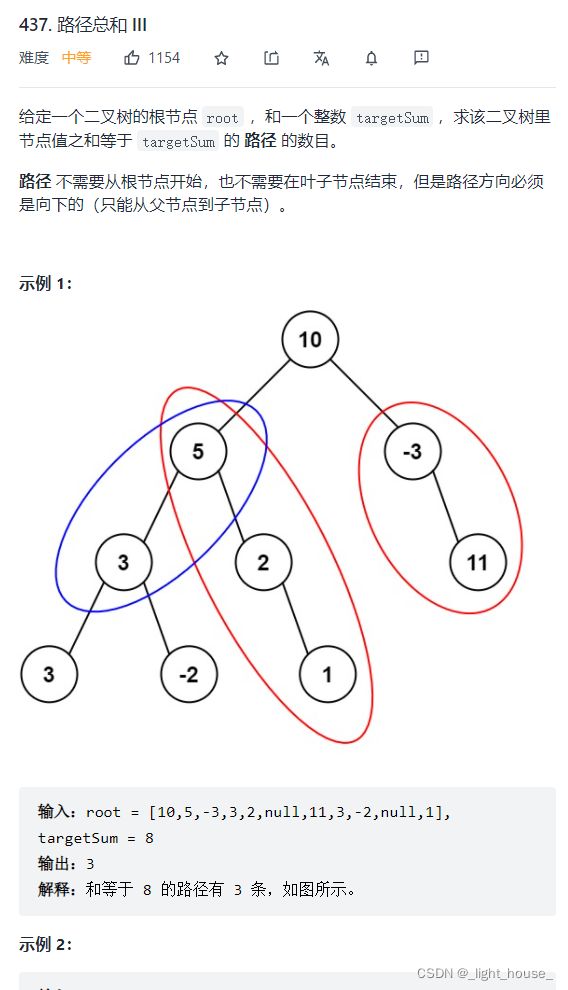
437. 路径总和 III

（递归）

第一种方法就是最暴力的方式。我们可以枚举所以节点作为根节点。然后以遍历到的节点作为根节点往下递归搜索是否存在路径和为sum的路径。如果有则ans ++。

class Solution {
    int ans = 0;
    public void dfs2(TreeNode root, int targetSum, int sum) {
        if (sum == targetSum) ans ++;
        if (root.left != null)
            dfs2(root.left, targetSum, sum + root.left.val);
        if (root.right != null)
            dfs2(root.right, targetSum, sum + root.right.val); 
    }

    public void dfs1(TreeNode root, int targetSum) {
        if (root == null) return ;
        dfs2(root, targetSum, root.val);
        dfs1(root.left, targetSum);
        dfs1(root.right, targetSum);
    }

    public int pathSum(TreeNode root, int targetSum) {
        helper(root, targetSum);
        return ans;
    }
}

（哈希表+前缀和+递归）

我们想要知道树上是否存在一个路径和是否等于target，其实如果将每一条树的分支看做是一段区间的话，我们就是想要快速地判断一段区间和是否等于target。

我们如果想要快速地知道一段区间的和可以使用前缀和的思想。但是我们知道了前缀和数组，需要使用sum[i] - sum[j] = target的方式才知道[j - 1, i]区间中的和，而如果需要枚举一段区间的左右两个端点的话，那么时间复杂度有变成$O(N^2)$了。

如果想要只用$O(N)$的时间就判断[0, i - 1]区间中是否存在区间和为target的区间的话，就可以将前缀和的公式变一下形，即s[j] = s[i] - target。也就是我们想要知道[0, i - 1]区间中是否存在一段区间和为target，只需要在[0, i - 1]中找到一个j使得s[j] = s[i] - target即可。

因此我们只需要在计算前缀和的时候，判断hash.containsKey(sum - target)即可。如果存在的话，就可以将hash.get(sum - target)加上。

注意：因为可能一条树的整个分支都是一个和为target的路径。所以我们需要将(0, 1)手动地添加到哈希表中，这样当枚举了路径上所有的节点时候，才可以有containsKey(0)这个选项。

class Solution {
    HashMap<Integer, Integer> hash = new HashMap<>();
    int ans = 0; 

    public void dfs(TreeNode root, int target, int sum) {
        if (root == null) return ;
        // 记录前缀和
        sum += root.val;
        // 查看是否包含s[j] = s[i] - target
        if (hash.containsKey(sum - target))
            ans += hash.get(sum - target);
        // 将前缀和放入哈希表中
        hash.put(sum, hash.getOrDefault(sum, 0) + 1);
        dfs(root.left, target, sum);
        dfs(root.right, target, sum);
        hash.put(sum, hash.getOrDefault(sum, 0) - 1); 
    }

    public int pathSum(TreeNode root, int targetSum) {
        hash.put(0, 1);
        dfs(root, targetSum, 0);
        return ans;
    }
}

（哈希表+前缀和+递归）

class Solution {
    Map<Integer, Integer> map = new HashMap<>();
    int ans = 0;

    void dfs(TreeNode root, int targetSum, int sum) {
        if (map.containsKey(sum - targetSum))
            ans += map.get(sum - targetSum);
        map.put(sum, map.getOrDefault(sum, 0) + 1);
        if (root.left != null) dfs(root.left, targetSum, sum + root.left.val);
        if (root.right != null) dfs(root.right, targetSum, sum + root.right.val);
        map.put(sum, map.getOrDefault(sum, 0) - 1);
    }

    public int pathSum(TreeNode root, int targetSum) {
        if (root == null) return ans;
        map.put(0, 1);
        dfs(root, targetSum, root.val);
        return ans;
    }
}

475. 供暖器

（二分+排序+双指针）

本题的要求就是要我们求出供暖期的加热半径。

我们可以发现加热半径只会越来越大，不会减小。因为如果r=10可以覆盖所有的家庭那么r=20也一定可以覆盖所有的家庭。所以这个加热的半径是单调的。因此我们就可以使用二分找出加热的半径的长度。

当我们枚举半径的同时我们需要检查这个半径是否可以覆盖所有的家庭。我们可以把供暖期的加热半径看做一段区间。而我们需要做的是判断房子是否都在这些区间中。而因为供暖器的加热范围也是单调的，即如果从前往后的家庭不能受到一个供暖器的加热范围，那么一定那么这个供暖器前面一个供暖器也一定不能加热到这个房子。

因此房子和供暖器的位置是单调的，所以我们就可以使用双指针算法来判断是否加热器可以覆盖所有的房子。

class Solution {
    public int findRadius(int[] houses, int[] heaters) {
        Arrays.sort(houses);
        Arrays.sort(heaters);
        int l = 0, r = Integer.MAX_VALUE;
        while (l < r) {
            int mid = l + (r - l) / 2;
            if (check(mid, houses, heaters)) r = mid;
            else l = mid + 1;
        }
        return r;
    }
    public boolean check(int mid, int[] houses, int[] heaters) {
        for (int i = 0, j = 0; i < houses.length; i ++) {
            while (j < heaters.length && Math.abs(heaters[j] - houses[i]) > mid)
                j ++;
            if (j >= heaters.length) return false;
        }
        return true;
    }
}

（TreeSet）

还有一种方法是我们可以将供暖器放入TreeSet中，这样我们就可以找到一个房子左右两边的供暖器的位置。然后判断出两个位置的距离差的最小值就是我们需要的最小加热半径。将所有的这些最小加热半径去一个最大值就是全局的最小加热半径。

class Solution {
    public int findRadius(int[] houses, int[] heaters) {
        TreeSet<Integer> set = new TreeSet<>();
        for (int heater : heaters) {
            set.add(heater);
        }
        set.add(Integer.MIN_VALUE);
        set.add(Integer.MAX_VALUE);
        int ans = 0;
        for (int i = 0; i < houses.length; i ++) {
            int l = set.floor(houses[i]);
            int r = set.ceiling(houses[i]);
            ans = Math.max(ans, Math.min(Math.abs(l - houses[i]), Math.abs(r - houses[i])));
        }
        return ans;
    }
}

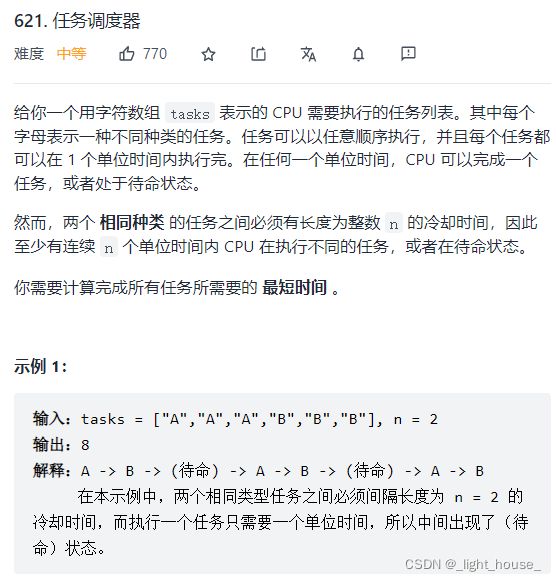
621. 任务调度器

（哈希表+贪心）

我们可以考虑最坏的情况。我们先挑出出现次数最多的字母，如果次数最多的字母都满足条件的话，那么其他的字母也一定可以满足。

假设出现次数最多的字母出现了maxCnt次，而每两个相同字母之间需要n个字母。所以为了使得该字母满足条件的话，需要(maxCnt - 1) * (n + 1) + 1次。如果出现maxCnt次的字母有k个的话，那么就需要(maxCnt - 1) * (n + 1) + k个字母。其余的字母就都可以放在出现最多的字母中间的空格即可。如果中间空格不够放，那么就可以在这些字母的后面添加列来摆放（如果不够放，说明其中有很多的字母都是不同的）。

class Solution {
    public int leastInterval(char[] tasks, int n) {
        HashMap<Character, Integer> hash = new HashMap<>();
        for (char ch : tasks) {
            hash.put(ch, hash.getOrDefault(ch, 0) + 1);
        }
        int maxCnt = 0, cnt = 0;
        for (Character c : hash.keySet()) {
            maxCnt = Math.max(maxCnt, hash.get(c));
        }
        for (Character c : hash.keySet()) {
            if (hash.get(c) == maxCnt) cnt ++;
        }
        return Math.max(tasks.length, (maxCnt - 1) * (n + 1) + cnt);
    }
}

（数组模拟哈希表+排序）

class Solution {
    public int leastInterval(char[] tasks, int n) {
        int[] cnt = new int[26];
        for (int i = 0; i < tasks.length; i ++) {
            cnt[tasks[i] - 'A'] ++;
        }
        Arrays.sort(cnt);
        int i = 25;
        int maxCnt = cnt[25];
        while (i >= 0 && maxCnt == cnt[i]) i --;
        return Math.max(tasks.length, (n + 1) * (maxCnt - 1) + 25 - i);
    }
}

​

129. 求根节点到叶节点数字之和

（递归）

本题就是一个很常规的遍历树的题目。

我们只需要在遍历一个树的时候，将每一条分支上的所有节点组成的字符串转化成一个整数即可。如果想要将要简单一点的话，可以直接通过num = num * 10 + root->val秦九韶方法直接算出结果即可。

注意细节：

1.我们只需要找到叶子节点即可，不要遍历到空，因为遍历到空的话，会因为有两个null节点而导致将最后一个节点计算了两次。

2.如果dfs(root->val)直接将root->val传过去的话，那么在进入每一层的时候，就会直接计算下一层的计算过了。如果dfs(0)的话，那么就是在当前层计算当前层上的节点，那么就需要在在判断是否为叶子节点之前就计算num = num * 1- + root->val。

class Solution {
public:
    int ans = 0;
    void dfs(TreeNode* root, int num) {
        if (!root->left && !root->right) {
            ans += num;
            return ;
        }
        if (root->left) dfs(root->left, num * 10 + root->left->val);
        if (root->right) dfs(root->right, num * 10 + root->right->val);
    }

    int sumNumbers(TreeNode* root) {
        dfs(root, root->val);
        return ans;
    }
};

（递归）

class Solution {
    int ans = 0;
    public void dfs(TreeNode root, int num) {
        num = num * 10 + root.val;
        if (root.left == null && root.right == null) {
            ans += num;
            return ;
        }
        if (root.left != null) dfs(root.left, num);
        if (root.right != null) dfs(root.right, num);
    }

    public int sumNumbers(TreeNode root) {
        dfs(root, 0);
        return ans;
    }
}

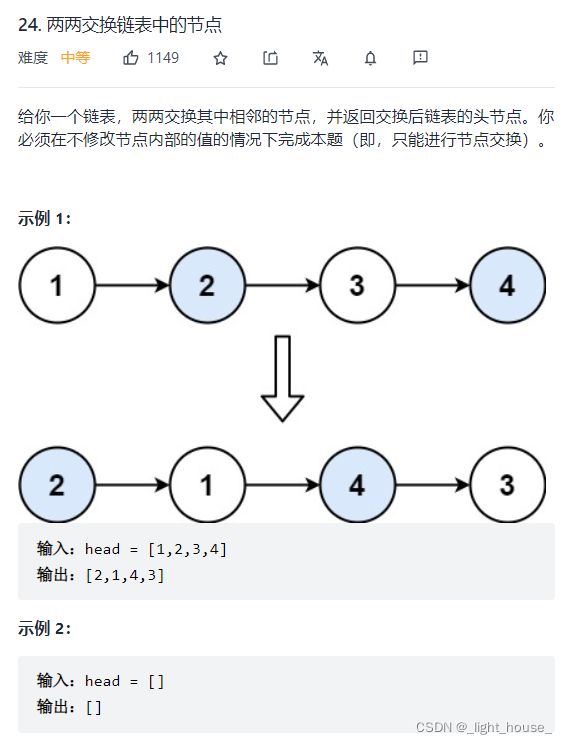
24. 两两交换链表中的节点

（局部反转链表）

因为每一次反转链表都需要和前面的节点有关联，而前两个节点没有前面的节点，所以我们可以创建一个虚拟的头结点，这样所以的节点都可以使用相同的操作了。

而反转两个节点只需要两个指针即可。然后每一次都只要将prev指针指向需要反转的两个节点的前面的节点即可（为了使得两个反转的节点和前面的链表的部分关联起来）。

class Solution {
    public ListNode swapPairs(ListNode head) {
        if (head == null || head.next == null) return head;
        ListNode dummy = new ListNode(-1);
        dummy.next = head;
        ListNode prev = dummy, cur = head;
        while (cur != null && cur.next != null) {
            ListNode next = cur.next;
            prev.next = next;
            cur.next = next.next;
            next.next = cur;
            prev = cur;
            cur = cur.next;
        }
        return dummy.next;
    }
}

1314. 矩阵区域和

（二维前缀和）

如果想要快速地求出一个矩阵中的和。也就是二维空间中的和，那么就可以使用二维前缀和。

二维前缀和数组需要通过pf[i][j] = pf[i - 1][j] + pf[i][j - 1] - pf[i - 1][j - 1] + mat[i - 1][j - 1];将(i, j)到(0,0)矩阵中的和浓缩成pf[i][j]。

回到题目中，我们需要求出以(i, j)为中心的，半径为1的矩阵的和。那么就是要求出ans[i - 1][j - 1] = get(pf, i - k - 1, j - k - 1) + get(pf, i + k, j + k) - get(pf, i - k - 1, j + k) - get(pf, i + k, j - k - 1);。

注意：很有可能以(i,j)为中心，半径为k的矩阵会越界，所以我们需要对坐标进行处理，使得pf[x][y]一定可以在矩阵中。

class Solution {
public:
    int get(vector<vector<int>>& pf, int x, int y) {
        int m = pf.size(), n = pf[0].size();
        x = min(m - 1, max(x, 0));
        y = min(n - 1, max(y, 0));
        return pf[x][y];        
    }

    vector<vector<int>> matrixBlockSum(vector<vector<int>>& mat, int k) {
        int m = mat.size(), n = mat[0].size();
        vector<vector<int>> pf(m + 1, vector<int>(n + 1));
        for (int i = 1; i <= m; i ++)
            for (int j = 1; j <= n; j ++)
                pf[i][j] = pf[i - 1][j] + pf[i][j - 1] - pf[i - 1][j - 1] + mat[i - 1][j - 1];
        
        vector<vector<int>> ans(m, vector<int>(n));
        for (int i = 1; i <= m; i ++) {
            for (int j = 1; j <= n; j ++) {
                int x1 = i - k - 1, y1 = j - k - 1;
                int x2 = i + k, y2 = j + k;
                int x3 = i + k, y3 = j - k - 1;
                int x4 = i - k - 1, y4 = j + k;
                ans[i - 1][j - 1] = get(pf, x2, y2) + get(pf, x1, y1) - get(pf, x3, y3) -
                get(pf, x4, y4);
            }
        }
        return ans;
    }
};

1239. 串联字符串的最大长度

（回溯）

我们只需要将所有的组合全部枚举一遍，然后检查每一种组合中是否存在重复元素即可。

class Solution {
public:
    int ans = 0;

    void dfs(vector<string>& arr, vector<bool>& vis, int start, int cnt) {
        int n = arr.size();
        ans = max(ans, cnt);
        for (int i = start; i < n; i ++) {
            bool flag = false;
            for (int j = 0; j < arr[i].size(); j ++) {
                if (vis[arr[i][j] - 'a']) {
                    flag = true;
                    for (int k = 0; k < j; k ++) vis[arr[i][k] - 'a'] = false;
                    break;
                } else {
                    vis[arr[i][j] - 'a'] = true;
                }
            }
            if (flag) continue;
            dfs(arr, vis, i + 1, cnt + arr[i].size());
            for (int j = 0; j < arr[i].size(); j ++)
                vis[arr[i][j] - 'a'] = false;
        }
    }
    
    int maxLength(vector<string>& arr) {
        vector<bool> vis(26);
        dfs(arr, vis, 0, 0);
        return ans;
    }
};

（位运算+递归回溯）

我们在回溯的过程中可以有两个优化：

1.我们可以首先预处理一下本身就有重复元素的字符串，并去重。

2.因为我们不关心字符串中的字符的位置，而只关心是否存在重复字符。所以我们可以使用一个int类型的整型判代替bool数组判空。

class Solution {
    int ans = 0;
    public int maxLength(List<String> arr) {
        List<Integer> masks = new ArrayList<>();
        // 将字符串中有重复字符的字符串去除掉
        for (String s : arr) {
            int mask = 0;
            for (int i = 0; i < s.length(); i ++) {
                int pos = s.charAt(i) - 'a';
                if ((mask & (1 << pos)) != 0) {
                    mask = 0;
                    break;
                }
                mask |= (1 << pos);
            }
            if (mask != 0)
                masks.add(mask);
        }
        dfs(masks, 0, 0);
        return ans;
    }
    public void dfs(List<Integer> masks, int mask, int index) {
        if (index == masks.size()) {
            ans = Math.max(ans, Integer.bitCount(mask));
            return ;
        }
        dfs(masks, mask, index + 1);
        if ((mask & masks.get(index)) == 0) {
            dfs(masks, mask | masks.get(index), index + 1);
        }
    }
}

740. 删除并获得点数

（哈希表+动规）

如果删除了nums[i]的话，那么nums[i] + 1和nums[i] - 1就会被跳过。这个就很像在打家劫舍中，小偷不可以偷两个相邻的房子是同样的道理。

因为删除一个数字一定是将所有相同的数字都删除掉，所以可以使用哈希表保存下来。而因此不能删除相邻的数字，所以我们使用动态规划将max(nums)中的所有的数字的取舍计算出来。

class Solution {
public:
    int deleteAndEarn(vector<int>& nums) {
        unordered_map<int, int> hash;
        int n = 0;
        for (int num : nums) {
            if (num > n) n = num;
            hash[num] ++;
        }
        vector<vector<int>> f(n + 1, vector<int>(2));
        for (int i = 1; i <= n; i ++) {
            if (hash.count(i)){
                f[i][1] = f[i - 1][0] + hash[i] * i;
            }
            f[i][0] = max(f[i - 1][1], f[i - 1][0]);
        }
        return max(f[n][0], f[n][1]);
    }
};

526. 优美的排列

（递归回溯）

class Solution {
    int ans = 0;
    public int countArrangement(int n) {
        boolean[] vis = new boolean[n];
        int[] nums = new int[n];
        for (int i = 0; i < n; i ++) nums[i] = i + 1;
        dfs(0, vis, nums, new ArrayList<Integer>());
        return ans;
    }

    public void dfs(int index, boolean[] vis, int[] nums, List<Integer> tmp) {
        int n = nums.length;
        if (index == n) {
            ans ++;
            return ;
        }
        for (int i = 0; i < n; i ++) {
            if (vis[i]) continue;
            if (!(nums[i] % (index + 1) == 0 || (index + 1) % nums[i] == 0)) continue;
            vis[i] = true;
            tmp.add(i);
            dfs(index + 1, vis, nums, tmp);
            tmp.remove(tmp.size() - 1);
            vis[i] = false;
        }
    }
}

（递归回溯）

class Solution {
    int ans = 0;
    public int countArrangement(int n) {
        boolean[] vis = new boolean[n + 1];
        dfs(n, 1, vis);
        return ans;
    }

    public void dfs(int n, int index, boolean[] vis) {
        if (index > n) {
            ans ++;
            return ;
        }
        for (int num = 1; num <= n; num ++) {
            if (vis[num]) continue;
            if (!(num % index == 0 || index % num == 0)) continue;
            vis[num] = true;
            dfs(n, index + 1, vis);
            vis[num] = false;
        }
    }
}

（递归回溯+位运算状态压缩）

class Solution {
    int ans = 0;
    public int countArrangement(int n) {
        dfs(n, 1, 0);
        return ans;
    }

    public void dfs(int n, int index, int mask) {
        if (index > n) {
            ans ++;
            return ;
        }
        for (int num = 1; num <= n; num ++) {
            if ((mask & (1 << num)) != 0) continue;
            if (!(num % index == 0 || index % num == 0)) continue;
            mask |= (1 << num);
            dfs(n, index + 1, mask);
            mask &= ~(1 << num);
        }
    }
}

（状态压缩+DP优化）

class Solution {
    public int countArrangement(int n) {
        int mask = 1 << n;
        int[] f = new int[mask];
        f[0] = 1;
        for (int i = 0; i < mask; i ++) {
            int t = Integer.bitCount(i);
            for (int k = 1; k <= n; k ++) {
                if (((1 << (k - 1)) & i) != 0) {
                    if (t % k == 0 || k % t == 0) {
                        f[i] += f[i & ~(1 << (k - 1))];
                    }
                }
            }
        }
        return f[mask - 1];
    }
}

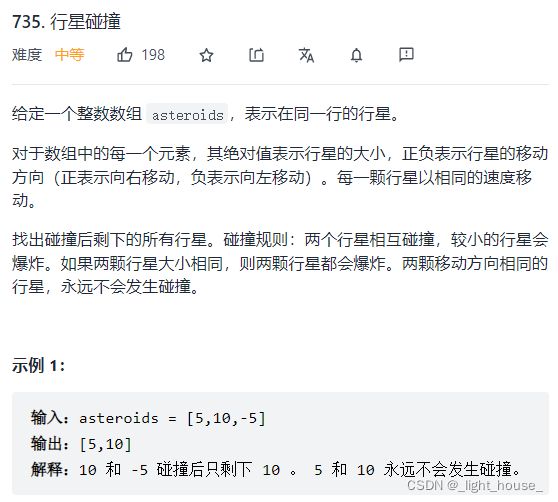
735. 行星碰撞

（栈）

本题是一个模拟题，也可以是一个使用栈的题目。我们只需要判断下一个行星的方向的质量即可。1.我们将向右的行星直接放入栈中。2.1.如果是向左的行星的话，就需要处理宇向右移动行星的相撞的问题。即当nums[i] < 0的时候，if(!sk.empty() && sk.top() > 0 && sk.top() < -nums[i])的时候，需要将nums[i]弹出。2.2.如果sk.top() == -nums[i]的话，就将两个行星都销毁。2.3.如果sk.empty() || sk.top() < 0即如果栈中已经空了或者栈中的行星都是向左的，那么就直接将行星插入到栈中，2.4.否则的话说明栈中的行星要比当前的行星的质量要大，那么就销毁当前的行星也就是不将这个行星插入到栈中。

class Solution {
    public int[] asteroidCollision(int[] nums) {
        Stack<Integer> stack = new Stack<>();
        int n = nums.length;
        for (int i = 0; i < n; i ++) {
            if (nums[i] > 0 || stack.isEmpty() || stack.peek() < 0) {
                stack.add(nums[i]);
            } else {
                // 处理行星相撞的部分
                if (-nums[i] >= stack.peek()) {
                    while (!stack.isEmpty() && stack.peek() > 0 && -nums[i] > stack.peek()) {
                        stack.pop();
                    }
                    if (stack.isEmpty() || stack.peek() < 0) {
                        stack.add(nums[i]);
                    } else if (-nums[i] == stack.peek()) {
                        stack.pop();
                    }
                }
                // 如果-nums[i] < 栈顶的话直接不用添加
            }
        }
        int[] ans = new int[stack.size()];
        for (int i = ans.length - 1; i >= 0; i --) {
            ans[i] = stack.pop();
        }
        return ans;
    }
}

95. 不同的二叉搜索树 II

（递归）

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<TreeNode*> generateTrees(int n) {
        if (!n) return {};
        return dfs(1, n);
    }
    vector<TreeNode*> dfs(int start, int end) {
        if (start > end) {
            return {nullptr};
        }
        vector<TreeNode*> ans;
        for (int i = start; i <= end; i ++) {
            auto lefts = dfs(start, i - 1);
            auto rights = dfs(i + 1, end);
            for (auto l : lefts) {
                for (auto& r : rights) {
                    TreeNode* node = new TreeNode(i);
                    node->left = l;
                    node->right = r;
                    ans.push_back(node);
                }
            }
        }
        return ans;
    }
};

1877. 数组中最大数对和的最小值

（排序+贪心）

class Solution {
public:
    int minPairSum(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int l = 0, r = nums.size() - 1;
        int ans = 0;
        for (int l = 0, r = nums.size() - 1; l < r; l ++, r --) {
            ans = max(ans, nums[l] + nums[r]);
        }
        return ans;
    }
};

208. 实现 Trie (前缀树)

（字典树）

trie树就是一个树枝上都是字母构成的一棵树。通过trie存储单词的话可以是的多个单词使用同一个字母表。这样就可以大大地提高查找效率。并且找到一个单词的前缀。存储思路：使用一个结构体，其中可以存放一个存放trie的数组tree，这样就可以通过node->tree[index]找到下一个树枝上的节点。并且结构体中包含一个标志位isEnd表示这个节点是否为单词的最后一个节点，这样就可以判断单词是否存在于这棵树中。

class Trie {
    class Node {
        Node[] tree;
        boolean isEnd;
        Node() {
            tree = new Node[26];
            isEnd = false;
        }
    }
    public Node root;
    
    public Trie() {
        root = new Node();
    }
    
    public void insert(String word) {
        Node cur = root;
        for (int i = 0; i < word.length(); i ++) {
            int u = word.charAt(i) - 'a';
            if (cur.tree[u] == null) 
            				cur.tree[u] = new Node();
            cur = cur.tree[u];
        }
        cur.isEnd = true;
    }
    
    private Node helper(String str) {
        Node cur = root;
        for (int i = 0; i < str.length(); i ++) {
            int u = str.charAt(i) - 'a';
            if (cur.tree[u] == null) return null;
            cur = cur.tree[u];
        }
        return cur;
    }
    
    public boolean search(String word) {
        Node node = helper(word);
        return node != null && node.isEnd == true;
    }
    
    public boolean startsWith(String prefix) {
        Node node = helper(prefix);
        return node != null;
    }
}

/**
 * Your Trie object will be instantiated and called as such:
 * Trie obj = new Trie();
 * obj.insert(word);
 * boolean param_2 = obj.search(word);
 * boolean param_3 = obj.startsWith(prefix);
 */

1218. 最长定差子序列

（哈希表+动态规划）

本题是一个简单的动态规划的题目，有一点像求最长上升子序列的长度。但是如果想要快速的在前i个数字中找到nums[i] - difference对应的次数的话，就需要使用哈希表记录下nums[i]对应的等差子序列的最长长度。这样在计算以nums[i]结尾的最长等差子序列的长度的时候，就可以使用hash[nums[i] - difference]计算了。

class Solution {
public:
    int longestSubsequence(vector<int>& arr, int difference) {
        int n = arr.size();
        vector<int> f(n, 1);
        unordered_map<int, int> hash;
        int ans = 0;
        for (int i = 0; i < n; i ++) {
            int tmp = arr[i] - difference;
            if (hash.count(tmp)) {
                f[i] += hash[tmp];
            }
            hash[arr[i]] = f[i];
            ans = max(ans, f[i]);
        }
        return ans;
    }
};

（哈希表+动规）

class Solution {
public:
    int longestSubsequence(vector<int>& arr, int difference) {
        int n = arr.size();
        unordered_map<int, int> hash;
        int ans = 0;
        for (int i = 0; i < n; i ++) {
            int tmp = arr[i] - difference;
            hash[arr[i]] = hash[tmp] + 1;
            ans = max(ans, hash[arr[i]]);
        }
        return ans;
    }
};

443. 压缩字符串

（双指针）

本题就是一个典型的双指针问题。我们只需要将连续的字符的个数通过双指针的方式统计出来。然后再覆盖式地填写在原字符数组中即可。

class Solution {
    public int compress(char[] chars) {
        int n = chars.length;
        int index = 0;
        for (int i = 0; i < n; i ++) {
            int j = i;
            while (j < n && chars[j] == chars[i]) j ++;
            chars[index ++] = chars[i];
            if (j != i + 1) {
                String str = String.valueOf(j - i);
                for (int k = 0; k < str.length(); k ++) {
                    chars[index ++] = str.charAt(k);
                }
            }
            i = j - 1;
        }
        return index;
    }
}

（双指针）

class Solution {
    public int compress(char[] chars) {
        int n = chars.length;
        int index = 0;
        for (int i = 0; i < n; i ++) {
            int j = i;
            while (j < n && chars[j] == chars[i]) j ++;
            chars[index ++] = chars[i];
            if (j > i + 1) {
                int num = j - i;
                int k = index;
                while (num != 0) {
                    chars[index ++] = (char)(num % 10 + '0');
                    num /= 10;
                }
                reverse(chars, k, index - 1);
            }
            i = j - 1;
        }
        return index;
    }
    public void reverse(char[] chars, int l, int r) {
        while (l < r) {
            char tmp = chars[l];
            chars[l] = chars[r];
            chars[r] = tmp;
            l ++;
            r --;
        }
    }
}

581. 最短无序连续子数组

（双指针+贪心）

我们需要找出中间一段需要排序的序列的话，首先需要观察这段无序的序列的性质。可以发现这个序列的最小值要比前面一段有序序列的最后一个数字要大，这段无序序列的最大值要比后面一段有序序列的第一个数字要小。

因此我们可以首先找到转折之后的最大值和最小值，然后将前后序列中有序的部分跳过。

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int max = Integer.MIN_VALUE, min = Integer.MAX_VALUE;
        int n = nums.length;
        for (int i = 1; i < n; i ++) {
            if (nums[i] < nums[i - 1]) {
                max = Math.max(max, nums[i - 1]);
                min = Math.min(min, nums[i]);
            }
        } 
        int i = 0;
        while (i < n && nums[i] <= min) i ++;
        int j = n - 1;
        while (j >= 0 && nums[j] >= max) j --;
        return j - i + 1 <= 0 ? 0 : j - i + 1;
    }
}

（双指针+贪心）

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int n = nums.length;
        int l = 0;
        // 找前面一个序列中的最大值
        while (l + 1 < n && nums[l + 1] >= nums[l]) l ++;
        if (l == n - 1) return 0;
        int r = n - 1;
        // 找后面一个序列中的最小值
        while (r - 1 >= 0 && nums[r - 1] <= nums[r]) r --;
        // 根据后面的数字，将前面有序序列的区间缩小
        for (int i = l + 1; i < n; i ++)
            while (l >= 0 && nums[i] < nums[l]) 
                l --;
		// 根据前面的数组，将后面有序序列的区间缩小
        for (int i = r - 1; i >= 0; i --)
            while (r < n && nums[i] > nums[r])
                r ++;
        return r - l - 1;
    }
}

（排序 + 双指针）

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int[] tmp = nums.clone();
        Arrays.sort(tmp);
        int i = 0;
        while (i < nums.length && tmp[i] == nums[i]) i ++;
        int j = nums.length - 1;
        while (j >= 0 && tmp[j] == nums[j]) j --;
        return j - i + 1 < 0 ? 0 : j - i + 1;
    }
}

229. 求众数 II

（摩尔投票法）

摩尔投票法是一个解决求出众数的方法。

本题是「多数元素」的进阶版题目，本题要求求出出现次数超过n/3次的元素。首先我们要明确一个数组中如果存在超过n/3次的元素，那么这个元素的个数一定不超过两个。因为如果有3个即以上的元素出现次数都超过了n/3，那么数字的个数就超过n了。

所以可以使用num1和num2表示数组中的众数，并且使用cnt1和cnt2记录num1和num2出现的次数。如果在遍历数组的过程中发现cnt1或则cnt2为0了，那么就用nums[i]替代num1或者num2。如果发现nums[i]等于num1或者num2的话，就将对应数字的次数+1。如果不相等就将数字对应的次数-1。

这就相当于不同的数字之间相互抵消，相同的数字之间可以增加出现的次数。最后剩下来的就是在数组中出现次数超过n/3的数字。

注意：一定需要先判断if (cnt != 0 && num1 == nums[i])和if (cnt2 != 0 && num2 == nums[i])，而不能先判断if (cnt1 == 0)和if (cnt2 == 0)。这是因为如果nums[i] == num2但是先判断了cnt1 == 0的话，那么此时num1 = num2 = nums[i]。这就出错了。所以我们需要先判断nums[i]是否和num1或者num2其中的一个相等。如果相等的话，那么就直接将对应数字的次数+1即可。

class Solution {
    public List<Integer> majorityElement(int[] nums) {
        int num1 = 0, num2 = 0, cnt1 = 0, cnt2 = 0;
        for (int i = 0; i < nums.length; i ++) {
            // 如果num1 == nums[i]并且cnt1不等于0
            if (cnt1 != 0 && num1 == nums[i]) cnt1 ++;
            // 如果num2 == nums[i]并且cnt2不等于0
            else if (cnt2 != 0 && num2 == nums[i]) cnt2 ++;
            // 如果cnt1 == 0
            else if (cnt1 == 0) {
                num1 = nums[i];
                cnt1 = 1;
            } else if (cnt2 == 0) { // 如果cnt2 == 0
                num2 = nums[i];
                cnt2 = 1;
            } else { // 如果cnt1!=0&&cnt2!=0&&nums[i]!=num1&&nums[i]!=num2
                cnt1 --;
                cnt2 --;
            }
        }
        // 判断数字重复的次数是否大于n/3
        List<Integer> ans = new ArrayList<>();
        cnt1 = 0; cnt2 = 0;
        for (int num : nums) {
            if (num == num1) cnt1 ++;
            else if (num == num2) cnt2 ++;
        }
        if (cnt1 > nums.length / 3) ans.add(num1);
        if (cnt2 > nums.length / 3) ans.add(num2);
        return ans;
    }
}

274. H 指数

（二分+排序）

class Solution {
public:
    int hIndex(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        int r = nums.back();
        int ans = 0;
        while (r >= 0) {
            auto it = lower_bound(nums.begin(), nums.end(), r);       
            int cnt = nums.end() - it;
            ans = max(ans, min(cnt, r));
            r --;
        }
        return ans;
    }
};

（排序+二分）

我们要找到最大的h，使得h篇论文至少被引用了h次。

所以我们只需要将数组排序。二分的搜索h即可。即mid右边的数字引用的次数应该< mid，而mid左边的数字引用的次数应该>= mid。这样就可以找到最大的h，使得h篇论文至少被引用了h次。

class Solution {
    public int hIndex(int[] nums) {
        Arrays.sort(nums);
        int l = 0, r = nums.length;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (check(nums, mid)) l = mid;
            else r = mid - 1;
        }
        return l;
    }
    public boolean check(int[] nums, int mid) {
        int cnt = 0; // 第mid篇论文被引用的次数
        for (int num : nums)
            if (num >= mid) 
                cnt ++;
        return cnt >= mid; 
    }
}

930. 和相同的二元子数组

（哈希表+前缀和）

如果我们想要快速地判断是否一个数组中存在一段区间的和为target的话，就可以使用前缀和+哈希表。

使用普通的前缀和可以通过两层循环枚举区间的左右端点，从而判断是否存在是否存在一段和为target的区间。

但是如果使用前缀和+哈希表就可以在O(N)的时间内判断是否存在一段区间的和为target。因为sum[r] - sum[l] = target，所以sum[l] = sum[r] - target。如果我们将前面的s[l]都保存在哈希表中，那么我们在枚举r的时候，就可以通过判断s[r] - target是否在哈希表中判断是否存在区间和target，因为s[r] - target = sum[l]。

注意：要记得将0插入到哈希表中，因为如果当sum[i] == goal的时候，0应该是在哈希表中的。

class Solution {
    public int numSubarraysWithSum(int[] nums, int goal) {
        int n = nums.length;
        int[] sum = new int[n + 1];
        for (int i = 1; i <= n; i ++) {
            sum[i] = sum[i - 1] + nums[i - 1];
        }
        Map<Integer, Integer> hash = new HashMap<>();
        int ans = 0;
        hash.put(0, 1);
        for (int i = 1; i <= n; i ++) {
            if (hash.containsKey(sum[i] - goal)) {
                ans += hash.get(sum[i] - goal);
            }
            hash.put(sum[i], hash.getOrDefault(sum[i], 0) + 1);
        }
        return ans;
    }
}

class Solution {
    public int numSubarraysWithSum(int[] nums, int goal) {
        int n = nums.length;
        Map<Integer, Integer> hash = new HashMap<>();
        int ans = 0;
        hash.put(0, 1);
        for (int i = 1, sum = 0; i <= n; i ++) {
            sum += nums[i - 1];
            if (hash.containsKey(sum - goal)) {
                ans += hash.get(sum - goal);
            }
            hash.put(sum, hash.getOrDefault(sum, 0) + 1);
        }
        return ans;
    }
}

856. 括号的分数

（栈）

使用栈可以用来匹配两个平衡的括号。当时这里我们可以在栈中存放0，表示括号中的分值。

如果ch == ‘(’，则说明新增加一个括号，即sk.add(0)。

如果ch == ')'，则我们需要对括号中的数字进行处理。

​ 如果sk.pop() == 0，说明当前的括号是()，则括号中的值+1即可。

​ 如果sk.pop() != 0，说明当前括号中的是(A)，则需要对括号中的值需要*2。

​ 并且我们需要将top + sk.pop()放入栈中，因为sk.peek()也是括号中的值，所以我们需要将所有括号中的是都放在一起。

class Solution {
    public int scoreOfParentheses(String s) {
        Stack<Integer> sk = new Stack<>();
        sk.add(0);
        for (int i = 0; i < s.length(); i ++) {
            char ch = s.charAt(i);
            if (ch == '(') {
                sk.add(0);
            } else {
                int top = sk.pop();
                if (top == 0) top += 1;
                else top *= 2;
                // 将当前的值加到当前数字所在的括号中
                sk.add(sk.pop() + top);
            }
        }
        return sk.peek();
    }
}

166. 分数到小数

（数学 + 哈希表）

本题其实就是需要我们求出两个数字需要相除的小数部分的数字。

1.我们要知道两个数字相除的话可能会超出int的范围，所以我们需要使用long来存储。

2.因为我们只计算两个正数的除法，所以需要先特判两个数字的正负号。

3.首先我们可以先将两个数子可以直接相除的部分转换成数字的整数部分。然后就是保留x的余数的部分（假设是x/y）一直和y相除，直到x等于0为止或者出现了重复的数字（出现了循环小数）。

class Solution {
    public String fractionToDecimal(int numerator, int denominator) {
        long x = numerator, y = denominator;
        if (x % y == 0) {
            return String.valueOf(x / y);
        }
        StringBuffer ans = new StringBuffer();
        if ((x > 0) ^ (y > 0)) ans.append('-');
        x = Math.abs(x);
        y = Math.abs(y);        
        ans.append(String.valueOf(x / y));
        x %= y;
        ans.append('.');
        Map<Long, Integer> hash = new HashMap<>();
        while (x != 0) {
            hash.put(x, ans.length());
            x *= 10;
            ans.append(String.valueOf(x / y));
            x %= y;
            if (hash.containsKey(x)) {
                int index = hash.get(x);
                return (ans.substring(0, index) + "(" + ans.substring(index) + ")");
                //return String.format("%s(%s)", ans.substring(0, hash.get(x)),ans.substring(hash.get(x)));
            }
        }
        return ans.toString();
    }
}

767. 重构字符串

（贪心+哈希表）

我们要知道如果一个字符ch出现的次数大于(s.length() + 1) / 2的话，那么一定不可能重构字符串。否则就可以重构字符串。

而且因为可能字符串的长度为奇数，所以出现次数最多的字符就需要放在偶数位上，这样才可以使得所有的字符都不相邻。至于其他的字符就可以从奇数位开始放，如果奇数位置上都放满的话，也可以放在偶数位置的空余位置上。

class Solution {
    public String reorganizeString(String s) {
        int t = (s.length() + 1) / 2;
        Map<Character, Integer> hash = new HashMap<>();
        for (int i = 0; i < s.length(); i ++) {
            char ch = s.charAt(i);
            hash.put(ch, hash.getOrDefault(ch, 0) + 1);
            if (hash.get(ch) > t) return "";
        }
        char[] str = new char[s.length()];
        int even = 0, odd = 1;
        int n = s.length();
        for (char ch = 'a'; ch <= 'z'; ch ++) {
            if (hash.containsKey(ch) && hash.get(ch) <= n / 2) {
                while (hash.containsKey(ch) && hash.get(ch) != 0 && odd < n) {
                    str[odd] = ch;
                    hash.put(ch, hash.getOrDefault(ch, 0) - 1);
                    if (hash.get(ch) == 0) hash.remove(ch);
                    odd += 2;
                }
            } 
            while (hash.containsKey(ch) && hash.get(ch) != 0 && even < n) {
                str[even] = ch;
                hash.put(ch, hash.getOrDefault(ch, 0) - 1);
                if (hash.get(ch) == 0) hash.remove(ch);
                even += 2;
            }
        }
        return new String(str);
    }
}