AcWing 1275. 最大数—线段树单点修改

题目链接 AcWing 1275. 最大数

题目描述

分析
这道题是线段树的模板题，属于一眼ding真，鉴定为线段树的裸题，正好用来学习线段树。线段树、树状数组等数据结构题，难的地方是在如何分析出来要用哪个数据结构解决。
线段树要比树状数组要好理解一些，但是线段树的代码难写一些，且支持的操作多一些。线段树是以区间来考虑问题，保存的基本信息有区间的左边界、右边界、区间的属性(sum、min、max…)等等。

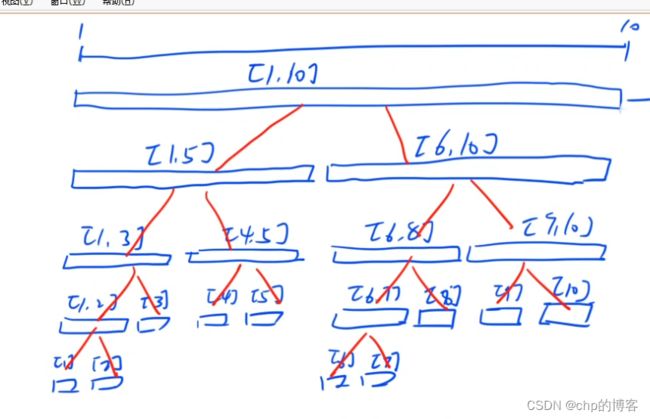
拿区间[1,10]举例，可分为如图所示的小区间，由于这里和堆很像，所以也是用数组来存所有的点，最多不超过4n个区间。能使用线段树的题有一些特点，就是大区间的属性能从小区间得到，比如求max，max([1,10])=max{max([1,5]),max(6,10)}，线段树一共有4个基本操作，分别是
build:建立线段树
pushup:由两个子区间更新父区间，例如max([1,10])=max{max([1,5]),max(6,10)}
query:查询某区间
modify:修改某个点(这里只考虑单点修改，不考虑区间修改需要的懒标记pushdown操作)

一般用结构体来保存信息,需要4n个点

struct E{
    int l,r,v;
}tr[N*4];

build操作就是建立线段树，代码如下，类似于建堆的过程

void build(int u,int l,int r){
    tr[u].l=l;//当前区间的左边界
    tr[u].r=r;//当前区间的右边界
    if(l==r) return;//当前节点为叶子节点，则返回
    int mid=l+r>>1;
    build(u<<1,l,mid);//建立左子边界
    build(u<<1|1,mid+1,r);//建立右子边界
}

pushup:由两个子区间更新父区间，代码如下

void pushup(int u){
    tr[u].v=max(tr[u<<1].v,tr[u<<1|1].v);//这里是求区间max
}

query:查询某区间，代码如下

int query(int u,int l,int r){
    if(l<=tr[u].l&&r>=tr[u].r) return tr[u].v;//如果查询的区间包含了线段树的区间，则返回该线段树区间的值
    int mid=tr[u].l+tr[u].r>>1;
    int v=0;
    if(l<=mid) v=query(u<<1,l,r);//这里是求区间max
    if(r>mid) v=max(v,query(u<<1|1,l,r));
    return v;
}

modify:修改某个点(这里只考虑单点修改，不考虑区间修改需要的懒标记pushdown操作)

void modify(int u,int x,int v){//修改和查询类似
    if(tr[u].l==x&&tr[u].r==x) tr[u].v=v;
    else{
        int mid=tr[u].l+tr[u].r>>1;
        if(x<=mid) modify(u<<1,x,v);
        else modify(u<<1|1,x,v);
        pushup(u);//这里修改了叶子节点之后要回溯更新一下父节点，否则父节点保存的信息还是之前的信息
    }
}

代码如下:

#include
#include
#include
#include
using namespace std;
typedef long long ll;
const int N=2e5+10;

struct E{
    int l,r,v;
}tr[N*4];
int m,p;

void build(int u,int l,int r){
    tr[u].l=l;
    tr[u].r=r;
    if(l==r) return;
    int mid=l+r>>1;
    build(u<<1,l,mid);
    build(u<<1|1,mid+1,r);
}
void pushup(int u){
    tr[u].v=max(tr[u<<1].v,tr[u<<1|1].v);
}
int query(int u,int l,int r){
    if(l<=tr[u].l&&r>=tr[u].r) return tr[u].v;
    int mid=tr[u].l+tr[u].r>>1;
    int v=0;
    if(l<=mid) v=query(u<<1,l,r);
    if(r>mid) v=max(v,query(u<<1|1,l,r));
    return v;
}
void modify(int u,int x,int v){
    if(tr[u].l==x&&tr[u].r==x) tr[u].v=v;
    else{
        int mid=tr[u].l+tr[u].r>>1;
        if(x<=mid) modify(u<<1,x,v);
        else modify(u<<1|1,x,v);
        pushup(u);
    }
}
int main(){
    int n=0,last=0;
    cin>>m>>p;
    build(1,1,m);
    while(m--){
        char op[2];
        int x;
        scanf("%s%d",op,&x);
        if(*op=='Q'){
            last=query(1,n-x+1,n);
            cout<<last<<endl;
        }
        else{
            modify(1,n+1,((ll)last+x)%p);
            n++;
        }
    }
    return 0;
}