全加器(多位)的实现
一,半加器
-
定义
半加器(Half Adder)是一种用于执行二进制数相加的简单逻辑电路。它可以将两个输入位的和(Sum)和进位(Carry)计算出来。
半加器有两个输入:A 和 B,分别代表要相加的两个二进制位。它的输出由两个部分组成:
1.和(Sum):表示 A + B 的个位数结果。
2.进位(Carry):表示 A + B 的十位数结果是否需要进位到下一位。 -
逻辑表达式
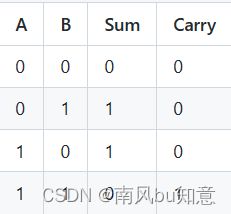
根据真值表可知,当 A 和 B 的输入都为 0 时,Sum 和 Carry 均为 0;当 A 和 B 的输入中有一个为 1 时,Sum 为 1,Carry 为 0;当 A 和 B 的输入都为 1 时,Sum 为 0,Carry 为 1。所以其逻辑表达式为:
Sum = A ^ B
Carry = A & B -
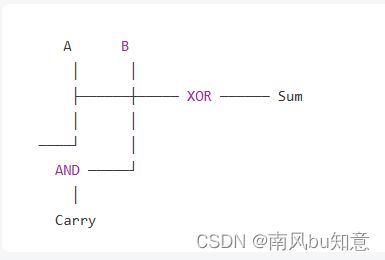
逻辑电路
- Verilog代码实现
module half_adder(
input wire a_in ,
input wire b_in ,
output wire count ,//进位
output wire sum //半加和数
);
assign count = a_in & b_in;
assign sum = a_in ^ b_in;
// assign = {count,sum} = a_in + b_in ;
endmodule
- tb文件
`timescale 1ns/1ns
module tb_half_adder();
reg in_a;
reg in_b;
wire count;
wire sum;
initial begin
in_a = 0;
in_b = 0;
#10;
repeat(100)begin
in_a =($random);
in_b =($random);
#10;
end
#10;
$stop;
end
half_adder u_half_adder(
.a_in (in_a),
.b_in (in_b),
.count (count),//进位
.sum (sum) //半加和数
);
endmodule
二,全加器
- 定义
全加器(Full Adder)是一种用于执行二进制数相加的数字逻辑电路。与半加器相比,全加器能够处理两个输入位之间的进位,从而实现多位二进制数的相加运算。
一个全加器有三个输入:A、B 和进位(Carry-In,通常用Cin表示),代表要相加的两个二进制位和上一位的进位。它的输出由两部分组成:
1.和(Sum):表示 A + B + Cin 的个位数结果。
2.进位(Carry-Out,通常用Cout表示):表示 A + B + Cin 的十位数结果是否需要进位到下一位。 - 真值表
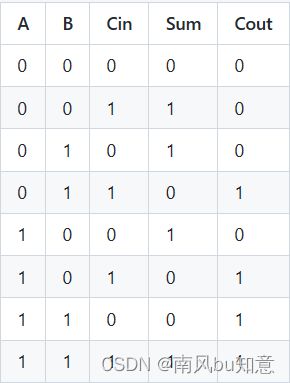
- 逻辑表达式
全加器的逻辑表达式可以通过使用逻辑门(AND、XOR)来表示。以下是全加器的逻辑表达式:
Sum = A ^ B ^ Cin
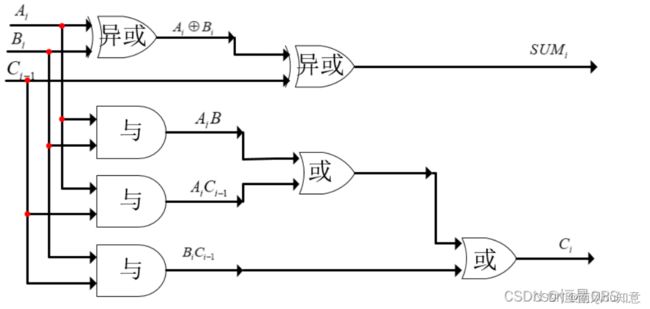
Cout = (A ^ B)&Cin + A&B - 逻辑电路(这里借用一下别人的图阿里嘎多)
- Verilog代码
module full_adder(
input wire a_in,
input wire b_in,
input wire c_in,
output wire count,
output wire sum
);
// reg count_r;
// reg sum_r;
assign sum = a_in ^ b_in ^ c_in;
assign count = (a_in ^ b_in)&c_in | a_in&b_in;
//{count , sum} = a_in + b_in + c_in
endmodule
- tb文件
module full_adder(
input wire a_in,
input wire b_in,
input wire c_in,
output wire count,
output wire sum
);
// reg count_r;
// reg sum_r;
assign sum = a_in ^ b_in ^ c_in;
assign count = (a_in ^ b_in)&c_in | a_in&b_in;
//{count , sum} = a_in + b_in + c_in
endmodule
三,多位全加器
- 个人理解
对于多位全加器我的理解是,相当于多位数的每一位都是一个全加器,所以对于多位全加器,就是相当于是多个全加器的连接。 - verilog代码实现(generate)
module N_adder #(parameter N = 2) (
input [N-1:0] a_in,
input [N-1:0] b_in,
input cin,
output [N-1:0] sum,
output count
);
wire [N:0] c;
genvar i;
generate
for (i = 0;i<N ; i=i+1)
begin : adder_full_n
full_adder full_adder_inst (
.a_in (a_in[i]),
.b_in (b_in[i]),
.c_in (c[i]),
.sum (sum[i]),
.count (c[i+1])
);
end
endgenerate
assign c[0] = cin;
assign count = c[N];
endmodule
- tb文件
`timescale 1ns/1ns
module N_adder_tb ();
parameter N = 5;
reg [N-1:0] a_in;
reg [N-1:0] b_in;
reg cin;
wire [N-1:0] sum;
wire count;
initial begin
cin = 1'b0;
#5;
repeat(20)begin
a_in =($random)%5;
b_in =($random)%5;
#(5);
end
#(10)
$stop;
end
N_adder #(.N(N)) N_adder_inst (
.a_in (a_in),
.b_in (b_in),
.cin (cin),
.sum (sum),
.count (count)
);
endmodule
四,总结
对于全加器,还是比较好理解的,主要是对组合逻辑的考察和理解,只要对组合逻辑有一定的理解我相信全加器还是比较好理解的。