c++ 医院设置

题目描述

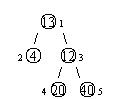
设有一棵二叉树，如图：

其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为 11。如上图中，若医院建在1 处，则距离和 =4+12+2\times20+2\times40=136=4+12+2×20+2×40=136；若医院建在 33 处，则距离和 =4\times2+13+20+40=81=4×2+13+20+40=81。

输入格式

第一行一个整数 nn，表示树的结点数。

接下来的 nn 行每行描述了一个结点的状况，包含三个整数 w, u, vw,u,v，其中 ww 为居民人口数，uu 为左链接（为 00 表示无链接），vv 为右链接（为 00 表示无链接）。

输出格式

一个整数，表示最小距离和。

输入输出样例

输入 #1复制

5						
13 2 3
4 0 0
12 4 5
20 0 0
40 0 0

输出 #1复制

81

说明/提示

数据规模与约定

对于 100\%100% 的数据，保证 1 \leq n \leq 1001≤n≤100，0 \leq u, v \leq n0≤u,v≤n，1 \leq w \leq 10^51≤w≤105。

1.

现有的题解基本是用Floyed或者其他稍优的算法跑的，其时间复杂度均在O(n^2)O(n2)以上。

那么问题来了，

你们经历过绝望吗

这题作为我们图论考试的一道题，n的范围直接到了10000，此时N^2的算法也无法AC。

有句写居里夫人的话：“别人摸瓜她寻藤，别人摘叶他问根”

我们也要做那个“她”， 不能只满足于通过此题，而且要了解本题的O(N)O(N)算法正解：带权树的重心。

树的重心的定义：

树若以某点为根，使得该树最大子树的结点数最小，那么这个点则为该树的重心，一棵树可能有多个重心。

树的重心的性质：

1、树上所有的点到树的重心的距离之和是最短的，如果有多个重心，那么总距离相等。

2、插入或删除一个点，树的重心的位置最多移动一个单位。

3、若添加一条边连接2棵树，那么新树的重心一定在原来两棵树的重心的路径上。

当然，这题我们只需要用到第一条性质。

怎么求树的重心：

定义几个数组：f[u]f[u]表示以u为根的总距离，size[u]size[u]表示以u为根的子树的大小（结点数，此题每个点要乘以权值，下文结点数均指此）。

显然，ans=min(f[i],1<=i<=n)ans=min(f[i],1<=i<=n)

首先我们任意以一个点为根dfs一遍，求出以该点为根的总距离。方便起见，我们就以1为根。

接下来就是转移，对于每个u能达到的点v，有：

f[v]=f[u]+size[1]-size[v]-size[v]f[v]=f[u]+size[1]−size[v]−size[v]

怎么来的呢？试想，当根从u变为v的时候，v的子树的所有节点原本的距离要到uu，现在只要到vv了，每个结点的距离都减少1，那么总距离就减少size[v]size[v]，同时，以v为根的子树以外的所有节点，原本只要到uu就行了，现在要到vv，每个节点的路程都增加了1，总路程就增加了size[1]-size[v]size[1]−size[v]，其中size[1]size[1]就是我们预处理出来的整棵树的大小，减去size[v]size[v]就是除以v为根的子树以外的结点数。

最后取最小值，得解。时间复杂度O(n)O(n)

附上代码：

#include 
#define rep(i, m, n) for(register int i = m; i <= n; ++i)
#define INF 2147483647
#define Open(s) freopen(s".in","r",stdin);freopen(s".out","w",stdout);
#define Close fclose(stdin);fclose(stdout);
using namespace std;
inline int read(){
	int s = 0, w = 1;
	char ch = getchar();
	while(ch < '0' || ch > '9') { if(ch == '-') w = -1; ch = getchar(); }
	while(ch >= '0' && ch <= '9') { s = s * 10 + ch - '0'; ch = getchar(); }
	return s * w;
}
const int MAXN = 10010;
struct Edge{
	int next, to;
}e[MAXN << 1];
int head[MAXN], num, w[MAXN], n, size[MAXN];
long long ans = INF, f[MAXN];
inline void Add(int from, int to){
	e[++num].to = to;
	e[num].next = head[from];
	head[from] = num;
}
void dfs(int u, int fa, int dep){ //预处理f[1]和size
    size[u] = w[u];
	for(int i = head[u]; i; i = e[i].next){
	   if(e[i].to != fa)
	     dfs(e[i].to, u, dep + 1), size[u] += size[e[i].to];
	}
	f[1] += w[u] * dep;
}
void dp(int u, int fa){  //转移
    for(int i = head[u]; i; i = e[i].next)
       if(e[i].to != fa)
         f[e[i].to] = f[u] + size[1] - size[e[i].to] * 2, dp(e[i].to, u);
    ans = min(ans, f[u]); //取最小值
}
int a, b;
int main(){
    //Open("hospital");
    ans *= ans;
    n = read();
    rep(i, 1, n){
       w[i] = read();
       a = read(); b = read();
       if(a) Add(i, a), Add(a, i);
       if(b) Add(i, b), Add(b, i);
    }
    dfs(1, 0, 0);
    dp(1, 0);
    printf("%lld\n", ans);
    //Close;
    return 0;
}

 

2.

用普通图的形式存储，

进行n遍bfs，然后每遍都进行答案的比较更新

###时间复杂度

由于bfs每遍都是O(V+E)的，而这里特殊之处在于本身是个树，所以是n个节点和n-1条边

所以总复杂度近似为O(n^2n2)，完美解决

——————————————————————————朴实的分割线——————————————————————————————

#include
#include
#include
#include
#include
using namespace std;
bool g[105][105]={0};            //这里n小我就直接邻接矩阵了，如果用邻接表还能快点 
bool v[105]={0};
int n,num[105],ans=1<<30;
struct node{
    int u,step;
};
int bfs(int x){                    //bfs找当前点x为医院设置点时的总距离 
    memset(v,0,sizeof(v));
    queue q;
    v[x]=1;
    q.push((node){x,0});
    int sum=0;
    while(!q.empty()){
        node now=q.front();
        q.pop();
        for(int i=1;i<=n;i++)
            if(g[now.u][i]&&!v[i]){
                node next={i,now.step+1};
                sum+=num[i]*next.step;
                v[i]=1;
                q.push(next);
            }
    }
    return sum;
}
int main(){
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        int a,l,r;
        scanf("%d%d%d",&a,&l,&r);
        num[i]=a;
        if(l) g[i][l]=g[l][i]=1;
        if(r) g[i][r]=g[r][i]=1;
    }
    for(int i=1;i<=n;i++)
        ans=min(ans,bfs(i));
    printf("%d",ans);
    return 0;
}

3.dp+floyd

#include
using namespace std;
int q[101];
int w[101][101];//w[i][j]为第i个节点到第j个节点的距离
int main() {
	int n,i,j,k,l,r,min,total;
	cin>>n;
	for(i=1; i<=n; i++) //记得在一开始把数据初始化 
	{
		for(j=1; j<=n; j++) {
			w[i][j]=1000000;
		}
	}
	for(i=1; i<=n; i++) //开始读入数据并将数据初始化 
	{
		w[i][i]=0;
		cin>>q[i]>>l>>r;
		if(l>0) w[i][l]=w[l][i]=1;
		if(r>0) w[i][r]=w[r][i]=1;
	}
	for(k=1; k<=n; k++) //开始dp+弗洛伊德算法，至于为什么要用dp+上弗洛伊德，打开算法标签，有动态规划。并且动态规划能更好的找出最小距离和 
	{
		for(i=1; i<=n; i++) {
			if(i!=k) {
				for(j=1; j<=n; j++) {
					if(i!=j&&k!=j&&w[i][k]+w[k][j]

 

希望大家喜欢！！！