图论——多源最短路Flody-Warshall算法

图论——多源最短路Flody-Warshall算法

Flody-Warshall算法

在本文中，我们使用一种不同的动态规划公式来解决所有节点对的最短路算法。称为Flody-Warshall算法。其运行时间为$O(V^3)$。

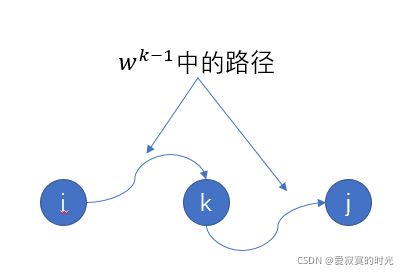
Flody-Warshall算法考虑的是某一条最短路上的中间节点。

设图$G$的节点集合为$V=\{1,2,\dots ,n\}$，令$V$的一个子集$V^k=\{1,2,\dots ,k\},k\le n$，设矩阵$w_{ij}^k$为所有满足以下下条件的路径中的最短路径：

• $i\to u\to j$中的中间节点$u\in V^k$。

那么全源最短路为$w^n$，下面说明如何由$w^{k-1}$推出$w^k$。

• 若节点$k$是满足中间节点是$k\in V^k$的$i\to j$最短路，那么最短路必然是$i\to k\to j$。那么由上述推断可知路径$i\to k$和$k\to j$都是中间节点为$V^{k-1}$的最短路，正好是$w^{k-1}$中的答案。

• 若节点$k$不是中间节点$V^k$中的最短路，则他必然是$V^{k-1}$中的最短路，因此两种情况取最小即可。

则有动态规划方程：

$$d_{ij}^k=\{\begin{array}{cc}{w}_{ij}& k=0\\ \min (d_{ij}^{k-1},d_{ik}^{k-1}+d_{kj}^{k-1})& k\ge 1\end{array}$$

其中$k=0$表示没有中间节点，那么就是初始图。

根据滚动数组的思想，我们并没有改变以后的状态，因此我们可以写出一下Flody算法的代码：

void flody(int n)
{
    for (int k = 1; k <= n; k++)         // 递推中间节点
        for (int i = 1; i <= n; i++)     // 初始节点
            for (int j = 1; j <= n; j++) // 结束节点
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}

例题

P1119

灾后重建，理解Flody的模板题目。我们将按照修建的顺序将节点进行排序，那么得到的顺序就是Flody算法中中间节点$k$更新的顺序。

传递闭包

另外Flody还能用来求传递闭包，传递闭包指在原图中若存在路径$i\to j$，那么在传递闭包图中$i$和$j$相邻。

我们只需要替换最小算子和加法算子为逻辑算子即可。

void flody(int n)
{
    for (int k = 1; k <= n; k++)         // 递推中间节点
        for (int i = 1; i <= n; i++)     // 初始节点
            for (int j = 1; j <= n; j++) // 结束节点
                d[i][j] = d[i][j] || d[i][k] && d[k][j];
}

消除传递闭包优化DAG上的DP

若在某种DAG的DP中，存在路径$i\to k\to j$比边$(i,j)$更优，那么边$(i,j)$是不必要的。

那么也就是说，在传递闭包中所有的传递路径都是不优的，我们在DP中根本不需要遍历这些边。

我们用下述算法优化DP：

1. 首先求出$G$的传递闭包$C$。
2. 枚举中点$k$，若$G[i][j]\wedge C[i][k]\wedge C[k][j]$，那么就令$G[i][j]=0$，即$i\to k$中存在带有中点的路径，那么$G[i][k]$就是无效边。

经过证明可知，一个完全DAG图经过上述优化之后边数$O(n^2)$最后优化为$O(n)$，即若有$n$个节点的DAG图，那么最终最多剩下$n-1$条边，即$1$到$n$的一个链。

2021CCPC for Female C

这个题就是经典的传递闭包优化DAG上的DP。

int own[40];
int w[40];
int G[40][40];
int C[40][40];
map<ll, int> dp[40];

void solve()
{
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        cin >> own[i];

    for (int i = 1; i <= n; i++)
        cin >> w[i];

    for (int i = 1; i <= m; i++)
    {
        int u, v;
        cin >> u >> v;
        G[u][v] = C[u][v] = 1;
    }

    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                C[i][j] = C[i][j] | C[i][k] & C[k][j];

    for (int k = 1; k <= n; k++)
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                if (G[i][j] && C[i][k] && C[k][j])
                    G[i][j] = 0;

    dp[1][ST(0, own[1])] = w[own[1]];
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++)
        {
            if (!G[i][j])
                continue;
            for (auto [stat, val] : dp[i])
            {
                if (!GT(stat, own[j]))
                {
                    dp[j][ST(stat, own[j])] = max(dp[j][ST(stat, own[j])], val + w[own[j]]);
                }
                else
                {
                    dp[j][stat] = max(dp[j][stat], val);
                }
            }
        }

    for (int i = 1; i <= n; i++)
    {
        int ans = 0;
        for (auto [stat, val] : dp[i])
        {
            ans = max(ans, val);
        }
        cout << ans << endl;
    }
}