【暑期每日一练】 day5

目录

 

选择题

（1）

解析 

（2）

解析 

（3）

解析 

（4）

解析

（5）

解析

编程题

题一

描述

示例

解析 

代码实现 

题二

描述

示例

提示

解析

代码实现

总结

---

 

选择题

（1）

1、如下程序的功能是（ ）

#include 
int main()
{
    char ch[80] = "123abcdEFG*&";
    int j;
    puts(ch);
    for(j = 0; ch[j] != '\0'; j++)
        if(ch[j] >= 'A' && ch[j] <= 'Z')
            ch[j] = ch[j] + 'e' - 'E';
    puts(ch);
    return 0;
}

A: 测字符数组ch的长度
B: 将数字字符串ch转换成十进制数
C: 将字符数组ch中的小写字母转换成大写
D: 将字符数组ch中的大写字母转换成小写
答案： D

解析 

一个字母对应的大写和小写之间的ASCII码值相差32，而且小写的大于大写的。所以题中'e'和'E'之间的ASCII码值相差，32（ch[j]+'e'-'E'相当于ch[j]+32）。一个字母从大写转化为小写就是在它自身上+32，小写转大写则是-32

（2）

2、对于代码段，下面描述正确的是（ ）

t=0;
while(printf("*"))
{
    t++;
    if (t<3)
        break;
}

A: 其中循环控制表达式与0等价

B: 其中循环控制表达式与'0'等价
C: 其中循环控制表达式是不合法的

D: 以上说法都不对

答案： B

解析 

因print(“*”)函数调用的返回值是字符串中字符的个数，即为1。所以while后面的条件恒为真，所以循环控制表达式与'0'是等价的（字符'0'不是0）。正确答案是B

（3）

3、以下程序运行时，若输入 1abcedf2df<回车> 输出结果是（ ）

#include 
int main()
{
    char ch;
    while ((ch = getchar()) != '\n')
    {
        if (ch % 2 != 0 && (ch >= 'a' && ch <= 'z'))
            ch = ch - 'a' + 'A';
        putchar(ch);
    }
    printf("\n");
    return 0;
}

A: 1abcedf2df B: 1ABCEDF2DF C: 1AbCEdf2df D: 1aBceDF2DF
答案： C

解析 

程序首先考虑ch的ASCII码值是不是奇数，再看是不是小写字母，同时满足时被改为大写字母

（4）

4、下列条件语句中，功能与其他语句不同的是（ ）

A: if(a) printf("%d\n",x); else printf("%d\n",y);
B: if(a==0) printf("%d\n",y); else printf("%d\n",x);
C: if (a!=0) printf("%d\n",x); else printf("%d\n",y);
D: if(a==0) printf("%d\n",x); else printf("%d\n",y);
答案：D

解析

D选项与众不同，其他都是a==0时输出y，a!=0时输出x

（5）

5、我们知道C语言的 break 语句只能跳出离它最近的一层循环，可是有时候我们需要跳出多层循环，下列跳出多层循环的做法正确的是【多选】（ ）

A: 将程序写成函数用return结束函数，便可跳出循环
B: 修改外层循环条件例如

for( int i = 0 ; i < MAX1 ; i ++ )
{
    for( int j = 0 ; j < MAX2 ; j ++ )
    {
        if( condition )
        {
            i = MAX1;
            break;
        }
    }
}

C: 在外层循环设置判断条件例如
 

for( ; symbol != 1 && condition2 ; )
{
    for( ; symbol != 1 && condition3 ; )
    {
        if( condition1 )
    symbol = 1 ;
    }
}

D: 在外层循环后面加入break例如
 

for( ; condition2 ; )
{
    for( ; condition3 ; )
    {
        if( condition1 )
        symbol = 1 ;
    } 
    if(symbol == 1 )
    break ;
}

答案：A、B、C、D

解析

此题旨在整理跳出多层循环的方法，每个选项都是正确的，代码为伪代码，condition代表逻辑表达式

编程题

题一

描述

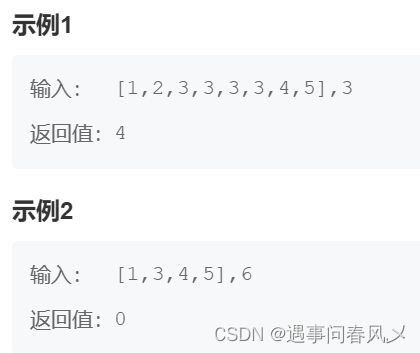
给定一个长度为 n 的非降序数组和一个非负数整数 k ，要求统计 k 在数组中出现的次数

数据范围：0≤k≤100，数组中每个元素的值满足 0≤≤val≤100

示例

解析 

采用遍历也能搞定，不过数组为非降序，采用二分查找的思想最优，先二分找到最左边的数字位置，再二分查找最右边的数字位置，两个位置相减+1就是长度了
中间比找的值大：则要找的数字肯定在右边， left = mid + 1;
中间比找的值小：则要找的数字肯定在左边， right = mid - 1；
中间值与找的值相同：
找的最左边数字：如果mid就是left，则返回mid就行，否则重置right=mid-1，把中心不断向左偏移
找的最右边数字：如果mid就是right，则返回mid就行，否则重置left=mid+1，把中心不断向右偏移

代码实现 

int get_last_or_first_idx(int* data, int len, int k, int flag) {//flag:0-找左边， 1-找右边
	int left = 0, right = len - 1, mid;
	while (left <= right) {
		mid = left + (right - left) / 2;
		if (data[mid] > k)
			right = mid - 1;
		else if (data[mid] < k)
			left = mid + 1;
		else {
			if (flag == 0) {//flag==0时，找最左边的数字
				if (mid == left || data[mid - 1] != k) return mid;
				else right = mid - 1;//把中心向左推
			}
			else {//flag==1时，找最右边的数字
				if (mid == right || data[mid + 1] != k) return mid;
				else left = mid + 1;//把中心向右推
			}
		}
	} 
	return - 1;
} int GetNumberOfK(int* data, int dataLen, int k) {
	if (dataLen == 0) return 0;
	int left = get_last_or_first_idx(data, dataLen, k, 0);
	int right = get_last_or_first_idx(data, dataLen, k, 1);
	if (left == -1 && right == -1) return 0; //表示没有找到k这个数据
	return right - left + 1;
}

题二

描述

整数转换。编写一个函数，确定需要改变几个位才能将整数A转成整数B。

示例

提示

A，B范围在[-2147483648, 2147483647]之间

解析

其实问需要修改多少个比特位，问的就是有多少个比特位不同而已，因为有多少位不同就修改多少位

代码实现

int get_bin_count(int num) {
	int count = 0;
	for (int i = 0; i < 32; i++) {
		if ((num >> i) & 1)
			count++;
	} 
	return count;
} 
int convertInteger(int A, int B) {
	return get_bin_count(A ^ B);
}

总结

关于今日练习讲解到这儿，欢迎各位留言交流以及批评指正，如果文章对您有帮助或者觉得作者写的还不错可以点一下关注，点赞，收藏支持一下。