四章：Constrained-CNN losses for weakly supervised segmentation——弱监督分割的约束CNN损失函数

0.摘要

        基于部分标记图像或图像标签的弱监督学习目前在CNN分割中引起了极大关注，因为它可以减轻对完整和繁琐的像素/体素注释的需求。通过对网络输出施加高阶（全局）不等式约束（例如，约束目标区域的大小），可以利用未标记数据，以领域特定知识指导训练过程。不等式约束非常灵活，因为它们不需要准确的先验知识。然而，出于计算可行性的原因，深度网络中很大程度上避免了受约束的拉格朗日对偶优化。据我们所知，Pathak等人（2015a）的方法是唯一一项在弱监督分割中处理带有线性约束的深度CNN的先前工作。它利用约束从弱标签中合成完全标记的训练掩码（提议），模仿完全监督并促进对偶优化。我们提出引入可微分的惩罚项，直接在损失函数中施加不等式约束，避免了昂贵的拉格朗日对偶迭代和提议生成。从受约束优化的角度来看，我们简单的基于惩罚的方法并不是最优的，因为不能保证约束条件被满足。然而，令人惊讶的是，它比Pathak等人（2015a）的基于拉格朗日的约束CNN方法取得了更好的结果，同时减少了训练的计算需求。通过仅对一小部分像素进行注释，所提出的方法可以达到与三个独立任务的完全监督相媲美的分割性能水平。虽然我们的实验集中在基本的线性约束，如目标区域大小和图像标签上，但我们的框架可以轻松扩展到其他非线性约束，例如不变形状矩（Klodt和Cremers，2011）和其他区域统计量（Lim等，2014）。因此，它有潜力弥合弱监督和完全监督学习在语义医学图像分割中的差距。我们的代码已公开提供。

1.引言

        近年来，深度卷积神经网络（CNN）在计算机视觉和医学成像中主导了语义分割问题，在有完全监督的情况下取得了突破性的性能（Long等，2015; Dolz等，2018; Litjens等，2017）。在语义分割中，完全监督需要繁琐的像素/体素注释，在许多应用中可能无法获得，尤其是处理体积数据时。此外，像素/体素级别的注释对于将深度分割网络扩展到新的对象类别或目标领域构成了严重的障碍。

        为了减轻像素级注释的负担，弱监督方法以部分或不确定的标签形式出现，例如边界框(Dai等人，2015年)，点(Bearman等人，2016年)，涂鸦(Lin等人，2016年；Tang等人，2018a年)或图像标签(Pinheiro和Collobert，2015年；Wei等人，2017年)，引起了重要的研究关注。在机器学习中，通过无监督损失项对网络的输出施加先验知识是一种成熟的方法(Weston等人，2012年；Goodfellow等人，2016年)。这些先验可以被视为利用未标记数据的正则化项，嵌入特定领域的知识。例如，Tang等人最近的研究表明，直接的正则化损失，如密集条件随机场(CRF)或成对聚类，可以在弱监督分割中取得出色的结果，在自然图像分割中几乎达到全监督性能。令人惊讶的是，在弱监督分割中，这种基于直接损失的方法并不常见。事实上，大多数现有技术从可用的部分标签中合成全标记的训练掩码(提议)，模拟全监督(Rajchl等人，2017年；Papandreou等人，2015年；Lin等人，2016年；Kolesnikov和Lampert，2016年)。通常，这种基于提议的技术迭代两个步骤：CNN学习和由密集CRF和快速平均场推理(Krähenbühl和Koltun，2011年)促进的提议生成，这现在已成为语义分割算法中成对正则化的事实选择。

        我们在这里的目的是直接将高阶（全局）不等式约束嵌入到损失函数中，以指导学习。例如，假设我们对目标区域的大小（或体积）有一些先验知识，例如在大小上的下界和上界，这在医学图像分割中是常见的情况（Niethammer和Zach，2013年；Gorelick等人，2013年）。设I：Ω⊂R2,3→R表示给定的训练图像，其中Ω是一个离散的图像域，|Ω|表示图像中的像素/体素数量。L⊆Ω是图像的弱（部分）真实分割，采用对目标区域的部分注释的形式，例如一些点（见图2）。在这种情况下，可以在网络输出上优化一个部分交叉熵损失，以满足不等式约束（Pathak等人，2015a年）：

        其中，S = (S1，...，S|Ω|) ∈ [0,1]|Ω| 是网络在每个像素 p 处生成的 softmax 概率向量，H(S) = -∑p∈ΩL log(Sp)。先验 a 和 b 表示目标区域大小（或基数）的给定上界和下界。式（1）中的不等式约束非常灵活，因为它们不需要对目标大小的精确知识，不像（Zhang等人，2017年；Boykov等人，2015年；Jia等人，2017年）。此外，多实例学习（MIL）约束（Pathak等人，2015a年），用于强制执行图像标签先验，可以通过受约束模型（1）来处理。图像标签是一种弱监督形式，用于强制执行目标区域在给定训练图像中存在或不存在的约束（Pathak等人，2015a年）。它们可以被视为（1）中不等式约束的特殊情况。例如，一个压制约束，形式为∑p∈ΩSp ≤ 0，强制目标区域不在图像中。∑p∈ΩSp ≥ 1 则强制目标区域出现在图像中。

        虽然式（1）中的约束对于网络输出是线性的（因此是凸的），但由于CNN的非凸性，受约束问题（1）非常具有挑战性。一种可能性是最小化相应的拉格朗日对偶问题。然而，正如（Pathak等人，2015a年；Márquez-Neila等人，2017年）所指出的，对于涉及数百万个参数的语义分割网络来说，这在计算上是难以处理的；必须在每个对偶迭代中优化CNN。事实上，在深度网络中，约束优化大部分被避免使用（Ravi等人，2018年），尽管在深度学习时代之前，一些拉格朗日技术被应用于神经网络（Zhang和Constantinides，1992年；Platt和Barr，1988年）。这些受约束优化技术对于深度CNN并不适用，因为它们解决了大规模线性方程组。在深度网络的情况下，这些受约束技术的数值求解器将不得不处理非常大维度的矩阵（Márquez-Neila等人，2017年）。

        据我们所知，Pathak等人（2015a年）的方法是唯一一个处理深度弱监督CNN分割中不等式约束的先前工作。它利用这些约束从现有的部分标签中合成完全标记的训练掩码（提议），模拟完全监督，避免了在最小化损失函数时约束的对偶优化问题。Pathak等人（2015a年）的主要思想是通过潜在分布对提议建模，然后最小化KL散度，尽可能地使CNN的softmax输出与潜在分布相匹配。因此，他们对潜在分布施加约束，而不是对网络输出施加约束，这有利于拉格朗日对偶优化。这种方法将网络参数的随机梯度下降学习和约束优化解耦：Pathak等人（2015a年）的作者在优化潜在分布方面进行交替，这对应于在约束条件下生成提议，同时使用标准的随机梯度下降优化网络参数。

        我们提出引入一个可微的项，直接在损失函数中强制执行不等式约束（1），避免了昂贵的拉格朗日对偶迭代和提议生成。从约束优化的角度来看，我们的简单方法并不是最优的，因为不能保证约束得到满足。然而，令人惊讶的是，与Pathak等人（2015a年）基于拉格朗日的约束CNN相比，我们的方法取得了明显更好的结果，同时减少了训练的计算需求。在心脏图像分割的背景下，我们使用了部分地面真值标签的一小部分（0.1%），达到了接近完全监督的性能。我们的框架可以轻松扩展到非线性不等式约束，例如不变形状矩（Klodt和Cremers，2011年）或其他区域统计量（Lim等人，2014年）。因此，它有潜力在语义医学图像分割中弥合弱监督学习和完全监督学习之间的差距。我们的代码公开可用。

2.相关工作

2.1.语义图像分割的弱监督方法

        使用部分和/或不确定注释训练分割模型是一个具有挑战性的问题（Vezhnevets等人，2011年；Buhmann等人，2012年）。由于提供关于图像中对象存在与否的全局图像级信息相对容易，许多弱监督方法使用图像标签来学习分割模型（Verbeek和Triggs，2007年；Vezhnevets和Buhmann，2010年）。例如，在Verbeek和Triggs（2007年）中，通过图像级关键词学习了一个概率潜在语义分析（PLSA）模型。然后，该模型被用作马尔可夫随机场（MRF）中的一元势函数，用于捕捉邻居之间的二维空间关系。此外，由于经典交互式分割方法（如非常流行的GrabCut（Rother等人，2004年））的广泛使用，边界框成为一种非常流行的弱标注形式。该方法学习了两个高斯混合模型（GMM），用于对边界框定义的前景和背景区域建模。为了对图像进行分割，外观和平滑性被编码在一个二元MRF中，通过图割可以进行精确推断，因为能量是次模的。另一种常见的弱监督形式是使用涂鸦，可以由注释者交互地进行，以纠正分割结果。

        GrabCut是在深度学习时代之前使用弱监督进行“浅层”交互式分割的众多著名示例之一。最近，在计算机视觉社区中，人们对利用弱标注来训练深度CNN进行彩色图像分割产生了很大兴趣，例如使用图像标签（Pathak等人，2015a；2015b；Xu等人，2014；Papandreou等人，2015；Pinheiro和Collobert，2015；Wei等人，2017）、边界框（Dai等人，2015；Rajchl等人，2017；Khoreva等人，2017）、涂鸦（Xu等人，2015；Lin等人，2016；Vernaza和Chandraker，2017；Tang等人，2018b；2018a）或者点（Bearman等人，2016）。这些弱监督的语义分割技术中，大部分都通过生成完整的训练掩码（分割建议）来模仿完全监督。这些建议可以看作是用于训练CNN的合成的“真实标签”。一般而言，这些技术遵循一个迭代的过程，交替进行两个步骤：（1）使用建议训练CNN的标准随机梯度下降；（2）基于标准正则化的分割，生成建议。第二步通常使用标准的优化器，如均场推断（Papandreou等人，2015；Rajchl等人，2017）或者图割（Lin等人，2016）。特别是，Krähenbühl和Koltun（2011）的密集CRF正则化器，在快速并行均场推断的支持下，在语义分割中变得非常流行，无论是在完全监督（Arnab等人，2018；Chen等人，2015）还是弱监督（Papandreou等人，2015；Rajchl等人，2017）的设置中。这得益于DeepLab（Chen等人，2015）的巨大成功，它在完全监督的CNN分割中推广了密集CRF和均场推断作为后处理步骤的使用。

        这些提议策略的一个重要缺点是它们对提议中的错误非常敏感，在这种自学习方案中可能会加强这些错误，从而破坏了收敛保证（Chapelle等人，2006）。Tang等人最近的方法（2018b，a）将密集CRF或成对图聚类等标准正则化器直接集成到损失函数中，避免了额外的推理步骤或提议生成。这种直接的正则化损失在弱监督颜色分割中取得了最先进的性能，接近于完全监督的准确性。虽然这些方法在训练过程中鼓励像素之间的成对一致性，但它们并没有像（1）中那样明确地施加全局约束。

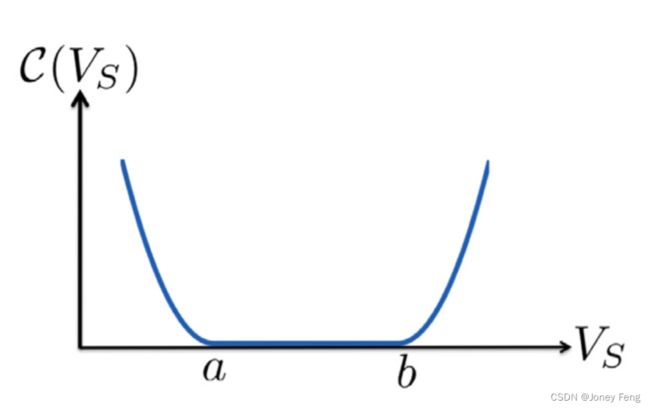
图1. 我们的可微损失函数对目标区域施加软尺寸约束的示意图。

2.2.使用弱监督的医学图像分割

        尽管越来越多的工作集中在弱监督深度CNN在彩色图像语义分割中的应用上，但在医学图像设置中利用弱标注并不简单。据我们了解，关于这个问题的文献仍然很少，这使得弱监督方法在医学图像分割中具有吸引力。与彩色图像类似，常见的弱标注设置是边界框。例如，DeepCut（Rajchl等人，2017）采用了类似于Papandreou等人（2015）的设置。它生成图像提议，并在重新用于训练CNN之前通过密集CRF进行了精炼，作为“虚假”标签。作者通过将边界框作为Grab-cut算法的初始化，展示了通过这种迭代优化方案可以获得比浅层方法（即GrabCut）更好的性能。在另一个弱监督场景中（Rajchl等人，2016），图像以无监督的方式进行分割，生成一组超像素（Achanta等人，2012），用户必须从中选择属于感兴趣对象的区域。然后，从超像素生成的这些掩码被用于训练CNN。然而，由于这些提议是以无监督的方式生成的，并且由于医学图像通常具有较差的对比度和具有挑战性的目标，这些“虚假”标签很可能容易出现错误，在训练过程中可能会传播，如前面所述。

2.3.约束CNNs

        据我们所知，只有最近的几项研究（Pathak等人，2015a；Márquez-Neila等人，2017；Jia等人，2017）涉及对深度CNN施加全局约束。实际上，在涉及数百万个参数的现代深度网络中，标准的拉格朗日对偶优化已经完全被避免使用。正如最近在（Pathak等人，2015a；Márquez-Neila等人，2017）中指出的，社区内普遍认为，在现代计算机视觉和医学图像分析问题中，对深度CNN的输出施加约束是不切实际的：直接使用拉格朗日对偶优化对于具有数百万个参数的网络来说，需要在每次迭代的对偶步骤之后训练整个CNN（Pathak等人，2015a）。为了避免计算上难以处理的对偶优化问题，Pathak等人（2015a）对潜在分布施加了不等式约束，而不是对网络输出施加约束。这个潜在分布描述了一个“虚假”的真实值（或分割提议）。然后，他们训练了一个单一的CNN，以最小化网络概率输出和潜在分布之间的KL散度。这个先前的工作与我们的研究最相关，并且据我们所知，是唯一一个在弱监督CNN分割中解决不等式约束的工作。Márquez-Neila等人（2017）的工作则对3D人体姿态估计施加了严格的等式约束。为了解决计算困难，他们使用了基洛夫子空间方法，并将求解器限制在每次迭代中仅选择一组随机选择的子集约束中。因此，在一次迭代中满足的约束可能在下一次迭代中不满足，这可能解释了（Márquez-Neila等人，2017）中的负面结果。在（Márquez-Neila等人，2017）中一个令人惊讶的结果是，用简单的L2惩罚替代等式约束比拉格朗日优化得到更好的结果，尽管这样一个简单的基于惩罚的公式并不能保证约束满足。在Jia等人（2017）中也使用了类似的L2惩罚，在组织病理学分割的背景下对目标区域的大小施加了等式约束。虽然（Márquez-Neila等人，2017；Jia等人，2017）中的等式约束公式非常有趣，但它们假设对目标函数（例如区域大小）具有精确的知识，不像（1）中的不等式约束公式那样，它允许更多关于所需先验领域特定知识的灵活性。

3.提出的损失函数

 

         其中 ∂Sp / ∂θ 表示网络的softmax输出的标准导数。(4)中的梯度有一个明确的解释。在反向传播过程中，当当前的约束被满足时，即 a ≤ VS ≤ b，观察到 ∂C / ∂(θVS) = 0。因此，在这种情况下，我们项产生的梯度对当前网络参数的更新没有影响。现在，假设不失一般性，当前的参数集 θ 对应于 VS < a，这意味着当前的目标区域小于其下界 a。在这种违反约束的情况下，项 (a - VS) 是正的，因此 (4)中的第一行对softmax输出进行梯度上升步骤，增加 Sp。这是有道理的，因为它增加了当前区域 VS 的大小，以满足约束。当 VS > b 时，有类似的解释。下一节详细介绍了数据集、弱标注和我们的实现。然后，我们对我们的约束-CNN损失对分割性能的影响进行全面评估。我们还将与Pathak等人（2015a）的基于拉格朗日的约束CNN方法以及完全监督设置进行比较。

4.实验

4.1.医学图像数据

        在本节中，我们对提出的损失函数在三个公开可用的数据集上进行了评估，每个数据集对应于不同的应用领域——心脏、椎体和前列腺分割。以下是这些数据集的详细信息。

4.1.1.在心脏连续磁共振成像（cine MRI）中的左心室（LV）

        我们的实验重点是左心室内膜分割。我们使用了2017年ACDC挑战赛公开可用的训练集。该数据集包含了100个心脏磁共振（MR）检查，涵盖了定义明确的病理：扩张型心肌病、肥厚型心肌病、心肌梗死伴左室射血分数改变和异常右室。还包括正常受试者。每个检查仅包含舒张期和收缩期的图像。这些检查是在屏气情况下进行的，采用了顾及或预测性门控和2腔室、4腔室和短轴方向的SSFP序列。一系列短轴切片从基底到顶部覆盖了左心室，厚度为5-8毫米，间隔为5毫米。空间分辨率从0.83到1.75 mm2/像素不等。对于所有实验，我们使用相同的75个检查进行训练，剩下的25个用于验证。

4.1.2.在MR-T2图像上的椎体（VB）

        该数据集包含了23个患者的23个3D T2加权快速自旋回波磁共振图像及其相关的地面真值分割，可以免费获取。每个患者使用1.5特斯拉磁共振成像仪（西门子医疗，德国埃朗根）进行扫描，生成T2加权矢状位图像。所有图像的采样大小为39×305×305个体素，体素间距为2×1.25×1.25 mm³。在每个图像中，手动识别和分割了T11到L5的7个椎体，总共得到161个标记区域。对于这个数据集，我们使用了15个扫描进行训练，剩下的5个用于验证。

4.1.3.在MR-T2图像上的前列腺分割

        第三个数据集是在MICCAI 2012前列腺MR分割挑战赛中提供的。它包含了50名患者的经过横断面T2加权MR图像，这些图像在不同的中心使用多个MRI供应商和不同的扫描协议进行获取。该数据集包括各种疾病，例如良性和前列腺癌。图像的分辨率范围从15×256×256到54×512×512个体素，体素间距范围从2×0.27×0.27到4×0.75×0.75 mm³。我们使用了40名患者进行训练，剩下的10名用于验证。

4.2.弱标注

        为了证明所提出的方法对生成弱标签的策略以及其位置的鲁棒性，我们考虑了两种不同的策略，从完全标记的图像中生成弱标注。图2展示了一些完全标注图像和相应的弱标签的示例。

1. 腐蚀法：对于左心室数据集，我们对完全标注进行了二值腐蚀操作，使用大小为10×10的卷积核。如果结果标签消失，我们会使用较小的卷积核（例如7×7）再次进行操作，直到得到一个小的轮廓。因此，弱标注的总像素数相当于完全监督场景中标记像素的0.1%。这对应于图2中的第二行。
2. 随机点法：对于椎体和前列腺数据集，我们通过在地面真值掩膜内随机选择一个点，并在该点周围创建一个最大半径为4个像素的圆来生成弱标签（图2中的第四行和第六行），同时确保与背景没有重叠。通过这些弱标注，数据集中只有0.02%的像素具有地面真值标签。

4.3.不同层次的监督

        使用不同级别的监督来训练具有多样性的模型需要为每种情况定义适当的目标。在本节中，我们介绍了不同的模型，每个模型都具有不同级别的监督。

4.3.1.基准线

        我们从弱标注图像训练了一个分割网络，没有额外的信息，这作为一个较低的基准线。训练这个模型依赖于最小化与标记像素比例对应的交叉熵：H(S) = - ∑p∈L log(Sp)。在接下来的实验讨论中，我们将这个模型称为部分交叉熵（CE）。作为一个较高的基准线，我们采用完全监督的设置，在训练过程中对每个像素都知道类别标签（前景和背景）（L = ）。这个模型被称为完全监督。

4.3.2.尺寸约束

        我们在训练过程中引入了关于目标区域大小的信息，并在满足不等式约束条件的情况下优化部分交叉熵损失，其一般形式如公式（1）所示。我们使用相同的弱标注图像训练了几个模型，但使用不同的约束值。图像标签范围。类似于多示例学习场景，我们首先使用图像标签先验知识，通过强制要求在给定的训练图像中存在或不存在目标来进行训练，正如之前介绍的那样。这相当于强制要求如果图像中没有目标，则预测区域的大小小于等于0，否则大于0。为了简化实现，我们可以将约束表示为：

         尽管非常粗糙，但这些约束传达了有关目标区域的相关信息，可以用于在区域缺失或存在的情况下找到共同的模式。常见的约束。下一级的监督包括对正例使用更紧密的界限，而不是使用（1，|L|）。为此，使用单个患者的完整分割结果来计算在所有切片中目标区域的最小和最大大小。然后，我们将这些最小和最大值分别乘以0.9和1.1，以考虑患者之间的变异性。在这种情况下，包含感兴趣对象的所有图像具有相同的下界和上界。以ACDC数据集为例，结果如下：

 

        其中Y = (Y1,...,Y|L|)∈{0,1}|L|表示图像I的完整注释。与之前一样，我们对目标大小引入一些不确定性，并将τY乘以相同的下界和上界因子，得到以下界限：

 

 图2.不同监督级别的示例。在完全标记的图像（顶部），所有像素都被注释，红色表示背景，绿色表示感兴趣区域。在弱监督的情况下（底部），只知道绿色像素的标签。为了更好地显示弱标签，图像被裁剪了。原始图像的尺寸为256×256像素。（对于该图例中颜色的解释，请参考本文的网络版本。）

4.3.3.混合训练

        我们还研究了在训练过程中将我们提出的弱监督方法与完全注释的图像相结合是否会提高性能。为此，考虑到我们有m个弱标注的图像的训练集，我们将其中的n个（n < m）替换为完全注释的对应图像。因此，训练过程包括对n个完全注释的图像进行交叉熵损失的最小化，以及对其余m-n个弱标注图像进行部分交叉熵与常见大小约束的最小化。为了检验在这种情况下尺寸约束的积极效果（称为混合模型），我们将结果与仅使用n个完全注释图像训练的网络（无约束）进行比较。

4.4.约束一个三维体积

4.5.训练和实现细节

        在左心室和椎体数据集的实验中，我们使用了ENet（Paszke等人，2016），因为它在准确性和推断时间之间取得了良好的平衡。由于前列腺分割任务的难度较高，我们使用了类似于Quan等人（2016）的完全残差版本的U-Net（Ronneberger等人，2015）。

        对于这三个数据集，我们使用Adam优化器从头开始训练网络，并使用初始学习率为5×10^-4，如果在验证集上的性能在20个epoch内没有改善，我们将学习率减小为原来的一半。所有的3D体积都被切割成256×256像素的图像，并在需要时进行零填充。左心室、前列腺和椎体的批处理大小分别为1、4和20。这些值没有针对最佳性能进行调整，而是为了在有足够数据的情况下加快实验速度。我们在公式（2）中的损失权重经验性地设置为1×10^-2。由于任务的难度，我们对前列腺数据集使用了数据增强，通过随机镜像、翻转和旋转生成每个训练图像的4个副本。

我们所有的测试都是在Pytorch（Paszke等人，2017）中实现的。我们在一台配备了NVIDIA GTX 1080 Ti GPU（11GB的视频内存）、AMD Ryzen 1700X CPU和32GB内存的机器上运行实验。代码可在GitHub - LIVIAETS/SizeLoss_WSS: Code of our MIDL 2018 paper and MedIA extension: https://arxiv.org/abs/1805.04628 上获取。我们使用常见的Dice相似系数（DSC）来评估训练模型的分割性能。

4.5.1.拉格朗日建议的修改和微调

        为了进行公平比较，我们在PyTorch中重新实现了Pathak等人（2015a）的拉格朗日提议方法，以充分利用GPU的能力并避免在GPU和CPU之间进行昂贵的数据传输。拉格朗日提议方法重复使用与完全监督设置相同的网络和损失函数。在每次迭代中，该方法在两个步骤之间交替进行。首先，使用双变量的投影梯度上升（PGA）合成一个带有投影梯度上升的伪标签Y，其中网络参数固定不变。然后，在固定Y的情况下，通过优化Y~和S之间的交叉熵来进行标准的完全监督CNN训练。我们经验性地将用于PGA的学习率设置为5×10^-5，因为次优的值会导致数值错误。我们发现将PGA的迭代次数限制为500（而不是原始的3000）可以节省时间而不影响结果。我们还在PGA中引入了一个早停机制，以提高速度而不影响结果（在表5中可以找到比较）。形式为0 VS 0的约束需要特别注意，因为（Pathak等人，2015a）的公式不是设计用于处理等式，而我们的惩罚方法在a = b时始终处理等式约束。在这种情况下，Pathak等人（2015a）的边界被修改为-1 VS 0。

5.结果

        为了验证我们提出的方法，我们首先进行了一系列关注左心室分割的实验。在第5.1节中，我们使用我们的直接惩罚方法评估了包含尺寸约束的影响。我们进一步与Pathak等人（2015a）的拉格朗日提议方法进行比较，结果显示我们的简单方法在相同的弱监督设置下比（Pathak等人，2015a）有显著的改进。我们还在第5.2节中提供了几种监督程度的结果，包括混合监督学习和完全监督学习。然后，为了展示所提出的约束损失的广泛适用性，我们在第5.3节中报告了另外两个应用的结果：MR-T2椎体分割和前列腺分割任务。我们在第5.4节中进一步提供了三个应用的定性结果。在第5.5节中，我们研究了所提出的损失对下界和上界的敏感性。最后，我们比较了不同学习策略的效率（第5.6节），结果显示我们的直接约束CNN损失不会增加训练时间，而Pathak等人（2015a）的拉格朗日提议方法会增加训练时间。

5.1.基于尺寸约束的弱监督分割

2D分割。表1报告了在左心室验证集上使用Pathak等人（2015a）的拉格朗日提议和我们的直接损失训练的所有模型的结果。如预期，使用部分交叉熵和部分标记像素的结果很差，平均DSC小于15%。像MIL情景中一样，强制执行图像标签约束显著提高了DSC值，达到0.7924。在这种情况下，使用常见的边界稍微提高了结果，平均Dice值增加了1%。拉格朗日提议（Pathak等人，2015a）达到了类似的结果，尽管稍低且不稳定得多，比我们的惩罚方法要差（见图3）。当我们使用单独的边界时，性能差异更为明显。在这种设置下，我们的方法的DSC为0.8708，仅比完全监督低2%。然而，拉格朗日提议方法的性能与使用常见（宽松）边界的性能相似，这表明它不能利用这些额外的、更精确的信息。这可以通过其提议生成方法来解释，该方法倾向于强化早期的错误（尤其是在从零开始训练时）：网络在训练过程中接收到冲突的信息，即根据合成的伪标签，相似的图像块既是前景又是背景，并且无法从这些初始错误分类中恢复。

3D分割。对目标区域的3D体积大小进行约束也显示了我们的惩罚方法的好处，得到了平均DSC为0.8580的结果。需要注意的是，在这里，我们比2D情况下使用了更少的监督。由于在这种情况下我们不使用标签信息，这些结果表明在创建标签时可能只使用部分切片，使得标注者可以直接在3D图像上进行标记，而不需要逐个处理所有的2D切片。

表1.不同监督级别下的左心室分割结果。粗体字突出显示最佳的弱监督设置。

表2.关于完全标记和弱标记数据量的消融研究。我们报告了所有测试案例的平均DSC，对于所有设置都使用相同的架构。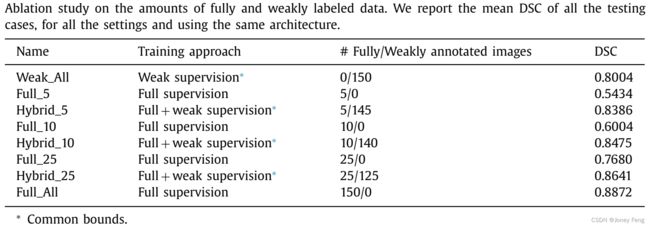

图3.在左心室验证集上进行训练期间DSC的演变，包括弱监督学习模型和不同策略的分析，以及完全监督的设置。由于标签和公共边界实现了类似的结果，我们只绘制公共边界以便更好地阅读。（对于该图例中颜色的解释，请参考本文的网络版本。）

5.2.混合训练：混合使用完全和弱标注的图像

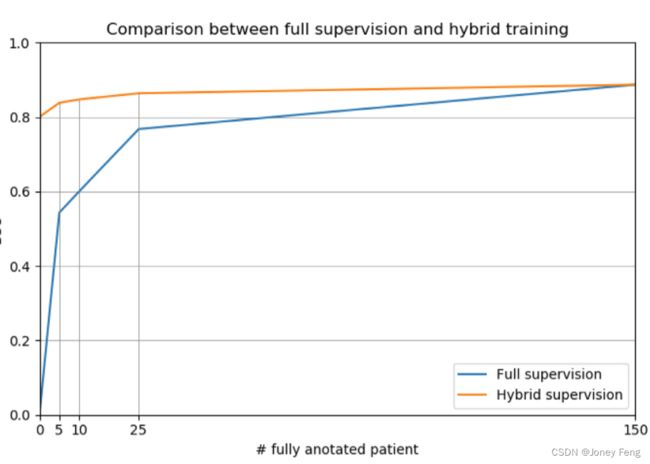
        表2和图4总结了在弱监督和完全监督相结合时获得的结果。首先，正如预期的那样，我们可以观察到将n个完全注释的图像添加到训练集（Hybrid_n）中相比仅使用弱标注图像训练的模型（即Weak_All）可以改善性能。特别地，当n分别等于5、10和25时，DSC值分别增加了4%、5%和6%，仅使用25%的完全标注图像就接近了完全监督的性能。

        然而，更有趣的是观察将弱标注图像（即Hybrid_n）添加到仅使用完全标注图像（即Full_n）训练的模型中的影响。从结果中我们可以观察到，将弱标注图像添加到训练集中显著提高了性能，尤其是当完全标注图像的数量（即n）有限时。例如，在n等于5的情况下，与n等于5的完全监督相比，添加弱标注图像使性能提高了30%以上。尽管这个差距随着完全标注图像的数量的增加而减小，但Full和Hybrid两种设置之间的差异仍然显著。更有趣的是，使用大量的弱标注图像和没有或非常少量的完全标注图像（例如Weak_All或Hybrid_5）训练相同的模型比使用完全标注图像数量更多的数据集（例如Full_25）获得更好的性能。这些结果表明，在注释新数据集时，一个好的策略可能是先为所有图像使用弱标签，并逐渐完成完全标注，一旦资源可用。

 图4.在用于训练的完全注释患者数量上的平均DSC值。（对于该图例中颜色的解释，请参考本文的网络版本。）

5.3.MR-T2锥体和前列腺分割

        对于椎体数据集的结果（表3），很好地突显了不同监督水平性能之间的差异。使用标签边界产生了一个大致定位感兴趣对象的网络（DSC为0.5597），但无法识别其边界（如图6第三列所示）。使用常见大小策略可以在包含具有规则形状的对象的切片上获得令人满意的结果，但在存在更困难/不规则目标的情况下仍然失败，导致DSC的整体改善（0.7900）。然而，当使用个体边界时，网络能够满意地分割甚至最困难的情况，获得DSC为0.8604，仅比完全监督低3%。对于前列腺数据集，我们可以观察到常见边界仍然改善了使用标签获得的结果（+3%），但与椎体分割的情况相比，差异要小得多。使用个体边界将DSC值提高了10%，达到0.8298，这与我们之前观察到的其他数据集的行为相似。然而，在这种情况下，完全监督和使用个体边界约束的弱监督之间的差距比我们在其他数据集中获得的要大。

5.4.定性结果

        为了对不同的学习策略及其对分割的影响有一定的直观认识，我们在图5-7中分别对LV、VB和前列腺的验证集中抽取了一些结果进行可视化。LV分割任务。我们将4种方法与基准结果进行比较：完全监督、Lagrangian proposals（Pathak et al.,2015a）采用常见边界、直接损失采用常见边界和直接损失采用个体边界。我们可以看到，在包含规则形状和可见边界的简单情况下，所有方法都获得了类似的结果。然而，使用常见边界的方法在物体较小的情况下很容易过度分割，例如图5中的最后一行。由于个体边界是针对每个图像具体的，使用这些边界训练的模型在这种情况下不会受到影响，正如图中所示。

椎体分割任务。在这种情况下，我们可视化了完全监督、标签边界、常见边界和个体边界的结果。与表3中报告的结果一致，我们可以在视觉上观察到每个设置之间性能差异的差距，这清楚地突显了优化过程中边界不同值的影响。当仅使用标签时，网络学习到了大致定位对象的能力。当将大小边界作为常见大小信息包含在内时，网络能够在某种程度上学习到边界，但仅适用于典型椎体形状的标准变异范围内的对象形状。正如可以观察到的，模型无法对不寻常的形状进行分割（图6中的最后三行）。最后，使用个体大小训练的网络能够更好地处理这些情况，但在某些区域仍不够精确。

前列腺分割任务。与前面的情况类似，我们展示了完全监督、标签边界、常见边界和个体边界的结果。标签和常见边界都以类似的方式定位对象，但都难以找到精确的轮廓，通常会过度分割目标区域。这可以很容易地解释为器官的变异性以及某些图像上非常低的对比度。如最后一列所示，使用个体边界极大地改善了结果。

表3.使用脊椎体和前列腺验证集，对于几种监督程度的平均Dice分数（DSC）。粗体字表示每个数据集的最佳弱监督设置。

 图5.使用LV数据集的示例进行不同方法的定性比较。每列显示了不同方法得到的分割结果，而每行表示来自不同扫描的2D切片（最佳以彩色视图查看）。 （对于该图例中颜色的解释，请参考本文的网络版本。）

图6.使用VB数据集的示例进行定性比较。每列显示了不同监督水平下得到的分割结果，而每行表示来自不同扫描的2D切片（最佳以彩色视图查看）。 （对于该图例中颜色的解释，请参考本文的网络版本。）

5.5.对约束边界的敏感性

        在本节中，对常见边界的下限和上限进行了割脱研究，并研究了它们对椎体分割任务性能的影响。不同边界的结果如表4所示。可以观察到，逐渐增加上限值会降低性能。例如，当上限增加5倍和10倍时，DSC下降了近12%和16%。将下限从80降低到0对性能的影响要小得多，保持在不到1%的恒定下降。这些发现与图6中的视觉预测一致。当仅使用标签边界训练的网络倾向于过度分割时，添加上限边界可以很容易地修复过度分割，纠正大部分错误。然而，出于同样的原因，即过度分割，很少有切片受益于下限边界。

图7.对不同监督水平进行定性比较。每行表示来自不同扫描的2D切片。（最佳以彩色视图查看）。（对于该图例中颜色的解释，请参考本文的网络版本。）

表4.使用脊椎体数据集对尺寸约束的下限和上限进行剔除研究。

表5.使用批量大小为1的标签和大小约束，对不同监督学习策略进行训练所需的时间。

5.6.效率

        在本节中，我们根据效率（表5）对几种学习方法进行了比较。无论是弱监督的部分交叉熵还是完全监督的模型，每次传递只需要计算一次损失。这反映在表中报告的最低训练时间中。如结果所示，包括大小损失并不会增加计算时间。正如Pathak等人（2015a）在每次前向传递中引入的迭代过程所预期的那样，在训练过程中会添加显著的开销。为了生成他们的合成真值，他们需要相对于其对偶变量（约束的拉格朗日乘子）优化拉格朗日函数，这需要在训练CNN和拉格朗日对偶优化之间交替进行。即使在最简单的优化情况下（只有一个约束），在双重变量优化收敛迅速的情况下，他们的方法仍比我们的方法慢两倍。如果没有我们引入的早停准则，开销将增加六倍，更是糟糕得多。此外，当添加更多约束时，他们的方法也会变慢。当需要约束/监督的类别很多时，这一点尤其重要。在每次迭代中生成建议也使得为更大的批次大小构建高效实现变得更加困难。要么需要逐个生成它们（因此开销与批次大小线性增长），要么尝试并行执行。然而，由于GPU设计的性质，平行的拉格朗日优化会相互拖慢，这意味着顺序生成可能有限的改进。在某些情况下，使用CPU执行可能更快（其中核心可以真正并行执行独立任务），但这会导致GPU和CPU之间的传输速度变慢。最佳策略将取决于批次大小和主机机器，特别是其可用的GPU、CPU核心数量和总线频率。

6.讨论

        我们提出了一种在弱监督分割中使用线性约束来训练深度卷积神经网络的方法。为此，我们引入了一个可微的项，直接在损失函数中强制执行不等式约束，避免了昂贵的拉格朗日对偶迭代和提议生成。

        结果表明，利用提出的直接大小损失来利用弱标注数据的能力非常有益，特别是在有限的完全标注数据可用时。这可以通过以下事实来解释：当有大量完全标注的训练集可用时，网络已经被正确训练，这与表2中报告的数值一致。在（Bai等，2017年；Zhou等，2018年）中也报告了类似的发现，作者在半监督设置中包含非注释图像时性能提高。这表明，包含更多未标记或弱标记的数据可能会显著提高性能。

        跨不同分割任务的实验结果表明，通过对目标大小进行粗略估计，可以获得高竞争力的性能。这在问题结构良好的情况下尤为明显，其中对象的大小和/或形状在不同主体之间保持一致。如果提供更精确的大小边界，即使在不同主体之间的大小和形状变化很大的情况下，所提出的方法也能接近完全监督的性能。对于困难的任务，我们的方法与完全监督之间的差距较大，例如前列腺分割，包括无监督的正则化损失（Tang等，2018a；2018b）以鼓励像素之间的成对一致性可能会提高所提出策略的性能。值得注意的是，我们的方法对于弱标签的生成具有鲁棒性。虽然第一个数据集的弱标签是从地面实况侵蚀生成的，种子始终位于目标区域的中心，但其他两个数据集的弱标签是随机生成和放置的。因此，结果显示了不同方法的行为的一致性，不论使用的策略如何。尽管已经证明了所提出的方法可以提供

        尽管该方法在三个不同的应用中展示了良好的泛化能力，但对于具有严重异常的图像进行分割，其大小与训练集中的大小差异很大，尚未进行评估。然而，对尺寸边界的消融研究以及使用常见边界尺寸得到的结果表明，通过增加上限值，所提出的方法可能在存在这些严重异常的情况下仍能表现令人满意。此外，如果能更精确地估计异常的大小，我们提出的损失函数可能会改善分割性能，正如个别边界策略所取得的结果所示。值得注意的是，即使在完全监督的情况下，如果新的测试图像包含比训练阶段中见到的对象要大得多的严重异常，网络可能会对感兴趣区域进行较差的分割。

我们的框架可以很容易地扩展到其他非线性（分数）约束，例如不变形状矩（Klodt和Cremers，2011）或其他统计量，如目标区域内强度的均值（Lim等，2014）。例如，一个目标区域的归一化（尺度不变）形状矩可以直接用以下一般的分数形式来表示，其中网络输出的术语为：

        其中，fp是以像素/体素坐标的指数形式表示的一元势能。例如，目标区域质心的坐标是方程（8）的特殊情况，并对应于一阶尺度不变形状矩。在这种情况下，势能fp对应于像素坐标。现在，假设我们处于弱监督的情况下，我们对目标区域的质心有一个粗略的定位。在这种情况下，可以使用对质心的线索，而不是像方程（3）中的尺寸表示约束，如a × FS × b。这可以通过使用可微分的惩罚函数C(FS)来实现直接的损失。当然，在这里，FS是一个非线性的分数项，与区域尺寸不同。因此，在未来的工作中，值得研究这种分数项在使用惩罚方法约束深度卷积神经网络时的行为。最后，值得注意的是，方程（8）中的一般形式不仅适用于形状矩。例如，目标区域内的图像（强度）统计量，如均值，也遵循方程（8）中的相同一般形式。因此，类似的方法可以在我们对这些图像统计量有先验知识的情况下使用。

        我们基于惩罚的直接方法用于不等式约束，相对于拉格朗日对偶优化（Pathak等，2015a），在性能上取得了显著的提升，同时速度更快、更稳定。我们假设这部分原因是由于原始问题的随机优化（如随机梯度下降）和拉格朗日对偶的迭代/投影之间的相互作用。这些对偶的迭代/投影是处理约束的基本（非随机）梯度方法。基本梯度方法在深度网络中存在众所周知的问题，例如对学习率敏感，容易陷入弱局部最小值。因此，拉格朗日优化中的对偶部分可能会阻碍随机优化（如速度和强大的泛化性能）在无约束深度网络损失函数中的实际和理论好处，后者已经在研究中得到广泛确认（Hardt等，2016）。我们的基于惩罚的方法将约束问题转化为无约束损失，从而在随机优化中完全处理约束，并完全避免了对偶步骤的使用。尽管基于惩罚的方法不能保证约束的满足，但我们的工作表明，在约束CNN分割的背景下，它们可以非常有用。

7.总结

        本文提出了一种新颖的损失函数用于弱监督图像分割，尽管其简单性，但在这个任务中表现出比拉格朗日优化显著更好的性能。我们通过仅标注少量像素，在三个不同任务中实现了接近全监督的结果，并且计算开销几乎可以忽略不计。虽然我们的实验主要集中在基本的线性约束，如目标区域的尺寸和图像标签上，但我们的直接约束CNN损失函数可以很容易地扩展到其他非线性约束，例如不变形状矩（Klodt和Cremers，2011）或其他区域统计量（Lim等，2014）。因此，它有潜力在语义医学图像分割中弥合弱监督学习和全监督学习之间的差距。