树 - 前缀树(Trie Tree)
树 - 前缀树(Trie Tree)
- 什么是前缀树
- 前缀树的实现
-
- 节点数据结构定义
- 插入方法
-
- ●非递归方式
- ●递归方式
- 查询单词方法
-
- ●非递归方式
- ●递归方式
- 查询前缀方法
-
- ●非递归方式
- ●递归方式
- 前缀树的复杂度
- 前缀树有哪些应用
- 前缀树的压缩:基数树
- 双数组Trie树(DoubleArrayTrie)
- 参考文章
- LeetCode--208. 实现 Trie (前缀树)
- Trie,又称字典树、单词查找树或键树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来减少查询时间,最大限度地减少无谓的字符串比较,查询效率比哈希树高。
什么是前缀树
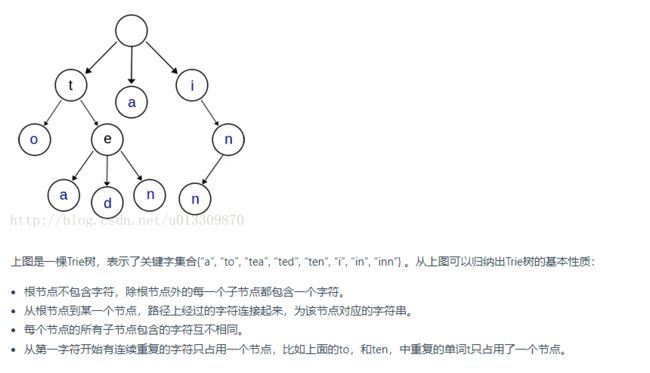
在计算机科学中,trie,又称前缀树或字典树,是一种有序树,用于保存关联数组,其中的键通常是字符串。与二叉查找树不同,键不是直接保存在节点中,而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀,也就是这个节点对应的字符串,而根节点对应空字符串。一般情况下,不是所有的节点都有对应的值,只有叶子节点和部分内部节点所对应的键才有相关的值。
Trie 这个术语来自于 retrieval。根据词源学,trie 的发明者 Edward Fredkin 把它读作/ˈtriː/ “tree”。但是,其他作者把它读作/ˈtraɪ/ “try”。trie 中的键通常是字符串,但也可以是其它的结构。trie 的算法可以很容易地修改为处理其它结构的有序序列,比如一串数字或者形状的排列。比如,bitwise trie 中的键是一串位元,可以用于表示整数或者内存地址。trie 树常用于搜索提示。如当输入一个网址,可以自动搜索出可能的选择。当没有完全匹配的搜索结果,可以返回前缀最相似的可能。
前缀树(Trie,也称为字典树或前缀字典树)是一种用于高效存储和检索一组字符串的树形数据结构。前缀树的主要特点是利用共同的前缀来压缩存储相似的字符串,从而节省内存空间,并提高字符串检索的效率。
在前缀树中,每个节点代表一个字符,根节点表示空字符。从根节点到每个节点的路径表示一个字符串。每个节点可能有多个子节点,每个子节点对应于一个可能的字符。如果一个字符串是另一个字符串的前缀,则这两个字符串在前缀树中会共享一部分路径。
前缀树的应用场景很广泛,主要用于字符串的搜索、匹配和自动补全。例如,前缀树常用于实现搜索引擎的搜索功能、单词的拼写检查、自动补全、IP路由表的查找等。由于前缀树能够快速地找到以给定前缀开头的所有字符串,因此在处理大量字符串的情况下,它可以大大提高检索的效率。
以下是一个示例前缀树:
root
/ \
c b
/ \ \
a o y
/ / \ \
r w d e
/ / / \ \
t i r y n
/ / / / \ \
s t n i e t
/ / \ \ /
h e t r a
前缀树的实现
重点在于节点数据结构,重要的插入和查找方法,以及递归和非递归两种形式。
节点数据结构定义
Node节点中使用map较为高效,用于映射到下一个节点:
public class Trie {
private class Node{
public boolean isWord; // 是否是某个单词的结束
public TreeMap<Character, Node> next; //到下一个节点的映射
public Node(boolean isWord){
this.isWord = isWord;
//初始化字典树
next = new TreeMap<>();
}
public Node(){
this(false);
}
}
//根节点
private Node root;
//Trie单词个数
private int size;
public Trie(){
root = new Node();
size = 0;
}
// 获得Trie中存储的单词数量
public int getSize(){
return size;
}
}
插入方法
●非递归方式
向Trie中添加一个新的单词word: 将单词拆分成一个个字符c,然后从根节点开始往下添加
public void add(String word){
Node cur = root;
//循环判断新的cur节点是否包含下一个字符到下一个节点的映射
for(int i = 0 ; i < word.length() ; i ++){
//将c当成一个节点插入Trie中
char c = word.charAt(i);
//判断cur.next是不是已经指向我们要找的c字符相应的节点
if(cur.next.get(c) == null){
//新建节点
cur.next.put(c, new Node());
}
//否则,就直接走到该节点位置即可
cur = cur.next.get(c);
}
//判断该单词并不表示任何一个单词的结尾
if(!cur.isWord){
//确定cur是新的单词
cur.isWord = true;
size ++;
}
●递归方式
/**
* 向Trie中添加一个新的单词word(递归写法接口)
*
* @param word
*/
public void recursionAdd(String word) {
Node cur = root;
add(root, word, 0);
}
/**
* 递归写法调用方法实现递归添加
*
* @param node 传入要进行添加的节点
* @param word 传入要进行添加的单词
*/
public void add(Node node, String word, int index) {
// 确定终止条件,这个终止条件在没加index这个参数时,很难确定
// 此时一个单词已经遍历完成了,如果这个结束节点没有标记为单词,就标记为单词
if (!node.isWord && index == word.length()) {
node.isWord = true;
size++;
}
if (word.length() > index) {
char addLetter = word.charAt(index);
// 判断trie的下个节点组中是否有查询的字符,如果没有,就添加
if (node.next.get(addLetter) == null) {
node.next.put(addLetter, new Node());
}
// 基于已经存在的字符进行下个字符的递归查询
add(node.next.get(addLetter), word, index + 1);
}
}
查询单词方法
●非递归方式
/**
* 查询单词word是否在Trie中(非递归写法)
*
* @param word
* @return
*/
public boolean contains(String word) {
Node cur = root;
for (int i = 0; i < word.length(); i++) {
char c = word.charAt(i);
if (cur.next.get(c) == null) {
return false;
} else {
cur = cur.next.get(c);
}
}
return cur.isWord;
}
●递归方式
/**
* 查询单词word中是否在Trie中接口(递归写法)
*
* @param word
* @return
*/
public boolean recursionContains(String word) {
Node cur = root;
return contains(root, word, 0);
}
/**
* 查询word中是否在Trie中递归写法
*
* @param node
* @param word
* @param index
* @return
*/
private boolean contains(Node node, String word, int index) {
if (index == word.length()) {
return node.isWord;
}
char c = word.charAt(index);
if (node.next.get(c) == null) {
return false;
} else {
return contains(node.next.get(c), word, index + 1);
}
}
查询前缀方法
●非递归方式
/**
* 查询是否在Trie中有单词一prefix为前缀
*
* @param prefix
* @return
*/
public boolean isPrefix(String prefix) {
Node cur = root;
for (int i = 0; i < prefix.length(); i++) {
char c = prefix.charAt(i);
if (cur.next.get(c) == null) {
return false;
}
cur = cur.next.get(c);
}
return true;
}
●递归方式
/**
* 查询是否在Trie中有单词一prefix为前缀(递归调用)
*
* @param prefix
* @return
*/
public boolean recursionIsPrefix(String prefix) {
Node node = root;
return recursionIsPrefix(root, prefix, 0);
}
/**
* 查询是否在Trie中有单词一prefix为前缀(递归实现)
*
* @return
*/
public boolean recursionIsPrefix(Node root, String prefix, int index) {
if (prefix.length() == index) {
return true;
}
char c = prefix.charAt(index);
if (root.next.get(c) == null) {
return false;
} else {
return recursionIsPrefix(root.next.get(c), prefix, ++index);
}
}
前缀树的复杂度
前缀树(Trie)的复杂度如下:
-
插入操作的复杂度:O(m),其中 m 是要插入的字符串的长度。在前缀树中插入一个字符串的时间复杂度取决于字符串的长度。
-
查找操作的复杂度:O(m),其中 m 是要查找的字符串的长度。在前缀树中查找一个字符串的时间复杂度也取决于字符串的长度。
-
删除操作的复杂度:O(m),其中 m 是要删除的字符串的长度。在前缀树中删除一个字符串的时间复杂度也取决于字符串的长度。
-
空间复杂度:O(N * L),其中 N 是所有插入的字符串的总长度,L 是字符串平均长度。由于前缀树存储了所有插入的字符串,空间复杂度为插入字符串的总长度。
需要注意的是,前缀树对于存储大量字符串时可能会占用较大的内存空间。因为它需要为每个字符都创建一个节点,并且可能会导致大量的节点重复。在某些情况下,为了减少内存占用,可以考虑使用压缩的字典树(Compressed Trie)等变种数据结构。压缩的字典树可以将具有相同前缀的节点合并,从而减少了存储空间的使用,但可能会稍微牺牲一些检索效率。
前缀树有哪些应用
前缀树(Trie)由于其高效的字符串存储和检索特性,在许多应用中都得到了广泛的应用。以下是一些前缀树的常见应用:
-
字符串搜索和匹配:前缀树可以快速地搜索和匹配字符串。它常被用于实现搜索引擎的搜索功能,字符串的模式匹配,以及文本编辑器中的查找和替换操作。
-
单词的自动补全:在输入框中,前缀树可以用来实现单词的自动补全功能。当用户输入一个前缀时,前缀树可以快速找到所有以该前缀开头的单词,然后显示给用户选择。
-
单词的拼写检查:前缀树可以用于拼写检查,它可以快速判断一个字符串是否是有效的单词。
-
IP 路由表查找:前缀树被广泛用于路由表查找中,用于快速确定一个IP地址所对应的路由。
-
统计和排序:前缀树可以用于统计和排序字符串。例如,可以用前缀树来找出最常用的前缀,或者找出所有以某个前缀开头的字符串。
-
字符串压缩:前缀树可以用于字符串的压缩,特别是当有许多重复的前缀时,前缀树可以将这些重复的前缀合并在一起,从而减少存储空间。
这只是前缀树应用的一小部分例子,实际上它在很多领域都有应用,特别是在字符串处理和文本搜索方面。由于前缀树的高效性能和灵活性,它被广泛用于处理和存储大量的字符串数据。
前缀树的压缩:基数树
对于前缀树(Trie)来说,压缩是一种优化技术,旨在减少前缀树的存储空间,同时保持其高效的字符串检索功能。基数树(Radix Tree)是一种常见的前缀树压缩技术。
基数树通过合并具有相同前缀的节点来减少存储空间。它会将只有一个子节点的节点与其子节点合并成一个更大的节点。这样做的原因是在前缀树中,存在许多具有相同前缀的节点,而这些节点的子节点可能只有一个。通过合并这些节点,可以节省存储空间,同时保持字符串的前缀信息。
基数树在处理大量具有相同前缀的字符串时,可以显著减少前缀树的节点数量,从而节省内存空间。然而,由于合并操作可能会导致某些路径的唯一性丢失,因此在某些情况下,可能会稍微降低字符串的检索效率。因此,基数树是一种在存储空间和检索效率之间进行权衡的优化方案。
需要根据具体的使用情况来选择是否使用基数树或其他前缀树压缩技术。在某些应用场景中,保持前缀树的原始结构可能更有利于字符串的检索效率,而在其他情况下,使用基数树等压缩技术可以带来更好的存储效率。
双数组Trie树(DoubleArrayTrie)
双数组Trie树(Double-Array Trie,简称DAT或DART)是一种高效的字符串存储和检索数据结构,是对标准Trie树的一种优化。它通过使用两个数组来代替Trie树的节点指针和字符映射表,从而减少了存储空间的消耗,并提高了字符串检索的效率。
双数组Trie树的主要特点是将Trie树的节点信息分别存储在base数组和check数组中。其中,base数组存储节点的位置信息,check数组存储字符的映射关系。通过这种方式,双数组Trie树能够在不损失字符串检索效率的情况下,显著减少存储空间的使用。
双数组Trie树的构建过程包括两个主要步骤:分配base和check数组,然后根据输入的字符串构建双数组Trie树。在构建过程中,需要对字符串进行排序,以保证字符串在双数组Trie树中的位置是连续的。构建完成后,双数组Trie树可以高效地进行字符串的检索、插入和删除操作。
双数组Trie树的优点包括:
-
节省内存:由于使用了两个数组代替节点指针和字符映射表,双数组Trie树能够大幅度减少存储空间的占用。
-
高效检索:双数组Trie树的检索效率与标准Trie树相当,甚至更快。它通过数组的索引操作,实现了快速的字符串匹配。
-
构建效率高:相对于其他字符串存储结构,双数组Trie树的构建过程相对简单,并且具有较高的构建效率。
双数组Trie树在许多字符串处理和文本搜索领域得到广泛应用,特别适用于需要高效存储和检索大量字符串的场景,例如自然语言处理、字典树构建、字符串匹配等。
参考文章
- https://blog.csdn.net/v_july_v/article/details/6897097
- https://www.cnblogs.com/bonelee/p/8830825.html
- https://blog.csdn.net/forever_dreams/article/details/81009580
- https://www.jianshu.com/p/b9b8bf82fcd5
- https://bestqiang.blog.csdn.net/article/details/89103524
- https://java-sword.blog.csdn.net/article/details/89373156
LeetCode–208. 实现 Trie (前缀树)
208. 实现 Trie (前缀树)
https://leetcode.cn/problems/implement-trie-prefix-tree/description/
package 西湖算法题解___中等题;
public class __208实现Trie前缀树 {
class Trie {
private Trie[] children;
private boolean isEnd;
public Trie() {
children = new Trie[26];
isEnd = false;
}
public void insert(String word) {
Trie node = this;
for (int i=0;i<word.length();i++){
char ch = word.charAt(i);
int index = ch -'a';
if (node.children[index] == null){
node.children[index] = new Trie();
}
node = node.children[index];
}
node.isEnd = true; //标识已经结束
}
public boolean search(String word) {
Trie node = searchPrefix(word); //检查当前children[]是否已经存在
return node != null && node.isEnd;
}
private Trie searchPrefix(String word) {
Trie node = this;
for (int i=0;i<word.length();i++){
char ch = word.charAt(i);
int index = ch -'a';
if (node.children[index] == null){
return null;
}
node = node.children[index];
}
return node;
}
public boolean startsWith(String prefix) {
return searchPrefix(prefix) != null;
}
}
}