图算法——求最短路径（Dijkstra算法）

       目录

一、什么是最短路径

二、迪杰斯特拉（Dijkstra）算法

 三、应用Dijkstra算法

（1） Dijkstra算法函数分析

---

        求图的最短路径在实际生活中有许多应用，比如说在你在一个景区的某个景点，参观完后，要怎么走最少的路程到你想参观的下个景点，这就利用到了求图最短路径的算法。求图的最短路径有很多算法，这里介绍一种迪杰斯特拉（Dijkstra）算法来求图的最短路径。

        在介绍算法前，需要掌握一点图的基本知识，比如说什么是路径，什么是路径长度等。如果对这些不了解的话，建议先了解一下。

        这是我写的一篇博客，对图的一些基本知识的简介——图的一些基本知识。

一、什么是最短路径

        在网图和非网图中，最短路径的含义是不同的。由于非网图没有边上的权值，所谓最短路径，其实指的就是两个顶点之间经过的边数最少的路劲（即可以理解为把每一条边的权值看作是1）。

        对于网图来说，最短路径，是指两顶点之间经过的边上的权值之和最少的路径，并且我们称路径上的第一个顶点是源点，最后一个顶点是终点。

        求带权有向图G的最短路径问题一般可分为两类：一是单源最短路径，即求图中某一个顶点到其它顶点的最短路径，可以通过经典的 Dijkstra（迪杰斯特拉）算法求解（即是我要介绍的算法）；二是求每对顶点间的最短路径，可通过Floyd（弗洛伊德）算法来求解。

二、迪杰斯特拉（Dijkstra）算法

        Dijkstra算法算法思路是设置一个集合S记录已求得的最短路径的顶点，初始时把源点V0（图中的某个顶点）放入S，集合S每并入一个新顶点 V，都要修改源点V0到集合 V-S 中顶点当前的最短路径长度值（这里可能大家会很懵，但等会我会用一个例子来解说）。

        在构造过程中需要两个辅助数组：

• dist[ ] ：记录从源点V0到其他各顶点当前的最短路径长度，它的初态为：若从 V0 到 V 有直接路径（即V0 和 V 邻接），则dist[ i ]为这两个顶点边上的权值；否则置 dist[ i ] 为 ∞。
• path[ ]：path[ i ]表示从源点到顶点 i 之间的最短路径的前驱结点。在算法结束时，可以根据其值追溯到源点 V0 到 V 的最短路径。

        假设从顶点 V0 = 0出发，邻接矩阵Edge表示带权无向图，Edge[i][j]表示无向边 (i, j)的权值，若不存在无向边(i, j)，则Edge[i][]为 ∞。

        Dijkstra算法步骤如下：

1）初始化：集合S初始化为{0}，dist[ ] 的初始值dist[i] = Edge[0][i]，path[ ]的初始值path[i] = -1，i = 1,2,...,n-1。

2）从顶点集合 V - S中选出V，满足dist[j] = Min{dist[i] | V  V - S}，V就是当前求的一条从 V0 出发的最短路径的终点，令S = S{j}。

3）修改从V0出发到集合 V - S上任一顶点 V 可达的最短路径长度：若

      dist[j] + Edge[j][k] < dist[k]，则更新 dist[k] = dist[j] + Edge[j][k]，并修改path[j] = k（即修改顶点V的最短路径的前驱结点 ）  。

4）重复 2）~  3）操作共 n-1 次，直到所有的顶点都包含在 S 中。

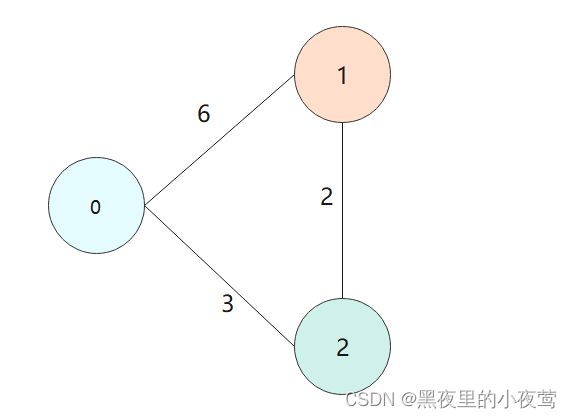
解释下步骤3），每当一个顶点加入S后，可能需要修改源点V0 到集合 V-S中的可达顶点当前的最短路径长度。下面举一个例子。如下图所示，源点为V0，初始时S = {V0}，dist[1] = 6, dist[2] = 3,当V并入集合S后，dist[1] 需要更新为 5（其比6小，即说明两点之间不是直线最短，要根据两点之间路径的权值之和来看）。

下面来讲解利用Dijkstra算法来求下图中的顶点 0 出发至其余顶点的最短路径的过程。

初始化：集合S初始化为{V}，V可达V和V，其余顶点不可达，因此dist[]数组和path[]数组的设置如下：

第一轮：选出最小dist[2]，将顶点 V 并入集合S，此时已找到 V 到 V 的最短路径，S = {V，V}。当 V 加入到S后，从V到集合V-S中可到达顶点的最短路径长度可能会产生变化。因此需要更新dist[]数组。V可达V，因V -> V -> V的距离 5 比 dist[1] = 6小，更新dist[1] = 5，并修改 path[1] = 2（即V的最短路径的前驱为V）；V 可达 V，V -> V - > V的距离 8 比 dist[3] = ∞ 小，更新dist[3] = 8，path[3] = 2；V可达V，V -> V -> V 的距离 10 小于 dist[5] = ∞，更新dist[5] = 10，path[5] = 2。V再无到达其余的顶点的路径，结束这一轮，此时dist[]数组和path[]数组如下：

 第二轮：选出最小值dist[1]，将顶点 V 并入集合S，此时已找到 V 到 V 的最短路径，S = {V,V，V}。然后更新dist[]数组和path[]数组，V可达V，V -> V -> V -> V 的距离 6 小于 dist [3] = 8 ，更新 dist[3] = 6，path[3] = 1；V 可达 V，但V已经在集合S中，故不进行操作；V 可达 V， V -> V -> V -> V的距离 9 小于 dist[4] = ∞，更新dist[4] = 9，path[4] = 1。V 已无到达其余顶点的路径，结束此轮，此时dist[]数组和path[]数组如下：

第三轮： 选出最小值 dist[3]，将顶点 V 并入集合 S，此时已找到 V 到 V 的最短路径，S = { V,V，V，V}。接着更新dist[]数组和path[]数组，V 可到达 V， V -> V -> V -> V -> V 的距离为 9 等于 dist[4] = 9，我们不做更新；V 可到达 V，  V -> V -> V -> V -> V 的距离为 12 大于 dist[5] = 10，不做更新。 V 再无达到其余顶点的路径，结束此轮，此时dist[]数组和path[]数组如下：

第四轮：选出最小值 dist[4]，将顶点 V 并入集合 S，此时已找到 V 到 V的最短路径，S = { V,V，V，V，V}。继续更新dist[]数组和path[]数组，V可到 V， V -> V -> V -> V -> V的距离 11 小于 dist[5] = 10，故不进行更新操作；V 可到 V， V -> V -> V -> V -> V的距离 11 小于 dist[6] = ∞，更新 dist[6] = 11，path[6] = 4。V 再无达到其余顶点的路径，结束此轮，此时dist[]数组和path[]数组如下：

第五轮： 选出最小值 dist[5]，将顶点 V 并入集合S，此时已找到 V 到 V的最短路径，S =  { V,V，V，V，V，V}。然后ist[]数组和path[]数组，V 可到 V， V -> V -> V -> V 的最短路径 13 大于 dist[6]，故不进行更新操作。V 再无达到其余顶点的路径，结束此轮，此时dist[]数组和path[]数组如下： 

 第六轮：选出最小值 dist[6]，将顶点 V 并入集合，此时全部顶点都已包含在S中，结束算法。

 整个算法每一轮的结果如下： 

总结：Dijkstra算法就是最开始选离源点V最近的点，然后选好点后，再从选好点的看其邻接点的距离dist[]是否减小，减小就修改dist[]和path[]；否则就不进行修改操作。Dijkstra算法基于贪心策略，用邻接矩阵表示图时，来使用Dijkstra算法，其时间复杂度为O(n*n)。当边上带有负权值时，Dijkstra算法并不适用。

使用dist[]数组和path[]数组，求最短路径，这里介绍一个例子，其它顶点依次类推。

V到V的最短路径，先利用dist[6] = 11 得出 V到V的距离，然后利用path[]得出路径。path[6] = 4，顶点V的前驱顶点是 V，再由 path[4] = 1,表示 V 的前驱是 V , path[1] = 2，表示 V 的前驱是 V，path[2] = -1，结束。最后可以得到 V 到 V 的最短路径为 V <- V <- V <- V <- V，即 V -> V -> V -> V -> V 。

 三、应用Dijkstra算法

        理解上面的Dijkstra算法求最短路径的过程，那么下面的应用Dijkstra算法的程序就很容易理解。此程序分三大块，在程序末尾我会来粗略介绍下。

使用此程序需输入以下内容创建图G：

第一步：7 12

第二步：0123456

第三步：依次输入下面的内容，输入完一行就按下换行键

0 1 6

0 2 3

1 2 2

1 3 1

1 4 4

2 3 5

2 5 7

3 4 3

3 5 6

4 5 2

4 6 2

5 6 3

        上面输入完后，即可创建下面的图G： 

/*
使用此程序需输入以下内容创建图G：
第一步：7 12
第二步：0123456
第三步：依次输入下面的内容，输入完一行就按下换行键
0 1 6
0 2 3
1 2 2
1 3 1
1 4 4
2 3 5
2 5 7
3 4 3
3 5 6
4 5 2
4 6 2
5 6 3
*/
#include 
#include 
#include 

#define MaxVerterNum 100		// 顶点数目的最大值
#define INFINITY 65535			// 用65535代表 ∞

typedef char VertexType;		// 顶点的数据类型
typedef int EdgeType;			// 带权图中边上权值的数据类型

/* 邻接矩阵的存储结构 */
typedef struct
{
	VertexType Vexs[MaxVerterNum];					// 顶点表
	EdgeType Edge[MaxVerterNum][MaxVerterNum];		// 邻接矩阵
	int vexNum, arcNum;								// 图当前顶点数和弧数
}MGraph;

/*清除缓冲区的换行符*/
void Clean(void)
{
	while (getchar() != '\n')
		continue;
}

/* 建立无向网图的邻接矩阵表示 */
void CreateMGraph(MGraph* G);

/* 迪杰斯特拉（Dijkstra) 算法*/
typedef int Patharc[MaxVerterNum];			// 用于存储最短路径下标的数组，从源点Vi到顶点Vj之间的最短路径的前驱
typedef int ShortPathTable[MaxVerterNum];	// 用于存储到各点最短路径的权值和
void ShortestPath_Dijkstra(MGraph G, int v0, Patharc path, ShortPathTable D);

/* 输出最短路径 */
/* Dijkstra算法的结果输出 */
void Show_ShortestPath_Dijkstra(Patharc path, ShortPathTable dist, MGraph G, int v0);

int main(void)
{
	MGraph G;
	Patharc path;
	ShortPathTable dist;
	CreateMGraph(&G);
	for (int i = 0; i < G.vexNum; i++) // 输出各点到各点的最短路径序列，不再局限于一个顶点
	{
		ShortestPath_Dijkstra(G, i, path, dist);
		Show_ShortestPath_Dijkstra(path, dist, G, i);
	}
	return 0;
}

/* 建立无向网图的邻接矩阵表示 */
void CreateMGraph(MGraph* G)
{
	int i, j, k, w;
	printf("请输入顶点数和边数：");
	scanf("%d %d", &G->vexNum, &G->arcNum);			// 获取无向图顶点数和边数
	printf("请输入全部顶点信息：\n");
	Clean();									    // 将换行符去除
	for (i = 0; i < G->vexNum; i++)					// 读取顶点信息，建立顶点表
		scanf("%c", &G->Vexs[i]);
	for (i = 0; i < G->vexNum; i++)
		for (j = 0; j < G->vexNum; j++)
			G->Edge[i][j] = INFINITY;				// 邻接矩阵初始化
	for (k = 0; k < G->arcNum; k++)					// 读入arcNum条边，建立邻接矩阵
	{
		printf("请输入边（Vi, Vj)上的下标i，下标j和权w：\n");
		scanf("%d %d %d", &i, &j, &w);				// 获取边和权
		G->Edge[i][j] = w;							// 无向图矩阵对称
		G->Edge[j][i] = G->Edge[i][j];
	}
	return;
}

/* 迪杰斯特拉（Dijkstra) 算法*/
void ShortestPath_Dijkstra(MGraph G, int v0, Patharc path, ShortPathTable dist)
{
	int v, w, k, min;
	int final[MaxVerterNum];				/* final[w] = 1表示求得顶点 v0 至 vw的最短路                    径，即已访问过顶点vw*/
	for (v = 0; v < G.vexNum; v++)
	{
		final[v] = 0;						// 全部顶点初始化为未知最短路径状态
		dist[v] = G.Edge[v0][v];			// 将与v0点有连线的顶点加上权值
		path[v] = -1;						// 初始化路劲数组p为-1
	}
	dist[v0] = 0;							// v0至v0路径为0
	final[v0] = 1;							// v0至v0不需要路径
	/* 开始主循环，每次求得v0到某个顶点v的最短路径*/
	for (v = 1; v < G.vexNum; v++)
	{
		min = INFINITY;						// 当前所知离v0顶点的最近距离
		for (w = 0; w < G.vexNum; w++)		// 寻找离v0最近的顶点
		{
			if (!final[w] && dist[w] < min)
			{
				k = w;
				min = dist[w];				// w顶点离v0顶点更近
			}
		}
		final[k] = 1;						// 将目前找到的最近的顶点置为1
		for (w = 0; w < G.vexNum; w++)		// 修正当前最短路径及距离
		{
			/* 如果经过v顶点的路径比现在这条路径的长度短的话 */
			if (!final[w] && (min + G.Edge[k][w] < dist[w]))
			{
				/* 找到了更短的路径，修改D[w]和P[w] */
				dist[w] = min + G.Edge[k][w];	// 修改当前路径长度
				path[w] = k;
			}
		}
	}
}

/* 输出最短路径 */
/* Dijkstra算法的结果输出 */
void Show_ShortestPath_Dijkstra(Patharc path, ShortPathTable dist, MGraph G, int v)
{
	int w, k;
	printf("V%d到各点的最短路径如下：\n", v);
	for (w = 0; w < G.vexNum; w++)
	{
		if (w != v)
		{
			printf("V%d-V%d weight: %d", v, w, dist[w]);
			k = path[w];
			printf(" path: V%d", w);
			while (k != -1)  // 当 k = -1 ，结束循环并输出源点
			{
				printf(" <- V%d", k);
				k = path[k];
			}
			printf(" <- V%d\n", v);
		}
	}
	printf("\n");
}

（1） Dijkstra算法函数分析

/* 迪杰斯特拉（Dijkstra) 算法*/
void ShortestPath_Dijkstra(MGraph G, int v0, Patharc path, ShortPathTable dist)
{
	int v, w, k, min;
	int final[MaxVerterNum];				// final[w] = 1表示求得顶点 v0 至 vw的最短路径，即已访问过顶点vw
	for (v = 0; v < G.vexNum; v++)
	{
		final[v] = 0;						// 全部顶点初始化为未知最短路径状态
		dist[v] = G.Edge[v0][v];			// 将与v0点有连线的顶点加上权值
		path[v] = -1;						// 初始化路劲数组p为-1
	}
	dist[v0] = 0;							// v0至v0路径为0
	final[v0] = 1;							// v0至v0不需要路径
	/* 开始主循环，每次求得v0到某个顶点v的最短路径*/
	for (v = 1; v < G.vexNum; v++)
	{
		min = INFINITY;						// 当前所知离v0顶点的最近距离
		for (w = 0; w < G.vexNum; w++)		// 寻找离v0最近的顶点
		{
			if (!final[w] && dist[w] < min)
			{
				k = w;
				min = dist[w];				// w顶点离v0顶点更近
			}
		}
		final[k] = 1;						// 将目前找到的最近的顶点置为1
		for (w = 0; w < G.vexNum; w++)		// 修正当前最短路径及距离
		{
			/* 如果经过v顶点的路径比现在这条路径的长度短的话 */
			if (!final[w] && (min + G.Edge[k][w] < dist[w]))
			{
				/* 找到了更短的路径，修改D[w]和P[w] */
				dist[w] = min + G.Edge[k][w];	// 修改当前路径长度
				path[w] = k;
			}
		}
	}
}

         上面数组final[]保存已有路径的结点，有最短路径的结点的值为 1，无最短路径的结点的值为 0，path[]数组记录结点 V 的前驱结点，dist[]数组，记录结点 V 的前驱结点。

        首先进行初始化，final[]数组的元素的值均为 0，path[]数组的值均为 -1,当path[i]=-1时，说明此结点的前驱结点即是源点V，dist[]的元素值初始化为源点V到邻接点的距离。

        接着进入for循环，for循环内的第一个for循环用于找到 dist[] 数组的最小值。

        for循环内的第二个for循环用于进行修正。

        以上便是Dijkstra算法函数的基本内容。三大块——初始化，找dist[]最小元素、修正路径。

---

人生是一场无休、无歇、无情的战斗，凡是要做个够得上称为人的人，都得时时向无形的敌人作战。                                                                                                           ——罗曼·罗兰

以此句献给看这篇博客的每一个人。