「二叉树与递归的一些框架思维」

0 二叉树

二叉树的递归解法，总的来说就是两类思路，第一类是遍历一遍二叉树得出答案，第二类是通过分解问题计算出答案，而遍历二叉树得出答案的思维对应着回溯算法；分解二叉树对应着动态规划算法。二叉树又是核心的数据结构，接下来的树的衍生以及图的应用都是基于二叉树，所以二叉树非常重要。下方将总结二叉树框架思维，用题目来举例。

二叉树的前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点，绝非仅仅只是一个链表这么简单，前序位置就是刚进入一个节点（元素）的时候（自顶向下）（前序位置，你能获得的参数，只有父类节点给的参数），后序位置就是即将离开一个节点（元素）的时候（自顶向上）（后序位置，你除了父类节点的参数，还有遍历到下面后，子类节点给你的参数，所以说啊，如果面试题当中，和子树题有关的，那么大概率是要在后序的位置处写上合理的代码），中序位置就是遍历完左子树，即将遍历右子树的时候。 这就是为什么递归其实上是系统帮我们维护了一个栈的原因，二叉树的前序遍历等这些遍历其实也是依靠了栈的技术，前序就是入栈，后序就是出栈，这两个方向是相反的。

二叉树的题目，就是在这三个时间点，插入正确的代码，多叉树为什么没有中序位置？因为多叉树的子树太多了，不好确认中序节点位置。

1 思路

综上，遇到一道二叉树的题目时，按照东哥的通用思考过程来说就是：

1. 是否可以通过遍历一遍二叉树得到答案？如果可以，用一个 traverse 函数配合外部变量来实现。

2. 是否可以定义一个递归函数，通过子问题（子树）的答案推导出原问题的答案？如果可以，写出这个递归函数的定义，并充分利用这个函数的返回值。

3. 无论使用哪一种思维模式，你都要明白二叉树的每一个节点需要做什么，需要在什么时候（前中后序）做。

2 刷题

2.1 二叉树的最大深度

题解

求解二叉树的深度，可以用二叉树的遍历来完成，使用depth来记录访问的深度，使用res来记录真正的深度，depth在前序位置加一（入栈），在后序位置减一（出栈），然后再更新res即可。

或者方法2，二叉树的最大深度其实可以通过子树来推导出来（看左子树的最大深度和右子树的最大深度哪个更大，返回最大值+1（根节点）即可），这就是分解问题的思想。

一个特别重要的点就是，分解问题一定要把函数定义给搞明白。

例如二叉树的前序遍历，可以分解成：根节点+左子树的前序遍历+右子树的前序遍历，代码如下：

//函数定义：给定一颗二叉树的根节点，返回这棵树的前序遍历节点
list<int> preorderTraverse(TreeNode *root)
{
	list<int> res;
	if (root == nullptr) return res;
	//前序遍历，先加入根节点
	res.add(root->val);
	//前序遍历左子树，利用函数定义，给了你左子树的根节点你就能给出左子树的前序遍历
	res.addAll(preorderTraverse(root->left)); 
	//前序遍历右子树，利用函数定义，给了你右子树的根节点你就能给出右子树的前序遍历
	res.addAll(preorderTraverse(root->right)); 
	return res;
}

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    int res = 0, depth = 0;
    //res记录最大深度，depth记录遍历到的最大深度
public:
    int maxDepth(TreeNode* root) {
        traverse(root);
        return res;
    }

    void traverse(TreeNode* root)
    {
        //判断非空
        if (root == nullptr) return;
        //前序位置
        ++depth;
        if (!root->left && !root->right)
        {
            res = max(res, depth);//更新一下res
        }
        traverse(root->left);
        traverse(root->right);
        //后序位置
        --depth;
    }
};

分解问题思想：把整棵树的问题分解为左右子树的问题

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    //函数的作用是，输入一个节点，就能知道这个树的最大深度
    int maxDepth(TreeNode* root) {
        if (root == nullptr) return 0;

        int leftmax = maxDepth(root->left);//看左子树的最大深度
        int rightmax = maxDepth(root->right);//看右子树的最大深度
        
        int res = max(leftmax, rightmax);//更新

        return res + 1;//返回，加上2根节点即可
    }
};

结果

2.2 二叉树的直径

题解

首先给出函数定义，给你一个节点，返回这个节点的最大直径，那么好，算法本质上是穷举，我们通过我们给定的这个函数，计算出所有节点的最大直径，然后返回一个最大的即可。那么，一个节点的最大直径该如何去算呢，把一个节点的左子树右子树的最大深度加起来即可。

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    int maxDiameter;
public:
    //算法定义：给你一个节点，返回最大直径长度
    int diameterOfBinaryTree(TreeNode* root) {
        traverse(root);
        return maxDiameter;
    }

    //遍历一颗二叉树
    void traverse(TreeNode* root)
    {
        if (root == nullptr) return;
        //对每个节点计算最大半径
        int leftmax = maxDepth(root->left);
        int rightmax = maxDepth(root->right);
        int myDiameter = leftmax + rightmax;//节点的直径

        maxDiameter = max(maxDiameter, myDiameter);//更新

        traverse(root->left);
        traverse(root->right);

    }

    //计算最大深度
    int maxDepth(TreeNode *root)
    {
        int depth = 0, res = 0;
        if (root == nullptr) return 0;

        //前序位置
        depth++;
        if (!root->left && !root->right)
        {
            res = max(res, depth);
        }
        int leftmax = maxDepth(root->left);
        int rightmax = maxDepth(root->right);
        return max(leftmax, rightmax) + 1;
    }
};

算最大深度的时候，也是在递归，上面遍历的时候，还是在递归，相当于递归中套递归了，效率不行。考虑一下，是因为在遍历二叉树的时候，在前序位置，在算子树的信息，但是前序位置，你只有父类节点的信息，没有子树的信息，那么可不可以把前序中运用到子树信息的内容搬运到后序提高效率呢？优化：把计算直径的这个过程放到后序的位置（maxDepth这个函数的后序位置），如下代码。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
private:
    // 记录最大直径的长度
    int maxDiameter = 0;
public:
    int diameterOfBinaryTree(TreeNode* root) {
        maxDepth(root);
        return maxDiameter;
    }

    int maxDepth(TreeNode* root) {
    if (root == nullptr) {
        return 0;
    }
    int leftMax = maxDepth(root->left);
    int rightMax = maxDepth(root->right);
    // 后序位置，顺便计算最大直径
    int myDiameter = leftMax + rightMax;
    maxDiameter = max(maxDiameter, myDiameter);

    return 1 + max(leftMax, rightMax);
    }
};

可以看到，遍历了一遍就完成了。

结果

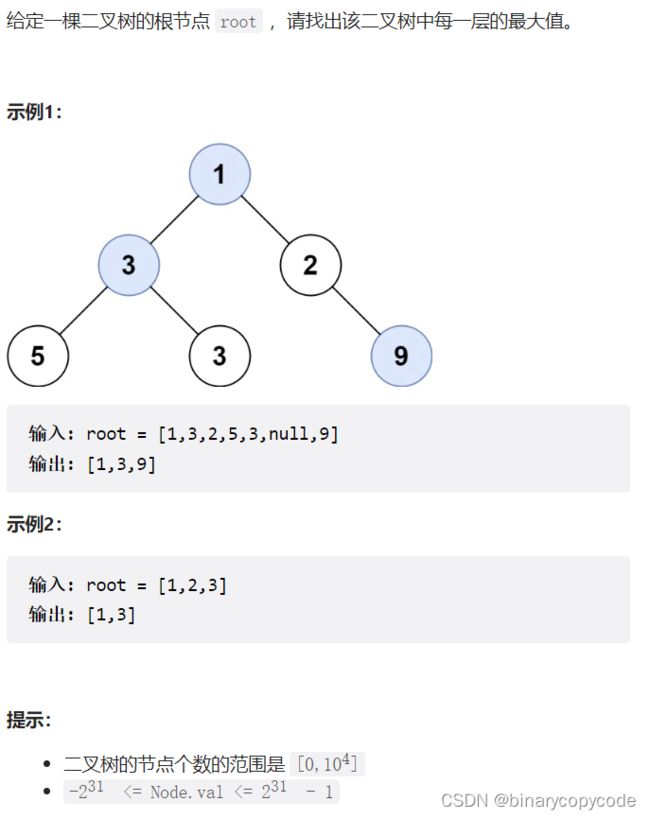
2.3 在每个树行中找最大值

题解

很明显，应该采用树的层序遍历，遍历每一层，找到最大值即可。

// 输入一棵二叉树的根节点，层序遍历这棵二叉树
void levelTraverse(TreeNode* root) {
    if (root == nullptr) return;
    Queue<TreeNode*> q;
    q.push(root);

    // 从上到下遍历二叉树的每一层
    while (!q.empty()) {
        int sz = q.size();
        // 从左到右遍历每一层的每个节点
        for (int i = 0; i < sz; i++) {
            TreeNode* cur = q.pop();
            // 将下一层节点放入队列
            if (cur->left != nullptr) {
                q.push(cur->left);
            }
            if (cur->right != nullptr) {
                q.push(cur->right);
            }
        }
    }
}

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    vector<int> largestValues(TreeNode* root) {
        vector<int> res;
        if (root == nullptr) {
            return {};
        }
        queue<TreeNode*> q;
        q.push(root);
        // while 循环控制从上向下一层层遍历
        while (!q.empty()) {
            int sz = q.size();
            // 记录这一层的最大值
            int levelMax = INT_MIN;
            // for 循环控制每一层从左向右遍历
            for (int i = 0; i < sz; i++) {
                TreeNode* cur = q.front();
                q.pop();
                levelMax = max(levelMax, cur->val);//每弹出一个，就与max进行比较更新
                if (cur->left != nullptr)
                    q.push(cur->left);
                if (cur->right != nullptr)
                    q.push(cur->right);
            }
            res.push_back(levelMax);
        }
        return res;
    }
};

结果

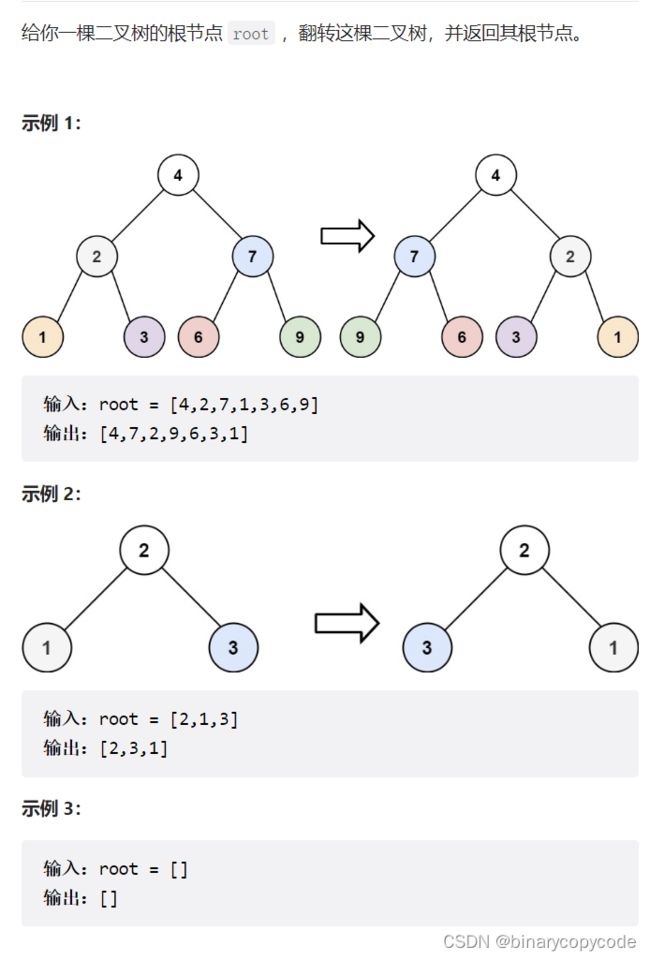
2.4 翻转二叉树

题解

利用分解问题的思想，你看这是一颗树，要翻转这棵树，先翻转他的左子树，再翻转他的右子树，全部翻转完后，交换左右节点即可。

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    //函数定义：给一个根节点，返回翻转后的二叉树
    TreeNode* invertTree(TreeNode* root) {
        if (!root) return root;
        TreeNode* left = invertTree(root->left);//翻转左子树
        TreeNode* right = invertTree(root->right);//翻转右子树

        root->left = right;
        root->right = left;

        return root;
    }
};

结果

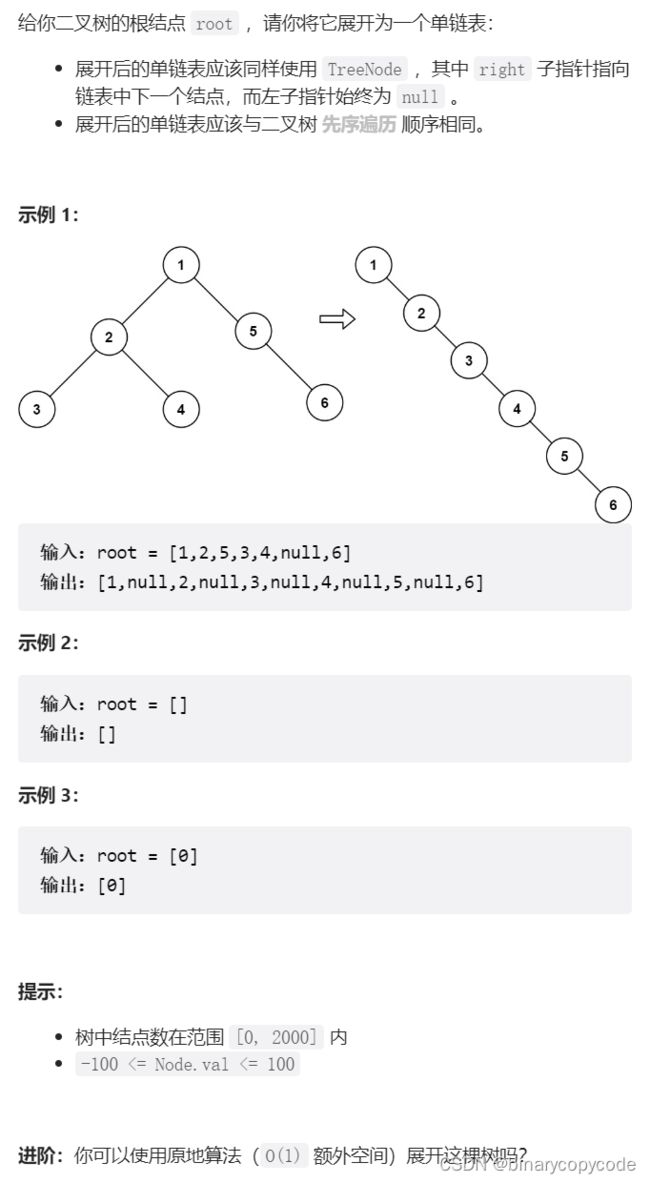
2.5 二叉树展开为链表

题解

对于一个节点 x，可以执行以下流程：

1. 先利用 $flatten(x->left)$ 和 $flatten(x->right)$ 将 $x$ 的左右子树拉平。

2. 将 $x$ 的右子树接到左子树下方，然后将整个左子树作为右子树。

3. 别管$flatten$怎么拉平的，只知道他的作用是这个就行。

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    //采用分解问题的思想
    //给定一下这个函数定义：就是给定一个树的根节点，然后将树展平成链表
    void flatten(TreeNode* root) {
        if (!root) return;
        
        //将左右子树展平
        flatten(root->left);
        flatten(root->right);
        
        //后序位置
        //此时左右子树展平了
        //现在就是要把右子树接到左子树上
        TreeNode* left = root->left;
        TreeNode* right = root->right;

        root->left = nullptr;//先左子树（2,3,4）置为空，没关系，上方保存了
        root->right = left;//再把这个左子树（2,3,4）当成现在的右子树
        //接上
        TreeNode* p = root;
        while (p->right != nullptr) {
            p = p->right;
        }
        p->right = right;//把原先的右子树（5,6）接上刚刚的左子树（2,3,4）之后

    }
};

/*对于一个节点 x，可以执行以下流程：

1、先利用 flatten(x.left) 和 flatten(x.right) 将 x 的左右子树拉平。

2、将 x 的右子树接到左子树下方，然后将整个左子树作为右子树。
*/

结果

2.6 每日一题：数组中两元素的最大乘积

题解

直接排序，然后最后两个就是第一大和第二大的数。

Code

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        sort(nums.begin(), nums.end());
        return (nums[nums.size() - 1] - 1) * (nums[nums.size() - 2] - 1);
    }
};

结果