【GNN+加密流量】NE-GConv: A Lightweight Node Edge Graph Convolutional Network for Intrusion Detection

论文名称

中文题目：NE-GConv:用于入侵检测的轻量级节点边图卷积网络
发表期刊：Computers & Security
发表年份：2023-5
作者：Tanzeela Altaf，Xu Wang, Wei Ni
latex引用：

@article{altaf2023ne,
  title={NE-GConv: A lightweight node edge graph convolutional network for intrusion detection},
  author={Altaf, Tanzeela and Wang, Xu and Ni, Wei and Liu, Ren Ping and Braun, Robin},
  journal={Computers \& Security},
  volume={130},
  pages={103285},
  year={2023},
  publisher={Elsevier}
}

摘要

资源约束设备已成为网络犯罪分子发动网络攻击的首选工具。网络入侵检测系统(NIDS)在网络攻击检测中起着至关重要的作用。最新的图神经网络(GNN)技术通过图结构数据进行学习，从而可以捕捉网络的影响，在网络攻击检测方面取得了广泛的成果。然而，大多数GNN方法都局限于考虑节点特征或边特征。

我们提出的方法克服了这一限制，提出了一个节点边图卷积网络(NEGConv)框架，该框架同时配备了节点和边特征。其中，结合IP地址和端口号形成网络图，分别从报文内容和网络流数据中定义节点和边特征。然后，设计了一个两层模型，该模型通过显式地使用节点和边特征来隐式地进行边分类。因此，该模型对数据包内容和网络流的入侵都很敏感。此外，我们的框架通过在NEGConv之前使用特征选择单元和最小化NE-GConv中的隐藏层数量来解决轻量级设备的限制。实验结果表明，我们的模型在准确率和假阳性率方面优于其他GNN模型，并且计算效率高。

存在的问题

1. 传统模型的检测效果差，并且在计算成本和内存方面需要大量的资源。
2. 现有GNN模型都局限于考虑节点特征或边特征

论文贡献

1. 提出了一种新的图结构来全面地捕捉网络流量关系，其中节点被称为主机，边被称为节点之间的通信。网络数据特征与节点或边具有结构关联。我们将网络数据包内容/应用程序级别的特征分别称为节点特征，将网络流称为边特征。这捕获了网络图结构中主机和流连接的流量特征。
2. 提出了一种对节点和边特征入侵敏感的两层节点边图卷积(NE-GConv)模型。定义了一个新的聚合函数，用于在NE-GConv的消息传递阶段对节点和边特征(负载和流)进行学习、聚合和泛化。
3. 我们开发了一个轻量级IDS框架来满足资源约束设备的部署需求。IDS框架采用递归特征消除(RFE)算法选择NE-GConv的最小输入特征集，并在NE-GConv中实现高效的两层架构。

论文解决上述问题的方法：

1. 提出了一个轻量级的GNN模型
2. 提出的新模型可以同时对节点和边进行学习、聚合和泛化。

论文的任务：

入侵检测，二分类：图的边级别分类问题

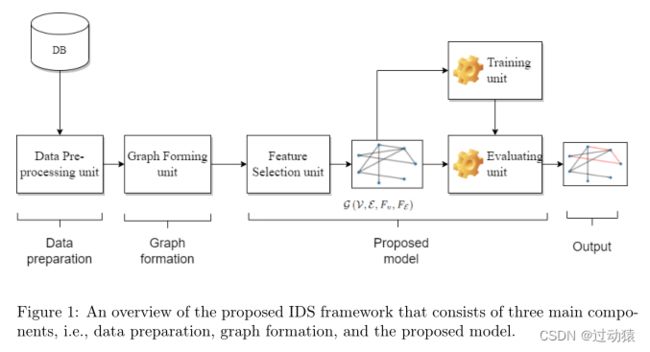
1. IDS框架

• 数据预处理单元：数据清理；标签编码；特征归一化。
• 图构建单元：构图
• 特征选择单元：该单元通过使用RFE技术从原始数据集中过滤出最佳特征来执行特征选择任务
• 训练单元：对模型进行训练
• 评估单元：该单元负责对建议的训练模型进行测试和评估。

2. 图构建

• 节点 $V$：主机，通过配对IP-Port来表示主机，从而构建图形节点
• 节点特征 $F_v$：包括主机特定的观测值，例如负载字段。源节点到目标节点的连接
• 边 $E$：两台发生通信的主机之间就连一条边
• 边的特征 $F_e$：例如流的持续时间、包数和到达时间

由于攻击可能发生在主机和网络级别，因此包含节点和边特征以识别异常情况至关重要。

3. NE-GConv

具体就是使用了两层改进后的GCN，图的边分为恶意和正常两种类型，任务目标是对图的边类型进行分类。

改进后的GCN：

传统的GCN的消息传递函数只考虑聚合的节点特征。为了实现模型中节点特征和边特征的协同效应，必须对标准GConv模型进行修改，使其包含边特征。因此重新构建了一个聚合公式：

$$AGG(F_{v_i},F_{v_j},F_{{\epsilon }_{ij}})=\sum _{v_j\in N_G(v_i)\cup (v_j)}{F}_{{\epsilon }_{ij}}◦F_{v_j}$$
其中◦表示逐元素运算。举例来说就是，假设节点1和2，1和3相邻。那么$F_{{\epsilon }_{11}}$ 维度为 [1, edge_feature]，$F_{v_1}$ 维度为 [1, node_feature]；$F_{{\epsilon }_{12}}$ 维度为 [1, edge_feature]，$F_{v_2}$ 维度为 [1, node_feature]；$F_{{\epsilon }_{13}}$ 维度为 [1, edge_feature]，$F_{v_3}$ 维度为 [1, node_feature]；。将他们进行逐元素运算，即$F_{{\epsilon }_{11}}$◦$F_{v_1}$+$F_{{\epsilon }_{12}}$◦$F_{v_2}$+$F_{{\epsilon }_{13}}$◦$F_{v_3}$（注意：这里只有当edge_feature==node_feature才能完成逐元素相乘。）算出来的结果的维度为[1, edge_feature]

注意：该公式中$v_j$包括自身节点

具体算法流程如下：

总结

1. 论文优缺点

   优点：

   1. 对传统的GCN进行了改进，使其能够聚合节点特征和边特征

   缺点：

   1. 创新点有待考究，节点特征和边特征逐个相乘再相加必须要保证节点特征的维度和边特征维度相同，并且逐个相乘感觉并没有理论依据。
   2. 讨论的不深入，例如：没有讨论图结构的具体类型，不同的图适用于不同的模型；而且也没有对图的规模进行讨论。
   3. 主机特征并没有说的很清楚

感觉这篇文章问题很大：创新点理论根本行不通，图的节点个数和边的个数必须一致，节点特征数量也必须和边的数量一致才能跑通神经网络。