看完这篇,你也可以手撕链表
文章目录
- 一、链表概念及其结构
-
- 1.1 链表和数组的区别
- 1.2 单向链表定义
-
- 链表属性定义
- 节点属性定义
- 二、单链表的基本操作(无虚拟头节点)
-
- 2.1 头插法
- 2.2 遍历链表
-
- head头节点是否可以遍历链表
- 2.3 在index索引处插入新元素val
-
- 核心操作:找待插入位置的前驱节点
- 额外知识点:面向对象的优点
- 2.4 尾插法
- 2.5 查询
-
- 查询第一个值为val的索引
- 判断链表中枢否存在值为val元素
- 查询索引为index的节点val
- 2.6 修改
- 2.7 删除(重点)
-
- 删除核心操作:找前驱
- 删除索引为index的val
- node=null和node.next=null
- 删除第一次出现val的元素(考虑边界)
- 删除链表中所有值为value的节点(面试重点)
-
- 删除所有val节点操作总结
- 删除所有val节点的递归解法
- 删除操作总结
- 三、单链表的增删改查(有虚拟头节点)
-
- 3.1 头插法
- 3.2 在index位置插入元素
- 3.3 删除index位置的元素
- 四、链表面试题
-
- 4.1快慢指针I
-
- 快慢指针II
- 快慢指针III
- 进阶
- 4.2合并链表
-
- 递归
- 分割链表
- 4.3 相交链表
- 4.4 环形链表I
- 4.5 环形链表II(数学分析)
- 4.6 删除重复元素I
-
- 递归求解
- 带虚拟头节点解法
- 4.7 删除重复元素II
- 4.8 删除重复元素III(面试重点)
-
-
- 递归解法
-
- 4.9 反转链表I
-
- 递归解法
- 4.10 反转链表II
- 五、双向链表
-
-
- 6.1头插法
- 6.2尾插法
- 6.3根据索引插入节点(中间位置插入)
- 6.4双向链表删除(分治思想)
-
一、链表概念及其结构
1.1 链表和数组的区别
链表是一种物理存储结构上非连续存储结构,数据元素的逻辑顺序是通过链表中的引用链接次序实现的 。

数组是两个元素在物理结构上紧紧相连

1.2 单向链表定义
链表属性定义

head:头节点
size:当前链表中包含的节点个数

每—列火车由若干个车厢组成,每个车厢就是一个Node对象,由多个Node对象组成的大实体就是链表对象。
/**
* 基于整形的单链表
* */
public class singleLinkList {
//单链表头节点
private Node head;
//当前节点个数=有效数值的个数
private int size;
}
节点属性定义
/**
* 单链表具体的每个节点
*/
class Node {
int val;//每个结点的值
Node next;//当前节点指向下一个节点的地址
}
二、单链表的基本操作(无虚拟头节点)
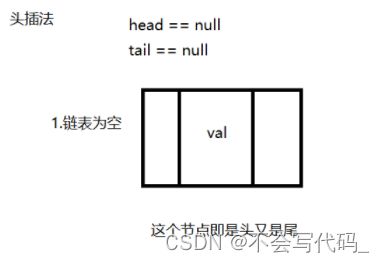
2.1 头插法
具体步骤:
1.创建新节点,并给新节点赋值
2.第一种情况:如果链表中没有头节点,新节点就是头节点,head=newNode
3.第二种情况:链表中存在头节点,需要先newNode.next=head,然后再进行head=newNode,这两个操作的顺序很重要,不可以颠倒

代码如下(示例):
/**
* 向当前链表插入新节点 - 头插法
* @param val
*/
public void addFirst(int val){
Node newNode=new Node(val);
if(head!=null){
newNode.next=head;
}
head=newNode;
size++;
}
无论单链表最后是否为空,新节点都是单链表头插法后新的头节点head=node

2.2 遍历链表
从当前头节点开始,依次取出每个节点值,然后通过next引用走到下一个节点,直到走到链表的末尾(next = null)
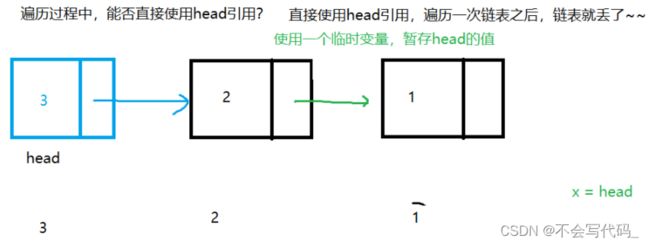
head头节点是否可以遍历链表
不可以。直接使用head引用,遍历一次链表之后,链表就丢了。所以要使用一个临时变量,暂存head的值。只要拿到链表头节点就一定可以遍历整个链表。
代码如下(示例):
/**
* 单链表的打印方法
* @return
*/
public String toString(){
String str="";
Node x=head;
while (x!=null){
str+=x.val;
str+="->";
x=x.next;
}
str+="Null";
return str;
}
2.3 在index索引处插入新元素val
核心操作:找待插入位置的前驱节点
找到前驱节点后,操作1和操作2的顺序如何?能否颠倒?
操作顺序为先2后1,不可以颠倒顺序,如果先1后2,新创建的节点又是自己连接自己。

单链表的插入和删除,最核心的就是在找前驱结点,因为链表只能从前向后操作。但是链表中的头节点很特殊,只有头节点没有前驱节点。
易错点:
1.前驱节点prev要走的步数:找到待插入位置的前驱就是让prev引用从头结点开始先后走index -1步恰好就走到前驱结点(带入具体实例即可求出)
2.index索引指的是,新节点插入后的索引值就是index
/**
* 在单链表的任意索引位置插入新元素val
* @param index
*/
public void add(int index,int val){
//1.判断插入索引index的合法性
//==size就相当于尾插法
if(index<0||index>size){
System.err.println("index is illegal");
}
//2.找前驱节点
//头节点需要特殊处理,头节点不存在前驱节点,直接头插法
if(index==0){
addFirst(val);
}else{
//3.索引位置合法,且不是头节点,找到相应的前驱节点
//前驱节点从头开始遍历
Node prev=head;
//创建待插入新节点
Node newNode=new Node(val);
//index - 1需要通过画图求解
for (int i = 0; i <index-1 ; i++) {
prev=prev.next;
}
//此时prev已经走到待插入index的前驱节点
newNode.next=prev.next;
prev.next=newNode;
size++;
}
}
额外知识点:面向对象的优点
链表和数组的add方法名使用规则完全相同,只需更改类就可以实现链表到数组的转换

2.4 尾插法
//尾插法
public void addLast(int val){
//直接复用在index位置插入元素的办法
addIndex(size,val);
}
2.5 查询
查询第一个值为val的索引
/**
* 查询第一个值为val元素的索引
* @return
*/
public int getByVal(int val){
int index=0;
//遍历链表的方法
for (Node x=head;x!=null;x=x.next){
if(x.val==val){
return index;
}
index++;
}
//for循环之后没有返回相应的index,说明不存在val
//返回一个非法索引下标
return -1;
}
判断链表中枢否存在值为val元素
/**
* 判断链表中是否包含值为val元素
* @param val
* @return
*/
public boolean contains(int val){
int index=getByVal(val);
return index!=-1;
}
不借助方法也可以判断:直接for循环遍历链表,如果node.val==val就return true否则return false
查询索引为index的节点val
/**
* index合法性判断
* @param index
* @return
*/
private boolean rangeCheck(int index) {
if(index<0||index>size){
return false;
}
return true;
}
根据索引index的值,查询index位置元素的val值
/**
* 根据索引index返回相应的val
* @param index
* @return
*/
public int get(int index){
if(rangeCheck(index)){
Node x=head;
for (int i = 0; i < index; i++) {
x=x.next;
}
return x.val;
}
return -1;
}
2.6 修改
/**
* 修改index位置val为newVal,并放回修改前的val值
* @param index
* @param newVal
* @return
*/
public int set(int index,int newVal){
if(rangeCheck(index)){
Node x=head;
for (int i = 0; i < index; i++) {
x=x.next;
}
int oldVal=x.val;
x.val=newVal;
return oldVal;
}
System.err.println("index is illegal!set error");
return -1;
}
2.7 删除(重点)
删除核心操作:找前驱
操作1和2不能颠倒顺序
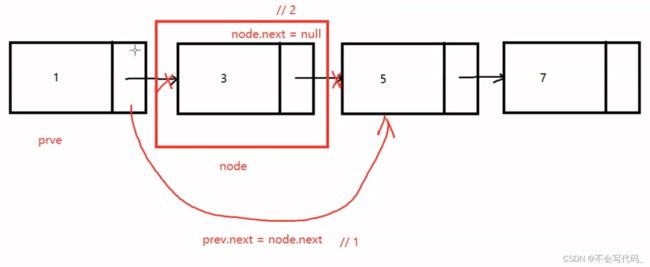
头节点需要特殊处理:头节点没有前驱
一个对象只有没有被任何引用指向,才能被JVM回收

删除索引为index的val
/**
* 删除index位置节点,并返回该节点val
* @param index
* @return
*/
public int remove(int index){
if(rangeCheck(index)){
//特殊处理:头删
if(index==0){
Node x=head;
head=head.next;
x.next=null;
return x.val;
}else{
//删除中间节点
//找前驱
Node prev=head;
for (int i = 0; i < index-1 ; i++) {
prev=prev.next;
}
//此时prev位于待删除节点的前驱
Node node=prev.next;
prev.next=node.next;
node.next=null;
size--;
return node.val;
}
}
System.err.println("index is illegal!remove error");
return -1;
}
node=null和node.next=null
node=null不等于node.next=null

node==null,node中包含的next引用还存在,就是图中的连线

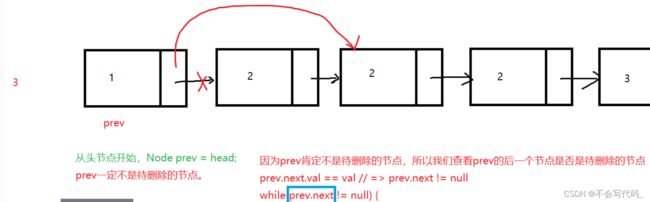
删除第一次出现val的元素(考虑边界)
头节点需要特殊处理:

前驱节点一定不是待删除节点,在保证prev!=null的前提下,还需要保证prev.next!=null,因为我们需要判断的是prev.next.val是否为待删除节点,如果不保证prev.next!=null就可能出现空指针异常的情况!

/**
* 删除链表中第一次出现val的节点
* @param val
*/
public void removeValOnce(int val){
//判空
if(head==null){
System.err.println("head is null!can not removeVal!");
return;
}
//头节点为待删除节点
if(head.val==val){
Node node=head;
head=head.next;
//断内部引用
node.next=null;
//JVM回收整个引用
node=null;
size--;
}else{
//头节点不是待删除节点的情况
Node prev=head;
//前驱节点不是待删除节点
//需要判断prev节点的后继val值,所以要保证prev.next不为null
while (prev.next!=null){
if(prev.next.val==val){
Node node=prev.next;
prev.next=node.next;
node.next=null;
node=null;
return;
}
prev=prev.next;
}
}
}
删除链表中所有值为value的节点(面试重点)
此时不可以使用上面删除第一个出现value元素的方法,因为有可能出现连续的重复的节点,比如在第一个重复元素删除后,prev=prev.next指针向后移动就停留在第二个重复元素节点上,但是if语句判断的是prev.next.val是否为待删除元素,就可能导致少删除一个重复元素。


特殊情况:头节点开始才出现连续的待删除元素
需要保证头节点一定不是待删除元素

使用.操作符要保证实例对象不能为null!!!!

/**
* 删除链表中所有为val的元素
* @param val
*/
public void removeAllVal(int val){
//特殊情况:头节点就出现连续的重复元素val
//可能整个链表都是重复val,一直head=head.next就为空了
//不能使用if语句要使用while是因为不确定头节点出现几个连续重复元素
//保证head不为空
while (head!=null&&head.val==val){
Node node=head;
head=head.next;
node.next=null;
node=null;
size--;
}
//判空:因为可能出现一个链表全是重复元素
if(head==null){
return;
}else {
//保证头节点不是待删除元素且头节点不为空
Node prev=head;
//找到待删除元素节点前驱
while (prev.next!=null){
if(prev.next.val==val) {
Node node = prev.next;
prev.next= node.next;
node.next=null;
node=null;
size--;
}else{
//只有当prev.next.val不等于val才能向前移动
prev=prev.next;
}
}
}
}
删除所有val节点操作总结
1.易错点:特殊情况存在头节点为重复元素val,所以一定使用while循环判断head是否是待删除的节点
2.易错点:特殊情况还包含所有元素为val,所以在所有元素遍历完之后,还要进行一步头节点的判空操作
3.在保证头节点不是待删除元素之后,每次删除重复val后,必须保证prev.next不为空且元素不为重复元素val才可以进行prev=prev.next操作
删除所有val节点的递归解法
相当于把头节点拿出来,剩下的节点交给子方法去处理。最后再判断一下头节点是否等于val,等于的话返回head.next。被子函数处理过的链表一定不会包含val元素了。

public ListNode removeElements(ListNode head, int val) {
if (head == null) {
return null;
}
head.next = removeElements(head.next, val);
//处理头结点
if (head.val == val) {
return head.next;
} else {
return head;
}
}
删除操作总结
1.先处理特殊节点——头节点,保证头节点不为空且头节点不是待删除节点
2.创建前驱节点prev==head,前驱节点一定不是待删除节点,然后遍历链表
3.遍历链表:必须保证prev.next一定不为空,前驱节点不为待删除节点就一定是判断prev.next是否为待删除节点
4.找到待删除节点的前驱,删除三连:
Node node=prev.next
prev.next=node.next
node.next=null
三、单链表的增删改查(有虚拟头节点)
虚拟头节点:只作为链表的头节点使用,不存储任何数据
3.1 头插法
当单链表不为空的情况:

当单链表为空的情况:

由以上的两个例子可以看出:有虚拟头节点之后,所有节点都是该节点的"后继"节点。无论当前是否存在有效元素,我们的插入步骤完全—致。省去了判断头节点是否为空的情况
public class LinkedLIstWithHead {
int size;
//每次实例化都链表,都实际存在的虚拟头节点
Node dummyHead =new Node();
class Node{
int val;
Node next;
public Node() {
}
public Node(int val) {
this.val = val;
}
public Node(int val, Node next) {
this.val = val;
this.next = next;
}
}
/**
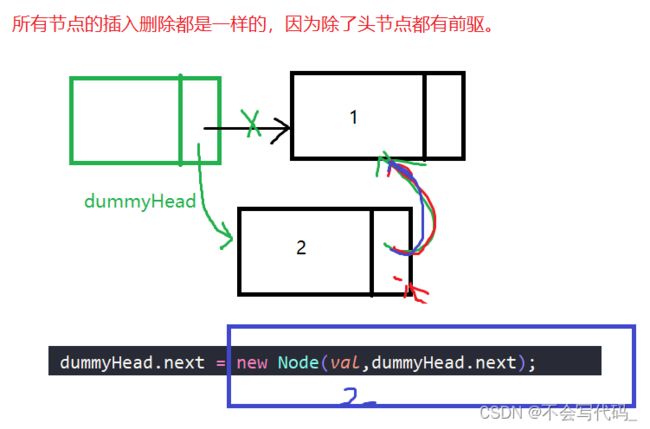
* 带虚拟头节点的头插法
* @param val
*/
public void addFirst(int val){
//1
// Node node=new Node(val,dummyHead.next);
// dummyHead.next=node;
//2
dummyHead.next=new Node(val,dummyHead.next);
size++;
}
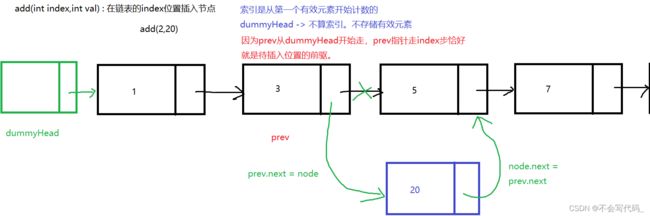
3.2 在index位置插入元素
/**
* 在index位置插入元素val
* @param index
* @param val
*/
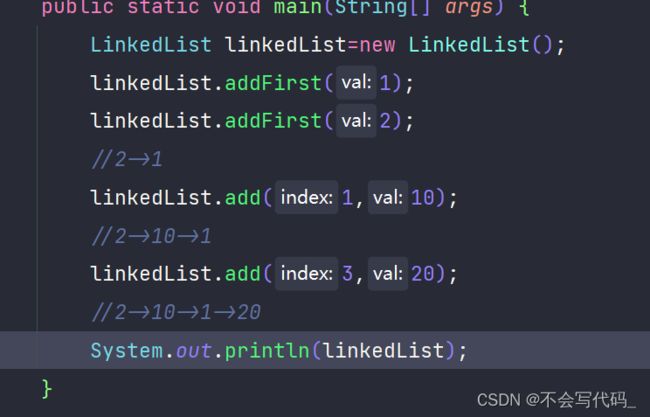
public void add(int index,int val){
if(index<0||index>size){
System.err.println("index is illegal");
return;
}
Node prev=dummyHead;
for (int i = 0; i < index ; i++) {
prev=prev.next;
}
//此时prev位于待插入位置的前驱
//1
prev.next=new Node(val,prev.next);
size++;
//2
// Node node=new Node(val, prev.next);
// prev.next=node;
}
3.3 删除index位置的元素
/**
* 删除index位置元素,并返回带删除节点val值
* @param index
* @return
*/
public int remove(int index){
//判断索引合法性
if(rangeCheck(index)){
Node prev=dummyHead;
for (int i = 0; i < index ; i++) {
prev=prev.next;
}
//cur就是待删除节点
Node cur=prev.next;
prev.next= cur.next;
int val= cur.val;
cur.next=null;
cur=null;
size--;
return val;
}
System.err.println("index is illegal");
return -1;
}
四、链表面试题
4.1快慢指针I
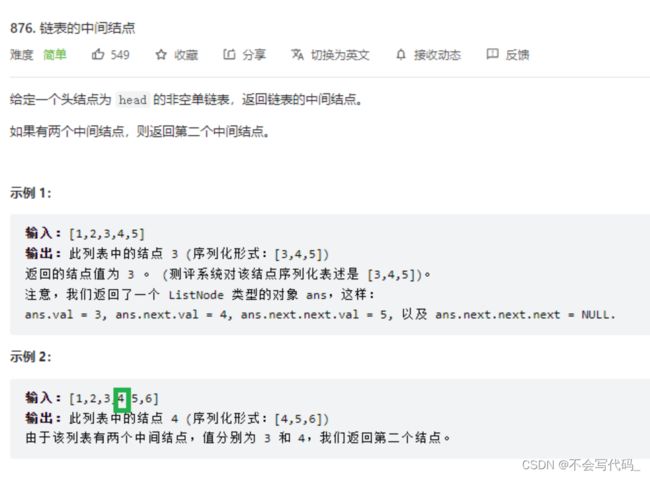
无论是奇数个还是偶数个节点,长度/2的得到的都是中间节点,只需要遍历两次链表即可返回中间节点。第一次遍历记录链表长度,第二次遍历长度/2

public ListNode middleNode(ListNode head) {
if (head == null || head.next == null) {
return head;
}
int count = 0;
//遍历链表
for (ListNode x = head; x != null; x = x.next) {
count++;
}
//中间节点从头开始遍历
ListNode middle=head;
int middleIndex=count/2;
for (int i = 0; i < middleIndex; i++) {
middle=middle.next;
}
return middle;
}
}
快慢指针:
易错点:一定要保证快指针不为空且快指针下一个节点不为空(要用&&而不是||),否则会出现空指针异常!

/**
* @author hide_on_bush
* @date 2022/9/14
*/
public class Num876_middleNode {
public ListNode middleNode(ListNode head) {
if(head==null||head.next==null){
return head;
}
ListNode low=head;
ListNode fast=head;
while (fast!=null&&fast.next!=null){
low=low.next;
fast=fast.next.next;
}
return low;
}
}
快慢指针II
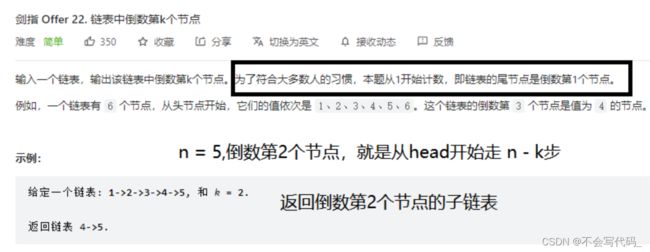
fast引用先走k步,保证和low指针之间的距离为k步,当fast走到空时和low的相对距离依旧是k,那么此时fast也走到了末尾,从后往前low就停留在了倒数第k的位置

代码中一定要让快慢指针之间的距离保持在k才可以移动慢指针,不能在if语句中快慢指针的距离为k时就移动慢指针
/**
* @author hide_on_bush
* @date 2022/9/14
*/
public class Offer21 {
public ListNode getKthFromEnd(ListNode head, int k) {
if(head==null||k<=0){
return null;
}
ListNode fast=head;
ListNode low=head;
int count=0;
while (fast!=null){
fast=fast.next;
count++;
//易错点:要等快慢指针距离保持在k,慢指针才可以移动
if(count>k){
low=low.next;
}
}
return low;
}
}
快慢指针III

回文链表:不管反转后遍历,还是正向遍历,节点完全相同。不过反转后的链表需要新建,否则原链表就丢失了

/**
* @author hide_on_bush
* @date 2022/9/15
*/
public class Nun234_isPail {
public boolean isPalindrome(ListNode head) {
ListNode newHead=reverseLinked(head);
//遍历原链表和反转后的链表,如果没有找到反例则为回文链表
while (head!=null){
if(head.val!=newHead.val){
return false;
}
head=head.next;
newHead=newHead.next;
}
return true;
}
/**
* 反转链表 - 新建链表 - 头插法
* 头插后的新链表恰好是反转后的链表
* @param head
* @return
*/
public ListNode reverseLinked(ListNode head){
ListNode dummyHead=new ListNode();
for (ListNode x=head;x!=null;x=x.next){
dummyHead.next=new ListNode(x.val,dummyHead.next);
}
return dummyHead.next;
}
}
进阶
O(1)空间复杂度代表不可以创建新链表。上面的解法创建了一个新的链表,长度就是原链表长度n,空间复杂度是O(n)

1.找到中间节点(快慢指针)
2.反转中间节点之后的链表(reverse方法)
3.同时遍历前半部分未反转链表和后半部分反转后的链表

/**
* @author hide_on_bush
* @date 2022/9/15
*/
public class Num234_isPails {
public boolean isPalindrome(ListNode head) {
ListNode midHead=middle(head);
ListNode reverseHead=reverse(midHead);
//反转链表后,前半段的链表依旧连接在反转链表后的尾结点
while (reverseHead!=null){
if(head.val!=reverseHead.val){
return false;
}
head=head.next;
reverseHead=reverseHead.next;
}
return true;
}
/**
* 快慢指针寻找链表中间节点
* @param head
* @return
*/
public ListNode middle(ListNode head){
ListNode fast=head;
ListNode low=head;
while (fast!=null&&fast.next!=null){
fast=fast.next.next;
low=low.next;
}
return low;
}
/**
* 反转链表 - 递归求解
* @param head
* @return
*/
public ListNode reverse(ListNode head){
if(head==null||head.next==null){
return head;
}
ListNode oldHeadNext=head.next;
ListNode newHead=reverse(head.next);
oldHeadNext.next=head;
head.next=null;
return newHead;
}
}
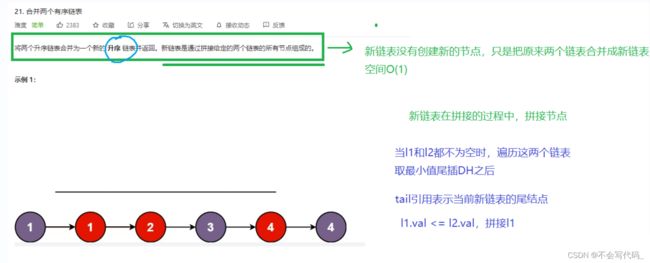
4.2合并链表
**
* @author hide_on_bush
* @date 2022/9/15
*/
public class Num21_MergeList {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
//1.判空
if(list1==null){
return list2;
}
//不可以使用else if是因为可能存在两个链表都为空的可能性
if(list2==null){
return list1;
}
ListNode dummyHead=new ListNode();
ListNode tail=dummyHead;
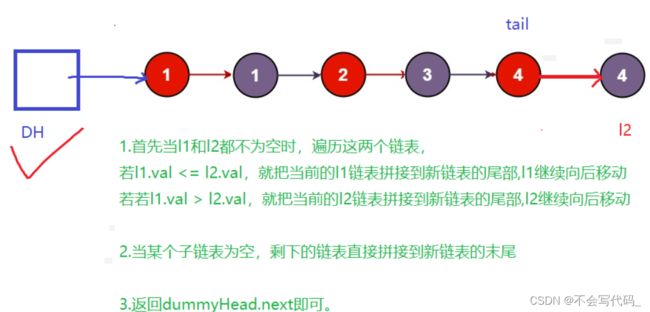
//当两个链表都不为空时,同时遍历两个链表
while (list1!=null&&list2!=null){
if(list1.val<=list2.val){
//尾插法
tail.next=list1;
tail=tail.next;
list1=list1.next;
}else {
tail.next=list2;
tail=tail.next;
list2=list2.next;
}
}
//此时说明l1或者l2遍历结束,引用走到空的位置
if(list1==null){
tail.next=list2;
}
if(list2==null){
tail.next=list1;
}
return dummyHead.next;
}
}
递归
/**
* 传入两个链表的头节点,就能合并成一个升序链表
* @author hide_on_bush
* @date 2022/9/15
*/
public class Num21_mergeLists {
public ListNode mergeTwoLists(ListNode list1, ListNode list2) {
//1.边界条件
if(list1==null){
return list2;
}
if(list2==null){
return list1;
}
//2.根绝语义,处理头节点
//两个链表头节点val值小的就是新链表的头节点
if(list1.val<=list2.val){
list1.next=mergeTwoLists(list1.next,list2);
return list1;
}else {
list2.next=mergeTwoLists(list1,list2.next);
return list2;
}
}
}
分割链表
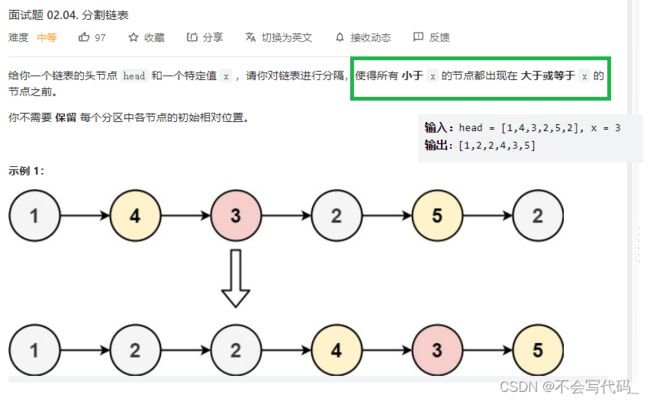

大链表和小链表最后还需要断开引用,但是小链表最后需要拼接大链表,所以省去了断引用的操作

/**
* @author hide_on_bush
* @date 2022/9/15
*/
public class Partition {
public ListNode partition(ListNode head, int x) {
//保存小于x节点的链表
ListNode smallHead=new ListNode();
ListNode smallTail=smallHead;
//保存大于等于x节点的链表
ListNode bigHead=new ListNode();
ListNode bigTail=bigHead;
//遍历原链表
while (head!=null){
if(head.val<x){
smallTail.next=head;
smallTail=smallTail.next;
}else {
bigTail.next=head;
bigTail=bigTail.next;
}
head=head.next;
}
//易错点,最后一个引用要断开
bigTail.next=null;
smallTail.next=bigHead.next;
return smallHead.next;
}
}
4.3 相交链表

相交:两个链表从某个节点开始之后的所有链表不仅val相同,next也相同,节点需要完全相同

路径问题:a+c+b=b+c+a
终止循环的条件就是l1和l2相等时,即使不相交他们走的路程相同也会同时走到null,返回null即可

/**
* @author hide_on_bush
* @date 2022/9/16
*/
public class Num160_getInsertion {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
//l1和l2分别从两个链表头节点开始遍历
ListNode l1=headA;
ListNode l2=headB;
//终止条件
//相交时:返回相交节点
//不相交时:同事走到null,返回null即可
while (l1!=l2){
l1=l1==null?headB:l1.next;
l2=l2==null?headA:l2.next;
}
return l1;
}
}
4.4 环形链表I
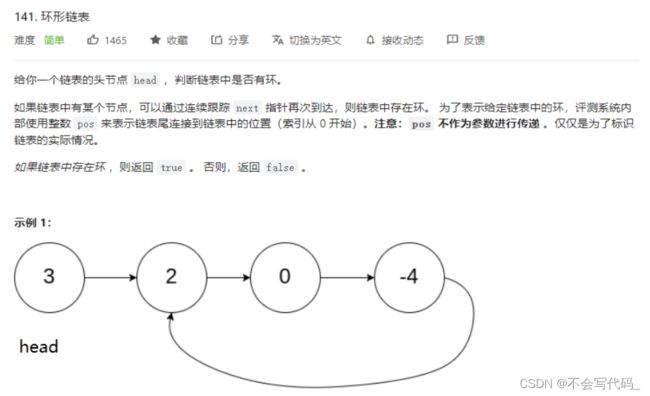
跑圈:跑的快的引用迟早可以追上跑的慢的引用,如果是一条直线,则不构成环形,并且跑得快的引用会走到null

/**
* @author hide_on_bush
* @date 2022/9/16
*/
public class Num141_hasCycle {
public boolean hasCycle(ListNode head) {
//空链表或者单个节点都不能构成环形链表
if(head==null||head.next==null){
return false;
}
ListNode fast=head.next;
ListNode low=head;
while (fast!=null&&fast.next!=null){
//快指针在环形链表中一定能和慢指针相遇
fast=fast.next.next;
low=low.next;
if(fast==low){
return true;
}
}
//快指针走到null说明次链表一定不是环形
return false;
}
}
4.5 环形链表II(数学分析)

数学分析:快慢指针在环形中相遇,设未成环的链表长度为a,环的入口到快慢指针相遇点的距离为b,相遇点剩下到环入口的距离为c。由物理的路径问题我们可以知道,相同时间内,快指针走过的路程是慢指针的2倍,快指针走过的路程设为:a+n(b+c),慢指针走过的路程设为a+b,在由物理公式化简:a+n(b+c)+b=2(a+b),令n=1可以得到关系式:a=c
/**
* @author hide_on_bush
* @date 2022/9/16
*/
public class Num142_detectCycle {
public ListNode detectCycle(ListNode head) {
//边界:不构成环
if(head==null||head.next==null){
return null;
}
//快慢指针相遇问题
ListNode fast=head,low=head;
while (fast!=null&&fast.next!=null){
fast=fast.next.next;
low=low.next;
//快慢指针相遇点
//能相遇说明一定带环
if(fast==low){
//引入第三个指针从头开始遍历
ListNode third=head;
while (third!=low) {
third = third.next;
low = low.next;
}
//此时一定位于环入口
return third;
}
}
//此时快慢指针未相遇,不构成环,并且快指针走到null
return null;
}
}
4.6 删除重复元素I
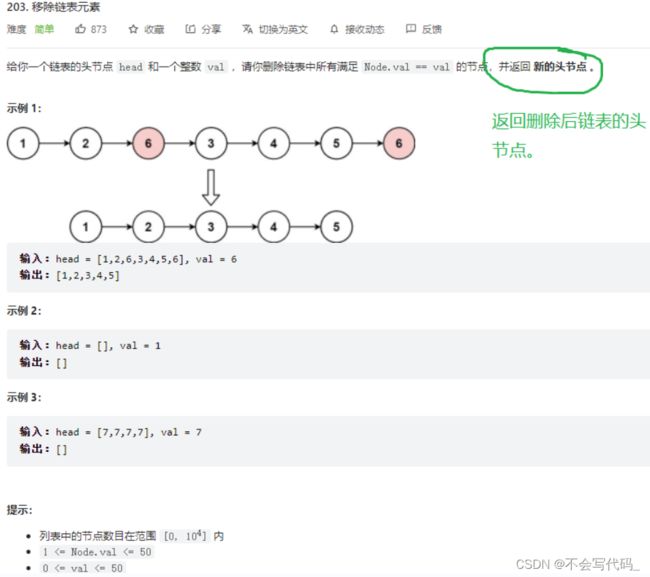
解析:while循环语句中一定要先判空,否则可能出现空指针异常



/*
* @author hide_on_bush
* @date 2022/9/12
*/
public class Num203_removeAllElements {
public ListNode removeElements(ListNode head, int val) {
//处理头结点
while(head!=null&&head.val==val){
//刷题中不需要考虑内存释放问题
head=head.next;
}
//特殊情况处理
//可能出现全部节点都是重复元素
if(head==null){
return null;
}else {
//头节点不为空且不是待删除元素
ListNode prev=head;
while (prev.next!=null){
if(prev.next.val==val){
ListNode cur=prev.next;
prev.next=cur.next;
}else{
prev=prev.next;
}
}
return head;
}
}
}
递归求解
public ListNode removeElements(ListNode head, int val) {
if (head == null) {
return null;
}
//将头节点之后的节点交给子函数处理
head.next = removeElements(head.next, val);
//处理头结点
return head.val==val?head.next:head;
}
带虚拟头节点解法
//带虚拟头节点解法
public ListNode removeElements(ListNode head, int val) {
ListNode dummyHead = new ListNode();
dummyHead.next = head;
ListNode prev = dummyHead;
while (prev.next != null) {
if (prev.next.val == val) {
prev.next = prev.next.next;
} else {
prev = prev.next;
}
}
return dummyHead.next;
}
}
4.7 删除重复元素II
/**
* @author hide_on_bush
* @date 2022/9/13
*/
public class Num83_removeAllElements {
public ListNode deleteDuplicates(ListNode head) {
//边界条件
if (head == null || head.next == null) {
return head;
}
//三引用
ListNode dummyHead = new ListNode();
dummyHead.next = head;
ListNode prev = dummyHead;
//用来和next引用对比是否val相同
ListNode cur = head;
//cur遍历完链表所有节点就结束了
while (cur != null) {
//每次要更新next引用位置
ListNode next = cur.next;
while (next != null && next.val == cur.val) {
next = next.next;
}
//此时next一定走到与cur.val不相同的元素
cur.next = next;
cur = next;
next = null;
}
return head;
}
}
递归解法:
//递归
// 传入一个链表的头节点,返回删除重复元素后的链表头节点,并且重复元素只保留一个
//1.边界条件,递归重点
if (head == null||head.next==null) {
return head;
}
//2.子链表交给子函数处理
head.next = deleteDuplicates(head.next);
//3.处理头结点
if(head.val==head.next.val){
return head.next;
}else {
return head;
}
}
4.8 删除重复元素III(面试重点)

当cur.val和next.va不相等时,prev是不一定能向后移动的,可能出现连续两个不同的重复元素

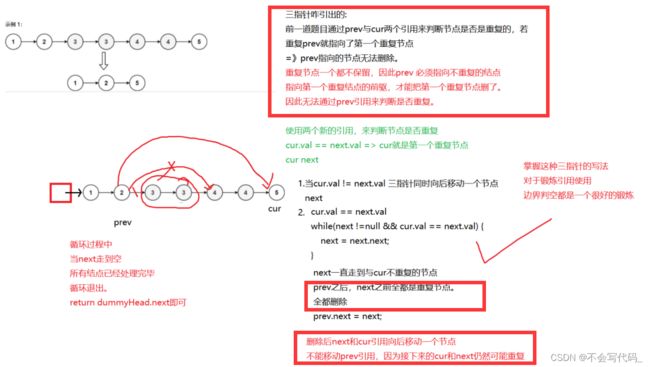
/**
* @author hide_on_bush
* @date 2022/9/13
*/
public class Num82_removeAllElements {
public ListNode deleteDuplicates(ListNode head) {
//不需要判空,根据题意得知
ListNode dummyHead=new ListNode();
ListNode prev=dummyHead;
dummyHead.next=head;
ListNode cur=head;
while (cur!=null){
ListNode next=cur.next;
//说明next已经走到末尾,直接返回头节点
//或者链表中只有一个节点
if(next==null){
break;
}else {
//此时cur一定不是待删除元素,可以移动prev
if(cur.val!=next.val){
prev=prev.next;
cur=cur.next;
}else {
while (next!=null&&cur.val==next.val){
next=next.next;
}
prev.next=next;
cur=next;
//易错点
//此时不移动prev节点是因为虽然cur和next值不相等
//但无法保证next的位置是否是待删除节点
}
}
}
return dummyHead.next;
}
}
递归解法
public static ListNode deleteDuplicates(ListNode head) {
//1.边界
if (head == null || head.next == null) {
return head;
}
//2.判断头结点是不是待删除节点
//题目要求重复元素一个不留
if (head.value == next.value) {
//处理头结点,保证头节点一定不是重复元素
ListNode next = head.next;
while (next != null && head.value == next.value) {
next = next.next;
}
return deleteDuplicates(next);
} else {
//头节点不是重复元素,直接将子链表交给子函数处理
head.next = deleteDuplicates(next);
return head;
}
}
4.9 反转链表I
解法一:若不要求空间复杂度为O(1)可以直接构建新链表,边遍历原链表边头插创建新链表
/**
* 传入一个链表的头节点,返回反转后的链表头结点
* @author hide_on_bush
* @date 2022/9/14
*/
public class Num206_reverseLinkedList {
public ListNode reverseList(ListNode head) {
//1.边界条件
if(head==null||head.next==null){
return head;
}
ListNode prev=null;
ListNode cur=head;
//2.cur遍历原链表,走到null即遍历完原链表
while (cur!=null){
//暂存cur.next,否则当链表节点反转后,找不到原链表的next节点
ListNode next=cur.next;
cur.next=prev;
prev=cur;
cur=next;
}
//3.prev恰好走到新的头节点
return prev;
}
}
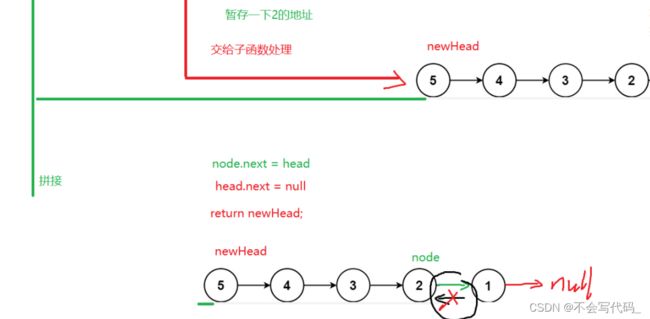
递归解法
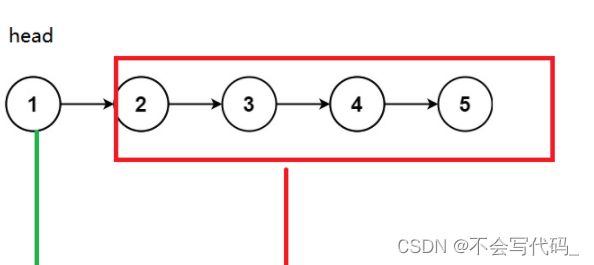
易错点:
1.保存原链表head.next
2.拼接原头节点时,不能忘记把原头节点next引用指向null,否则和子链表尾节点形成环形
public ListNode reverseList(ListNode head) {
//1边界条件
if(head==null||head.next==null){
return head;
}
//2处理头节点
//暂存原链表的head.next,便于子函数处理完链表后拼接
ListNode oldHeadNext=head.next;
//子链表头节点,也就是原链表尾结点
ListNode newHead=reverseList(head.next);
//拼接头节点
oldHeadNext.next=head;
//隐藏的易错点:原链表头节点next还指向原链表的head.next
head.next=null;
return newHead;
}
}
4.10 反转链表II
/**
* @author hide_on_bush
* @date 2022/9/16
*/
public class Num92_reverseList {
public ListNode reverseBetween(ListNode head, int left, int right) {
//边界条件
if(head==null||head.next==null){
return head;
}
//保证前驱节点是待反转节点前驱
ListNode dummyHead=new ListNode();
dummyHead.next=head;
ListNode prev=dummyHead;
//走left-1到待反转前驱
for (int i = 0; i <left-1 ; i++) {
prev=prev.next;
}
ListNode cur=prev.next;
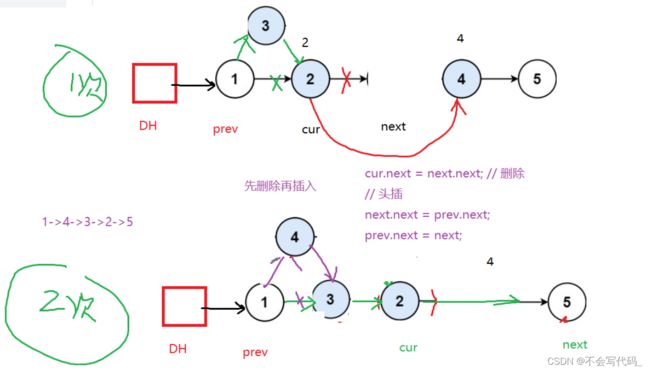
//反转+头插
for (int i = 0; i < right-left ; i++) {
//下一个要处理的节点
ListNode next=cur.next;
cur.next=next.next;
//头插
next.next=prev.next;
prev.next=next;
}
return dummyHead.next;
}
}
五、双向链表
public class DoubleLinkedList {
// 有效节点的个数
private int size;
// 当前头节点
private DoubleNode head;
// 当前尾节点
private DoubleNode tail;
// 双向链表的节点类
}
class DoubleNode {
// 前驱节点
DoubleNode prev;
// 当前节点值
int val;
// 后继节点
DoubleNode next;
// alt + insert
public DoubleNode() {}
public DoubleNode(int val) {
this.val = val;
}
public DoubleNode(DoubleNode prev, int val, DoubleNode next) {
this.prev = prev;
this.val = val;
this.next = next;
}
}
6.1头插法
public void addFirst(int val) {
// 首先创建一个新节点
// 这个新节点就是以后的头节点
// 构造方法就是为对象属性进行初始化的!
DoubleNode node = new DoubleNode(null,val,head);
if (tail == null) {
tail = node;
}else {
head.prev = node;
}
// 对于头插来说,最终无论链表是否为空。head = node
//重复代码
head = node;
size ++;
}
6.2尾插法
public void addLast(int val) {
// 这个节点就是插入后的尾节点
DoubleNode node = new DoubleNode(tail,val,null);
if (tail == null) {
head = node;
}else {
tail.next = node;
}
tail = node;
size ++;
}
6.3根据索引插入节点(中间位置插入)

新插入的节点可以在创建对象时使用构造方法,再把前驱节点的next和后继节点的prev连接上就完成了插入。
/*
* 根据索引插入节点
* */
public void add(int val,int index){
//边界问题
if(index<0||index>size) {
System.err.println("index is illegal");
return;
}
//头插法
if(index==0)addFirst(val);
//尾插法
else if(index==size)addLast(val);
else {
//中间位置插入
//一个根据索引找到对应节点的方法
DoubleNode prev=node(index-1);
DoubleNode node=new DoubleNode(prev,val,prev.next);
prev.next.prev=node;
prev.next=node;
size++;
}
}
/*
* 根据索引查找节点
* */
public DoubleNode node(int index) {
if (index<size/2) {
DoubleNode x = head;
for (int i = 0; i < index; i++) {
x = x.next;
}
return x;
} else {
//索引大于链表有效节点的2分之1就从尾部开始遍历
DoubleNode x = tail;
for (int i = size - 1; i < index; i++) {
x = x.prev;
}
return x;
}
}
6.4双向链表删除(分治思想)
任意删除的节点看作两部分,先处理前驱节点,完全不管后继。等前驱节点全部处理完毕,在单独处理后继节点


第一个if else处理前驱是否为空的情况,第二个else if处理后继节点是否为空的情况。两个else if的组合情况解决四种删除情况(前空后空等)。
/*
* 分治法 解决删除节点的方法
* 两个else if拼接在一起就是我们要删除的节点
* */
public void unlink(DoubleNode node){
DoubleNode prev=node.prev;
DoubleNode successor=node.next;
//先处理前驱
if(prev==null){
//待删除元素前驱节点为空说明删除头节点
head=successor;
//后继是否为空不用关心
}else{
//如果前驱不为空,则前驱节点直接连到后继
prev.next=successor;
node.prev=null;
}
//后继节点为空说明删除尾结点
if(successor==null){
tail=prev;
}else{
//后继不为空的处理情况
successor.prev=prev;
node.next=null;
}
size--;
}
删除索引为index的节点
/*
* 删除索引为index的节点
* */
public void removeIndex(int index){
if(index<0||index>=size){
System.err.println("index is illegal");
return;
}
DoubleNode cur=node(index);
unlink(cur);
}
/*
* 删除出现了一次val值的节点
* */
public void removeValueOnce(int val){
for(DoubleNode x=head;x!=null;x=x.next){
if(x.val==val){
unlink(x);
break;
}
}
}
删除节点值为val的所有节点
/*
* 删除所有值为value的节点
* */
public void removeAllValue(int val){
for(DoubleNode x=head;x!=null;){
if(x.val==val){
//因为unlink最后把node的next置为null所以for循环
//next找不到后继节点,先创建对象保存x的后继
DoubleNode next=x.next;
unlink(x);
x=next;
}else{
//不相等的时候就for循环的++条件写在后面
x=x.next;
}
}
}