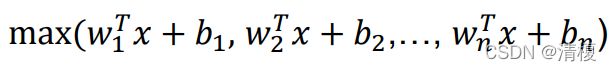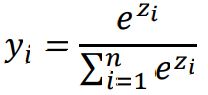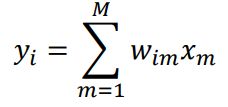卷积神经网络基础
一、卷积
本来想自己写一点,发现了很不错的一篇博客,就不班门弄斧了。
什么是卷积? - 知乎
一句话概括:某一时刻,某点的能量(或值)等于多个其他点的叠加。
二、卷积神经网络基础
CNN的核心思想
如果简单采用全连接的方式去训练模型,参数量过多难以训练,训练结束后也很容易导致过拟合,CNN能够有效的解决这一问题,其核心思想包括两点:
(1)局部连接:视觉是具有局部性的,相邻的部分点可能就构成了一个完整的物体,距离越远的点可能联系就越弱。因此因当充分考虑邻域信息,对局部的点进行稠密连接即可。
(2)权重共享:CNN中使用一组卷积核对于不同位置进行卷积,原理是每一组权重抽取图像的一种特征,例如,在抽取形状特征时可以在图像的不同位置使用同一组权重。
基于这两个关键点,CNN可以大幅减少处理图像时所需的参数量,从而减少过拟合。
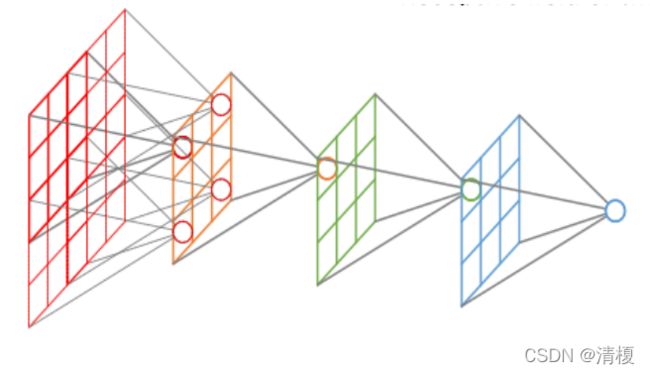
感受野
一句话:特征图上的一个点对应输入图上的区域。
如下图所示:
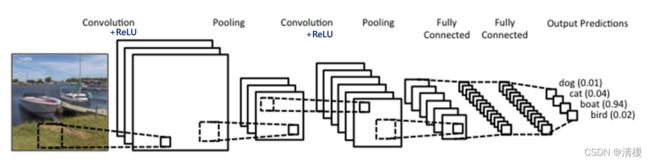
卷积神经网络结构:
- 卷积层+激活函数(Conv+ReLU)
- 池化层(Pololing)
- 全连接层(FC)
2.1 卷积层
2.1.1 卷积运算
一共四步:反转、移动、乘积、求和。
在神经网络中无需反转操作,只有三步。
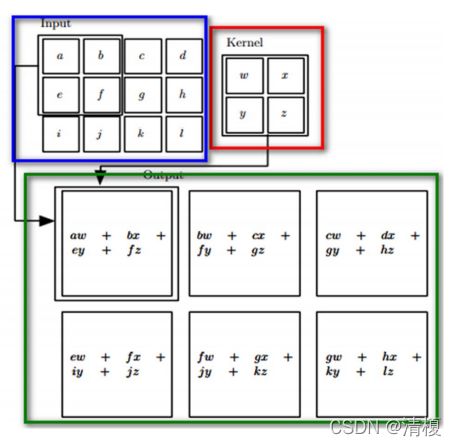
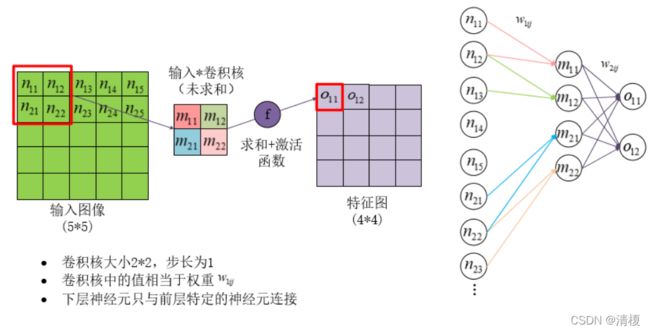
如下图所示输入矩阵I与卷积核K对应相乘,乘完后相加得到一块的值,移动步长1继续相乘相加最终得到输出矩阵。
此处可以看到的是一个3X4的矩阵做完卷积后变成了2X3的矩阵,在图像处理中即为输入图像与卷积核进行卷积后的结果中损失了部分值,输入图像的边缘被“修剪”掉了(边缘处只检测了部分像素点,丢失了图片边界处的众多信息)。这是因为边缘上的像素永远不会位于卷积核中心,而卷积核也没法扩展到边缘区域以外。
这个结果我们是不能接受的,有时我们还希望输入和输出的大小应该保持一致。为解决这个问题,可以在进行卷积操作前,对原矩阵进行边界填充(Padding),也就是在矩阵的边界上填充一些值,以增加矩阵的大小,通常都用0来进行填充的。
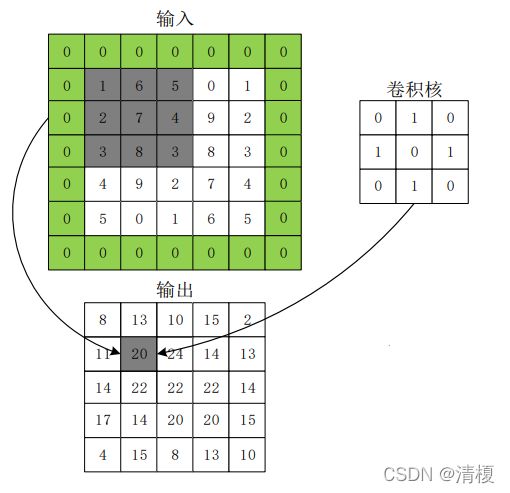
如下图所示,输入5X5,输出仍然为5X5。
步幅:对于卷积的步幅大小设计应该尽可能的让其填充后的长度除得尽。
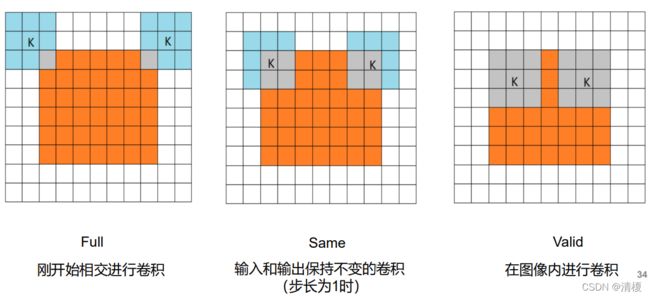
卷积的模式:Full、Same、Valid,如下图所示:
2.1.2 通道
通道(channel):一般指图像的颜色通道。
单通道图像:一般指灰度图像
多通道图像:一般指基于RGB的图像
特征图:经过卷积和激活函数处理后的图像
单通道卷积:单通道图像的卷积(单通道图像单卷积核、单通道图像多卷积核)
多通道卷积:多通道图像的卷积(多通道图像多卷积核)
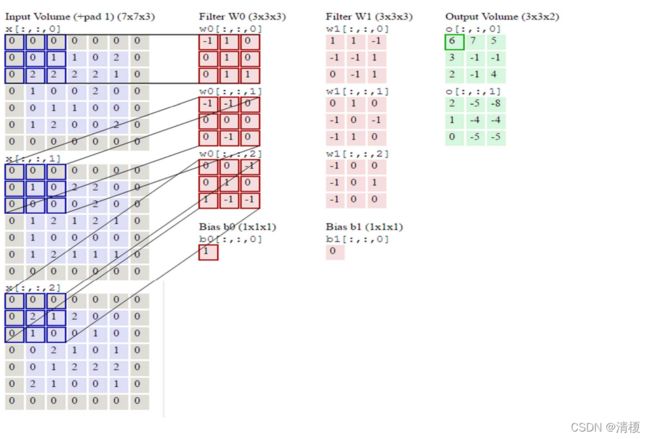
多通道卷积在计算时,输入图像和卷积核对应位置相乘再相加,然后多个卷积核的结果再进行相加,最后加上偏置即为输出特征图。如下图所示:
x[:,:,0]与w0[:,:,0]结果为4,x[:,:,1]与w0[:,:,1]结果为0,x[:,:,2]与w0[:,:,2]结果为1,再加上偏置1最后结果为9,正如o[:,:,0]所示。
2.1.3 扩张卷积
针对图像语义分割问题中下采样会降低图像分辨率、丢失信息而提出的一种卷积形式。
扩张率:卷积核处理数据时各原始值之间的距离。
利用添加空洞(空洞补0)扩大感受野,让原本3x3的卷积核,在相同参数量和计算量下拥有更大的感受野,从而无需下采样。
2.1.4 标准卷积与深度可分离卷积
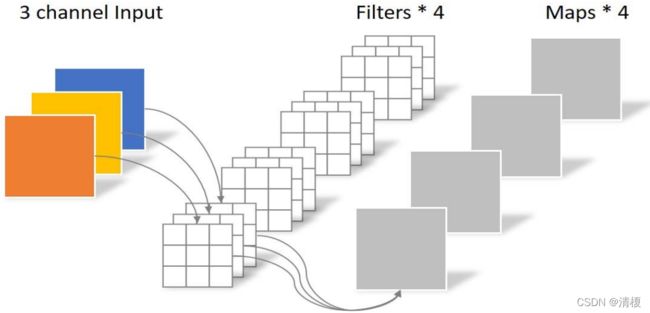
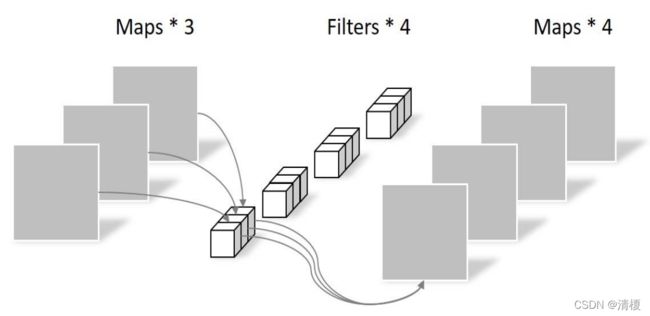
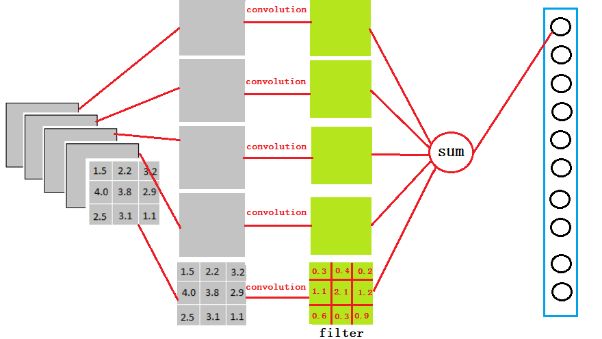
标准卷积:如下图所示,卷积层有4个Filter,每个Filter有3个卷积核,每个卷积核为3X3的,故参数总量为4X3X3X3,共108个。
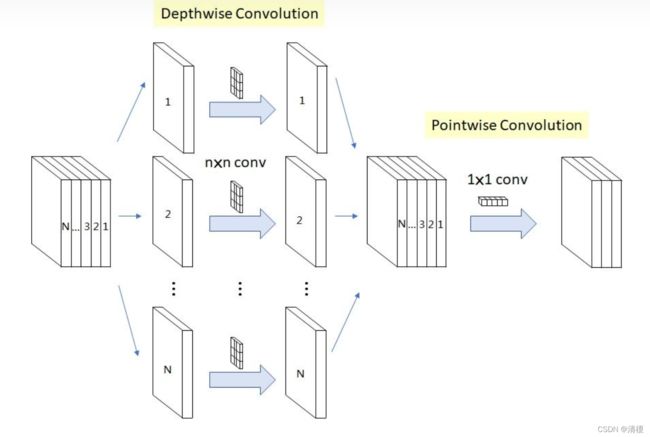
深度可分离卷积:Depthwise Separable Convolution,先做Depthwise卷积,再做Pointwise 卷 积,实现空间维(卷积核大小)和通道维(特征图)的分离。
如下图所示,DSC由Depthwise Convolution和Pointwise Convolution两部分构成。Depthwise Convolution的计算非常简单,它对channel input的每个通道分别使用一个卷积核,然后将所有卷积核的输出再进行拼接得到它的最终输出。
Pointwise Convolution实际为1×1卷积,相乘再叠加即可。
相比标准卷积参数数量大幅减少,Depthwise卷积(3X3X3=27),Pointwise(4X3X1X1=12),总共39个。
详细结束见:卷积神经网络之深度可分离卷积(Depthwise Separable Convolution) - 知乎
2.1.5 卷积层作用
浅层卷积层:提取的是图像基本特征,如边缘、方向 和纹理等特征。
深层卷积层:提取的是图像高阶特征,出现了高层语义模式, 如“车轮”、“人脸”等特征。
2.2 激活函数
常用激活函数主要有:identity、ReLU、PReLU、ERU、Maxout。
2.2.1 identity
![]()
适合线性任务,相对稳定,但是对卷积输出没有影响。
2.2.2 ReLU
ReLU函数的优点:
• 计算速度快。ReLU函数只有线性关系, 比Sigmoid和Tanh要快很多。
• 输入为正数的时候,不存在梯度消失问题。
ReLU函数的缺点:
• 强制性把负值置为0,可能丢掉一些特征。
• 当输入为负数时,权重无法更新,导致 “神经元死亡”(学习率不要太大)。
2.2.3 PReLU
当α=0.01时,称作Leaky ReLU, 当从高斯分布中随机产生时,称为 Randomized ReLU(RReLU)。
PReLU函数的优点:
• 比sigmoid/tanh收敛快。
• 解决了ReLU的“神经元死亡”问题。
PReLU函数的缺点:
• 需要再学习一个参数,工作量变大。
2.2.4 ELU
ELU函数的优点:
• 处理含有噪声的数据有优势。
• 更容易收敛(带e的求导更易收敛)。
ELU函数的缺点:
• 计算量较大,收敛速度较慢。
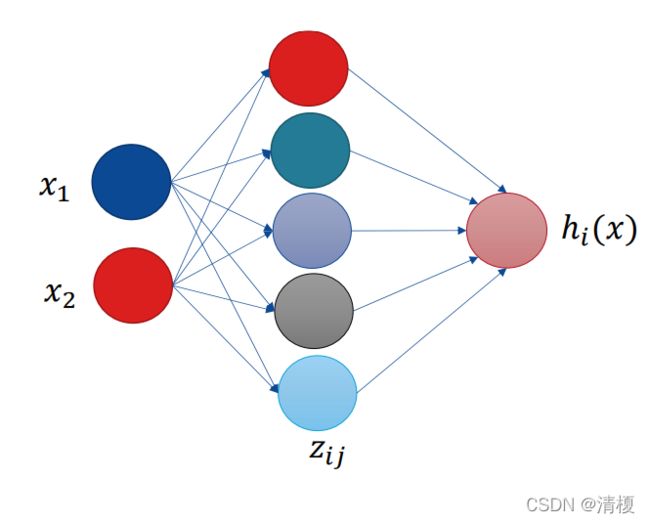
2.2.5 Maxout
增加一层神经网络,神经元个数k自定。
Maxout函数的优点:
• Maxout能够缓解梯度消失。
• 规避了ReLU神经元死亡的缺点。
Maxout函数的缺点:
• 增加了参数和计算量。
2.2.6激活函数选择
CNN在卷积层尽量不要使用Sigmoid和Tanh,将导致梯度消失。
首先选用ReLU,使用较小的学习率,以免造成神经元死亡的情况。
如果ReLU失效,考虑使用Leaky ReLU、PReLU、ELU或者 Maxout,此时一般情况都可以解决。
2.3 池化层
在 CNN中,通常会在连续的 Conv 层之间定期插入一个池化层。其功能是缩小特征图尺寸,以减少网络中的参数和计算量,从而控制过拟合。池化层无包含需要训练的参数,指定池化的大小、步幅、类型即可。同时由于池化层取了多个位置的总体统计特征,增加了网络的鲁棒性。
池化操作使用某位置相邻输出的总体统计特征作为该位置的输出。
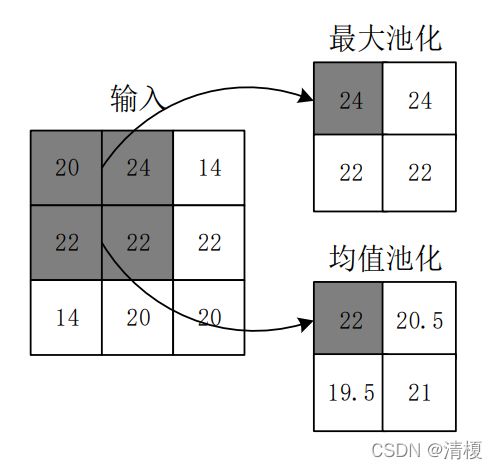
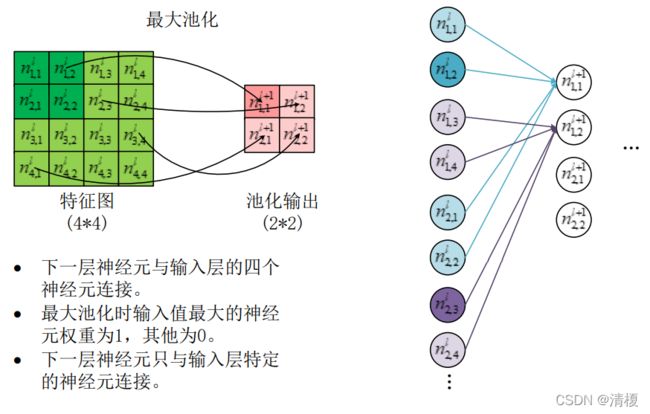
常用最大池化(max-pooling)和 均值池化(average-pooling),如下图所示,其中最大池化使用较多。
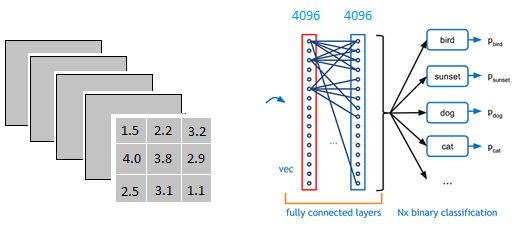
2.4 全连接层
以上图为例,我们仔细看上图全连接层的结构,全连接层中的每一层是由许多神经元组成的(1x 4096)的平铺结构。
问题来了,3X3X5的输出又是怎么变到1X4096的呢?
可以理解为做了一个卷积,从上图我们可以看出,我们用一个3x3x5的filter 去卷积激活函数的输出,得到的结果就是一个fully connected layer 的一个神经元的输出,这个输出就是一个值。
因为我们有4096个神经元
实际上我们就是用一个3x3x5x4096的卷积层去卷积激活函数的输出
这么做又有什么用呢?
在2.2中提到过,卷积层的作用是提取特征,到全连接层时特征已经提取完了,现在要做的是分类。
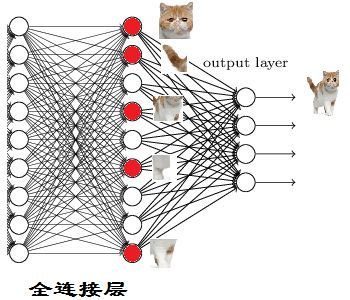
从后往前进行推,如果要识别一只修猫, 红色表示神经元被激活了,将这些特征组合到一起就可识别为猫。
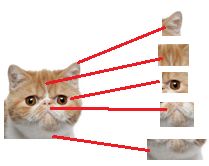
往前继续推,一只猫猫头又有多个特征,眼睛、耳朵、嘴巴等,组合可以识别出猫头。
这细节特征又是怎么来的?
就是从前面的卷积层,下采样层来的,这样一来就串起来了。
参考:CNN 入门讲解:什么是全连接层(Fully Connected Layer)? - 知乎 (zhihu.com)
2.5 输出层
2.5.1 分类问题
对于分类问题使用Softmax函数。
其中Zi为第i个节点的输出值,n为输出节点的个数,即分类的类别个数。通过Softmax函数就可以将多分类的输出值转换为范围在[0, 1]和为1的概率分布。
Softmax的意义在于不再唯一的确定某一个最大值,而是为每个输出分类的结果都赋予一个概率值,表示属于每个类别的可能性。
2.5.2 递归问题
对于递归问题使用线性函数。
2.6 卷积神经网络的训练
步骤:
Step 1: 用随机数初始化所有的卷积核和参数/权重。
Step 2: 将训练图片作为输入,执行前向步骤(卷积,ReLU,池化 以及全连接层的前向传播)并计算每个类别的对应输出概率 。
Step 3: 计算输出层的总误差:总误差=1/2 ∑ (目标概率−输出概 率)^2。
Step 4: 使用BP算法计算误差相对于所有权重的梯度,并用梯度下降法更新所有的卷积核/权重和参数的值,以使输出误差最小 。
卷积层和池化层在训练时要改成神经网络的形式,如下图所示