【算法总结】双指针 (快慢指针、滑动窗口、对撞指针)

最近刚开始在leetcode上刷题，最开始也是从数组、双指针、二分查找这类相对来说简单的题型进行入手的。我主要刷的是一些简单和中等题目因为每天时间也是很有限。

那么此篇主要是总结以下关于双指针这类题型的算法。这里的双指针的c语言里的双指针并不是一个东西，这里的指针指的是数组下标，我们具象的成为指针，实际上就是利用这些索引的移动能够达到类似指针的作用。我这里主要用c++实现

tips:如果大家需要算法相关的博客 代码，及leetcode一些c++的解法题目可以来我的 github自取 https://github.com/ChengxuLee/struct
虽然内容不算特别全 但也是根据小白的刷题顺序来进行的 每天不断更新以简单中等题为主。

双指针题型大致分为以下几种：

• 快慢指针
• 对撞指针
• 两数组指针
• 滑动窗口

一般双指针类型的题目主要存在于数组，字符串，链表居多。接下来我将每种类型分别进行归纳总结并拿出相关例题进行分析，但不可能每种类型记住了模板就一定会做了，因此我个人还是建议记住做题解法顺序。具体题目具体分析比较好。

双指针的题一般题目中会写到：不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。

1、快慢指针

1、第一种算法常常需要将快慢指针先置为0；然后快指针的作用是遍历数组，慢指针用于交换赋值等。

例如：leecode 27 题 删除指定元素

给你一个数组 nums 和一个值 val，你需要 原地 移除所有数值等于 val 的元素，并返回移除后数组的新长度。
不要使用额外的数组空间，你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。

输入：nums = [3,2,2,3], val = 3
输出：2, nums = [2,2]

这道题是比较经典的双指针问题，一般来说最简单的办法肯定是直接调用库函数例如c++直接remove掉，或是js可以先indexOf找到位置再slice截取。但是我觉得既然是刷算法题当然是锻炼脑力以及思维能力，如果一概用库函数耍赖皮对自己来说提高并不会很明显，事实上leecode上能用库函数解决且容易想到的题并不少。但不用库函数解决的题才真是少之又少，这对于将来面试也是有好处的。

那么接下来就用双指针来详解一下：

解题思路是：将所有不等于 val 的元素移动到最前面。最后slow指向的位置**+1**就是新数组的长度。如：[3,3,2,2]

具体分析如下图所示，因为需要找到所有可以匹配的项，因此无论算法多么精妙遍历一遍数组是必不可少的，这里 fast指针的作用就是遍历数组和与 val进行比较 (即判定条件)。然后使用慢指针 slow来进行赋值，这里就要搞清楚 slow在什么情况会++ 即判定条件。

当快指针在不断向前走时，如果遇到了与 val不相等的元素那么就意味着这个数值应该是放在数组前面，或是说将其与前面等于 val的元素进行赋值，这样就可以保证所有 不等于val的元素在数组前面，即后面的元素就被剔除掉了。

因此 当nums[fast]==val时，指针直接++ 略过该元素 ，当 nums[fast]!=val 时 将slow位置的元素值改为fast位置的值（这里slow的值已经被fast检测过了因此一定是==val的值）。遍历到fast到最后也就是 nums.length()-1结束。

class Solution {
public:
    int removeElement(vector<int>& nums, int val) {
        int slow=0,fast=0;
       for(fast=0;fast<nums.size();fast++){ //可以使用while 循环 fast用于遍历数组 和与 val对比
           if(nums[fast]!=val){
               nums[slow]=nums[fast]; //当赋值后 慢指针需要++ 这也是最后返回长度不需要+1的原因
               slow++;
           }
       }
        return slow; //返回值不需要+1 因为最后一次遍历后 slow指针已经又一次++了
    }
    };

这种算法的时间复杂度是 O（n）空间复杂度在常量 O（1）。这种与暴力解法的效率更高，暴力解法时间复杂度通常在O（n^2）

而且做算法题如果都用暴力求解意义不大

2、第二种算法就是链表上是否有环的判断（不限于链表），这种常规是快指针跳两步，慢指针跳一步 如果有环一定会相遇

例如：leetcode 202快乐数

编写一个算法来判断一个数 n 是不是快乐数。

「快乐数」 定义为：

对于一个正整数，每一次将该数替换为它每个位置上的数字的平方和。
然后重复这个过程直到这个数变为 1，也可能是 无限循环 但始终变不到 1。
如果这个过程 结果为 1，那么这个数就是快乐数。
如果 n 是 快乐数 就返回 true ；不是，则返回 false 。

输入：n = 19
输出：true
解释：
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1

这道题的思路在于无限循环和等于1的判断，如下图所示快指针每次跳两步，慢指针每次跳一步。无论如何二者皆会有相遇之时，因此只需要判断相遇时的值是否等于一即可。以下是通过链表实现的，即判断链表是否有环

class Solution {
public:
    int bitSquareSum(int n) {
        int sum = 0;
        while(n > 0)
        {
            int bit = n % 10; // 计算结果
            sum += bit * bit;
            n = n / 10;
        }
        return sum;
    }
    
    bool isHappy(int n) {
        int slow = n, fast = n;
        do{
            slow = bitSquareSum(slow);//慢指针跳一次
            fast = bitSquareSum(fast);//快指针跳两次
            fast = bitSquareSum(fast);
        }while(slow != fast);
        
        return slow == 1;
    }
};

类似的题还有 leetcode 876. 链表的中间结点 等 都是利用了 快指针跳两次 慢指针跳一次，如有环 终会相遇的原理

2、对撞指针

顾名思义对撞指针的意思就是两个指针在数组两头，快慢指针是在同一边有明显的区别。第二点就是对撞指针通常是区间慢慢变小，即 l++ 和 r–。 如下图所示：求数组内等与 target值的数组下标。

解题思路：左右各一个指针，如果两个值大于target 则右指针–，如果小于target 则左指针++ 因为数组是正序的所以可以这样操作

例如：leetcode 167两数之和2

给你一个下标从 1 开始的整数数组 numbers ，该数组已按 非递减顺序排列 ，请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ，则 1 <= index1 < index2 <= numbers.length 。

以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。

你可以假设每个输入 只对应唯一的答案 ，而且你 不可以 重复使用相同的元素。

你所设计的解决方案必须只使用常量级的额外空间。

输入：numbers = [2,7,11,15], target = 9
输出：[1,2]

如上所用办法可以得出以下解法：

class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
         int l=0;int r=numbers.size()-1; int sum;
         vector <int> a;
         while(l<r){
            sum=numbers[l]+numbers[r];
             if(sum==target){ //相等则 导入到新容器 
                 a.push_back(l+1);
                 a.push_back(r+1);
                 return a;
             }else if(sum<target){ //小于目标值 则左指针++
                 l++;
             }else{    //大于目标值 则右指针--
                 r--;
             }
         }
            return numbers;
    }
};

例如：leetcode 11盛水最多的容器

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

如题意可以得出以下结论：

1、无论是哪两个数据都要以最低的数值为基准，即高度

2、长度是两个值下标的差值+1

3、以左面的数据为准来看，只有长度达到最右侧宽度才能达到最大值，从右面看最左侧宽度才是最大值

4、以上几条可得，我们每次需要选择更短 的柱子进行替换，即 左面柱子长则 右指针–，如果左面柱子短 则左指针++，然后选择面积更大的值

class Solution {
public:
    int maxArea(vector<int>& height) {
        int front=0,rear=height.size()-1;
        int maxarea=0;int area=0;
        while(front<rear){
            area = min(height[front], height[rear]) * (rear - front);
            if(height[front]<height[rear]){ // 右高则做继续++
                front++;
            }else{
                rear--;						//做高则做继续右--
                }
            maxarea=max(area,maxarea);  //找到最大值
            }
            return maxarea;
    }
};

3、两数组指针

这种解法通常是给出两个数组其实原理和对撞指针，快慢指针结合比较像，只是将左右指针放在了两个数组。

leetcode 349 两个数组的交集

给定两个数组 nums1 和 nums2 ，返回 它们的交集 。输出结果中的每个元素一定是 唯一的。我们可以 不考虑输出结果的顺序 。

输入：nums1 = [1,2,2,1], nums2 = [2,2]
输出：[2]

思路是先排序保证顺序，然后再左右各一个指针当数值相同时则放入新数组

class Solution {
public:
    vector<int> intersection(vector<int>& nums1, vector<int>& nums2) {
        int f1=0;int f2=0;
        set<int>m;
        vector<int>a;
        sort(nums1.begin(),nums1.end());sort(nums2.begin(),nums2.end());
        while(f1<nums1.size()&&f2<nums2.size()){
            if(nums1[f1]==nums2[f2]){ //数值相同则放入容器 
                m.insert(nums1[f1]);
                f1++;
                f2++;
            }else if(nums1[f1]>nums2[f2]){
                 f2++;
            }else{
                 f1++;
            }
        }
         a.assign(m.begin(),m.end());
          return a;
    }
};

4、滑动窗口

• 最长区间滑动窗口

  3.无重复字符的最长子串.

  1004.最长连续1的个数

• 最短区间滑动窗口

  209.长度最小的子数组·

  76.最小覆盖子串

• 定长区间滑动窗口

  567字符串的排列
  438.找到字符串中所有字母异位词

  滑动窗口类的题目可分为以上三种，核心原理基本都是差不过，主要是改变左右指针之间的区间或定长区间来获得相关的字符串或数组。

最长区间滑动窗口

一般滑动窗口的题需要结合map来合作使用，map目的在于存储之前的数值，根据题意在滑动的过程中进行增删map里的内容，然后再进行比较找到最长的区间

leetcode 3. 无重复字符的最长子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长子串 的长度。

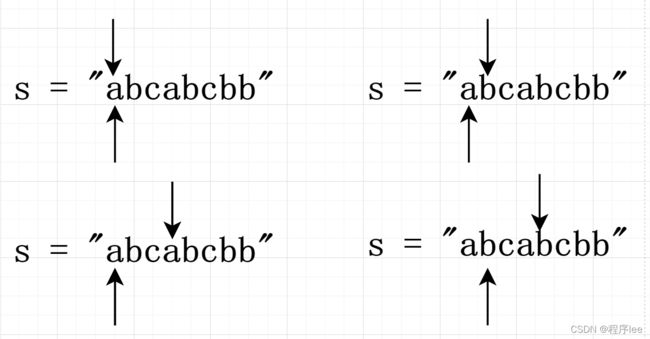
输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

首先设置一个map空间，和两个指针，左右指针的距离就是滑动窗口。每次指针滑动时便去map查找 如果存在该元素则跳过 不存在则放入 并存下字符串的（左右指针相减+1）长度。因为子串不能有重复元素因此当 有重复元素时 左指针++ （即map内存在该元素则左指针移动）

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        if(s.size() == 0) return 0;
        unordered_set<char> lookup;
        int maxStr = 0;
        int left = 0;
        for(int i = 0; i < s.size(); i++){
            while (lookup.find(s[i]) != lookup.end()){
                lookup.erase(s[left]);
                left ++;
            }
            maxStr = max(maxStr,i-left+1);
            lookup.insert(s[i]);
    }
        return maxStr;
        
    }
};

最短区间滑动窗口

一般题目中有最长，最短等基本就是动态规划或双指针题目。和最长区间差不多，需要左右指针，通常也可以与map相结合或单独使用。

leetcode 209. 长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, …, numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

依题目所得我们需要找到>=target 的长度最小的子数组，那么可以使用双指针进行解决，左指针与右指针指向第一个元素。进行遍历，右指针的作用依旧是遍历数组，左右指针区间内的和如果>=target 则记录下该值并 收缩窗口 即左指针++ 小于 target则右指针++扩展窗口

class Solution {
public:

    int minSubArrayLen(int target, vector<int>& nums) {
        int res = INT_MAX; //记录距离
        int sum = 0; 	//记录数值
        for(int i = 0, j = 0; i < nums.size(); i++)
        {
            sum += nums[i];     //向右扩展窗口
            while(sum - nums[j] >= target) sum -= nums[j++]; //向左收缩窗口
            if(sum >= target)  res = min(res, i - j + 1);    //区间更新
        }
        return res == INT_MAX ? 0 : res;                     
    }
};

定长区间滑动窗口

定长区间与以上两个有所不同，它的区间是不会反复改变的即定长。有时我们甚至只需要一个指针即可，因为区间定长我们可以立马知道另一个指针的位置。

leetcode 567. 字符串的排列

给你两个字符串 s1 和 s2 ，写一个函数来判断 s2 是否包含 s1 的排列。如果是，返回 true ；否则，返回 false 。

换句话说，s1 的排列之一是 s2 的 子串 。

输入：s1 = "ab" s2 = "eidbaooo"
输出：true
解释：s2 包含 s1 的排列之一 ("ba").

这类题型通常是在右指针++的同时左指针也++，因此可以保证窗口不变的同时数据也在更新。在左右指针++时注意 并不只是指针动就完事了 要考虑到相应的容器中的数据是否删除和增加了。

这道题就是典型的定长区间滑动窗口的题，因为s2包含s1 所以包含就必须长度一致，因此滑动窗口的长度就是 s1.length()。这道题需要两个额外容器来存储字符串的位置。如果s2中包含了s1的定长区间子串则结束 不包含则 滑动窗口改变。通过两个容器内容是否相等便可以知道s2中是否包含了s1 的子串了

class Solution {
public:
    bool checkInclusion(string s1, string s2) {
        if(s1.size()>s2.size()) return false;
        vector<int>v1(26,0);
        vector<int>v2(26,0);
        for(int i=0;i<s1.size();i++){
                   v1[s1[i]-'a']++;
                   v2[s2[i]-'a']++;
        }
        if(v1==v2) return true;
        for(int k=s1.size();k<s2.size();k++){
            v2[s2[k]-'a']++;
            v2[s2[k-s1.size()]-'a']--; //滑动窗口
            if(v1==v2) return true;
        }
        return false;
    }
};

结语：双指针类型算是比较适合入门刷题的类型，我这里整理了四种常见的类型及相关题型并没有做成模板，我认为刷题关键在于开阔思维，如果只记住一成不变的模板是没有意义的，更何况题型太多了如果到面试时没有记住模板导致自己思维又不活跃没有主动思考过其中的原理，是没必要的

关于更多的双指针类型题目可能也存在着千变万化的细节，但大体的思路总不会变，希望大家慢慢刷题在其中寻找规律