“华为杯”研究生数学建模竞赛2019年-【华为杯】D题：汽车行驶工况构建
目录
摘 要：
1.问题背景与问题重述
1.1 问题背景
1.2 问题重述
2.模型假设
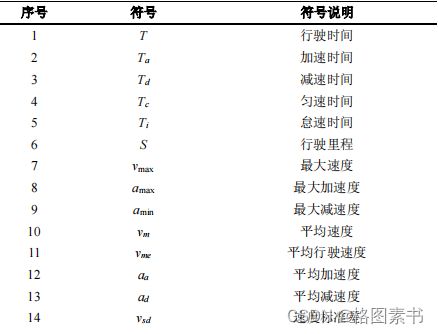
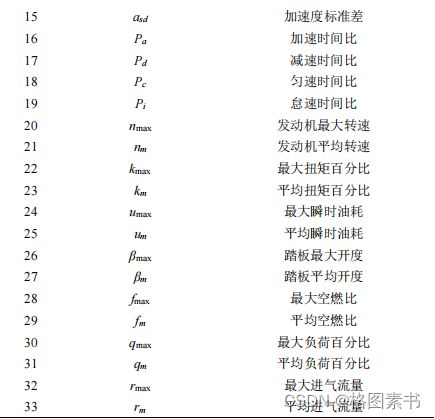
3.符号说明
4.问题一的求解
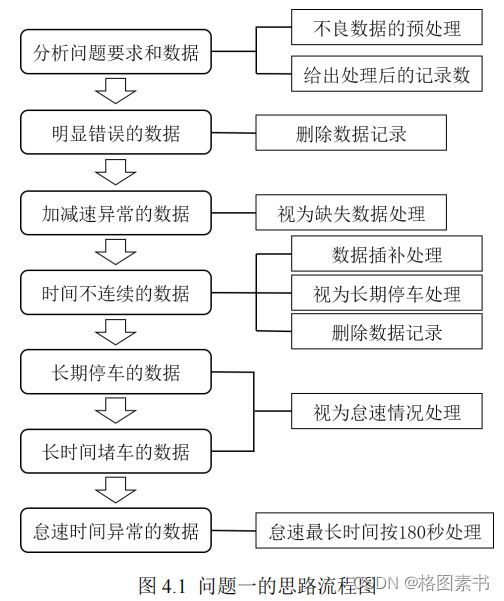
4.1 问题分析
4.2 异常数据的处理
4.2.1 明显错误数据的处理
4.2.2 加减速异常数据的处理
4.3 缺失数据的处理
4.3.1 数据插补处理
4.3.2 视为长期停车处理
4.3.3 删除记录处理
4.4 其他不良数据的处理
4.5 数据预处理结果
5.问题二的求解
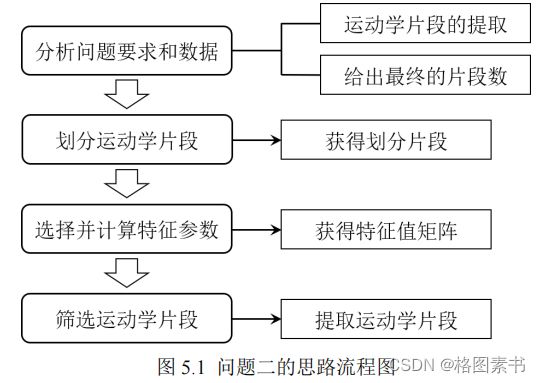
5.1 问题分析
5.2 运动学片段的划分
5.3 特征参数的选择与计算
5.4 运动学片段取
6.问题三的求解
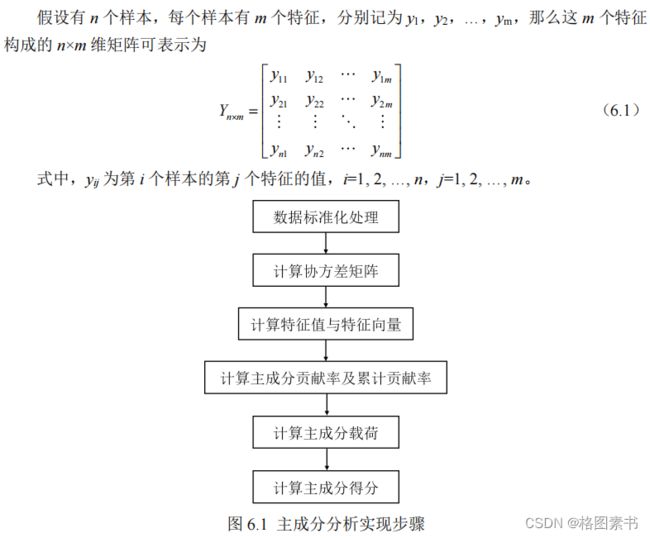
6.1 问题分析
6.2 主成分分析
6.2.1 PCA 基本原理
6.2.2 PCA 编码实现
6.3 K-means 聚类分析
6.3.1 聚类原理
6.3.2 聚类结果与分析
6.4 行驶工况构建
6.4.1 各类运动学片时间占比计算
6.4.2 各类运动学片段选取
6.5 汽车运动特征评估
6.5.1 基于运动学片段特征参数的误差分析
6.5.2 基于油耗特征的行驶工况评价
7.模型的评价与改进
7.1 模型的优点
7.2 模型的缺点
参考文献
代码实现
问题一数据预处理 Python 代码
问题二运动学片段提取 Python 代码
问题三行驶工况构建 Python 代码
摘 要：
汽车行驶工况是一条描述汽车行驶的速度 - 时间曲线，体现了汽车道路行驶的运动学特
征，是汽车行业的一项重要的、共性的基础技术，是车辆能耗 / 排放测试方法和限值标准的
基础，也是汽车各项性能指标标定优化时的主要基准。近年来，随着汽车保有量的快速增
长，我国道路交通状况发生了很大的变化，基于欧洲的 NEDC 行驶工况的标准已不符合我
国目前实际的交通情况。作为车辆开发、评价最为基础的依据，开展深入研究，制定反映
我国实际道路行驶状况的测试工况，具有极其重要的价值。
预处理不良数据（问题一） 根据问题要求，首先采用 SPSS 软件对数据文件进行初步
分析，剔除部分存在明显错误的数据（包括 GPS 车速异常和经纬度异常），以消除因少数
奇异数据带来的整个数据文件有效性降低的影响；对加减速度异常数据视为缺失值处理；
进一步对时间不连续的数据通过设置间隔时间阈值，分别进行数据插补、视为长期停车和
删除数据记录处理，其中数据插补时提出采用一种结合线性插值的拉格朗日插值法；最后
将长期停车和长时间堵车视为怠速状态，并与怠速时间异常数据统一进行处理。在尽量保
留有用信息和减少引入人为数据处理误差的前提下，本文根据上述方法将不良数据进行预
处理，最终各文件数据经处理后的记录数分别为： 178056 组、 140713 组以及 154417 组 。
提取运动学片段（问题二） 根据问题要求，首先利用 Python 语言对经预处理后的数据
进行运动学片段的划分 ， 三个数据文件被划分成的运动学片段数分别为 802 条、 616 条和
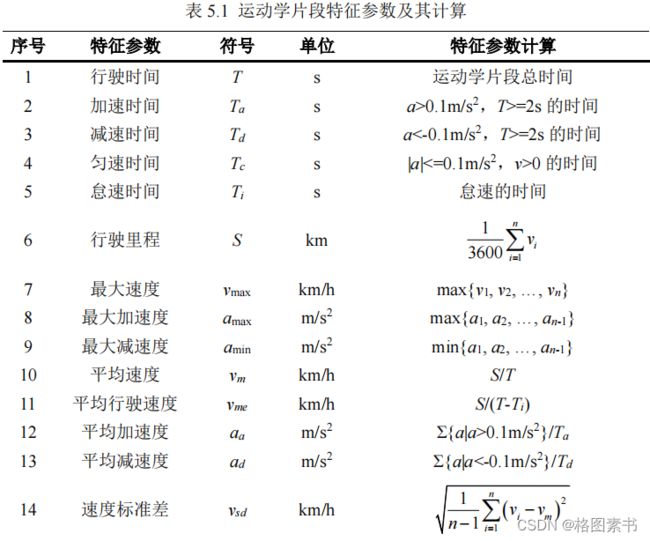
535 条；为保证片段行驶特征描述的全面性，选取并计算了 33 个特征参数 （包括时间，路
程，油耗，（加）速度的最值、均值、标准差和时间占比等），利用求得的特征值矩阵为
后续代表性片段的选取提供了一定的选取标准与评价依据；最后以分析划分的片段长度分
布为基础，结合我国普通轻型汽车的实际特征，并参考 WLTP 提出了运动学片段筛选的三
条准则，最终各文件提取出的运动学片段数分别为： 792 条、 553 条以及 510 条 。
构建并验证工况曲线（问题三） 根据问题要求，首先以主成分分析法对运动学片段特
征参数进行降维处理，最终将 33 维的特征参数数据降为 7 维 ，减小了后续特征聚类的运
算量；基于 Python 语言和聚类方法，对主成分得分矩阵的前 7 列数据采用 K-means 聚类分
对于汽车的采集数据，缺失数据会导致片段划分发生错误，导致一个片段划分成多个
考虑到发动机转速、油耗、转矩等也与汽车的运动状态存在联系，本文确定了 33 个
基于上述分析，为了提高用于构建行驶工况的运动学片段的有效性和合理性，本文确
分析数据文件信息，计算得到的特征参数矩阵数据量过大，较多的变量会带来分析问
调研相关文献[12]， PCA 的基本实现步骤如上图所示，最终保留多少个主成分取决于保
分析表中信息，前 7 个主成分的累计贡献率达到 85.636% ，几乎包含了 33 个定义的特
通过主成分分析，可以得到主成分得分矩阵。由于前 7 个主成分很好地代表了运动学
针对其余四个主成分对聚类结果有贡献程度，方差分析检验结果越显著的变量，对聚
汽车的真实耗油量可由也可由类似的方法计算出。
行驶工况的平均油耗与真是油耗之间的误差约为 3.3%，说明本文构建的行程工况能较
析法进行分类，得到 4 类 运动学片段的行驶工况；最后采用片段组合的方式构建了一条时
长 1221 秒 的汽车行驶工况曲线，并且基于运动学片段特征参数进行了误差分析，相对误
差均 小于 8% ，同时基于油耗特征对行驶工况进行了评价，验证了本文所构建的汽车行驶
工况的合理性。
关键字： 汽车行驶工况；数据预处理；运动学片段；主成分分析； K-means 聚类分析；特
征参数精度评估；油耗评估
1.问题背景与问题重述
1.1 问题背景
汽车行驶工况又称车辆测试循环，是描述汽车行驶的速度与时间的曲线，体现汽车道
路行驶的运动学特征，是汽车行业的一项重要的、共性基础技术，是车辆能耗 / 排放测试方
法和限值标准的基础，也是汽车各项性能指标标定优化时的主要基准。目前，欧、美、日
等汽车发达国家，均采用适应于各自的汽车行驶工况标准进行车辆性能标定优化和能耗 /
排放认证。
本世纪初，我国直接采用欧洲的 NEDC 行驶工况对汽车产品能耗 / 排放的认证，有效
促进了汽车节能减排和技术的发展。近年来，随着汽车保有量的快速增长，我国道路交通
状况发生很大变化，政府、企业和民众日渐发现以 NEDC 工况为基准所优化标定的汽车，
实际油耗与法规认证结果偏差越来越大，影响了政府的公信力。另外，欧洲在多年的实践
中也发现 NEDC 工况的诸多不足，转而采用世界轻型车测试循环（ WLTC ）。但该工况怠
速时间比和平均速度这两个最主要的工况特征，与我国实际汽车行驶工况的差异更大。作
为车辆开发、评价的最为基础的依据，开展深入研究，制定反映我国实际道路行驶状况的
测试工况，显得越来越重要。
另一方面，我国地域辽广，各个城市的发展程度、气候条件及交通状况的不同，使得
各个城市的汽车行驶工况特征存在明显的不同。因此，基于城市自身的汽车行驶数据进行
城市汽车行驶工况的构建研究也越来越迫切，希望所构建的汽车行驶工况与该市汽车的行
驶情况尽量吻合，理想情况下是完全代表该市汽车的行驶情况（也可以理解为对实际行驶
情况的浓缩），目前北京、上海、合肥等都已经构建了各城市的汽车行驶工况。
1.2 问题重述
基于上述研究背景，题目给出了三个数据文件，本文需研究解决以下问题；
问题 1 ：数据预处理
由汽车行驶数据的采集设备直接记录的原始采集数据往往会包含一些不良数据值，不
良数据主要包括几个类型：（ 1 ）时间不连续的数据；（ 2 ）加、减速度异常的数据；（ 3 ）
长期停车所采集的异常数据；（ 4 ）长时间堵车、断断续续低速行驶的数据；（ 5 ）怠速时
间超过 180 秒的异常数据。请设计合理的方法将上述不良数据进行预处理，并给出各文件
数据经处理后的记录数。
问题 2 ：运动学片段的提取
运动学片段是指汽车从怠速状态开始至下一个怠速状态开始之间的车速区间，基于运
动学片段构建汽车行驶工况曲线是目前最常用的方法之一。请设计合理的方法，将上述经
处理后的数据划分为多个运动学片段，并给出各数据文件最终得到的运动学片段数量。
问题 3 ：汽车行驶工况的构建
请根据上述经处理后的数据，构建一条能体现参与数据采集汽车行驶特征的汽车行驶
工况曲线（ 1200-1300 秒），该曲线的汽车运动特征能代表所采集数据源（经处理后的数
据）的相应特征，两者间的误差越小，说明所构建的汽车行驶工况的代表性越好。要求：
（ 1 ）科学、有效的构建方法；（ 2 ）合理的汽车运动特征评估体系；（ 3 ）按照所构建的
汽车行驶工况及汽车运动特征评估体系，分别计算出汽车行驶工况与该城市所采集数据源
（经处理后的数据）的各指标（运动特征）值，并说明所构建的汽车行驶工况的合理性。
2.模型假设
考虑到现实情况，本文做出如下假设：
（ 1 ）假设三个数据文件是某城市的同一辆或同一类汽车采集的；
（ 2 ）假设附件提供的数据绝大部分是真实可靠的；
（ 3 ）假设数据中个别缺失数据对结果不会产生重大影响。
3.符号说明
4.问题一的求解
4.1 问题分析
根据题目要求，采集到的原始数据无法直接拿来使用，低质量的数据将会导致低质量
的挖掘结果。附件提供的数据文件是同一辆车在不同时间段内所采集的数据，由汽车行驶
数据的采集设备直接记录的原始采集数据包含时间、 GPS 车速、加速度、经纬度、发动机
转速、扭矩、油耗等特征。原始数据可能在采集过程中或传输过程中因为传输信号、解码
错误等各种原因出现数据缺失、数据异常等问题，导致数据质量下降，如果直接使用这些
不良数据值得出的结果也会出现偏差。
在本题中，利用 SPSS 软件对三个数据文件进行研究后发现，部分时间段内存在明显
错误的数据，处理不当可能会给最终工况构建及评估体系带来较大误差。比如 “ 某一段时间
内 GPS 车速不等于 0 ，但经度和纬度却始终保持不变 ” ，其产生的原因可能是 GPS 或采集
传感器设备异常。这种明显违反常识的错误数据，应当予以剔除。
因此在调研相关文献 [1-5]，了解数据挖掘的一些常用方法后，本文确定先对存在明显错
误的数据进行删除处理，然后对加减速异常的数据视为缺失数据处理，再然后对时间不连
续的数据分别进行数据插补、视为长期停车和删除数据记录处理，最后对长期停车、长时
间堵车和怠速时间异常的数据统一进行处理。确定的问题一总体思路如下图所示。 
这里我们将存在明显错误的数据、加减速异常的数据都视为异常数据处理；时间不连
续的数据视为缺失数据处理；长期停车的数据、长时间堵车的数据、怠速时间异常的数据
都视为怠速数据处理。
4.2 异常数据的处理
为方便对数据进行预处理以及后面进一步的计算，文本将数据记录中的时间转换成了
数值型。考虑到给出的三个原始数据文件中数据记录的最早时间为 2017 年 11 月 1 日傍晚，
因此，本文将所有的记录时间转换为距离 2017 年 11 月 01 日 00 时 00 分 00 秒的秒数。
原始的采集数据会出现一些异常值。异常值是与其他观测值或预期数值有明显差别的
值。查阅相关文献 [6,7] ，在数据处理中，异常值的处理方法通常有：删除记录、视为缺失值、
平均值修正和不处理。异常值是否剔除，需要视具体情况分析而定。分析异常值出现原因，
将有助于我们判断异常值是否舍弃。
4.2.1 明显错误数据的处理
附件提供的数据文件是某城市轻型汽车实际道路行驶采集的数据（采样频率 1Hz ），
每个数据文件反应的是同一辆车在不同时间段内所采集的数据。但是由于采集设备的精度
和稳定性不够等各种因素，有时会出现明显不符合常理的错误数据。为了后续数据的处理，
需要对这些明显错误的数据进行简单处理。
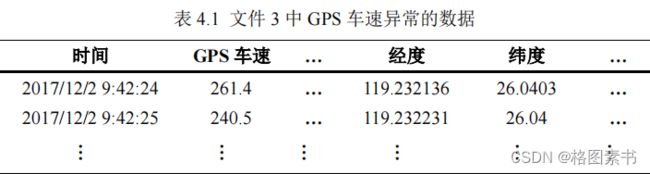
（ 1 ） GPS 车速异常
文件 3 中 GPS 车速最大值为 261.4km/h ，且车速大于 120km/h 的有近 300 条。根据《中
华人民共和国道路交通安全法实施条例》，在高速公路上行驶的小型载客汽车最高车速不
得超过每小时 120 公里。文件中所提供的是某城市轻型汽车实际道路行驶采集的数据，结
合交通道路状况和车辆自身特性确定车辆的最高行驶车速 v max =120km/h ，因此本文中将
GPS 车速大于 120km/h 的数据视为异常数据，应当予以剔除。 
（ 2 ）经度和纬度数据异常
调研相关文献 [8,9] 可知， GPS 确定与计算速度的原理是： GPS 接收器可以利用其输出
TTL 数椐算出每一秒钟的具体经纬度坐标，然后再除以一秒钟，就是一秒钟内的平均速度。
经纬度是根据卫星定位，然后通过网点坐标信息来确定的。实际应用中，由于各种误差，
导致这样算出来的数据不可能那么准确。
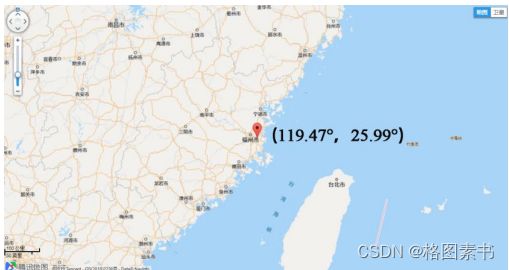
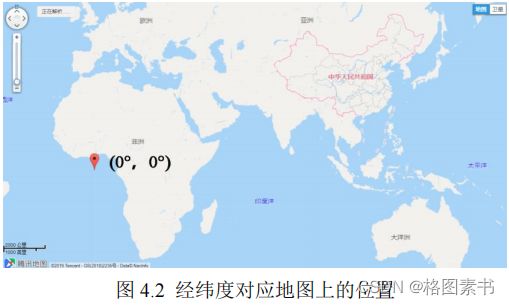
借助腾讯地图软件，经度和纬度都是 0° 的地方位于 0° 经线和赤道的交汇处的几内亚湾
里，位于东半球，而题目中的汽车行驶范围大致在 119.47°E ， 25.99°N 的中国福州市内，
正常行驶显然不可能出现经度和纬度都是 0° 的情况。这些异常数据可能是由于 GPS 仪器
故障产生，应当予以剔除。 
上述的异常数据在文件 1 中有 3 组，如下表所示，文件 2 中有 300 组，文件 3 中没有。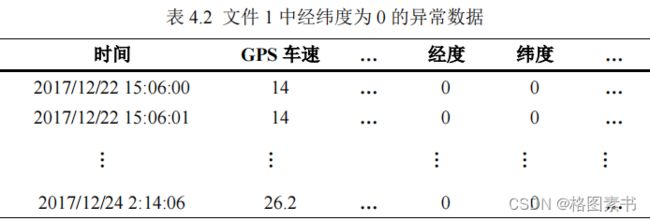
此外，由 GPS 测速原理可知，在一段连续的时间内 GPS 车速不等于 0 ，说明汽车在持
续行驶，经度和纬度应随着时间的推移产生相应的数值变化，而不可能始终保持不变，这
显然不合常理。本文中将这些车速与经纬度不一致的数据视为异常数据，应当予以剔除。 
4.2.2 加减速异常数据的处理
数据文件中的 X 轴加速度、 Y 轴加速度、 Z 轴加速度分别为采集设备上传感器采集到
的加速度，其中，坐标系以汽车质心为原点，行驶方向为 X 轴 , 横向方向 Y 轴，地面垂直
方向为 Z 轴。本文中主要以 GPS 车速来衡量汽车的运行速度，至于 X 、 Y 、 Z 轴加速度与
汽车运行速度没有直接的联系。为处理加减速异常的数据，需要求出各个时间点 GPS 车速
所对应的加速度值，其计算公式为： 
速度的跳变是汽车车速采集中最常出现的异常数据，速度的突变会导致汽车在某一或
某些时刻加 / 减速度过大，这显然是不合常理的。汽车加速度异常的影响因素复杂，本文中
不做过多分析。一般情况下，汽车在城市间行驶时不会有急加速和急减速（事故急刹车除
外），加 / 减速度过大不具有代表性，且多为设备采集问题，而且会对结果造成较大的偏差，
因此需要对加速度异常值进行处理。
（ 1 ）加速度异常
百公里加速指的是 0 到 100km/h 的加速时间，是对汽车动力最直观的体现。不同的环
境温度、路面状况以及车辆损耗状况甚至油箱剩余燃油的多少都会对百公里加速时间造成
影响。一般紧凑型轿车百公里加速成绩在 11~13 秒之间，中型轿车在 7~8 秒之间，而超级
跑车的加速时间大都小于 3.8 秒。本文中，确定普通轿车一般情况下的百公里加速时间大
于 7 秒，小于或等于 7 秒的数据视为加速异常数据。按照平均加速度计算，加速度大于 4 m/s 2
的数据视为加速度异常，剔除数据并视为缺失值处理。
（ 2 ）减速度异常
最大减速度与车辆刹车性能有关，也与道路路面摩擦系数有关。从汽车应具有的制动
能力来说，紧急制动时，汽车的最大减速度一般为 7.5~8 m/s 2 ；普通制动时，汽车的平均
减速度应为 3~4 m/s 2 。但在实际使用制动时，除紧急情况外，通常不应使制动减速度大于
1.5~2.5 m/s 2 ，否则不仅会使乘客感到不舒服或发生危险或造成货物不安全，而且还会增加
油耗，加剧轮胎的磨损。本文中，确定普通轿车一般情况下的紧急刹车最大减速度在 7.5~8
m/s 2 ，超过 8 m/s 2 的减速度视为减速异常数据。将上述异常数据中的速度值视为缺失值，
并在下文中于不连续时间数据一起进行数据插值处理。其他异常值暂不处理，因为在数据
预处理时，有些异常值可能蕴含一些有用信息，因此保留其他不确定的异常值。
4.3 缺失数据的处理
在汽车数据采集的过程中，可能会出现数据缺失的现象。造成这种现象的原因可能是
仪器数据线的连接不紧，或者是短时间内速度传感器未能感应速度的瞬间变化，也可能是
由于设备通信、车辆震动等导致有些数据没能成功上传。统计学将数据缺失的记录称为不
完全观测，这种数据缺失或不完全观测对调查研究有着很大的影响。对于缺失数据，从缺
失的分布来讲可以分为完全随机缺失（ MCAR ）、随机缺失（ MAR ）和完全非随机缺失
（ MAR ）。而对于时间序列类的数据，可能存在随着时间的缺失，这种缺失称为单调缺失。
经分析并根据上述描述可知，加减速异常数据中视为缺失值的速度值，属于随机缺失；
题目所给出的数据文件中由于高层建筑覆盖或过隧道等导致 GPS 信号丢失的时间不连续
情况，该数据属于单调缺失。调研相关文献 [10] ，处理缺失值的方法通常有三类：删除记录、
数据插补和不处理。数据插补只是将未知值补以我们的主观估计值，也会带来一定的误差。
常用的插补方法有均值插补、利用同类均值插补、极大似然估计以及多重插补。
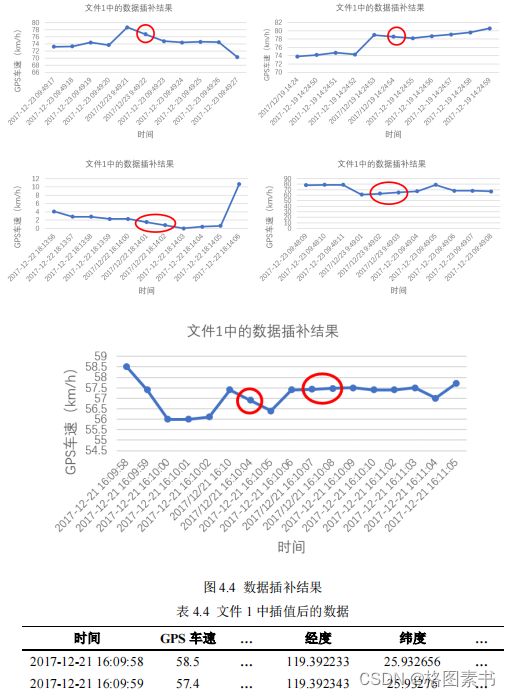
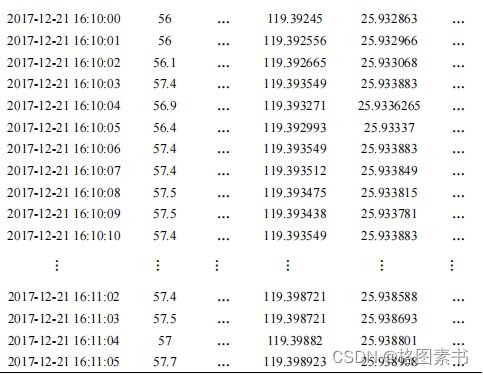
本文中确定将经处理后的数据中时间间隔小于或等于 3s 的不连续数据，采用插补法中
的拉格朗日插值法结合均值插值法进行插补处理。对于时间间隔大于 3s 的不连续数据，如
果（ 1 ）间隔两端 GPS 速度均为 0 ，且定位距离小于 10m ，则将缺失时间内汽车的运动状
态视为长期停车状态；（ 2 ）间隔两端 GPS 速度不都为 0 ，且缺失时间过长无法修正，则
删除间隔两端到相邻怠速状态间的记录。
4.3.1 数据插补处理
拉格朗日插值（ Lagrange interpolation ）是一种多项式插值方法，拉格朗日插值法可以
给出一个恰好穿过二维平面上若干个已知点的多项式函数。其数学原理为：对某个多项式
函数有已知的 n +1 个点，假设任意两个点互不相同，那么应用拉格朗日插值公式所得到的
拉格朗日插值多项式为： 
对于时间间隔小于或等于 3s 的不连续数据，每个间隔需要插值的点数较少（小于等于
2 个）。在插值计算中，为了减少截断误差，选择插值节点时应尽量选取与插值点距离较
近的一些节点。由于源数据本身存在很多时刻数据的缺失，再加上对异常数据剔除后，使
得缺失的时刻更多，本文中对连续缺失小于等于 3 秒的数据进行插值，取缺失部分的前后
5 个点的数据对缺失部分进行拉格朗日插值。由于存在多个缺失部分可能靠得很近的情况，
导致无法在相邻时刻（本文采取缺失部分前后 10 秒的范围）内找到足够的点，因此，本
文采用线性插值进行替代，部分插补结果和数据如下： 
4.3.2 视为长期停车处理
对于时间间隔大于 3s 的不连续数据，如果间隔两端 GPS 速度为 0 则视为长期停车处
理，其工况状态视为怠速状态。
4.3.3 删除记录处理
对于时间间隔大于 3 秒的不连续数据，如果间隔两端的 GPS 速度不全为 0 ，无法确定
两端行驶情况，则需要对数据进行进一步丢弃。若左端为 0 而右端不为 0 ，对右端数据进
行删除，直到右端数据为 0 ；若左端不为 0 而右端为 0 ，对左端数据进行删除，直到左端
数据为 0 ；若两端数据都不为 0 ，对两端数据进行删除，直到两端数据为 0 。
4.4 其他不良数据的处理
怠速是指发动机在无负荷的情况下运转，只需克服自身内部机件的摩擦阻力，不对外
输出功率。维持发动机稳定运转的最低转速被称为怠速。结合上述怠速定义，对于长期停
车的情况（如停车不熄火等候人、停车熄火了但采集设备仍在运行等）以及长时间堵车、
断断续续低速行驶的情况（最高车速小于 10km/h ），本文中全部视为汽车处于怠速状态。
长时间原地怠速很容易导致汽车油封和密封垫漏油，同时容易产生大量的积碳。怠速
时间过长的短行程没有表现交通特征，且对结果也会产生较大偏差。因此本文中将怠速时
间超过 180 秒为异常情况，怠速最长时间可按 180 秒处理。
4.5 数据预处理结果
根据上述方法将不良数据进行预处理，各文件数据经处理后的结果 
5.问题二的求解
5.1 问题分析
根据题目要求，基于运动学片段构建汽车行驶工况曲线是目前最常用的方法之一，将
采集到的数据按照某种原则划分成许多片段进行分析，这种方法使得分析更加方便、精度
更高。汽车在同一路段在不同的时间、天气和交通等状况下会表现出不同的行驶特征。例
如，高速公路会出现堵塞特征，而市区拥挤的道路也可能会出现畅通特征，只是所占的比
例大小不同。因此，将提取的运动学片段和行驶特征联系在一起，在此基础上构建汽车行
驶工况是完全合理的。
对于汽车的采集数据，缺失数据会导致片段划分发生错误，导致一个片段划分成多个
片段或者最终无法形成一个完整的运动学片段，从而丢失大量有用的数据信息。分析数据
文件信息，在问题一的数据预处理过程中，缺失数据都分别得到相应的处理，确保了运动
学片段划分的有效性和合理性。
调研相关文献 [11] ，本文确定先按照 GPS 车速数据特征将处理后的数据划分成多个运动
学片段，然后计算并分析运动学片段的特征参数，最后依据一定的筛选规则进行运动学片
段的提取。确定的问题二总体思路如下图所示。
5.2 运动学片段的划分
汽车从起步出发到行驶至目的地停车，由于道路环境、交通管制、其他车辆的影响等，
在行驶过程中会有频繁的起步、加速、减速、停车等操作，由多个 “ 停 - 走 - 停 ” 的过程组成。
运动学片段是指汽车从怠速状态开始至下一个怠速状态开始之间的车速区间，通常包含一
个怠速部分和一个行驶部分，而行驶部分通常包括加速、匀速和减速三种行驶模式。
根据题目中的名词解释，将汽车行驶工况分为加速工况、匀速工况、减速工况和怠速
工况四种，他们的定义如下：
（ 1 ）加速工况：汽车加速度大于 0.1m/s 2 且速度不等于 0 的行驶状态；
（ 2 ）匀速工况：汽车加速度的绝对值小于 0.1m/s 2 且速度不等于 0 的行驶状态；
（ 3 ）减速工况：汽车加速度小于 0.1m/s 2 且速度不等于 0 的行驶状态；
（ 4 ）怠速工况：汽车发动机运转，但车速等于 0 的行驶状态。
三个文件经数据预处理后分别有 178056 组、 140713 组、 154417 组数据，数据量庞大，
因此本文采用 Python 程序进行运动学片段划分，最终三个数据文件被划分成的运动学片段
数分别为 802 、 616 和 535 。
5.3 特征参数的选择与计算
由于道路交通状况的影响，运动学片段之间也存在较大的差异。不同的运动学片段反
映了汽车在实际运行过程中的不同的行驶状况和交通特征。将原始数据按照一定原则分割
成运动学片段，这样处理后的数据就是由许多数据单元组成。
根据上述分析，汽车实际行驶工况是由多个具有一定代表性的运动学片段组成的，代
表性行驶工况就是从大量的运动学片段中选择一定数量合适的片段组合而成的，在选择的
过程中需要一定的选取标准与评价依据。划分的运动学片段中只有 GPS 速度和时间数据，
但是仅仅采用速度和时间数据并不能够很好地描述各个运动学片段。在评价代表性行驶工
况时，可以使用特征参数来评估该工况，国内外一般采用平均（加）速度、最大（加）速
度、（加）速度分布等参数来代替速度和时间作为运动学片段的特征参数，以达到统计维
数上的一致。但是如果特征参数过多，既增加了计算工作量，也给分析和解释问题带来了
不必要的困难。分析数据文件信息， X 轴、 Y 轴、 Z 轴的最大和平均加速度值均在 -1~1 之
间浮动变化，如下图所示，因此本文中不考虑将三轴加速度作为特征参数。
考虑到发动机转速、油耗、转矩等也与汽车的运动状态存在联系，本文确定了 33 个
特征参数来描述所有的运动学片段，保证了片段描述的全面性，各特征参数详细含义如下
表所示。
利用采集到的 GPS 速度和时间数据来计算特征参数的过程，可以看作是数据分析中的
数据变换，特征参数能够从多个角度描述一个运动学片段的交通特征，更利于数据分析。
运动学片段的特征参数可以分为时间，路程，油耗，（加）速度的最值、均值、标准差和
时间占比等。速度和时间采集的频率为 1 Hz ，运动学片段特征参数的计算公式如上表所示。
利用上述计算公式，将所有运动学片段计算出的特征参数值组合在一起，就可以得到
一个以各个运动学片段为样本，样本数量 ( 行 )× 特征参数 ( 列 ) 的矩阵，如下表所示。该矩阵
可用于行驶工况构建过程中。
5.4 运动学片段取
对划分后的运动学片段数据进行分析，得到片段长度分布比例如下图所示。由于长度
在 0~10s 和大于 500s 的运动学片段所占比例不足 6% ，所以认为其包含有用信息的可能性
较小，应当予以剔除。
基于上述分析，为了提高用于构建行驶工况的运动学片段的有效性和合理性，本文确
定以国家法规为基础，结合我国普通轻型汽车的实际特征，并参考全球统一轻型车辆测试
程序（ Worldwide Harmonised Light Vehicle Test Procedure, WLTP ），该测试分为低速、中
速、高速与超高速四部分，其对应的持续时间为 589s 、 433s 、 455s 、 323s ，且对应的最高
速度分别为 56.5km/h 、 76.6km/h 、 97.4km/h 、 131.3km/h 。据此，提出运动学片段筛选的三
条准则：
（ 1 ）运动学片段持续时间低于 10s ；
（ 2 ）运动学片段持续时间超过 500s ；
（ 3 ）加速度绝对值大于 4 m/s 2 的运动学片段。
基于上述筛选准则，三个数据文件经筛选后提取的运动学片段数分别为 792 、 553 、 510 ，
相较于划分的运动学片段数分别减少了 1.25% 、 10.23% 、 4.67% ，如下表所示。
6.问题三的求解
6.1 问题分析
根据题目要求，汽车行驶工况曲线的构建是在原始数据预处理以及运动学片段提取完
成的基础上，运用各种理论模型或数学方法进行数据分析，然后通过聚类分析将代表不同
行驶特征的运动学片段分类再抽取，组成代表性工况，最终拟合出一条能体现参与数据采
集汽车行驶特征的工况曲线。根据上述分析，聚类效果的好坏对最终拟合出的行驶工况的
精度起着决定性的作用。
分析数据文件信息，计算得到的特征参数矩阵数据量过大，较多的变量会带来分析问
题的复杂性，导致在对运动学片段进行聚类分析时会出现计算效率低、不宜聚类等各种问
题。通常而言，虽然每个特征参数都提供了一定的信息，但是其重要性不同，而且各个特
征参数之间经常具有一定的相关性，例如行驶时间、行驶里程和平均速度这几个特征参数
是高度相关的，使得它们提供的信息产生重叠。采用降维处理方法，把高维的数据转变为
低维数据，可以有效解决冗余特征带来的多重共线性问题。
本文确定先采用主成分分析法进行降维处理以减少特征参数的数目，减小下一步的特
征聚类运算量，同时为主成分的计算提供定量表达式。确定的问题三总体思路如上图所示。
6.2 主成分分析
主成分分析（ Principal components analysis ，以下简称 PCA ）是一种通过降维技术把多
个变量化为少数几个主成分的统计方法，是基于降维思想下产生的处理高维数据的方法。
它可以对高维数据进行降维以减少预测变量的个数，同时经过降维除去噪声。
主成分分析的主要目的是希望用较少的特征去解释原来数据中的大部分变异，将我们
手中许多相关性很高的特征转化成彼此相互独立或不相关的特征。通常是选出比原始特征
个数少，能解释大部分数据中的变异的几个新特征，即所谓主成分，并用以解释数据的综
合性指标。
6.2.1 PCA 基本原理
调研相关文献[12]， PCA 的基本实现步骤如上图所示，最终保留多少个主成分取决于保
留部分的累计贡献率。为了保证不到丢失掉主要信息，本文确定保留的主成分累计贡献率
应当大于 80% 。
6.2.2 PCA 编码实现
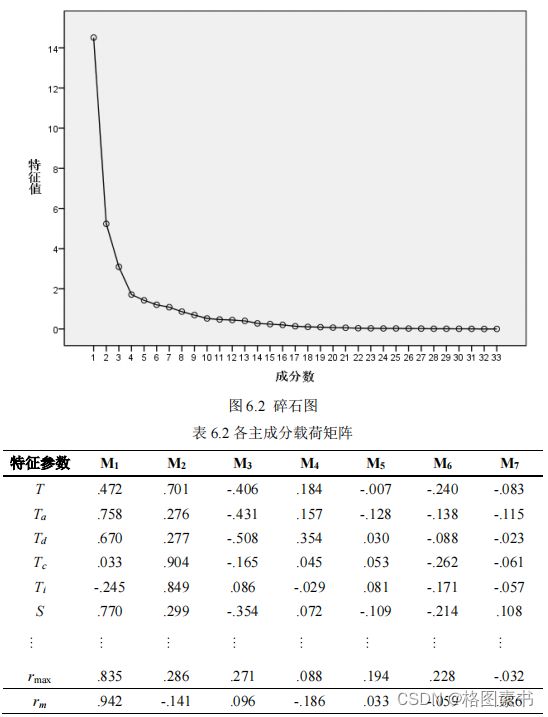
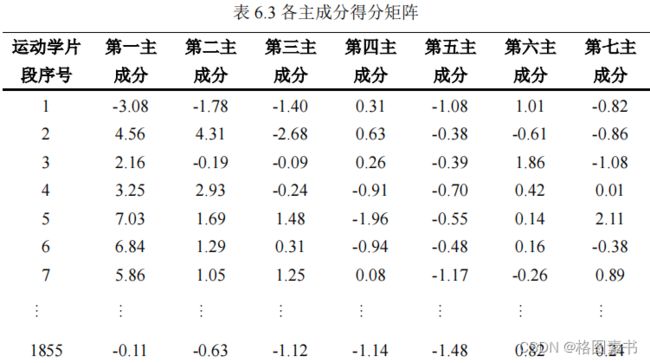
采用 SPSS 软件对三个数据文件中的运动学片段进行主成分分析，最终将 33 维的特征
参数数据降为 7 维。用主成分的得分代替特征参数来描述原运动学片段的行驶特性，各主
成分的贡献率、累计贡献率如下表所示。
分析表中信息，前 7 个主成分的累计贡献率达到 85.636% ，几乎包含了 33 个定义的特
征参数的绝大部分信息。根据表中特征值做出碎石图，如下图所示，每一个特征称为 1 个
因子，总共有 33 个特征，即 33 个因子。第七主成分方差为 1.082>1 ，第八主成分方差为
0.862 。因此，前 7 个主成分很好地代表了整个运动学片段的行驶特性。
在主成分载荷矩阵中，如下表所示，给出了主成分的载荷系数。每一列载荷值都是各
个参数与有关主成分的相关系数。某个参数在某个主成分上的载荷系数的绝对值越大，就
说明这个参数与这个主成分的相关系数就越高。分析表格信息可知，（ 1 ）主成分 M 1 主要
反映了特征参数平均进气流量；（ 2 ）主成分 M 2 主要表达的信息为匀速时间；（ 3 ）主成
分 M 3 主要反映了平均减速度；（ 4 ）主成分 M 4 主要反映了最大加速度；（ 5 ）主成分 M 5
和 M 6 主要表达的信息为最大瞬时油耗；（ 6 ）主成分 M 7 主要反映了平均空燃比。
通过主成分分析，可以得到主成分得分矩阵。由于前 7 个主成分很好地代表了运动学
片段的特征参数，因此本文中聚类分析的样本取主成分得分矩阵的前 7 列进行分析，如下
表所示。
6.3 K-means 聚类分析
同一个路段含有不同的交通特征，但运动学片段之间可能含有相同的交通特征。为了
符合我国混合交通的特点，需要对不同的短行程按照道路交通特征分类，将拥有相同交通
特征的运动学片段分为一类，并将不同类别的片段组合成代表性行驶工况。因此，需要构
造聚类模型，根据行驶状况（使用特征参数表征）将不同的运动学片段进行分类。
6.3.1 聚类原理
聚类分析方法在大数据的挖掘处理过程中起着重要的作用，目前聚类方法主要有划分
聚类、层次聚类、基于密度的聚类、基于网格的聚类和基于模型的聚类等，其中应用较为
普遍的是 K-means 聚类。 K-means 算法中的 K 代表类簇个数， means 代表类簇内数据对象
的均值（这种均值是一种对类簇中心的描述），因此， K-means 算法又称为 K- 均值算法。
K-means 算法是一种基于划分的聚类算法，以距离作为数据对象间相似性度量的标准，即
数据对象间的距离越小，则它们的相似性越高，则它们越有可能在同一个类簇。数据对象
间距离的计算有很多种， K-means 算法通常采用欧氏距离来计算数据对象间的距离。算法
优缺点如下表所示。
（ 3 ）重新计算每个簇中对象的平均值，用此平均值作为新的聚类中心；
（ 4 ）重复上述步骤，直到类簇中心不再发生变化。
6.3.2 聚类结果与分析
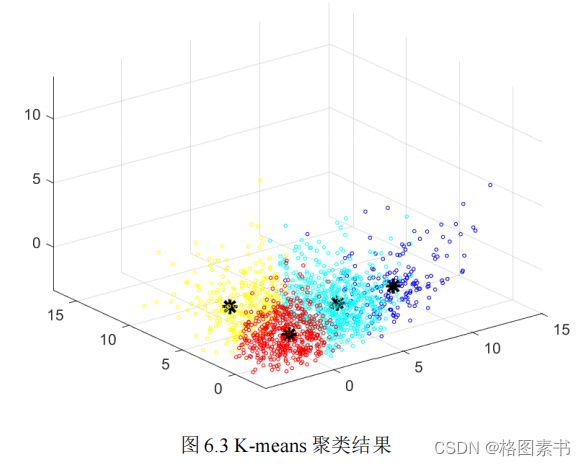
本文采用 SPSS 软件对前 7 列主成分进行运动学片段的聚类分析，设置聚类数为 6 ，迭
代次数为 50 次。经过 16 次迭代，聚类中心收敛。为了形象表述聚类效果，选取七个主成
分中的前三个，将其标准化后，聚类结果如下图所示。由图可知， 1855 个运动学片段被分
成了 4 类。其中第一类（黄色点表示）共有 615 个片段，第二类（红色点表示）共有 406
个片段，第三类（蓝色点表示）共有 190 个片段，第四类（浅蓝色点表示）共有 644 个片
段。图中黑色 “*” 号分别为 4 个聚类中心，由图可见各中心的间距基本相同，分类较均匀。
针对其余四个主成分对聚类结果有贡献程度，方差分析检验结果越显著的变量，对聚
类结果越有影响。如表 6.5 ，七个主成分在 F 检验下， α 值均小于 0.01 ，表明所选主成分明
显影响聚类结果。
6.4 行驶工况构建
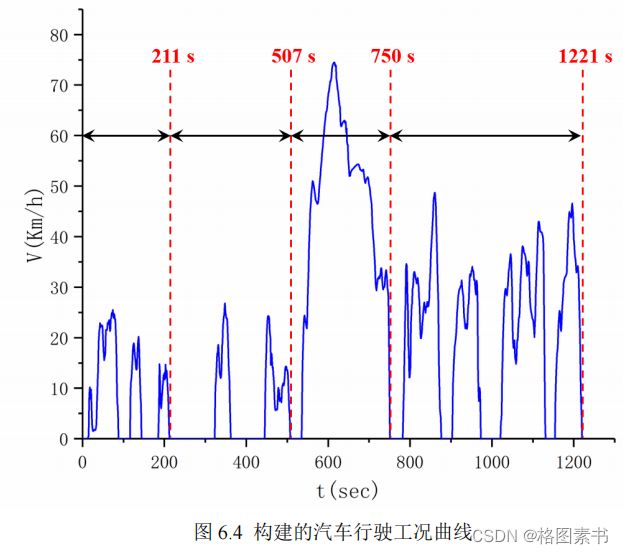
在用片段组合的方式构建典型工况之前，首先要确定需要合成的典型工况的持续时
间。根据题目要求，本文选取 1200s ～ 1300s 作为标准。
6.4.1 各类运动学片时间占比计算
提取的 1855 个运动学片段的总时间为 231740 秒，四类运动学片段的总时间分别为
41193 秒， 57387 秒， 46019 秒和 87141 秒。按四类运动学片段的时间总和的占比分配行驶
工况时间，计算得到第一类运动学片段约占行驶工况时间 213 到 231 秒，第二类运动学片
段越占 291 到 322 秒，第三类运动学片段约占 238 到 258 秒，第四类运动学片段约占 451
到 489 秒。
6.4.2 各类运动学片段选取
计算各类运动学片到所属簇中心的距离，并分别在类内按距离从小到大的顺序排序，
选取靠近簇中心的运动学片段构成典型工况，选取运动学片段的具体步骤如下：
STEP1 ： 类内抽取若干运动学片，使得片段时间的总和接近该类所占行驶工况时间；
STEP2 ： 判断四类运动学片段构成的典型行驶工况时间是否满足要求，若满足，该组
合作为备选行驶工况，若大于 1300 秒，转到 STEP3 ，若小于 1200 秒，转到 STEP4 ；
STEP3 ： 对运动学片段时间总和小于所占行驶工况时间的类，考虑增加运动学片段的
数目获选择更长的运动学片段，再转到 STEP2 进行判断；
STEP4 ： 对运动学片段时间总和大于所占行驶工况时间的类，考虑减少运动学片段的
数目获选择较短的运动学片段，再转到 STEP2 进行判断。
工况构建结果如下图所示，从图中可以看出，该市车辆行驶的平均车速低于 40 km/h ，
30% 的时间都处于怠速状态，说明该市的交通较拥堵。
6.5 汽车运动特征评估
6.5.1 基于运动学片段特征参数的误差分析
在运动学片段的 33 个特征中，选择包括平均速度在内的受片段选取影响较小，更具
普遍意义的 17 个特征对工况曲线进行评价，计算工况曲线对整个行驶状态进行描述上的
误差，误差评价指标的计算公式如下所示：
其中 Value _ total 为在所有运动学片段上计算的特征值， Value _ curve 为在构成行驶工况
曲线的运动学片段上计算的特征值。最终得到的误差分析情况如下图所示。
6.5.2 基于油耗特征的行驶工况评价
道路行驶工况的主要用途之一就是评价汽车燃油的消耗水平，所以工况性能的好坏主
要取决于汽车在行驶状态下的真实油耗水平和工况之间的差异。基于国家标准（如
《 GB27840-2011 重型商用车辆燃料消耗量测量方法》），在实验室里根据汽车行驶工况曲
线，按照一定的标准，经检测、计算得出。由于本文构建的汽车行驶工况是基于短行程片
段依据一定统计规律组合来构建，该工况对应的油耗水平可以参考原始数据中瞬时油耗
（ ml/s ）按照时间时间序列的累加来计算。
汽车的真实耗油量可由也可由类似的方法计算出。
可得，行驶工况描述的汽车耗油量与真实耗油量的相对误差为：
行驶工况的平均油耗与真是油耗之间的误差约为 3.3%，说明本文构建的行程工况能较
好的代表该型汽车在当地的真实行驶状态。
7.模型的评价与改进
7.1 模型的优点
本文针对不同的错误数据、异常数据、缺失数据等，综合运用了 Python 、 SPSS 、 Excel 、
Matlab 等统计分析软件对数据进行处理，在保存大部分有用数据信息的前提下得到了较为
合理的数据处理结果。基于运动学片段构建汽车行驶工况曲线是目前最常用的方法之一，
本文选取并计算了 33 个特征参数，保证了片段行驶特征描述的全面性，使得片段提取的
结果更加贴近实际情况，合理可靠。本文采用了主成分分析法进行降维处理以减少特征参
数的数目，减小下一步的特征聚类运算量，同时有效利用了 K-means 聚类方法适合于大数
据处理、简单高效等特点。最后采用片段组合的方式构建了典型汽车行驶工况曲线，并且
基于运动学片段特征参数进行误差分析，同时基于油耗特征对行驶工况进行评价，计算出
汽车行驶工况与处理后数据的运动特征，验证了本文所构建的汽车行驶工况的合理性。
7.2 模型的缺点
由于数据文件中的特征指标较多，每个文件的初始样本量更是高达十万条，给数据量
化处理工作带来较大困难，因此在筛选过程中会遗漏部分可能存在重要作用的变量信息，
并且我们在预处理的时候，可能方法不尽合理，会对结果造成一定程度的影响。另外，由
于异常数据剔除后，丢弃一些特征会造成部分有用信息的丢失，所以得到的结果可能会存
在一些可接受的误差。最后，本文中对于部分异常特征参数的识别机制认识的不够完善，
比如与汽车运动没有直接联系的特征参数（ X 轴、 Y 轴、 Z 轴加速度）。
参考文献
代码实现
问题一数据预处理 Python 代码
import pandas as pd
import numpy as np
import datetime
import tqdm
def segments(rawData):
seg_bound=0
n=1
maxl=0
maxb=0
count=0
while n180:
seg_bound=n-180
n+=1
elif rawData.iat[n-1,1]==0 or rawData.iat[n,1]!=0:
n+=1
else:
if n-seg_bound>maxl:
maxl=n-seg_bound
maxb=seg_bound
count+=1
n+=1
seg_bound=n
return maxl,maxb
def checkMissing(rawData):
jump=[]
for i in range(1,len(rawData)):
diff =(rawData.iat[i, 0]-rawData.iat[i-1, 0]).total_seconds()
if diff>3:
jump.append(diff)
return jump
def checkSlow(rawData):
seg_bound=0
n=1
maxl=0
maxb=0
count=0
while n180:
seg_bound=n-180
n+=1
elif rawData.iat[n-1,1]==0 or rawData.iat[n,1]!=0:
n+=1
else:
if n-seg_bound>maxl:
maxl=n-seg_bound
maxb=seg_bound
count+=1
n+=1
seg_bound=n
return maxl,maxb
def process(rawData):
print(list(rawData))
i=0
while i100 and rawData.iat[i,0]-rawData.iat[j,0]<=7:
res.append(j)
else:
i+=1
return res
def findMissing(rawData):
res = []
for i in range(1,len(rawData)):
diff =(rawData.iat[i,1]-rawData.iat[i-1,1]).total_seconds()
if 110 and
rawData.iat[i+1,8]==rawData.iat[i,8] and rawData.iat[i+1,9]==rawData.iat[i,9]:
j=i
while (rawData.iat[i+1,1]-rawData.iat[i,1]).total_seconds()==1 and rawData.iat[i,2]>10 and
rawData.iat[i+1,8]==rawData.iat[i,8] and rawData.iat[i+1,9]==rawData.iat[i,9]:
i+=1
res.append([j,i+1-j])
else:
i+=1
for r in res:
print(r[0],r[1])
def removeError(rawData):
print(' ',rawData.shape[0])
i=1
while i10 and rawData.iat[i-1,9]==rawData.iat[i,9] and
rawData.iat[i-1,10]==rawData.iat[i,10]:
rawData.drop(rawData.index[i], inplace=True)
else:
i+=1
print(' ', rawData.shape[0])
i=0
while i4 or rawData.iat[i, 5]<-8:
rawData.drop(rawData.index[i], inplace=True)
else:
i+=1
print(' ', rawData.shape[0])
i = 0
while i120:
rawData.drop(rawData.index[i], inplace=True)
else:
i+=1
print(' ', rawData.shape[0])
# rawData[' ']=rawData[' '].astype('str')
rawData.to_excel('/Users/yangkai/Downloads/questionD/ 3 .xlsx')
def Interpolation(rawData):
col = list(rawData)
print(col)
data= list(np.array(rawData))
print(len(rawData))
i=1
while i=0:
if rawData.iat[i,3]==0:
count+=1
if count>180:
while rawData.iat[i,3]==0:
rawData.drop(rawData.index[i], inplace=True)
i-=1
else:
i-=1
else:
count=0
i-=1
print(len(rawData))
df = pd.read_excel('/Users/yangkai/Downloads/questionD/ 1 .xlsx')
# print(list(df))
# df[' '] = pd.to_datetime(df[' '], format='%Y/%m/%d %H:%M:%S.000.')
# begin = datetime.datetime.strptime('2017-11-01 00:00:00', '%Y-%m-%d %H:%M:%S')
# df['unix '] = df[' '].map(lambda x:(x-begin).total_seconds())
# col=list(df)
# rawData = df[col[1:-3]]
df[' '] = df[' '].astype('str')
# process(df)
# i=0
# while i 120:
# df.drop(df.index[i], inplace=True)
# else:
# i += 1
# df.to_excel('/Users/yangkai/Downloads/questionD/ 3 .xlsx')
#df[' ']=pd.to_datetime(df[' '],format='%Y-%m-%d %H:%M:%S')
# df['DIFF']=df[' '].diff(1).dt.seconds
# df['DIFF'].fillna(0)
# print(df.head(10))
# print(len(df))
# print(list(df))
# i️dleSpeedprocess(df)
# i️dleSpeed(df)
Interpolation(df)
# removeError(df)
# removeAbnormalAcceleration(df) 问题二运动学片段提取 Python 代码
import numpy as np
import pandas as pd
def getTimepiece(df):
print(list(df))
seg=[[0]]
for i in range(len(df)-1):
if df.iat[i,3]!=0 and df.iat[i+1,3]==0:
if df.iat[i+1,1]-df.iat[i,1]==1:
seg[-1].append(i)
else:
seg.pop(-1)
seg.append([i+1])
seg.pop(-1)
i=0
while i500 or seg[i][1]-seg[i][0]<0:
seg.pop(i)
else:
i+=1
for i in range(len(seg)):
count=0
for j in range(seg[i][0],seg[i][1]+1):
if df.iat[j,1]==0:
count+=1
else:
break
if count>180:
seg[i][0]=seg[i][0]+count-180
# print(' :',len(seg))
# temp=[x[1]-x[0]+1 for x in seg]
# temp.sort()
# for t in temp:
# print(t)
return seg
def extract(begin, end, data):
print(begin)
Ta=0
Td=0
Tc=0
Ti=0
S=0
vmax=0
amax=0
amin=0
jiasusum=0
jiansusum=0
xmax=0
xjz=0
ymax=0
yjz=0
zmax=0
zjz=0
zsmax=0
zsjz=0
njmax=0
njjz=0
yhmax=0
yhjz=0
tbmax=0
tbjz=0
rbmax=0
rbjz=0
fhmax=0
fhjz=0
jqmax=0
jqjz=0
jsstd=0
for i in range(begin,end+1):
jsstd+=data[i][5]**2
if data[i][5] > 0.1:
if (i>begin and data[i-1][5] > 0.1) or (i 0.1):
Ta += 1
jiasusum += data[i][5]
elif data[i][5] < -0.1:
if (i>begin and data[i-1][5] < -0.1) or (i 问题三行驶工况构建 Python 代码
import numpy as np
import pandas as pd
def extract(begin, end, data):
print(begin)
Ta,Td,Tc,Ti,S=0,0,0,0,0
vmax,amax,amin=0,0,0
jiasusum,jiansusum=0,0
xmax,xjz=0,0
ymax,yjz=0,0
zmax,zjz=0,0
zsmax,zsjz=0,0
njmax,njjz=0,0
yhmax,yhjz=0,0
tbmax,tbjz=0,0
rbmax,rbjz=0,0
fhmax,fhjz=0,0
jqmax,jqjz=0,0
jsstd=0,0
for i in range(begin,end+1):
jsstd+=data[i][5]**2
if data[i][5] > 0.1:
if (i>begin and data[i-1][5] > 0.1) or (i 0.1):
Ta += 1
jiasusum += data[i][5]
elif data[i][5] < -0.1:
if (i>begin and data[i-1][5] < -0.1) or (i