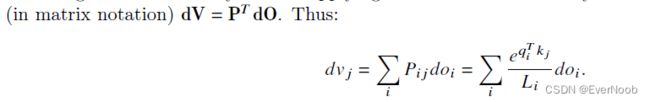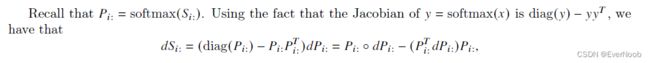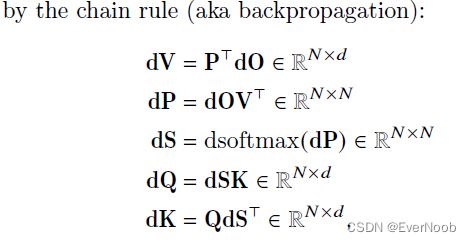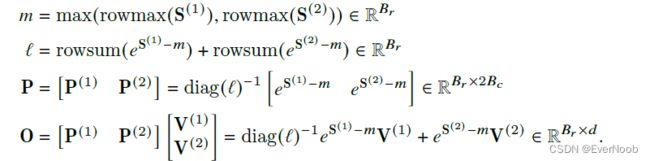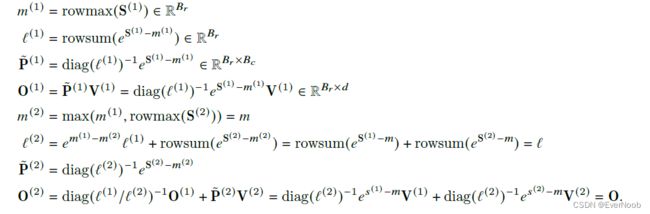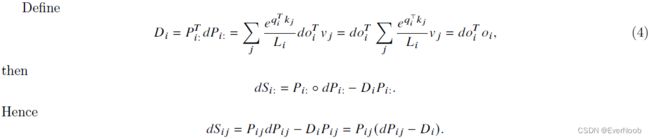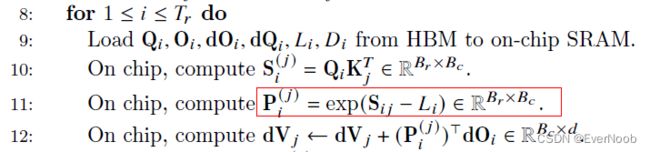FlashAttention-2

FlashAttention is a fusion trick, which merges multiple operational steps (ops) in the attention layers of transformer networks to achieve better end2end result; the performance gain is mainly from better memory reuse given the vanilla version being memory bounded.

see: FlashAttention_EverNoob的博客-CSDN博客

With the advent of industrial deployment of LLMs, mainly featuring longer and longer sequence/context length, the author further enhanced their method to achieve greater speed up (on NV A100).

List of resources:

brief intro. article: Stanford CRFM 

paper: https://arxiv.org/pdf/2307.08691.pdf

github: GitHub - Dao-AILab/flash-attention: Fast and memory-efficient exact attention 

FlashAttention-2: Faster Attention with Better Parallelism and Work Partitioning

Overview

based on intro. article

FlashAttention Recap

FlashAttention is an algorithm that reorders the attention computation and leverages classical techniques (tiling, recomputation) to significantly speed it up and reduce memory usage from quadratic to linear in sequence length. Tiling means that we load blocks of inputs from HBM (GPU memory) to SRAM (fast cache), perform attention with respect to that block, and update the output in HBM. By not writing the large intermediate attention matrices to HBM, we reduce the amount of memory reads/writes, which brings 2-4x wallclock time speedup.

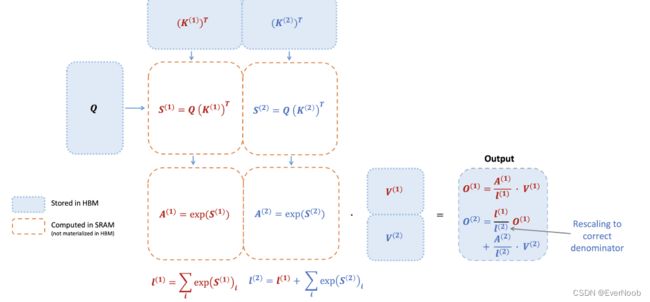
Here we show a diagram of FlashAttention forward pass: with tiling and softmax rescaling, we operate by blocks and avoid having to read/write from HBM, while obtaining the correct output with no approximation.

However, FlashAttention still has some inefficiency due to suboptimal work partitioning between different thread blocks and warps on the GPU, causing either low-occupancy or unnecessary shared memory reads/writes.

3 Main Improvements

Higher GEMM%

rebalance workload to favor the Tensore Cores, which process matmul ops. with much higher efficiency than SIMT units.

As an example, the A100 GPU has a max theoretical throughput of 312 TFLOPs/s of FP16/BF16 matmul, but only 19.5 TFLOPs/s of non-matmul FP32. 

Better Parallelism

let B, N, S, H be the batch count, head count, sequence length and head dimension/size respectively;

the previous work only featured multiprocessor parallelism on B*N, i.e. 1 core or thread block per head. Each thread block is scheduled to run on a streaming multiprocessor (SM), and there are 108 of these SMs on an A100 GPU for example. 

For a shape with relatively small BN and large S, this setup clearly cannot harness the full capacity of the device, and V2.0 "additionally parallelize over the sequence length dimension"; since we expect the tiling dim. to be much smaller than S, and we get a total of sqr(S/tile_dim) tasks, the new mp. para. dim. features much better workload balance and utilization rate of the device and achieves better speedup.

Better Work Partitioning

This balancing specifically deals with intra-block or inter-warp workload balance.

Even within each thread block, we also have to decide how to partition the work between different warps (a group of 32 threads working together). We typically use 4 or 8 warps per thread block, and the partitioning scheme is described below. We improve this partitioning in FlashAttention-2 to reduce the amount of synchronization and communication between different warps, resulting in less shared memory reads/writes.

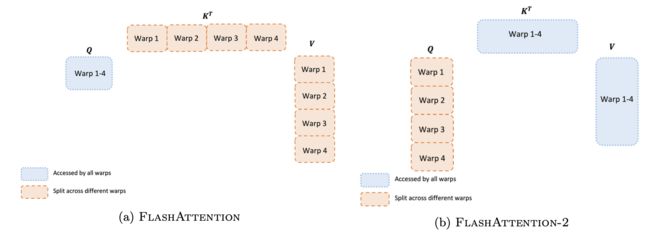
For each block, FlashAttention splits K and V across 4 warps while keeping Q accessible by all warps. This is referred to as the “sliced-K” scheme. However, this is inefficient since all warps need to write their intermediate results out to shared memory, synchronize, then add up the intermediate results. These shared memory reads/writes slow down the forward pass in FlashAttention.

In FlashAttention-2, we instead split Q across 4 warps while keeping K and V accessible by all warps. After each warp performs matrix multiply to get a slice of Q K^T, they just need to multiply with the shared slice of V to get their corresponding slice of the output. There is no need for communication between warps. The reduction in shared memory reads/writes yields speedup

New features: head dimensions up to 256, multi-query attention

FlashAttention only supported head dimensions up to 128, which works for most models but a few were left out. FlashAttention-2 now supports head dimension up to 256, which means that models such as GPT-J, CodeGen and CodeGen2, and StableDiffusion 1.x can use FlashAttention-2 to get speedup and memory saving.

This new version also supports multi-query attention (MQA) as well as grouped-query attention (GQA). These are variants of attention where multiple heads of query attend to the same head of key and value, in order to reduce the size of KV cache during inference and can lead to significantly higher inference throughput.

Base Attention

recall from V1.0 paper:

and 

 by reverse mode of auto-diff, see Automatic Differentiation_EverNoob的博客-CSDN博客

get:

further

==> partial_phi / partial_S = partial_phi / partial_P * partial_P / partial_S

for the computation of the Jacobian of sftmax, see https://towardsdatascience.com/derivative-of-the-softmax-function-and-the-categorical-cross-entropy-loss-ffceefc081d1

and overall we have: 

FlashAttention 1.0

Foward Pass

FlashAttention applies the classical technique of tiling to reduce memory IOs, by (1) loading blocks of inputs from HBM to SRAM, (2) computing attention with respect to that block, and then (3) updating the output without writing the large intermediate matrices S and P to HBM. As the softmax couples entire rows or blocks of row, online softmax [11, 13] can split the attention computation into blocks, and rescale the output of each block to finally get the right result (with no approximation). By significantly reducing the amount of memory reads/writes, FlashAttention yields 2-4× wall-clock speedup over optimized baseline attention implementations.

online softmax and rescaling:

compute:

Online softmax instead computes “local” softmax with respect to each block and rescale to get the right output at the end:

==> diag(l)^-1 translates to a pointwise div(brc(l))

Figure 1: Diagram of how FlashAttention forward pass is performed, when the key K is partitioned into two blocks and the value V is also partitioned into two blocks. By computing attention with respect to each block and rescaling the output, we get the right answer at the end, while avoiding expensive memory reads/writes of the intermediate matrices S and P. We simplify the diagram, omitting the step in softmax that subtracts each element by the row-wise max.

Backward Pass

In the backward pass, by re-computing the values of the attention matrices S and P once blocks of inputs Q,K,V are already loaded to SRAM, FlashAttention avoids having to store large intermediate values. By not having to save the large matrices S and P of size × , FlashAttention yields 10-20× memory saving depending on sequence length (memory required in linear in sequence length instead of quadratic).

we need to compute dQKV by:

==> recompute P: Q, K, m, l -> P = exp(Q*K - m) / l ==>use * for matmul

==> compute dP = V*dO

with

==> compute D = rowsum(dot(O, dO))

==> compute dS = dot(P, (dP - D))

==> compute dQ = dS * K

==> compute dK = dS * Q

see V1.0 paper for detailed algorithm.

FlashAttention 2.0

Algorithm

We tweak the algorithm from FlashAttention to reduce the number of non-matmul FLOPs. The A100 GPU has a max theoretical throughput of 312 TFLOPs/s of FP16/BF16 matmul, but only 19.5 TFLOPs/s of non-matmul FP32. To maintain high throughput (e.g., more than 50% of the maximum theoretical TFLOPs/s), we want to spend as much time on matmul FLOPs as possible.

We revisit the online softmax trick as shown in Section 2.3 and make two minor tweaks to reduce non-matmul FLOPs:

l_last is obviously the cummulative results, which revise the forward pass into:

it exploits the recomputation in backpass:

but it's truly minor, since m, l are only O(n) in storage, and we only shortened backpass by 1 div.

another point to notice is step 4:

in dense, B*N multicore tiling version of FA bp, it is better to compute inside traversal per initial block per row, but for sparse and seq_len dim. parallelism this reuse is hard to manage if possible at all, hence compute entire D in advance an reduce overall computation significantly. Another problem, however, arise, if mac unit (TensorCore of A100) can be executed in parallel with vector unit (SIMT of A100), since recomputation of D is likely free in terms of time.

Parallelism

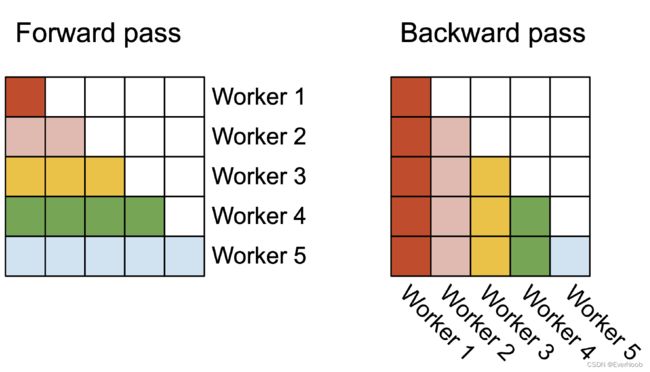
The first version of FlashAttention parallelizes over batch size and number of heads. We use 1 thread block to process one attention head, and there are overall batch size · number of heads thread blocks. Each thread block is scheduled to run on a streaming multiprocessor (SM), and there are 108 of these SMs on an A100 GPU for example. This scheduling is efficient when this number is large (say ≥ 80), since we can effectively use almost all of the compute resources on the GPU. In the case of long sequences (which usually means small batch sizes or small number of heads), to make better use of the multiprocessors on the GPU, we now additionally parallelize over the sequence length dimension. This results in significant speedup for this regime.

Figure 2: In the forward pass (left), we parallelize the workers (thread blocks) where each worker takes care of a block of rows of the attention matrix. In the backward pass (right), each worker takes care of a block of columns of the attention matrix.

Work Partitioning Between Warps

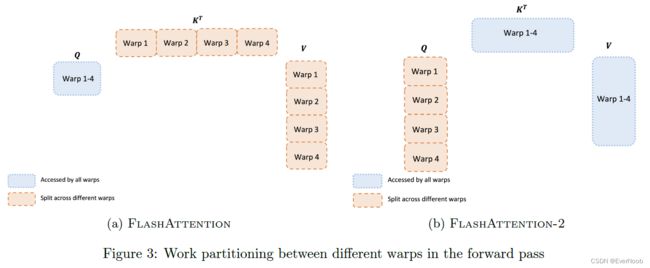
Forward pass.

For each block, FlashAttention splits K and V across 4 warps while keeping Q accessible by all warps. Each warp multiplies to get a slice of QK, then they need to multiply with a slice of V and communicate to add up the result. This is referred to as the “split-K” scheme. However, this is inefficient since all warps need to write their intermediate results out to shared memory, synchronize, then add up the intermediate results. These shared memory reads/writes slow down the forward pass in FlashAttention. In FlashAttention-2, we instead split Q across 4 warps while keeping K and V accessible by all warps. After each warp performs matrix multiply to get a slice of QK⊤, they just need to multiply with their shared slice of V to get their corresponding slice of the output. There is no need for  communication between warps. The reduction in shared memory reads/writes yields speedup (Section 4).

 Backward pass.

Similarly for the backward pass, we choose to partition the warps to avoid the “split-K” scheme. However, it still requires some synchronization due to the more complicated dependency between all the different inputs and gradients Q,K,V,O, dO, dQ, dK, dV. Nevertheless, avoiding “split-K” reduces shared memory reads/writes and again yields speedup (Section 4).

Tuning block sizes

Increasing block sizes generally reduces shared memory loads/stores, but increases the number of registers required and the total amount of shared memory. Past a certain block size, register spilling causes significant slowdown, or the amount of shared memory required is larger than what the GPU has available, and the kernel cannot run at all. Typically we choose blocks of size {64, 128} × {64, 128}, depending on the head dimension and the device shared memory size. We manually tune for each head dimensions since there are essentially only 4 choices for block sizes, but this could benefit from auto-tuning to avoid this manual labor. We leave this to future work.