数据结构---线性表

线性表

代码主要参考 严蔚敏《数据结构（c语言版）》，有部分改动

线性表的定义

定义

• 线性表是具有相同的数据类型的n(n >= 0)个数据元素的有限序列，当n=0时线性表为一个空表
• 用L表示线性表则 L = （a1,a2,a3,…,an
  • a1为表头元素，an为表尾元素
  • a1无直接前驱，an无直接后继

特点

• 表中元素个数有限
• 表中元素具有逻辑上的顺序，表中元素有先后次序
• 表中元素都是数据元素
• 表中元素的数据类型都相同，每个元素占的空间大小一致

要点

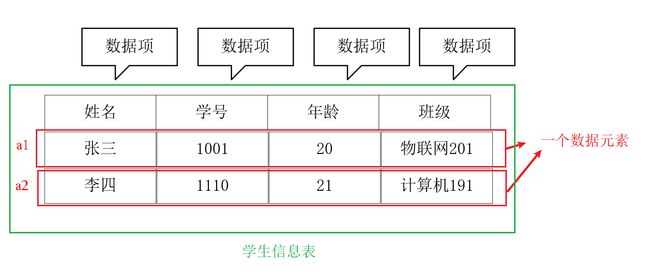
数据项、数据元素、线性表的关系

线性表由若干个数据元素组成，而数据元素又由若干个数据项组成，数据项是数据的不可分割的最小单位。

其中姓名，学号等就是数据项

线性表的顺序表示

顺序表的定义

顺序表是指用一组地址连续的存储单元依次存储信息表中的数据元素，从而使得逻辑相邻的两个元素在物理位置上也相邻

预先定义（为了代码可以运行）

#define True 1
#define False 0
#define OK 1
#define ERROR 0
#define INFEASIBLE -1
#define OVERFLOW -2
typedef int Status;

第n个元素的内存地址表示为

 LOC(A) + (n-1)*sizeof(ElemType)

假定线性表的元素类型为ElemType,则线性表的顺序存储类型描述为

typedef int  ElemType  ;
#define MaxSize 50
typedef struct{
    ElemType data[MaxSize];
    int length;
}SqList;

一维数组可以是静态分配的，也可以是动态分配的。静态分配后大小和空间都固定了，下面使用动态分配的形式

typedef int  ElemType  ;
#define InitSize 100 //表长度的初始大小定义
#define ListIncreasement 10 //线性表存储空间的分配增量
typedef struct {
    ElemType *data;
    int MaxSize,length;
}SeqList;

顺序表的初始化

顺序表的初始化,&是C++的引用，可以使用指针代替

Status InitList(SeqList &L){
    L.data = (ElemType *) malloc(InitSize * sizeof(ElemType));
    if(! L.data) exit(OVERFLOW);//存储分配失败
    L.length = 0;
    L.MaxSize = InitSize;
    return OK;
}

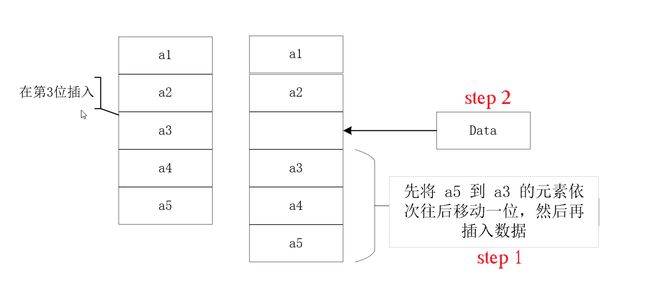
顺序表的插入

在顺序表L的第i(1<= i <= L.length +1)个位置插入新元素 e，需要将第 n 个至第 i (共 n-i+1)个元素向后移动一个位置 【最后一个到倒数第n-i+i个元素向后移动一位】。

Status ListInsert(SeqList &L,int i , ElemType e){
    ElemType * newbase;
    if(i<1 || i > L.length+1)//判断i是否合法
        return ERROR;
    if(L.length >= L.MaxSize){ //当前存储空间已满，可直接返回false
        newbase = (ElemType *)realloc(L.data,(L.MaxSize+ListIncreasement)*sizeof(ElemType));
        if(!newbase){//存储分配失败
            exit(OVERFLOW);
        }
        L.data = newbase; //新基址
        L.MaxSize += ListIncreasement;
    }
    //移动元素
    for(int j = L.length; j>=i ;j--){
        L.data[j] = L.data[j-1];
    }
    L.data[i-1] = e;//插入e
    L.length++;//增加长度
    return OK;
}

最好情况：在表尾插入，时间复杂度为O(1)

最坏情况：在表头插入，时间复杂度为O（n）

平均情况：假设Pi(Pi=1/(n+1))是在第i个位置上插入一个节点的概率，则平均移动次数为
$$\sum _{i=1}^{n+1}{p}_i(n-i+1)=\sum _{i=1}^{n+1}\frac{1}{n+1}(n-i+1)=\frac{1}{n+1}\frac{n(n+1)}{2}=\frac{n}{2}$$

顺序表的删除

删除顺序表L的第i(1< i <= L.length)个位置的元素，需要将第i+1个至第n(共n-1)个元素依次向前移动一个位置。

Status ListDelete(SeqList &L,int i , ElemType &e){
    if(i<1|| i>L.length)  return ERROR;//判断删除位置是否合法
    e = L.data[i-1];
    //依次前移，把第i个元素覆盖，相当于是删除
    for(int j = i ; j < L.length ; j ++){
        L.data[j-1] = L.data[j];
    }
    L.length--;//长度减一
    return OK;
}

最好情况：在表尾删除，时间复杂度为O(1)

最坏情况：在表头删除，时间复杂度为O（n）

平均情况：假设Pi(Pi=1/(n))是删除在第i个位置上一个节点的概率，则平均移动次数为
$$\sum _{i=1}^{n+1}{p}_i(n-1)=\sum _{i=1}^{n+1}\frac{1}{n}(n-i)=\frac{1}{n}\frac{n(n-1)}{2}=\frac{n-1}{2}$$

按值查找

查找第一个与e相等的元素，并返回其位序。

int LocateElem(SeqList &L,ElemType e){
    for(int i = 0 ; i < L.length; i++){
        if (L.data[i] == e){
            return i+1;//下标为i的元素值等于e,则位序为i+1
        }
    }
    return ERROR;//查找失败
}

平均情况：
$$\sum _{i=1}^{n+1}{p}_i\times i=\sum _{i=1}^{n+1}\frac{1}{n}\times i=\frac{1}{n}\frac{n(n+1)}{2}=\frac{n+1}{2}$$

顺序表例题

1、从顺序表中删除具有最小值的元素(假设唯一)并由函数返回被删除的元素的值，空出的位由最后一个元素来填补，若顺序表为空则显示出错误并退出运行。

bool ListMinElem(SeqList &L,ElemType &e){
    if(L.length<1){
        return false ;
    }
    int pos;
    e = L.data[0];
    for(int i =0; i < L.length ; i++){
        if(L.data[i]<e){
            e=L.data[i];   //e就是存的最小值
            pos = i;
        }
    }
    L.data[pos] = L.data[L.length-1]; //用最后一个元素的值填充最小元素的位置
    L.length--; //长度减一相当于删除了最后一个元素
    return true ;
}

2、设计一个高效算法，将顺序表L的所有元素逆置，要求算法的空间复杂度为O（1）

void ListReverse(SeqList &L){
    ElemType temp;
    for(int i = 0; i < L.length/2; i++){
        temp = L.data[i]; //保存前面的元素
        L.data[i] = L.data[L.length - 1 -i]; //和后面的元素交换
        L.data[L.length - 1 -i] = temp;
    }
}

3、对长度为n的顺序表L，编写一个时间复杂度为O(n),空间复杂度为O（1）的算法，该算法删除线性表中所有值为X的元素。

void ListDeleteX(SeqList &L , ElemType x){
    int k = 0 ;//记录L不等于x的元素的个数
    for ( int i = 0; i < L.length; i++){
        if(L.data[i] != x){
            L.data[k] = L.data[i];//将不等于x的元素向前移
            k++;//长度增加
        }
    }
    L.length = k;//将最后的不等于x的个数赋值给L.length
}

线性表的链式表示

链表的定义

用一组任意的存储单元存储线性表的数据元素（地址不连续），因为地址不连续，所以链表的数据结构中需要存放下一个节点的地址，所以通常一个结点有两个部分（数据域和指针域）

一般形式

一般需要一个头结点来访问整个链表，头结点的数据域一般不存数据。

typedef struct LNode{
    ElemType data;
    struct LNode *next;
}LNode;

链表的初始化

Status InitLinkList(LinkList &L){
    L = (LinkList) malloc(sizeof(LNode));
    if(!L) exit(OVERFLOW);
    return OK;
}

链表的插入

插入时先将要插入的节点P的指针域赋值为上一个节点S的指针域，

P->next = S->next;
S->next = P;

Status ListInsert_L(LinkList &L,int i,ElemType e){
    //在第i个位置插入
    LinkList P = L;
    int j = 0 ;
    while(P && j < i-1){
        P = P->next;//寻找到第i-1一个结点
        j++;
    }
    if(!P || j > i - 1) return ERROR;//!P是判断是否超出表的长度， j > i -1 判断输入的位置是否小于1
    LinkList S = (LinkList) malloc(sizeof(LNode));
    if(!S) exit(OVERFLOW);
    S->data = e;
    S->next = P->next;
    P->next = S;
    return OK;
}

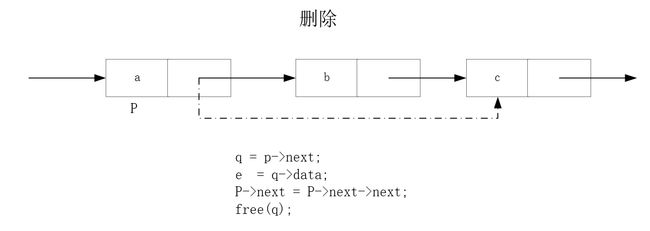
链表的删除

同插入一样，先找到 第 i-1个元素位置，然后用一个变量S保存要删除的节点，再将P的next指向P的next的next；然后用free(S)释放掉删除元素的空间

Status ListDelete_L(LinkList &L,int i,ElemType &e){
    //删除第i个位置的元素
    LinkList p = L,q;
    int j = 0;
    while(p->next && j < i-1){//p->next指向第一个元素，j处于第0个元素的位置，为了找到第 i - 1 个元素；
        p = p->next;
        j++;
    }
    if(!(p->next) || j > i-1) return ERROR;//删除位置不合理
    q  = p->next;
    p->next = q->next;
    e = q->data;
    free(q);
    return OK;
}

头插法建立单链表

void CreateList_L(LinkList &L,int n){
    //n是个数
    L = (LinkList) malloc(sizeof(LNode));
    if(!L) exit(OVERFLOW);
    L->next = NULL;

    for(int i = n ; i > 0 ; i--){
        LinkList p = (LinkList) malloc(sizeof(LNode));//创建新结点
        if(!p) exit(OVERFLOW);
        scanf("%d",&p->data);//获取值
        p->next = L->next;
        L->next = p;//新结点插入到表头
    }
}

尾插法

Status ListInsertTail_L(LinkList &L,ElemType e){
    LinkList p = L;
    while (p->next != NULL)  p = p->next;//获取到最后一个节点
    LinkList newNode = (LinkList) malloc(sizeof(LNode));//创建新结点
    if(!newNode) exit(OVERFLOW);
    newNode->data = e;
    newNode->next = NULL;
    p->next = newNode;//插入到最后
    return OK;
}

链表的合并

了解

void MergeList_L(LinkList &La,LinkList &Lb,LinkList &Lc){
    //已知单链表La,Lb的元素按值非递减排列
    //归并La,Lb得到Lc也按值非递减排列
    LinkList pa,pb,pc;
    pa = La->next;
    pb = Lb->next;
    Lc = pc = La;
    while (pa&&pb){
        if(pa->data <= pb->data){
            pc->next = pa;pc = pa;pa = pa->next;
        } else{
            pc->next = pb; pc = pb; pb = pb->next;
        }
        pc->next = pa ? pa : pb;//插入剩下的片段
    }
    free(Lb);
}

双向链表

在单链表的基础上增加了一个指向前一个节点的指针域。

typedef struct DuLNode{
    ElemType data;
    struct DuLNode * prior;
    struct DuLNode * next;
}DuLNode,*DuLinkList;

双向链表应用–约瑟夫算法

#include 
using namespace std;
const int N = 20;
typedef struct node {
	int id;
	struct node *next;
	struct node *pre;
}Node, *pNode;

//创建一个约瑟夫环并获取到他的头结点。
pNode RingConstruct(int n) {

	pNode head, p, q; // head为头结点
	head = (pNode)malloc(sizeof(Node));//创建第一个结点
	head->id = 1; //ID为1
	p = head;
	for (int i = 2; i <= n; i++) {//创建n-1个结点，
		q = (pNode)malloc(sizeof(Node));
		q->id = i;
		p->next = q;
		q->pre = p;
		p = p->next;
	}
	p->next = head;//最后一个结点的next域连接到头结点
	head->pre = p;//头结点的pre域连接到尾结点
	return head;
}

//传入报数的次数序号，返回此次报送的上限，简单来说就是报几次数。相当于每个人手里拿了一个号码牌
int bounMachine(int order) {
	int boundList[4] = { 3,5,7,13 };
	return boundList[(order - 1) % 4];
}

//从该结点起，转bound次后的结点，bound参数由boundMachine提供
pNode count(pNode first, int bound) {
	pNode q;
	q = first;
	for (int i = 2; i <= bound; i++) {//从第二个人开始计数。
		q = q->next;
	}
	return q;
}

//将currentNode从环中删除，并返回被删除结点的下一结点
pNode removeNode(pNode currentNode) {
	pNode first = currentNode->next;//删除后，first为当前结点的下一个结点
	currentNode->pre->next = currentNode->next;
	first->pre = currentNode->pre;
	cout << currentNode->id << " ";//输出当前删除编号
	free(currentNode);
	return first;
}

int main() {
	//first为没趟的起始结点通过函数removeNode提供下一次起始地址;
	// toRemove为要删除的结点通过count提供;
	pNode first, toRemove;

	first = RingConstruct(N);

	for (int i = 1; i <= N; i++) {
		toRemove = count(first, bounMachine(i));
		first = removeNode(toRemove);
	}
 
}