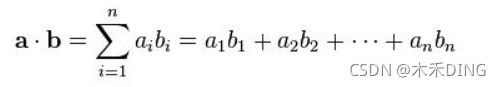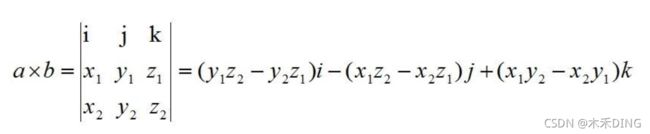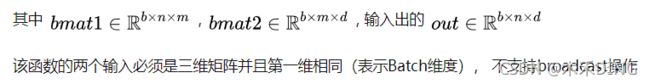pytorch 矩阵和向量乘法
向量
- 点乘：又叫做点积、内积、数量积、标量积，向量a[a1,a2,...,an]和向量b[b1,b2b...,bn]点乘的结果是一个标量，记作a.b；
得到一个值。
- 叉乘：又叫向量积、外积、叉积，叉乘，向量a[x1,y1,z1]和向量b[x2,y2,z2]叉乘的运算结果是一个向量，并且两个向量的叉积与这两个向量组成的坐标平面垂直，记作axb；
得到一个向量。
a=torch.tensor([1,2,3])
b=torch.tensor([2,3,4])
print(torch.dot(a,b))
print(torch.cross(a,b))
# tensor(20)
# tensor([-1, 2, -1])矩阵
- 矩阵点乘（逐元素乘，Element-wise）：是矩阵各个对应元素相乘, 这个时候要求两个矩阵必须同样大小。
- 矩阵叉乘（就是矩阵乘法）：矩阵的乘法就是矩阵a的第m行乘以矩阵b的第n列，各个元素对应相乘然后求和作为第m行n列元素的值。
1. 二维矩阵乘法 torch.mm()
torch.mm(mat1, mat2, out=None)
2. 三维带batch的矩阵乘法 torch.bmm()
由于神经网络训练一般采用mini-batch，经常输入的时三维带batch的矩阵，所以提供
torch.bmm(bmat1, bmat2, out=None)
一般用的比较少，仅仅是模型一个batch训练的时候使用。
3. 多维矩阵乘法 torch.matmul()
torch.matmul(input, other, out=None)支持broadcast操作，一般矩阵乘法，推荐使用这个matmul。针对多维数据 matmul() 乘法，可以认为该乘法使用使用两个参数的后两个维度来计算，其他的维度都可以认为是batch维度。假设两个输入的维度分别是input(1000×500×99×11), other(500×11×99)那么我们可以认为torch.matmul(input, other, out=None)乘法首先是进行后两位矩阵乘法得到(99×11)×(11×99) ⇒(99×99) ，然后分析两个参数的batch size分别是 (1000×500) 和（ 500x1) , 可以广播成为(1000×500)， 因此最终输出的维度是(1000×500×99×99)。
4. 矩阵逐元素(Element-wise)乘法 torch.mul()
torch.mul(mat1, other, out=None)其中 other 乘数可以是标量，也可以是任意维度的矩阵， 只要满足最终相乘是可以broadcast的即可。
5. dot 函数
对于秩为1的数组，执行对应位置相乘，然后再相加，等价于向量的点乘；
对于秩不为1的二维数组，执行矩阵乘法运算，等价于矩阵的叉乘；
6. * 和 @
* 代表的是矩阵逐元素乘
@ 代表的是 矩阵乘法
x=torch.tensor([[1,2],[3,4]])
y=torch.tensor([[1,2],[3,4]])
print(x*y)
print(x@y)
# tensor([[ 1, 4],
# [ 9, 16]])
# tensor([[ 7, 10],
# [15, 22]])经验
1. 把向量 看成 1*n 的矩阵,不过需要采用 unsqueeze() 函数来增加一下维度。
转置的话 ，一般采用 a.t() 或者 a.transpose(0,1)
2. 矩阵点乘 用 torch.mul
3. 矩阵乘法 用 torch.matmul
import torch
a=torch.tensor([1,2,3]) # 1*3
c=torch.tensor([[1,2,3],[4,5,6]]) # 2*3
print(torch.mul(a,c))
print(torch.matmul(c,a))
#tensor([[ 1, 4, 9],
# [ 4, 10, 18]])
#tensor([14, 32])