相关网站:http://www.ai4g.com
PART I AI AND GAMES
CHAPTER1 INTRODUCTION
CHAPTER2 GAME AI
PART II TECHNIQUES
CHAPTER3 MOVEMENT
CHAPTER4 PATHFINDING
CHAPTER5 DECISION MAKING
CHAPTER6 TACTICAL AND STRATEGIC AI
CHAPTER7 LEARNING
CHAPTER8 BOARD GAMES
PART III SUPPORTING TECHNOLOGIES
CHAPTER9 EXECUTION MANAGEMENT
CHAPTER10 WORLD INTERFACING
CHAPTER11 TOOLS AND CONTENT CREATION
CHAPTER12 DESIGNING GAME AI
CHAPTER13 AI-BASED GAME GENRES
References
CHAPTER1 INTRODUCTION
1.1 WHAT Is AI?
1.1.1 Academic AI
1.1.2 Game AI
1.2 MODEL OF GAME AI
1.2.1 Movement
1.2.2 Decision Making
1.2.3 Strategy
1.2.4 Infrastructure
1.2.5 Agent-Based AI
1.2.6 In the Book
1.3 ALGORITHMS,DATA STRUCTURES,AND REPRESENTATIONS
1.3.1 Algorithms
1.3.2 Representations
1.4 ON THE WEBSITE
1.4.1 Programs
1.4.2 Libraries
1.5 LAYOUT OF THE BOOK
CHAPTER2 GAME AI
2.1 THE COMPLEXITY FALLACY
2.1.1 When Simple Things Look Good
2.1.2 When Complex Things Look Bad
2.1.3 The Perception Window
2.1.4 Changes of Behavior
2.2 THE KIND OF AI IN GAMES
2.2.1 Hacks
2.2.2 Heuristics
2.2.3 Algorithms
2.3 SPEED AND MEMORY
2.3.1 Processor Issues
2.3.2 Memory Concerns
2.3.3 PC Constraints
2.3.4 Console Constraints
2.4 THE AI ENGINE
2.4.1 Structure of an AI Engine
2.4.2 Toolchain Concerns
2.4.3 Putting It All Together
CHAPTER3 MOVEMENT
One of the most fundamental requirements of AI is to move characters around in the game sensibly.
There is also some degree of overlap between AI and animation; animation is also about movement. This chapter looks at large-scale movement: the movement of characters around the game level, rather than movement of their limbs or faces. The dividing line isn't always clear, however. In many games animation can take control over a character, including some large-scale movement. In-engine cutscenes, completely animated, are increasingly being merged into gameplay; however, they are not AI driven and therefore aren't covered here.
3.1 THE BASICS OF MOVEMENT ALGORITHMS
Each character has a current position and possibly additional physical properties that control its movement. A movement algorithm is designed to use these properties to work out where the character should be next.
All movement algorithms have this same basic form. They take geometric data about their own state and the state of the world, and they come up with a geometric output representing the movement they would like to make.
Some movement algorithms require very little input: the position of the character an the position of an enemy to chase, for example. Others require a lot of interaction with the game state and the level geometry. A movement algorithm that avoids bumping into walls, for example, needs to have access to the geometry of the wall to check for potential collisions.
The output can vary too. In most games it is normal to have movement algorithms ouput a desired velocity. A character might see its enemy immediately west of it, for example, and respond that its movement should be westward at full speed. Often, characters in older games only had two speeds: stationary and running(with maybe a walk speed in there, too). So the output was simply a direction to move in. This is kinematic movement; it does not account for how characters accelerate and slow down.
Recently, there has been a lot of interest in "steering behaviors." Streering behaviors is the name given by Craig Reynolds to his movement algorithms; they are not kinematic, but dynamic. Dynamic movement takes account of the current motion of the character. A dynamci algorithm typically needs to know the current velocities of the character as well as its position. A dynamic algorithm outputs forces or accelerations with the aim of changing the velocity of the character.
Dynamics adds an extra layer of complexity. Let's say your character needs to move from one place to another. A kinematic algorithm simply gives the direction to the target; you move in that direction until you arrive, whereupon the algorithm returns no direction: you've arrived.A dynamic movement algorithm needs to work harder. If first needs to accelerate in the right direction, and then as it gets near its target it needs to accelerate in the opposite direction, so its speed decrease as precisly the correct rate to slow it to a stop at exactly the right place. Because Craig's work is so well known, in the rest of this chapter we'll usually follow the most common terminiology and refer to all dynamic movement as steering behaviors.
Craig Reynolds also invented the flocking algorithm used in countless films and games to animate flocks of birds or herds of other animals. We'll look at this algorithm later in the chapter. Because flocking is the most famous steering behavior, all steering(in fact, all movement) algorithms are sometimes wrongly called "flocking".
3.1.1 Two-Dimensional Movement
[Characters as Points]
Although a character usually consists of a three-dimensional(3D) model that occupies some space in the game world, many movement algorithms assume that the character can be treated as a single point. Collision detection, obstacle avoidance, and some other algorithms use the size of the character to influence their results, but movement itself assumes the chracter is at a single point.
This is a process similar to that used by physics programmers who treat objects in the game as a "rigid body" located at its center of mass. Collision detection and other forces can be applied to anywhere on the object, but the algorithm that determines the movement of the object converts them so it can deal only with the center of mass.
3.1.2 Statics
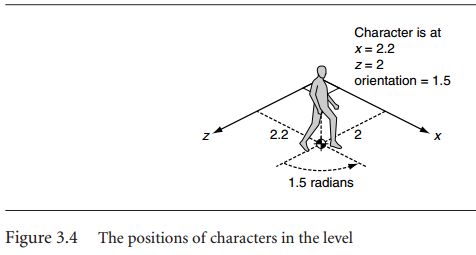
Characters in two dimensions have two linear coordinates representing the position of the object. These cooridnates are relative to two world axes that lie perpendicular to the direction of gravity and perpendicular to each other. This set of reference axes is termed the orthonormal basis fo the 2D space
In addition to the two linear coordinates, an object facing in any direction has one orientation value. The orientation value represents an angle from a reference axis.
Algorithm or equations that manipulate this data are called static because the data do not contain any information about the movement of a character.
We will use the term orientation throughout this chapter to mean the direction in which a character is facing. When it comes to rendering characters, we will make them appear to face one direction by rotating them (using a rotation matrix). Because of this, some developers refer to orientation as rotation. We will use rotation in this chapter only to mean the process of changing orientation; it is an active process.
struct Static: position # a 2D vector orientation # a single floating point value
In two dimensions we need only an angle to represent orientation. This is the scalar representation. The angle is measured from the positive z-axis, in a right-handed direction about the positive y-axis(counterclockwise as you look down on the x-z plane from above)
It is more convenient in may circumstances to use a vector representation of orientation. In this case the vector is a unit vector in the direction that the character is facing. This can be directly calculated from the scalar orientation using simple trigonometry: where ws is the orientation as a scalar, and wv is the orientation expressed as a vector.
3.1.3 Kinematics
So far each character had two associated pieces of information: its position and its orientation. We can create movement algorithms to calculate a target velocity based on position and orientation alone, allowing the output velocity to change instantly
While this is fine for many games, it can look unrealistic. A consequence of Newton's laws of motion is that velocities cannot change instantly in the real world. If a character is moving in one direction and then instantly changes direction or speed, it will look odd. To make smooth motion or to cope with character thata can't accelerate very quickly, we need either to use some kind of smoothing algorithm or to take account of the current velocity and use accelerations to change it.
To support this, the character keeps track of its current velocity as well as position. Algorithms can then operate to change the velocity slightly at each time frame , giving a smooth motion.
Characters need to keep track of both theire linear and their angular velocities. Linear velocity has both x and z components, the speed of the character in each of the axes in the orthonormal basis. If we are working in 2.5D, then there will be three linear velocity components, in x, y, and z.
The angular velocity represents how fast the character's orientation is changing. This is given by a single value: the number of radians per second that the orientation is changing.
We will call angular velocity rotation, since rotation suggests motion. Linear velocity will normally be referred to as simply velocity. We can therefore represent all the kinematic data for a character(i.e., its movement and position) in one structure.
struct Kinematic: positon # a 2 or 3D vector orientation # a single floating point value velocity # another 2 or 3D vector rotation # a single floating point value
Streering behaviors operate with these kinematic data.They return accelerations that will change the velocities of a character in order to move them around the level. There output is a set of accelerations:
struct SteeringOutput: linear # a 2 or 3D vector angular # a single floating point value
Independent Facing
Notice that there is nothing to connect the direction that a character is moving and the direction it is facing. A character can be oriented along the x-axis but be traveling directly along the z-axis. Most game characters should not behave in this way; they should orient themselves so they move in the direction they are facing.
Many steering behaviors ignore facing altogether. They operate directly on the linear components of the character's data. In these cases the orientation should be updated so that it matches the direction of motion.
This can be achieved by directly setting the orientation to the direction of motion, but this can mean the orientation chagnes abruptly.
A better solution is to move it a proportion of the way toward the desired direction: to smooth the motion over many frames.
Updating Position and Orientation
struct Kinematic: ... Member data as before ... def update(steering, time): # Update the position and orientation position += velocity * time + 0.5 * steering.linear * time * time orientation += rotation * time + 0.5 * steering.angular * time * time # and the velocity and rotation velocity += steering.linear * time orientation += steering.angular * time
The updates use high-school physics equations for motion. If the frame rate is high, then the update time passed to this function is likely to be very small. The square of this time is likely to be even smaller. and so the contribution of acceleration to position and orientation will be tiny. It is more common to see these terms removed from the update algorithm, to give what's known as the Newton-Euler-1 integration update:
struct Kinematic: ... Member data as before ... def Update(steering, time): #Update the position and orientation position += velocity * time orientation += rotation * time # and the velocity and rotation velocity += steering.linear * time orientation + steering.angular * time
Variable Frame Rates
Note that we have assumed that velocities are given in units per second rather than per frame. Older games often used per-frame velocities, but that practice has largely died out. Almost all games(even those on a console) are now written to support variable frame rates, so an explicit update time is used.
If the character is known to be moving at 1 meter per second and the last frame was of 20 milliseconds' duration, then they will need to move 20 millimeters
Forces and Actuation
In the real world we can't simply apply an acceleration to an object and have it move. We apply forces, and the forces cause a change in the kinetic energy of the object.They will accelerate, of course, but the acceleration will depend on the inertia of the object. The inertia acts to resist the acceleration; with higher inertia, there is less acceleration for the same force.
To model this in a game, we could use the object's mass for the linear inertia and the moment of inertia (or inertia tensor in three dimension) for angular acceleration.
We could continue to extend the character data to keep track of these value and use a more complex update procedure to calculate the new velocities and positions. This is the method used by physics engines: the AI controls the motion of a character by applying forces to it. These forces represent the ways in which the character can affect its motion. Although not common for human characters, this approach is almost universal for controlling cars in driving games: the drive force of the engine and the forces associated with the steering wheels are the only ways in which the AI can control the movement of the car
Because most well-established steering algorithms are defined with acceleration outputs, it is not common to use algorithms that work directly with forces. Usually, the movement controller considers the dynamics of the character in a post-processing step called actuation
Actuation takes as input a desired change in velocity, the kind that would be directly applied in a kinematic system. The actuator then calculates the combination of forces that it can apply to get as near as possible to the desired velocity change.
3.2 KINEMATIC MOVEMENT ALGORITHMS
Kinematic movement algorithms use static data (position and orientation, no velocities) and output a desired velocity. The output is often simply an on or off and a target direction, moving at full speed or being stationary. Kinematic algorithms do not use acceleration, although the abrupt changes in velocity might be smoothed over serval frames.
Many games simplify things even further and force the orientation of a character to be in the direction it is traveling. If the character is stationary, it faces either a pre-set direction or the last direction it was moving in. If its movement algorithm return a target velocity, then that is used to set its orientation:
def getNewOrientation(currentOrientation, velocity): # Make sure we have a velocity if velocity.length() > 0: # Calculate orientation using an arc tangent of # the velocity components return atan2(-static.x, static.z) # Otherwise use the current orientation else: return currentOrientation
3.2.1 Seek
A kinematic seek behavior takes as input the character's and its target's static data. It calculates the direction from the character to the target and request a velocity along this line. The orientation values are typically ignored, although we can use the getNewOrientation function above to face in the direction we are moving.
class KinematicSeek: # Holds the static data for the character and target character target # Holds the maximum speed the character can travel maxSpeed def getSteering(): # Create the structure for output steering = new KinemeticSteeringOutput() # Get the direction to the target steering.velocity = target.position - character.position # The velocity is along this direction, at full speed steering.velocity.normalize() steering.velocity *= maxSpeed # Face in the direction we want to move character.orientation = getNewOrientation(character.orientation, steering.velocity) # Output the steering steering.rotation = 0 return steering
Data Structure and Interface
struct KinematicSteeringOutput velocity rotation
Performance
The algorithm is O(1) in both time and memory
Flee
# Get the direction away from the target steering.velocity = character.position - target.position
Arriving
The algorithm above is intended for use by a chasing character; it will never reach its goal, but continues to seek. If the character is moving to a particular point in the game world, then this algorithm may cause problems. Because it always moves at full speed, it is likely to overshoot an exact spot and wiggle backward and forward on successive frames trying to get there. This characteristic wiggle looks unacceptable. We need to end stationary at the target spot
To avoid this problem we have two choices. We can just give the algorithm a large radius of satisfaction and have it be satisfied if it gets closer to its target than that. Alternatively, if we support a range of movement speeds, then wen could slow the character down as it reaches its target, making it less likely to overshoot.
The second approach can still cause the characteristic wiggle, so we benefit from blending both approaches. Having the character slow down allows us to use a much smaller radius of satisfaction without getting wiggle and without the character appearing to stop instantly
We can modify the seek algorithm to check if the character is within the radius. If so, it doesn't worry about outputting anything. If it is not, then it tries to reach its target in a fixed length of time. (We've used a quarter of second, which is a reasonable figure. You can tweak the value if you need to.) If this would mean moving faster than its maximum speed, then it moves at its maximum speed. The fixed time to target is a simple trick that makes character slow down as it reaches its target. At 1 unit of distance away it wants to travel at 4 units per second. At a quarter of a unit of distance away it wants to travel at 1 unit per second, and so on.The fixed length of time can be adjusted to get the right effect. Higher values give a more gentle deceleration, and lower values make the braking more abrupt.
class KinematicArrive: # Holds the static data for the character and target character target # Holds the maximum speed the character can travel maxSpeed # Holds the satisfaction radius radius # Holds the time to target constant timeToTarget = 0.25 def getSteering() # Create the structure for output steering = new KinematicSteeringOutput() # Get the direction to the target steering.velocity = target.position - character.position # Check if we're within radius if steering.velocity.length() < radius # We can return to steering request return None # We need to move to our target we'd like to # get there in timeToTarget seconds steering.velocity /= timeToTarget # If this is too fast, clip it to the max speed if steering.velocity.lengt() > maxSpeed steering.velocity.normalize() steering.velocity *= maxSpeed # Face in the direction we want to move character.orientation = getNewOrientation(character.orientation, steering.velocity) # Ouput the steering steering.rotation = 0 return steering
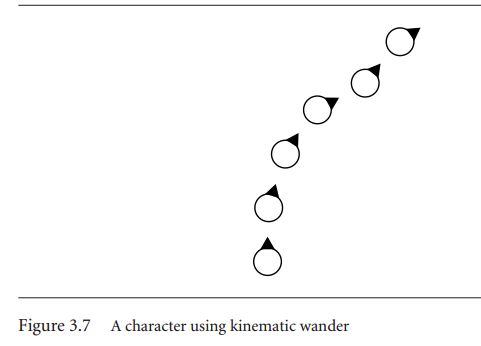
3.2.2 Wandering
A kinematic wander behavior always move in the direction of the character's current orientation with maximum speed. The steering behavior modifies the character's orientation, which allows the character to meander as it moves forward. The character is shown at successive frames. Note that it moves only forward at each frame(i.e., in the direction it was facing at the previous frame).
Pseudo-Code
class KinematicWander # Holds the static data for the character character # Holds the maximum speed the character can travel maxSpeed # Holds the maximum rotation speed we'd like, probaly # should be smaller than the maximum possible, to allow # a leisurely change in direction maxRotation def getSteering(): # Create the structure for output steering = new KinematicSteeringOutput() # Get velocity from the vector form of the orientation steering.velocity = maxSpeed * character.orientation.asVector() # Change our orientation randomly steering.rotation = randomBiomial() * maxRotation # Output the steering return steering
Data Structures
Orientation values have been given an asVector function that converts the orientation into a direction vector using the formulae given at the start of the chapter
Implementation Notes
We've used randomBinomial to generate the output rotation. This is a handy random number function that isn't common in the standard libraries of programming languages.It returns a random number between -1 and 1, where values around zero are more likely It can be simply created as:
def randomBinomial() return random() - random()
where random returns a random number from 0 to 1.
For our wander behavior, this means that the character is most likely to keep moving in its current direction. Rapid changes of direction are less likely, but still possible.
3.2.3 On the Website
3.3 STEERING BEHAVIORS
Steering behaviors extend the movement algorithm in the previous section by adding velocity and rotation. They are gaining larger acceptance in PC and console game development. In some genres(such as driving games) they are dominant in other genres they are only just beginning to see serious use.
There is a whole range of different steering behaviors, often with confusing and conflicting names. As the filed has developed, no clear naming schemes have emerged to tell the difference between one atomic steering behavior and a compound behavior combining serveral of them together.
In this book we'll separate the two: fundamental behaviors and behaviors that can be built up from combinations of these
There are a large number of named steering behaviors in various paper and code samples. Many of these are variations of one or two thems. Rather than catalog a zoo of suggested behaviors, we'll look at the basic structures common to many of them before looking at some exceptions with unusual features.
3.3.1 Steering Basics
By and large, most steering behaviors have a similar structure. They take as input the kinematic of the character that is moving and a limited amout of target infomation. The target information depends on the application. For chasing or evading behaviors, the target is often another moving character. Obstacle avoidance behaviors take a representation of the collision geometry of the world. It is also possible to specify a path as the target for a path following behavior.
The set of inputs to a steering behavior isn't always available in an AI-friendly format. Collision avoidance behaviors, in particular, need to have to access the collision information in the level. This can be an expensive process: checking the anticipated motion of the character using ray cast or trial movement through the level
Many steering behaviors operate on a group of targets. The famous flocking behavior, for example, relies on be able to move toward the average position of the flock. In these behaviors some processing is needed to summarize the set of targets into something that the behavior can react to. This may involve averaging properties of the whole set (to find and aim for their center of mass, for example), or it may involve ordering or searching among them (such as moving away from the nearest or avoiding bumping into those that are on a collision course)
Notice that the steering behavior isn't trying to do everything. There is no behavior to avoid obstacles while chasing a character and making detours via nearby power-ups. Each algorithm does a single thing and only takes the input needed to do that. To get more complicated behaviors, we will use algorithms to combine the steering behaviors and make them work together.
3.3.2 Variable Matching
The simplest family of steering behaviors operates by variable matching: they try to match one or more of the elements of the character's kinematic to a single target kinematic.
We might try to match the position of the target, for example, not caring about the other elements. This would involve accelerating toward the target position and decelerating once we are near. Alternatively, we could try to match the orientation of the target, rotating so that we align with it. We could even try to match the velocity of the target, following it on a parallel path and copying its movements buty staying a fixed distance way.
Variable matching behaviors take two kinematics as input: the character kinematic and the target kinematic. Different named steering behaviors try to match a different combination of elements, as well as adding aditional properties that control how the matching is performed. It is possible, but not particularly helpful, to create a general variable matching steering behavior and simply tell it which combination of elements to match. We've seen this type of implementation on acouple of occasions.
The problem arises when more than one element of the kinematic is being matched at the same time. They can easily conflic. We can match a target's position and orientation independently. But what about position and velocity? If we are matching their velocity, then wen can't be trying to get any closer.
A better technique is to have individual matching algorithms for each element and then combine them in the right combination later.This allows us to use any of the steering behavior combination techniques in this chapter, rather than having one hard-coded. The algorithm for combing steering behaviors are designed to resolve conflicts and so are perfect for this task.
For each matching steering behaviors, there is an opposite behavior that tries to get as far away from matching as possible. A behavior that tries to catch its target has an opposite that tries to avoid its target, and so on. As we saw in the kinematic seek behavior, the opposite form is usually a simple tweak to the basic behavior. We will look at several steering behaviors as paris along with theire opposite, rather than separting them into separte sections.
3.3.3 Seek and Flee
Seek tries to match the position of the character with the position of the target. Exactly as for the kinematic seek algorithm, it finds the direction to the target and heads toward it as fast as possible.Because the steering output is now an acceleration, it will accelerate as much as possible.
Obviously, if it keeps on accelerating, its speed will grow larger and larger. Most characters have a maximum speed they can travel; they can't accelerate indefinitely. The maximum can be explict, held in a variable or constant. The current speed of the character (the length of the velocity vector) is then checked regularly, and it is trimmed back if it exceeds the maximum speed. This is normally done as a post-processing step of the update function. It is not performed in a steering behavior. For example,
struct Kinematic: ... Member data as before ... def update(steering, maxSpeed, time): # Update the position and orientation position += velocity * time orientation += rotation * time # and the velocity and rotation velocity += steering.linear * time orientation += steering.angular * time # Check for speeding and clip if velocity.lengt() > maxSpeed: velocity.normalize() velocity *= maxSpeed
Alternatively, maximum speed might be a result of applying a drag to slow down the character a little at each frame. Games that rely on physics engines typicaly include drag. They do not need to check and clip the current velocity; the drag(applied in the udpate function) automatically limits the top speed.
Drag also helps another problem with this algorithm. Because the acceleration is always directed toward the target, if the target is moving, the seek behavior will end up orbiting rather than moving directly toward it. If there is drag in the system, then the orbit will become an inward spiral. If drag is sufficiently large, the player will not notice the spiral and will see the character simply move directly to its target.
Pseudo-Code
class Seek: # Holds the kinematic data for the character and target character target # Holds the maximum acceleration of the character maxAcceleration # Returns the desired steering output def getSteering(): # Create the structure to hold our output steering = new SteeringOutput() # Get the direction to the target steering.linear = target.position - character.position # Give full acceleration along this direction steering.linear.normalize() steering.linear *= maxAcceleration # Output the steering steering.angular = 0 return steering
Not that we've removed the change in orientation that was included in the kinematic version. We can simply set the orientation, as we did before, but a more flexible approach is to use variable matching to make the character face in the correct direction. The align behaviors, described below, give us the tools to change orientation using angular acceleration. The "look where you're going" behavior uses this to face the direction of movement
Data Structures and Interfaces
This class uses the SteeringOutput structure we defined earlier in the chapter. It holds linear and angular acceleration outputs.
Performance
The algorithm is again O(1) in both time and memory
Flee
Flee is the opposite of seek. It tries to get as far from the target possible. Just as for kinematic flee. The character will now move in the opposite direction of the target, accelerating as fast as possible.
# Get the direction to the target
steering.linear = character.position - target.position
3.3.4 Arrive
Seek will always move toward its goal with the greatest possible acceleration. This is fine if the target is constantly moving and the character needs to give chase at full speed. If the character arrives at the target, it will overshoot, reverse, and oscillate through the target, or it will more likely orbit around the target without getting closer
If the character is supposed to arrive at the target, it needs to slow down so that it arrives exactly at the right location, just as we saw in the kinematic arrive algorithm. Figure 3.9 shows the behavior of each for a fixed target. The trails show the paths taken by seek and arrive. Arrive goes straight to its target, while seek orbits a bit and ends up oscillating. The oscillation is not as bad for dynamic seek as it was in kinematic seek: the character cannot change direction immediately, so it appears to wobble rather than shake around the target.
The dynamic arrive behavior is a little more complex than then kinematic version. It uses two radii. The arrival radius, as before, lets the character get enough to the target without letting small errors keep it in motion. A second radius is also given, but is much larger. The incoming character will begin to slow down when it passes this radius. The algorithm calculates an ideal speed for the character. At the slowing-down radius, this is equal to its maximum speed. At the target point, it is zero (we want to have zero speed when we arrive). In between, the desired speed is an interpolated intermediate value, controlled by the distance from the target
The direction toward the target is calculated as before. This is then combined with the desired speed to give a target velocity. The algorithm looks at the current velocity of the character and works out the acceleration needed to turn it into the target velocity. We can't immediately change velocity, however, so the acceleration is calculated based on reaching the target velocity in a fixed time scale.
This is exactly the same process as for kinematic arrive, where we tried to get the character to arrive at its target in a quarter of a second. The fixed time period for dynamci arrive can usually be a little smaller; we'll use 0.1 as a good starting point.
When a character is moving too fast to arrive the right time, its target velocity will be smaller than its actual velocity, so the acceleration is in the opposite direction----it is acting to slow the character down.
Pseudo-Code
class Arrive: # Holds the kinematic data for the character and target character target # Holds the max acceleration and speed of the character maxAcceleration maxSpeed # Holds the radius for arriving at the target targetRadius # Holds the radius for beginning to slow down slowRadius # Holds the time over which to achieve target speed timeToTarget = 0.1 def getSteering(target): # Create the structure to hold our output steering = new SteeringOutput() # Get the direction to the target direction = target.position - character.position distance = direction.length() # Check if we are there, return no steering if distance < targetRadius return None # If we are outside the slowRaiuds, then go max speed if distance > slowRdius targetSpeed = maxSpeed # Otherwise calculate a scaled speed else: targetSpeed = maxSpeed * distance / slowRadius # The target velocity combines speed and direction targetVelocity = direction targetVelocity.normalize() targetVelocity *= targetSpeed # Acceleration tries to get to the target velocity steering.linear = targetVelocity - character.velocity steering.linear /= timeToTarget # Check if the accleration is too fast if steering.linear.length() > maxAcceleration steering.linear.normalize() steering.linear *= maxAcceleration # Output the steering steering.angular = 0 return steering
Performance
The algorithm is O(1) in both time and memory, as before
Implementation Notes
Many implementations do not use a target radius. Because the character will slow down to reach its target, there isn't the same likelihood of oscillation that we saw in kinematic arrive. Removing the target radius usually makes no noticeable difference. It can be significant, however, with low frame rates or where characters have high maximum speeds and low acceleration. In general, it is good practice to give a margin of error around any target, to avoid annoying instabilites.
Leave
Conceptually, the opposite behavior of arrive is leave. There is no point in implementing it, however. If we need to leave a target, we are unlikely to want to accelerate with miniscule (possibly zero) acceleration first and then build up. We are more likely to accelerate as fast as possible. So for practical purposes the opposite of arrive is flee.
3.3.5 Align
3.3.6 Velocity Matching
3.3.7 Delegated Behaviors
3.3.8 Pursue and Evade
3.3.9 Face
3.3.10 Looking Where You're Going
3.3.11 Wander
3.3.12 Path Following
3.3.13 Separation
3.3.14 Collision Avoidance
3.3.15 Obstacle and Wall Avoidance
3.3.16 Summary
3.4 COMBINING STEERING BEHAVIORS
3.4.1 Blending and Arbitration
3.4.2 Weighted Blending
3.4.3 Priorities
3.4.4 Cooperative Arbitration
3.4.5 Steering Pipline
3.5 PREDICTING PHYSICS
3.5.1 Aiming and Shooting
3.5.2 Projectile Trajectory
3.5.3 The Firing Solution
3.5.4 Projectiles with Drag
3.5.5 Iterative Targeting
3.6 JUMPING
3.6.1 Jump Points
3.6.2 Landing Pads
3.6.3 Hole Fillers
3.7 COORDINATED MOVEMENT
3.7.1 Fixed Formations
3.7.2 Scalable Formations
3.7.3 Emergent Formations
3.7.4 Two-Level Formation Steering
3.7.5 Implementation
3.7.6 Extending to More than Two Levels
3.7.7 Slot Roles and Better Assignment
3.7.8 Slot Assignment
3.7.9 Dynamic Slot and Plays
3.7.10 Tactical Movement
3.8 MOTOR CONTROL
3.8.1 Output Filtering
3.8.2 Capability-Sensitive Steering
3.8.3 Common Actuation Properties
3.9 MOVEMENT IN THE THIRD DIMENSION
3.9.1 Rotation in Three Dimensions
3.9.2 Converting Steering Behaviors to Three Dimensions
3.9.3 Align
3.9.4 Align to Vector
3.9.5 Face
3.9.6 Look Where You're Going
3.9.7 Wander
3.9.8 Faking Rotation Axes
CHAPTER4 PATHFINDING
4.1 THE PATHFINDING GRAPH
4.1.1 Graphs
4.1.2 Weighted Graphs
4.1.3 Directed Weighted Graphs
4.1.4 Terminology
4.1.5 Representation
4.2 DIJKSTRA
4.2.1 The Problem
4.2.2 The Algorithm
4.2.3 Pseudo-Code
4.2.4 Data Structures and Interfaces
4.2.5 Performance of Dijkstra
4.2.6 Weaknesses
4.3 A*
4.3.1 The Problem
4.3.2 The Algorithm
4.3.3 Pseudo-Code
4.3.4 Data Structures and Interfaces
4.3.5 Implementation Notes
4.3.6 Algorithm Performance
4.3.7 Node Array A*
4.3.8 Choosing a Heuristic
4.4 WORLD REPRESENTATIONS
4.4.1 Tile Graphs
4.4.2 Dirichlet Domains
4.4.3 Points of Visibility
4.4.4 Navigation Meshes
4.4.5 Non-Translational Problems
4.4.6 Cost Functions
4.4.7 Path Smoothing
4.5 IMPROVING ON A*
4.6 HIERARCHIAL PATHFINDING
4.6.1 The Hierarcdhical Pathfinding Graph
4.6.2 Pathfinding on the Hierarchical Graph
4.6.3 Hierarchical Pathfinding on Exclusions
4.6.4 Strange Effects of Hierarchies on Pathfinding
4.6.5 Instanced Geometry
4.7 OTHER IDEAS IN PATHFINDING
4.7.1 Open Goal Pathfinding
4.7.2 Dynamic Pathfinding
4.7.3 Other Kinds of Information Reuse
4.7.4 Low Memory Algorithms
4.7.5 Interruptible Pathfinding
4.7.6 Pooling Planners
4.8 CONTINUOUS TIME PATHFINDING
4.8.1 The Problem
4.8.2 The Algorithm
4.8.3 Implementation Notes
4.8.4 Performance
4.8.5 Weaknesses
4.9 MOVEMENT PLANNING
4.9.1 Animations
4.9.2 Movement Planning
4.9.3 Example
4.9.4 Footfalls
CHAPTER5 DECISION MAKING
5.1 OVERVIEW OF DECISION MAKING
5.2 DECISION TREES
5.2.1 The Problem
5.2.2 The Algorithm
5.2.3 Pseudo-Code
5.2.4 On the Website
5.2.5 Knowledge Representation
5.2.6 Implementation Nodes
5.2.7 Performance of Decision Trees
5.2.8 Balancing the Tree
5.2.9 Beyond the Tree
5.2.10 Random Decision Trees
5.3 STATE MACHINES
5.3.1 The Problem
5.3.2 The Algorithm
5.3.3 Pseudo-Code
5.3.4 Data Structures and Interfaces
5.3.5 On the Website
5.3.6 Performance
5.3.7 Implementation Notes
5.3.8 Hard-Coded FSM
5.3.9 Hierachical State Machines
5.3.10 Combining Decision Trees and State Machines
5.4 BEHAVIOR TREES
5.4.1 Implementing Behavior Trees
5.4.2 Pseudo-Code
5.4.3 Decorators
5.4.4 Concurrency and Timing
5.4.5 Adding Data to Behavior Trees
5.4.6 Reusing Trees
5.4.7 Limitations of Behavior Trees
5.5 FUZZY LOGIC
5.5.1 A Warning
5.5.2 Introduction to Fuzzy Logic
5.5.3 Fuzzy Logic Decision Making
5.5.4 Fuzzy State Machines
5.6 MARKOV SYSTEMS
5.6.1 Markov Processes
5.6.2 Markov State Machine
5.7 GOAL-ORIENTED BEHAVIOR
5.7.1 Goal-Oriented Behavior
5.7.2 Simple Selection
5.7.3 Overall Utility
5.7.4 Timing
5.7.5 Overall Utility GOAP
5.7.6 GOAP with IDA*
5.7.7 Smelly GOB
5.8 RULE-BASED SYSTEMS
5.8.1 The Problem
5.8.2 The Algorithm
5.8.3 Pseudo-Code
5.8.4 Data Structures and Interfaces
5.8.5 Implementation Notes
5.8.6 Rule Arbitration
5.8.7 Unification
5.8.8 Rete
5.8.9 Extensions
5.8.10 Where Next
5.9 BLACKBOARD ARCHITECTURES
5.9.1 The Problem
5.9.2 The Algorithm
5.9.3 Pseudo-Code
5.9.4 Data Structures and Interfaces
5.9.5 Performance
5.9.6 Other Things Are Blackboard Systems
5.10 SCRIPTIING
5.10.1 Language Facilities
5.10.2 Embedding
5.10.3 Choosing a Language
5.10.4 A Language Selection
5.10.5 Rolling Your Own
5.10.6 Scripting Languages and Other AI
5.11 ACTION EXECUTION
5.11.1 Types of Action
5.11.2 The Algorithm
5.11.3 Psedu-Code
5.11.4 Data Structures and Interfaces
5.11.5 Implementation Notes
5.11.6 Performance
5.11.7 Putting It All Together
CHAPTER6 TACTICAL AND STRATEGIC AI
6.1 Waypoint Tactics
6.1.1 Tactical Locations
6.1.2 Using Tactical Locations
6.1.3 Generating the Tactical Properties of a Waypoint
6.1.4 Automatically Generating the Waypoints
6.1.5 The Condensation Algorithm
6.2 Tactical Analyses
6.2.1 Representing the Game Level
6.2.2 Simple Influence Maps
6.2.3 Terrain Analysis
6.2.4 Learning with Tactical Analyses
6.2.5 A Structure for Tactical Analyses
6.2.6 Map Flooding
6.2.7 Convolution Filters
6.2.8 Cellular Automata
6.3 Tactical Pathfinding
6.3.1 The Cost Function
6.3.2 Tactic Weights and Concern Blending
6.3.3 Modifying the Pathfinding Heuristic
6.3.4 Tactical Graphs for Pathfinding
6.3.5 Using Tactical Waypoints
6.4 Coordinated Action
6.4.1 Multi-Tier AI
6.4.2 Emergent Cooperation
6.4.3 Scripting Group Actions
6.4.4 Military Tactics
CHAPTER7 LEARNING
7.1 Learning Basics
7.1.1 Online or Offline Learning
7.1.2 Intra-Behavior Learning
7.1.3 Inter-Behavior Learning
7.1.4 A Warning
7.1.5 Over-Learning
7.1.6 The Zoo of Learning Algorithms
7.1.7 The Balance of Effort
7.2 Parameter Modification
7.2.1 The Parameter Landscape
7.2.2 Hill Climbing
7.2.3 Extensions to Basic Hill Climbing
7.2.4 Annealing
7.3 Action Prediction
7.3.1 Left or Right
7.3.2 Raw Probability
7.3.3 String Matching
7.3.4 N -Grams
7.3.5 Window Size
7.3.6 Hierarchical N -Grams
7.3.7 Application in Combat
7.4 Decision Learning
7.4.1 Structure of Decision Learning
7.4.2 What Should You Learn?
7.4.3 Four Techniques
7.5 Naive Bayes Classifiers
7.5.1 Implementation Notes
7.6 Decision Tree Learning
7.6.1 ID3
7.6.2 ID3 with Continuous Attributes
7.6.3 Incremental Decision Tree Learning
7.7 Reinforcement Learning
7.7.1 The Problem
7.7.2 The Algorithm
7.7.3 Pseudo-Code
7.7.4 Data Structures and Interfaces
7.7.5 Implementation Notes
7.7.6 Performance
7.7.7 Tailoring Parameters
7.7.8 Weaknesses and Realistic Applications
7.7.9 Other Ideas in Reinforcement Learning
7.8 Artificial Neural Networks
7.8.1 Overview
7.8.2 The Problem
7.8.3 The Algorithm
7.8.4 Pseudo-Code
7.8.5 Data Structures and Interfaces
7.8.6 Implementation Caveats
7.8.7 Performance
7.8.8 Other Approaches
CHAPTER8 BOARD GAMES
8.1 Game Theory
8.1.1 Types of Games
8.1.2 The Game Tree
8.2 Minimaxing
8.2.1 The Static Evaluation Function
8.2.2 Minimaxing
8.2.3 The Minimaxing Algorithm
8.2.4 Negamaxing
8.2.5 AB Pruning
8.2.6 The AB Search Window
8.2.7 Negascout
8.3 Transposition Tables and Memory
8.3.1 Hashing Game States
8.3.2 What to Store in the Table
8.3.3 Hash Table Implementation
8.3.4 Replacement Strategies
8.3.5 A Complete Transposition Table
8.3.6 Transposition Table Issues
8.3.7 Using Opponent’s Thinking Time
8.4 Memory-Enhanced Test Algorithms
8.4.1 Implementing Test
8.4.2 The MTD Algorithm
8.4.3 Pseudo-Code
8.5 Opening Books and Other Set Plays
8.5.1 Implementing an Opening Book
8.5.2 Learning for Opening Books
8.5.3 Set Play Books
8.6 Further Optimizations
8.6.1 Iterative Deepening
8.6.2 Variable Depth Approaches
8.7 Turn-Based Strategy Games
8.7.1 Impossible Tree Size
8.7.2 Real-Time AI in a Turn-Based Game
CHAPTER9 EXECUTION MANAGEMENT
9.1 Scheduling
9.1.1 The Scheduler
9.1.2 Interruptible Processes
9.1.3 Load-Balancing Scheduler
9.1.4 Hierarchical Scheduling
9.1.5 Priority Scheduling
9.2 Anytime Algorithms
9.3 Level of Detail
9.3.1 Graphics Level of Detail
9.3.2 AI LOD
9.3.3 Scheduling LOD
9.3.4 Behavioral LOD
9.3.5 Group LOD
9.3.6 In Summary
CHAPTER10 WORLD INTERFACING
10.1 Communication
10.2 Getting Knowledge Efficiently
10.2.1 Polling
10.2.2 Events
10.2.3 Determining What Approach to Use
10.3 Event Managers
10.3.1 Implementation
10.3.2 Event Casting
10.3.3 Inter-Agent Communication
10.4 Polling Stations
10.4.1 Pseudo-Code
10.4.2 Performance
10.4.3 Implementation Notes
10.4.4 Abstract Polling
10.5 Sense Management
10.5.1 Faking It
10.5.2 What Do We Know?
10.5.3 Sensory Modalities
10.5.4 Region Sense Manager
10.5.5 Finite Element Model Sense Manager
CHAPTER11 TOOLS AND CONTENT CREATION
11.0.1 Toolchains Limit AI
11.0.2 Where AI Knowledge Comes from
11.1 Knowledge for Pathfinding and Waypoint Tactics
11.1.1 Manually Creating Region Data
11.1.2 Automatic Graph Creation
11.1.3 Geometric Analysis
11.1.4 Data Mining
11.2 Knowledge for Movement
11.2.1 Obstacles
11.2.2 High-Level Staging
11.3 Knowledge for Decision Making
11.3.1 Object Types
11.3.2 Concrete Actions
11.4 The Toolchain
11.4.1 Data-Driven Editors
11.4.2 AI Design Tools
11.4.3 Remote Debugging
11.4.4 Plug-Ins
CHAPTER12 DESIGNING GAME AI
12.1 The Design
12.1.1 Example
12.1.2 Evaluating the Behavior
12.1.3 Selecting Techniques
12.1.4 The Scope of One Game
12.2 Shooters
12.2.1 Movement and Firing
12.2.2 Decision Making
12.2.3 Perception
12.2.4 Pathfinding and Tactical AI
12.2.5 Shooter-Like Games
12.3 Driving
12.3.1 Movemen
12.3.2 Pathfinding and Tactical AI
12.3.3 Driving-Like Games
12.4 Real-Time Strategy
12.4.1 Pathfinding
12.4.2 Group Movement
12.4.3 Tactical and Strategic AI
12.4.4 Decision Making
12.5 Sports
12.5.1 Physics Prediction
12.5.2 Playbooks and Content Creation
12.6 Turn-Based Strategy Games
12.6.1 Timing
12.6.2 Helping the Player
CHAPTER13 AI-BASED GAME GENRES
13.1 Teaching Characters
13.1.1 Representing Actions
13.1.2 Representing the World
13.1.3 Learning Mechanism
13.1.4 Predictable Mental Models and Pathological States
13.2 Flocking and Herding Games
13.2.1 Making the Creatures
13.2.2 Tuning Steering for Interactivity
13.2.3 Steering Behavior Stability
13.2.4 Ecosystem Design
References
References
A.1 Books, Periodicals, and Papers
Abelson, H., & Sussman, G. J. (1996). Structure and interpretation of computer programs (2nd ed.).Cambridge, MA: MIT Press.
Buckley, J. J., & Eslami, E. (2002). An introduction to fuzzy logic and fuzzy sets. Berlin/New York:Springer-Verlag.
Eberly, D. (2003). Conversion of left-handed coordinates to right-handed coordinates.
Eberly, D. (2004). Game Physics. San Francisco: Morgan Kaufmann.
Ericson, C. (2005). Real-time collision detection. San Francisco: Morgan Kaufmann.
Giarratano, J. C., & Ricley, G. D. (1998). Expert systems: Principles and programming (3rd ed.).Florence, KY: Course Technology.
Gonzalez, R. C., & Woods, R. E. (2002). Digital image processing (2nd ed.). New York: Prentice Hall.
Ierusalimschy, R. (2006). Programming in Lua (2nd ed.). Published by lua.org.
Kourkolis,M. (Ed.), (1986). APP-6 Military symbols for land-based systems. NATO Military Agency for Standardization (MAS).
McCulloch,W. S., & Pitts,W. (1943). A logical calculus of the ideas immanent in nervous activity.Bulletin of Mathematical Biophysics, 5:115–133.
Millington, I. (2007). Game physics engine development. San Francisco: Morgan Kaufmann.
Newell, A., & Simon, H. A. (1976). Computer science as empirical inquiry: Symbols and search. Communications of the Association for Computing Machinery, 19:111–126.
Pilone, D., & Pitman, N. (2005). UML 2 in a Nutshell. Sebastopol, CA: O’Reilly Media, Inc.
Russell, S., & Norvig, P. (2002). Artificial intelligence: A modern approach (2nd ed.). Upper Saddle River, NJ: Prentice Hall.
Schneider, P. J., & Eberly, D. (2003). Geometric tools for computer graphics. San Mateo, CA: Morgan Kaufmann.
Turing, A. M. (1950). Computing machinery and intelligence. Mind, 59:433–460.
U.S. Army Infantry School. (Ed.), (1992). FM 7-8 Infantry rifle platoon and squad. Washington DC: Department of the Army.
U.S. Army Infantry School. (Ed.), (2002). FM 3-06.11 Combined arms operation in urban terrain. Washington DC: Department of the Army.
van den Bergen, G. (2003). Collision detection in interactive 3D environments. San Mateo, CA: Morgan Kaufmann.
Waltz, F. M., & Miller, J. W. V. (1998). An efficient algorithm for Gaussian blur using finite-state machines. In: Proceedings of the SPIE Conference on Machine Vision Systems for Inspection and Metrology VII.
Wolpert, D. H., & Macready, W. G. (1997). No free lunch theorems for optimization. IEEE Transactions on Evolutionary Computation, 1(1):67–82.
A.2 Games
This section gives more comprehensive information on the games mentioned in the book. Games
are provided with their developer and publisher, the platforms on which the game was published,
and its year of release. They are ordered by developer name, after the citation style used throughout
the book.
Developers tend to change their names often, so this list uses the developer’s name as it was
when the game was developed. Many games are released on one or two platforms initially and
then later ported to other platforms. This list indicates the original platform or platforms for
a game’s release. Where the game was released for more than two platforms, it is indicated as
“Multiple platforms.”
2015, Inc. (2002). Medal of Honor: Allied Assault. Electronic Arts. [PC].
Activision Publishing, Inc. (1993). Alien vs. Predator. Activision Publishing, Inc. [SNES].
Atari. (1980). 3D Tic-Tac-Toe. Sears, Roebuck and Co. [Atari 2600].
Bioware Corporation. (2002). Neverwinter Nights. Infogrames, Inc. [PC].
Bizarre Creations. (1996). Formula 1. Psygnosis. [PlayStation and PC].
Blade Interactive. (2004). World Championship Pool 2004. Jaleco Entertainment. [PC].
Blizzard Entertainment. (1994). Warcraft: Orcs and Humans. Blizzard Entertainment. [PC].
Blizzard Entertainment. (2002). Warcraft 3: Reign of Chaos. Blizzard Entertainment. [PC].
Bullfrog Productions Ltd. (1997). Dungeon Keeper. Electronic Arts, Inc. [PC].
Bungie Software. (2001). Halo. Microsoft Game Studios. [Xbox].
Bungie Software. (2004). Halo 2. Microsoft Game Studios. [Xbox].
Bungie Software. (2007). Halo 3. Microsoft Game Studios. [Xbox 360].
Cavedog Entertainment. (1997). Total Annihilation. GT Interactive Software Europe Ltd. [PC].
Core Design Ltd. (1996). Tomb Raider. Eidos Interactive, Inc. [Multiple platforms].
Core Design Ltd. (1998). Tomb Raider III: The Adventures of Lara Croft. Eidos Interactive, Inc.[Multiple platforms].
Core Design Ltd. (2002). Herdy Gerdy. Eidos Interactive Ltd. [PlayStation 2].
Criterion Software. (2001). Burnout. Acclaim Entertainment. [Multiple platforms].
Cryo Interactive Entertainment. (1992). Dune. Virgin Interactive Entertainment. [Multiple platforms].
Crytek. (2004). FarCry. Ubisoft. [PC].
Cyberlife Technology Ltd. (1997). Creatures. Mindscape Entertainment. [PC].
DMA Design. (2001). Grand Theft Auto 3. Rockstar Games. [PlayStation 2].
Dynamix. (2001). Tribes II. Sierra On-Line. [PC].
Electronic Arts Canada. (2000). SSX. Electronic Arts. [PlayStation 2].
Electronic Arts Los Angeles. (2007). Medal of Honor: Airborne. Electronic Arts. [Multiple platforms].
Electronic Arts Tiburon. (2008). Madden NFL 2009. Electronic Arts. [Multiple platforms].
Elixir Studios. (2003). Republic: The Revolution. Eidos, Inc. [PC].
Elixir Studios. (2004). Evil Genius. Sierra Entertainment, Inc. [PC].
Epic Games. (1998). Unreal. GT Interactive. [PC].
Firaxis Games. (2001). Sid Meier’s Civilization III. Infogrames. [PC].
Firaxis Games. (2005). Sid Meier’s Civilization IV. 2K Games. [PC].
id Software. (1992). Wolfenstein 3D. Activision, Apogee, and GT Interactive. [PC].
id Software. (1993). Doom. id Software. [PC].
id Software. (1997). Quake. Activision, Inc. [PC].
id Software. (2004). Doom 3. Activision. [PC].
Incog, Inc., Entertainment. (2003). Downhill Domination. SCEA. [PlayStation 2].
Ion Storm. (2000). Deus Ex. Eidos Interactive. [PC].
Konami Corporation. (1998). Metal Gear Solid. Konami Corporation. [PlayStation].
K-D Lab Game Development. (2004). Perimeter. 1C. [PC].
Lionhead Studios Ltd. (2001). Black and White. Electronic Arts, Inc. [PC].
Looking Glass Studios, Inc. (1998). Thief: The Dark Project. Eidos, Inc. [PC].
LucasArts Entertainment Company LLC. (1999). Star Wars: Episode 1—Racer. LucasArts Entertainment Company LLC. [Multiple Platforms].
Manic Media Productions. (1995). Manic Karts. Virgin Interactive Entertainment. [PC].
Maxis. (1989). SimCity. Maxis. [PC].
Maxis Software, Inc. (2000). The Sims. Electronic Arts, Inc. [PC].
Midway Games West, Inc. (1979). Pac-Man. Midway Games West, Inc. [Arcade].
Mindscape. (1998). Warhammer: Dark Omen. Electronic Arts. [PC and PlayStation].
Monolith Productions, Inc. (2002). No One Lives Forever 2. Sierra. [PC].
Monolith Productions, Inc. (2005). F.E.A.R. Vivendi Universal Games. [PC].
Monolith Productions, Inc. (2009). F.E.A.R. 2: Project Origin Warner Bros. Interactive Entertainment, In. [PC].
Naughty Dog, Inc. (2001). Jak and Daxter: The Precursor Legacy. SCEE Ltd. [PlayStation 2].
Nintendo Entertainment, Analysis and Development. (2001). Pikmin. Nintendo Co. Ltd. [GameCube].
Nintendo Entertainment, Analysis and Development. (2002). Super Mario Sunshine. Nintendo Co. Ltd. [GameCube].
Nintendo Entertainment, Analysis and Development. (2004). Pikmin 2. Nintendo Co. Ltd. [GameCube].
Oddworld Inhabitants, Inc. (1997). Oddworld: Munch’s Oddysee. Microsoft Game Studios. [PlayStation and PC].
Pandemic Studios. (2004). Full Spectrum Warrior. THQ. [PC and Xbox].
Pivotal Games Ltd. (2002). Conflict: Desert Storm. SCi Games Ltd. [Multiple Platforms].
Polyphony Digital. (1997). Gran Turismo. SCEI. [PlayStation].
Psygnosis. (1995). Wipeout. SCEE. [PlayStation].
Quicksilver Software, Inc. (2003). Master of Orion 3. Infogrames. [PC].
Radical Entertainment. (2005). Scarface. Vivendi Universal Games. [Multiple platforms].
Rare Ltd. (1997). Goldeneye 007. Nintendo Europe GmbH. [Nintendo 64].
Raven Software. (2002). Soldier of Fortune 2: Double Helix. Activision. [PC and Xbox].
Rebellion. (1994). Alien vs. Predator. Atari Corporation. [Jaguar].
Rebellion. (2005). Sniper Elite. Namco. [Multiple platforms].
Rebellion. Cyberspace. [Nintendo Game Boy].
Red Storm Entertainment, Inc. (2001). Tom Clancy’s Ghost Recon. Ubisoft Entertainment Software. [PC].
Reflections Interactive. (1999). Driver. GT Interactive. [PlayStation and PC].
Relic Entertainment. (1999). Homeworld. Sierra On-Line. [PC].
Relic Entertainment. (2006). Company of Heroes. THQ Inc. [PC].
Revolution Software Ltd. (1994). Beneath a Steel Sky. Virgin Interactive, Inc. [PC].
SEGA Entertainment, Inc. (1987). Golden Axe. SEGA Entertainment, Inc. [Arcade].
Sick Puppies Studio and International Hobo Ltd. (2003). Ghost Master. Empire Interactive Entertainment. [PC].
Sony Computer Entertainment. (2002). Otostaz. Sony Computer Entertainment. [PlayStation 2]. (Japanese release only).
Strategic Simulations, Inc. (1980). Computer Bismark. Strategic Simulations, Inc. [Apple].
Team 17. (2003). Worms 3D. Sega Europe Ltd. [Multiple platforms].
TechnoSoft. (1989). Herzog Zwei. TechnoSoft. [Sega Genesis].
The Creative Assembly Ltd. (2004). Rome: Total War. Activision Publishing, Inc. [PC].
The Creative Assembly Ltd. (2009). Empire: Total War. SEGA of America, Inc. [PC].
TimeGate Studios. (2001). Kohan: Ahriman’s Gift. Strategy First. [PC].
Turn 10 Studios. (2005). Forza Motorsport. Microsoft Game Studios. [Xbox].
Ubisoft Montpellier Studios. (2003). Beyond Good and Evil. Ubisoft Entertainment. [Multiple platforms].
Ubisoft Montreal Studios. (2002). Splinter Cell. Ubisoft Entertainment Software. [Multiple platforms].
Ubisoft Montreal Studios. (2008). Far Cry 2. Ubisoft Entertainment Software. [Multiple platforms].
Valve. (1998). Half-Life. Sierra On-Line. [PC].
Valve. (2004). Half-Life 2. [PC].
Warthog Games. (2003). Mace Griffin: Bounty Hunter. Vivendi Universal Games. [Multiple platforms].
Westwood Studios. (1992). Dune II. Virgin Interactive Entertainment. [PC].
Westwood Studios. (1995). Command and Conquer. Virgin Interactive Entertainment. [PC].
Zipper Interactive. (2002). SOCOM: U.S. Navy SEALs. SCEA. [PlayStation 2].