【备战NOIP】专题复习1-动态规划-背包问题

【备战NOIP】专题复习1-动态规划-背包问题

在阅读本文之前，建议先阅读背包九讲。本文通过相关的题目来讨论一些常见的背包套路，其中包括，01背包的模板以及应用，完全背包的模板以及应用，多重背包的模板以及应用，分组背包的模板以及应用，简单的依赖背包的模板，以及二维费用背包模板，背包第K优解。最后给出了一些习题和解析。

01背包模板

题目链接：采药

题意：给出$n$个物品和背包体积容量$m$，第$i$个物品体积的花费是$c[i]$，价值是$w[i]$，每个物品最多只能取一次，求取一些物品，在不超过容量$m$的情况下能得到的最大价值。

解析：这是$01$背包的模板题，就不多说了，如下的状态转移方程是所有背包的基础，$dp[j]=max(dp[j],dp[j-c[i]]+w[i])$，对应着取或不取第$i$件物品的最优值。代码具体实现如下：

拓展：如果题目问的是恰好装满背包，只需要初始化$dp[i]=-inf,dp[0]=0$即可

#include
using namespace std;
const int N=105;
int n,c[N],w[N],m,dp[1005]; 
int main()
{
    cin>>m>>n;
    for(int i=1;i<=n;i++) cin>>c[i]>>w[i];
    for(int i=1;i<=n;i++)
   		for(int j=m;j>=c[i];j--)
   			dp[j]=max(dp[j],dp[j-c[i]]+w[i]);
	cout<

01背包的应用

题目链接：装箱问题

题意：给出$n$个物品和容量$m$，第$i$个物品体积的花费是$c[i]$，求取一些物品，求在不超过容量$m$的情况下最小的剩余容量。

解析：对比于$01$背包模板题，物品少了价值这个属性，所以很容易想到，对于第$i$个物品，令$w[i]=c[i]$，即可转化为$01$背包模板题，可求出最大的价值$dp[m]$，最后$m-dp[m]$便是答案。代码如下：

#include
using namespace std;
const int N=105;
int n,c[N],w[N],m,dp[20005]; 
int main()
{
    cin>>m>>n;
    for(int i=1;i<=n;i++) cin>>c[i],w[i]=c[i];
    for(int i=1;i<=n;i++)
   		for(int j=m;j>=c[i];j--)
   			dp[j]=max(dp[j],dp[j-c[i]]+w[i]);
	cout<

题目链接： 最大约数和

题意：选取和不超过 $s$ 的若干个不同的正整数，使得所有数的约数（不含它本身）之和最大。

解析：将问题看成是有$s$个物品，背包的体积容量是$s$，第$i$个物品的体积的花费是$i$，价值是其约数之和。在不超过容量$s$的情况下能得到的最大价值。代码如下：

#include
using namespace std;
const int N=1005;
int n,c[N],w[N],m,dp[1005]; 
int f(int x)
{
	int ans=0;
	for(int i=1;i>m;
    n=m;
    for(int i=1;i<=n;i++) c[i]=i,w[i]=f(i);
    for(int i=1;i<=n;i++)
   		for(int j=m;j>=c[i];j--)
   			dp[j]=max(dp[j],dp[j-c[i]]+w[i]);
	cout<

完全背包模板

题目链接： 疯狂的采药

题意：给出$n$个物品和背包体积容量$m$，第$i$个物品体积的花费是$c[i]$，价值是$w[i]$，每个物品可以取无数次，求取一些物品，在不超过容量$m$的情况下能得到的最大价值。

解析：设$dp[i][j]$为前$i$个物品在背包容量限制为$j$的情况下能获取到的最大价值，接下来分类讨论，如果不取第$i$个物品，则问题转化为前$i-1$个物品在背包容量限制为$j$的情况下能获取到的最大价值，即$dp[i-1][j]$，如果取了第$i$个物品，由于第$i$个物品可以取多次，问题还是转化为前$i$个物品在背包容量限制为$j-c[i]$的情况下能获取到的最大价值,即$dp[i][j-c[i]]+w[i]$。故有$dp[i][j]=max(dp[i-1][j],dp[i][j-c[i]]+w[i])$，优化一维数组空间后有$dp[j]=max(dp[j],dp[j-c[i]]+w[i])$，且从小到大更新即可。代码如下：

#include
using namespace std;
typedef long long ll;
const int N=1e4+5;
int n,c[N],w[N],m;
long long dp[int(1e7+5)]; 
int main()
{
    cin>>m>>n;
    for(int i=1;i<=n;i++) cin>>c[i]>>w[i];
    for(int i=1;i<=n;i++)
   		for(int j=c[i];j<=m;j++)
   			dp[j]=max(dp[j],dp[j-c[i]]+w[i]);
	cout<

完全背包的应用

题目链接： 货币系统

题意：给出$n$个数字，求有多少个数字不能被其它数字表示，例如$3,19,10,6 $中$3$和$10$不能被其它数字表示出来，故而输出$2$。

解析：由于每个数字可以使用多次，所以考虑类似完全背包的做法，令$dp[i][j]$为前$i$个数字能表示出$j$的方案数，那么显然有$dp[i][j]=dp[i-1][j]+dp[i][j-a[i]]$，同样可以优化一维，所以有$dp[j]=dp[j]+dp[j-a[i]]$,那么可以先预处理出$dp[j],0<=j<=Max$,然后满足$dp[a[i]]==1$的数字$a[i]$不能被其它数字表示出来，因为只有被它本身表示出来这$1$种方案。统计有有多少个这样的$a[i]$即可。初始化为$dp[0]=0$即可，代码如下：

拓展：如果题目问的是至少有多少个数字可以拼出某个数，一样可以使用类似的状态转移方程，$dp[j]=min(dp[j],dp[j-a[i]]+1)$，并初始化$dp[i]=inf,1<=i<=V,dp[0]=0$

#include
using namespace std;
const int N=30005;
int a[N],n,t,dp[N];
int main()
{
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d",&n);
		int Max=0;
		for(int i=1;i<=n;i++) scanf("%d",&a[i]),Max=max(Max,a[i]);
		memset(dp,0,sizeof(dp));
		dp[0]=1;
		for(int i=1;i<=n;i++)
		{
			for(int j=a[i];j<=Max;j++)
				dp[j]+=dp[j-a[i]];
		}
		int ans=0;
		for(int i=1;i<=n;i++) 
			if(dp[a[i]]==1) ans++;
		cout<

多重背包

题目链接： 宝物筛选

题意：给出$n$个物品和最大载重为$W$的车，第$i$个物品重量是$w[i]$，价值是$v[i]$，每个物品最多取$m[i]$件，求取一些物品，在载重不超过$W$的情况下能得到的最大价值。

解析：考虑将问题转化为$01$背包或完全背包处理，对于第$i$个物品，如果有$w[i]\ast m[i]>=W$，则可以任务第$i$件物品可以取无限多件，否则，对于$m[i]$，需要将其拆分成若干组物品，且必须满足一个条件，就是$0,1,2,...,m[i]$这些件数需要由这若干组取或不取表示出来，最简单的方法是分成$m[i]$组，每组$1$件，这样必然可以做到$0,1,2,...,m[i]$这些件数需要由这若干组取或不取表示出来，但是这样最终的物品件数太多，复杂度太高，需要优化，这里采取二进制优化的方法，即每一组的件数为$2^0,2^1,2^2,2^3,...,2^k,m[i]-{\sum }_{j=0}^k(2^j)$,这样就可以用$log(m[i])$组表示出$0,1,2,...,m[i]$的每一个数字。例如要表示出$100$以内的任何一个数字，完全可以用$1,2,4,8,16,32,37$这$7$个数组取或不取表示出来。接着，把每一组看成是一件物品，就转化$01$背包问题了。代码如下：

#include
using namespace std;
const int N=1e5+5;
int n,V;
struct node
{
	int v,w,c;
	node(int v=0,int w=0,int c=0):v(v),w(w),c(c){}
}a[N];
int dp[N];
void complete_backpack(int v,int w)
{
	for(int j=v;j<=V;j++) dp[j]=max(dp[j],dp[j-v]+w);
}
void onezero_backpack(int v,int w)
{
	for(int j=V;j>=v;j--) dp[j]=max(dp[j],dp[j-v]+w);
}
void multi_backpack(int v,int w,int c)
{
	if(c*v>=V) complete_backpack(v,w);
	else
	{
		for(int k=1;k<=c;k<<=1) onezero_backpack(k*v,k*w),c-=k;
		onezero_backpack(c*v,c*w);
	}
}
int main()
{
	cin>>n>>V;
	for(int i=1;i<=n;i++) cin>>a[i].w>>a[i].v>>a[i].c;
	for(int i=1;i<=n;i++) multi_backpack(a[i].v,a[i].w,a[i].c);
	cout<

分组背包

题目链接：通天之分组背包

题意：$n$件物品，分成$k$组，每组最多只能取$1$件，问在不超过容量的情况下能获取的最大价值。

解析：定义$dp[i][j]$为前$i$组在容量限制为$j$的情况下能获取的最优解。要么第$i$组不取，对应的是$dp[i-1][j]$，要么第$i$组中取第$k$个数，对应的是$dp[i-1][j-v[i][k]]+w[i][k]$,压缩一维后$dp[j]=max(dp[j],dp[j-v[i][k]]+w[i][k])$，倒序更新即可。代码如下：

拓展：如果每组限制最多取$p$件呢？多开一维即可。$dp[q][j]=max(dp[q][j],dp[q-1][j-v[i][k]]+w[i][k])$

#include
using namespace std;
const int N=1005;
struct node
{
	int v,w;
	node(int v,int w):v(v),w(w){
	}
};
vectorg[N];
int n,V,dp[N];
int main()
{
	cin>>V>>n;
	int kk=0;
	for(int i=1;i<=n;i++)
	{
		int a,b,c;
		cin>>a>>b>>c;
		kk=max(kk,c);
		g[c].push_back(node(a,b));
	}
	for(int i=1;i<=kk;i++)
		for(int j=V;j>=0;j--)
		{
			for(int k=0;k=0)
					dp[j]=max(dp[j],dp[j-g[i][k].v]+g[i][k].w);
//				printf("dp[%d]=%d\n",j,dp[j]);
			}
		}
	cout<

简单的依赖背包

题目链接：金明的预算方案

题意：$n$件物品，有些物品是主件，有些是附件，取附件必须先取主件，每个主件最多有2个附件，问在不超过容量的情况下能获取的最大价值。

解析：分成五类讨论即可。

1. 不选，然后去考虑下一个
2. 选且只选这个主件
3. 选这个主件，并且选附件1
4. 选这个主件，并且选附件2
5. 选这个主件，并且选附件1和附件2.

代码如下：

#include
using namespace std;
const int N=40005;
struct node
{
	int v,w,q;
	node(int v=0,int w=0,int q=0):v(v),w(w),q(q){}
}a[N];
vectorG[N];
int n,V,dp[N];
int main()
{
	cin>>V>>n;
	for(int i=1;i<=n;i++)
	{
		int v,w,q;
		cin>>v>>w>>q;
		a[i]=node(v,w,q);
		if(q) G[q].push_back(i);
	}
	for(int i=1;i<=n;i++)
	{
		if(a[i].q==0)
		{
			for(int j=V;j>=0;j--)
			{
				int v=a[i].v,w=a[i].w;
				if(j>=v) dp[j]=max(dp[j],dp[j-v]+w*v);
				if(G[i].size()>=1)
				{
					int v1=a[G[i][0]].v,w1=a[G[i][0]].w;
					if(j>=(v+v1))
						dp[j]=max(dp[j],dp[j-(v+v1)]+w*v+w1*v1);
				}
				if(G[i].size()>=2)
				{
					int v1=a[G[i][0]].v,w1=a[G[i][0]].w;
					int v2=a[G[i][1]].v,w2=a[G[i][1]].w;
					if(j>=(v+v2))
						dp[j]=max(dp[j],dp[j-(v+v2)]+w*v+w2*v2);
					if(j>=(v+v1+v2))
						dp[j]=max(dp[j],dp[j-(v+v1+v2)]+w*v+w1*v1+w2*v2);
				}
			}
		}
	}
	cout<

二维费用背包

题目链接：NASA的食物计划

题意：给出$n$个物品和花费限制$C1$和$C2$，第$i$个物品有两个花费，分别是$c1[i]$和$c2[i]$，价值是$w[i]$，每个物品最多只能取一次，求取一些物品，在不超过花费限制$C1$和$C2$的情况下能得到的最大价值。

解析：再开一维即可，$dp[j][k]=max(dp[j][k],dp[j-c1[i]][c2[i]]+w[i])$，代码如下：

#include
using namespace std;
typedef long long ll;
const int N=1e3+5,inf=0x3f3f3f3f;
int dp[N][N],n,c1[N],c2[N],w[N],C1,C2;
int main()
{
	cin>>C1>>C2>>n;
	for(int i=1;i<=n;i++) cin>>c1[i]>>c2[i]>>w[i];
	for(int i=1;i<=n;i++)
		for(int j=C1;j>=c1[i];j--)
			for(int k=C2;k>=c2[i];k--)
				dp[j][k]=max(dp[j][k],dp[j-c1[i]][k-c2[i]]+w[i]);
	cout<

背包第K优解

题目链接：多人背包

题意：求$01$背包前$k$优解的价值和。

解析：显然要维护背包的前$k$优解，考虑到$01$背包的状态转移方程$dp[j]=max(dp[j],dp[j-c[i]]+w[i])$，最优解$dp[j][1]$显然是取$dp[j][1]$和$dp[j-c[i]][1]+w[i]$的最大值,$dp[j][2]$显然是取$dp[j][1]$和$dp[j-c[i]][1]+w[i]$$dp[j][2]$和$dp[j-c[i]][2]+w[i]$4个值中的次大值，同理可以维护出$dp[j][k]$,由于$dp[j][k]$和$dp[j-c[i]][k]+w[i]$都是有序序列，故可以做到线性的复杂度取两个序列的前$k$大，注意合并的过程中要用临时数组暂存。代码如下：

#include
using namespace std;
const int N=5005;
long long k,v,n;
long long c[N],w[N];
long long dp[5005][55];
long long tmp[N];
int main()
{
	cin>>k>>v>>n;
	for(int i=1;i<=n;i++) cin>>c[i]>>w[i];
	for(int j=0;j<=v;j++)
		for(int p=0;p<=k;p++) dp[j][p]=-0x3f3f3f3f;
//	cout<=c[i];j--)
		{
			int p1=1,p2=1,p=1;
			while(p<=k)
			{
				if(dp[j][p1]>dp[j-c[i]][p2]+w[i]) tmp[p++]=dp[j][p1++];
				else tmp[p++]=dp[j-c[i]][p2++]+w[i];
			}
//			printf("p1=%d,p2=%d\n",p1,p2);
			for(int p=1;p<=k;p++) dp[j][p]=tmp[p];
//			for(int p=1;p<=k;p++) printf("dp[%d][%d][%d]=%d\n",i,j,p,dp[j][p]);puts("");
		}
	}
	long long ans=0;
	for(int i=1;i<=k;i++) ans+=dp[v][i];
	cout<

练习

题目链接：垃圾陷阱

题意：有一头叫卡门的奶牛掉到了深度为$d$的井里，每个垃圾可以用来堆或者吃，对于第$i$个垃圾，它会在$t_i$的时刻扔进井里，可以堆$h_i$高，吃掉可以维持$f_i$个单位时间的生命。假设一开始卡门只能维持$10$个单位时间。问卡门最早什么时候可以爬出来，否则最长能活多久。

解析：定义$dp[i][j]$为前$i$个垃圾在高度为$j$的时候能存活的最长时间，则

情况$1$，选择吃，则需要保证在等第$i$个垃圾来的时候不能饿死，即$dp[i-1][j]-(t[i]-t[i-1])>=0$

有：$dp[i-1][j]+f[i]-(t[i]-t[i-1])$

情况$2$，选择堆，需要满足$j-h[i]>=0$

有：$dp[i-1][j-h[i]]-(t[i]-t[i-1])$

取两者最小值即可，具体实现的时候初始化为负无穷，$dp[0][0]=10$，代码如下：

#include
using namespace std;
const int N=105;
int n,m,k;
struct node
{
	int t,h,f;
	node(int t=0,int h=0,int f=0):t(t),h(h),f(f){}
}a[N];
int dp[N][N];
int cmp(node a,node b)
{
	return a.t>m>>n;
	for(int i=1;i<=n;i++) cin>>a[i].t>>a[i].f>>a[i].h;
	sort(a+1,a+n+1,cmp);
	memset(dp,-0x3f,sizeof(dp));
	dp[0][0]=10;
	for(int i=1;i<=n;i++)
	{
		for(int j=m;j>=0;j--)
		{
			if(dp[i-1][j]-(a[i].t-a[i-1].t)>=0)
				dp[i][j]=dp[i-1][j]+a[i].f-(a[i].t-a[i-1].t);//吃
			if(j>=a[i].h&&dp[i-1][j-a[i].h]-(a[i].t-a[i-1].t)>=0)
				dp[i][j]=max(dp[i][j],dp[i-1][j-a[i].h]-(a[i].t-a[i-1].t));//不吃
			if(dp[i][m]>=0)
			{
				cout<

题目链接：小A点菜

题意：有$n$个数字，每个数字最多只能使用$1$次，求拼成$x$的所有方案数。

解析：$01$背包计数即可，$dp[j]=dp[j]+dp[j-c[i]]$，代码如下：

#include
using namespace std;
const int N=50005;
int dp[N],a[N];
int main()
{
	int n,m;
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i];
	dp[0]=1;
	for(int i=1;i<=n;i++)
		for(int j=m;j>=a[i];j--) dp[j]+=dp[j-a[i]];
	cout<

题目链接：Cow Frisbee Team S

题意：有$n$个数字，每个数字最多只能使用$1$次，求拼成$x$的倍数的所有方案数。

解析：$01$背包计数即可，$dp[i][j]=dp[i][j]+dp[i-1][j]+dp[i-1][(j-c[i]+x)$，代码如下：

#include
using namespace std;
const int N=2005,M=100000000;
int n,m,k;
int a[N],dp[N][N];
int main()
{
	cin>>n>>m;
	for(int i=1;i<=n;i++) cin>>a[i],a[i]%=m;
	dp[0][0]=1;
	for(int i=1;i<=n;i++)
		for(int j=m-1;j>=0;j--)
			dp[i][j]=((dp[i][j]+dp[i-1][j])%M+dp[i-1][((j-a[i])+m)%m])%M;
	cout<

题目链接：粉刷匠

题意：windy有 N 条木板需要被粉刷。 每条木板被分为 M 个格子。 每个格子要被刷成红色或蓝色。windy每次粉刷，只能选择一条木板上一段连续的格子，然后涂上一种颜色。 每个格子最多只能被粉刷一次。如果windy只能粉刷 T 次，他最多能正确粉刷多少格子？一个格子如果未被粉刷或者被粉刷错颜色，就算错误粉刷。

解析：定义$dp[i][j][k][0/1]$代表到$(i,j)$时刷了$k$​次刷对，刷错当前格子下的所有正确分数格子数。

1. 换行时肯定要多刷一次

2. 若这一格与前一个格子颜色一样,最优的方式是把前一个的1状态原封不动转移,这时的0状态也跟着原封不动:$dp[i][j][k][1]=dp[i][j-1][k][1]+1;dp[i][j][k][0]=dp[i][j-1][k][0];$

3. 否则$[1]$就有两个选择: 一个换种颜色刷,另一个是继续上一格的颜色$dp[i][j][k][1]=max(dp[i][j-1][k-1][1]+1,dp[i][j-1][k][0]+1);$

   $[0]$也一样:$dp[i][j][k][0]=max(dp[i][j-1][k-1][0],dp[i][j-1][k][1]);$

代码实现如下：

#include
using namespace std;
const int N=51;
int n,m,t;
int a[N],dp[N][N][N*N][2];
char s[N][N];
int main()
{
	scanf("%d%d%d",&n,&m,&t);
	for(int i=1;i<=n;i++) scanf("%s",s[i]+1);
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
		{
			for(int k=1;k<=t;k++)
			{
				if(j==1)
				{
					dp[i][j][k][1]=max(dp[i-1][m][k-1][1],dp[i-1][m][k-1][0])+1;
					dp[i][j][k][0]=max(dp[i-1][m][k-1][1],dp[i-1][m][k-1][0]);
//					printf("dp[%d][%d][%d][%d]=%d ,",i,j,k,0,dp[i][j][k][0]);
//					printf("dp[%d][%d][%d][%d]=%d\n",i,j,k,1,dp[i][j][k][1]);
					continue;
				}
				if(s[i][j]==s[i][j-1]) 
				{
					dp[i][j][k][1]=dp[i][j-1][k][1]+1;
					dp[i][j][k][0]=dp[i][j-1][k][0];
				}
				else
				{
					dp[i][j][k][1]=max(dp[i][j-1][k-1][1]+1,dp[i][j-1][k][0]+1);
					dp[i][j][k][0]=max(dp[i][j-1][k-1][0],dp[i][j-1][k][1]);
				}
//				printf("dp[%d][%d][%d][%d]=%d ,",i,j,k,0,dp[i][j][k][0]);
//				printf("dp[%d][%d][%d][%d]=%d\n",i,j,k,1,dp[i][j][k][1]);
			}
		}
	int ans=max(dp[n][m][t][0],dp[n][m][t][1]);
	cout<

题目链接：排兵布阵

题意：每个人有$m$个士兵，可以把它们随意分配到$i$个城堡里，游戏采用逐个$1V1battle$的模式，如果在一次$battle$中第$i$城堡里你的士兵个数$>>$对方士兵个数的两倍，你就获得了$i$分。每次$battle$的策略必须一致，已知其余玩家的派兵情况，求总得分最大值。

解析：大概思路如下：

• 将一个城堡看作一组
• 先对每组城堡中的各个玩家的敌人数进行排序
• 每个玩家派兵的数量*2+1 可以看作为物品重量（注意玩家派兵数量可能相同）
• 那么 排序后该玩家敌人数的索引与城堡索引的乘积 就是物品价值 且每个组内的物品只能选择一次

于是我们就把这个问题转化为了分组背包问题，代码如下：

#include
using namespace std;
const int N=1005;
int n,m,s;
int a[N][N],b[N][N],dp[20005];
vectorv[N],w[N];
int cmp(int x,int y)
{
	return x>y;
}
int main()
{
	cin>>s>>n>>m;
	for(int i=1;i<=s;i++)
		for(int j=1;j<=n;j++)
			cin>>a[i][j],b[j][i]=a[i][j];
	for(int i=1;i<=n;i++)
	{
		sort(b[i]+1,b[i]+s+1,cmp);
		for(int j=1;j<=s;j++)
		{
			if(b[i][j]*2+1<=m)
			{
				v[i].push_back(b[i][j]*2+1);
				w[i].push_back((s-j+1)*i);
			}
		}
	}
	for(int i=1;i<=n;i++)
		for(int j=m;j>=1;j--)
			for(int k=0;k=v[i][k]) dp[j]=max(dp[j],dp[j-v[i][k]]+w[i][k]);
	cout<

题目链接：纪念品

题意：小伟突然获得一种超能力，他知道未来 $T$天$N$种纪念品每天的价格。某个纪念品的价格是指购买一个该纪念品所需的金币数量，以及卖出一个该纪念品换回的金币数量。

每天，小伟可以进行以下两种交易无限次：

1. 任选一个纪念品，若手上有足够金币，以当日价格购买该纪念品；
2. 卖出持有的任意一个纪念品，以当日价格换回金币。

每天卖出纪念品换回的金币可以立即用于购买纪念品，当日购买的纪念品也可以当日卖出换回金币。当然，一直持有纪念品也是可以的。

$T$天之后，小伟的超能力消失。因此他一定会在第 $T$天卖出所有纪念品换回金币。

小伟现在有 $M$ 枚金币，他想要在超能力消失后拥有尽可能多的金币。

解析：这是一道完全背包的题，我们进行 $t-1$轮完全背包:

把今天手里的钱当做背包的容量，把商品今天的价格当成它的消耗,把商品明天的价格当做它的价值，

每一天结束后把总钱数加上今天赚的钱，直接写背包模板即可。实现代码如下：

#include 
using namespace std;
const int N=1e5+5;
int dp[N],p[105][105];
int main()
{
	int t,n,m;
	cin>>t>>n>>m;
	for(int i=1;i<=t;i++)
		for(int j=1;j<=n;j++)
			cin>>p[i][j];
	for(int i=1;i

题目链接：多米诺骨牌

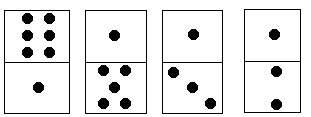
题意：多米诺骨牌由上下 $2$ 个方块组成，每个方块中有 $1\sim 6$ 个点。现有排成行的上方块中点数之和记为 $S_1$，下方块中点数之和记为 $S_2$，它们的差为 $\left|S_1-S_2\right|$。如图，$S1=6+1+1+1=9$，$S2=1+5+3+2=11$，$\left|S_1-S_2\right|=2$。每个多米诺骨牌可以旋转 $180°$，使得上下两个方块互换位置。请你计算最少旋转多少次才能使多米诺骨牌上下 $2$ 行点数之差达到最小。

对于图中的例子，只要将最后一个多米诺骨牌旋转 $180°$，即可使上下 $2$ 行点数之差为 $0$。

解析：题目要求的是最小差值情况下的最小交换次数，那么我们把其中一个计入状态里。记交换次数好像不太好做，所以我们要记的是差值。但是差值是一个绝对值，好像也不是很好表示，所以我们再来转化一下。观察到每次交换只是把上下两个数交换，故前i个骨牌上下两行数的总和是不变的，所以我们只需记录其中一行数字的和就可以知道差值了。这样状态就好表示了。$dp[i][j]$表示前$i$个数字，第一行的数字和是$j$时，最小的交换次数。初始值所有都$dp[i][j]$是无穷大，$dp[1][a[1]]=0$，$dp[1][b[1]]=1$。（a[]和b[]分别表示第一行和第二行的数字）

转移时，枚举每一个可能的和，共有6*n个，考虑当前一个交不交换即可.代码如下：

#include
using namespace std;
const int N=1005;
int n,a[N],b[N],s1[N],s2[N],dp[N][N*6]; 
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i]>>b[i];
		s1[i]=s1[i-1]+a[i];
		s2[i]=s2[i-1]+b[i];
	}
	memset(dp,0x3f,sizeof(dp));
	dp[1][a[1]]=0;dp[1][b[1]]=1;
	for(int i=2;i<=n;i++)
	{
		for(int j=6*n;j>=0;j--)
		{
			if(j-a[i]>=0) dp[i][j]=min(dp[i][j],dp[i-1][j-a[i]]);
			if(j-b[i]>=0) dp[i][j]=min(dp[i][j],dp[i-1][j-b[i]]+1);
		}
	}
	int Min=0x3f3f3f3f,ans=0,s=s1[n]+s2[n];
	for(int i=0;i<=s;i++)
	{
		if(dp[n][i]!=0x3f3f3f3f)
		{
			if(abs(i-(s-i))

题目链接：烹调方案

题意：一共有$n$件食材，每件食材有三个属性，$a_i$，$b_i$和$c_i$，如果在$t$时刻完成第$i$样食材则得到$a_i-t\ast b_i$的美味指数，用第$i$件食材做饭要花去$c_i$的时间。众所周知，$gw$的厨艺不怎么样，所以他需要你设计烹调方案使得美味指数最大。

解析：如果没有b[i]这个属性的话就是明显的01背包问题。

现在考虑相邻的两个物品x,y。假设现在已经耗费p的时间，那么分别列出先做x,y的代价：

a[x]-(p+c[x])*b[x]+a[y]-(p+c[x]+c[y])*b[y] (①)

a[y]-(p+c[y])*b[y]+a[x]-(p+c[y]+c[x])*b[x] (②)

对这两个式子化简，得到①＞②的条件是c[x]*b[y]

发现只要满足这个条件的物品对(x,y)，x在y前的代价永远更优。

因此可以根据这个条件进行排序，之后就是简单的01背包了。实现代码如下：

#include
using namespace std;
typedef long long ll;
const int N=1e5+5;
int n,V;
ll dp[N];
struct node
{
	ll a,b,c;
}a[N];
bool cmp(node x,node y)
{
	return x.c*y.b>V>>n;
	for(int i=1;i<=n;i++) cin>>a[i].a;
	for(int i=1;i<=n;i++) cin>>a[i].b;
	for(int i=1;i<=n;i++) cin>>a[i].c;
	sort(a+1,a+n+1,cmp);
	for(int i=1;i<=n;i++)
		for(int j=V;j>=0;j--)
			if(j-a[i].c>=0) dp[j]=max(dp[j],dp[j-a[i].c]+a[i].a-j*a[i].b);
	ll ans=0;
	for(int i=0;i<=V;i++) ans=max(ans,dp[i]);
	cout<

题目链接：Mooo Moo S

题意：$FJ$ 的 $N(1\le N\le 100)$ 个牧场都是沿着一条笔直的道路分布的。每一个牧场可能有许多种品种的奶牛； $FJ$ 拥有 $B(1\le B\le 20)$ 个不同品种的奶牛，而第 $i$ 种奶牛的叫声音量为 $V_i(1\le V_i\le 100)$ 。此外，有一股强风沿着道路吹来，将牛的叫声从左往右传递，如果某个牧场的总音量是 $x$ ，那么它将传递 $x-1$ 的音量到右边的下一个牧场。这就意味着，一个牧场里的总音量是处在该牧场的奶牛所发出的音量加上左边前一个牧场的总音量 $-1$ 。数据保证，每一个牧场内由该牧场所有奶牛所发出的总音量最多为$10^5$。

解析：我们可以通过每一个农场的总音量还原出该农场的牛产生的音量，然后就转化为了求$B$个数中最少取几个数可以凑成音量，这个直接用类似完全背包的状态转移方程即可。

#include
using namespace std;
typedef long long ll;
const int N=1e5+5;
int n,m,v[N],a[N],dp[N];
int main()
{
	cin>>n>>m;
	for(int i=1;i<=m;i++) cin>>v[i];
	for(int i=1;i<=n;i++) cin>>a[i];
	memset(dp,0x3f,sizeof(dp));
	dp[0]=0;
	for(int i=1;i<=m;i++)
		for(int j=v[i];j

题目链接：产品加工

题意：某加工厂有 A、B 两台机器，来加工的产品可以由其中任何一台机器完成，或者两台机器共同完成。由于受到机器性能和产品特性的限制，不同的机器加工同一产品所需的时间会不同，若同时由两台机器共同进行加工，所完成任务又会不同。某一天，加工厂接到 $n$ 个产品加工的任务，每个任务的工作量不尽一样。你的任务就是：已知每个任务在 A 机器上加工所需的时间 $t_1$，B 机器上加工所需的时间 $t_2$ 及由两台机器共同加工所需的时间 $t_3$，请你合理安排任务的调度顺序，使完成所有 $n$ 个任务的总时间最少。

解析：设$dp[j]$为执行了前$i$个任务，$A$机器已经做了$j$个时间时$B$机器做的最少时间。

给$A$做，为：$dp[j-t_1[i]]$

给$B$做，为：$dp[j]+t_2[i]$

交给$A$和$B$一起做，为：$dp[j-t_3[i]]+t_3[i]$

$ans=mi{n}_{i=1}^{up}max(i,dp[i])$

代码如下：

#include
using namespace std;
typedef long long ll;
const int N=1e5+5,inf=0x3f3f3f3f;
int n,m,v[N],a[N],dp[N],t1[N],t2[N],t3[N];
int main()
{
	cin>>n;
	for(int i=1;i<=n;i++) cin>>t1[i]>>t2[i]>>t3[i];
	memset(dp,0x3f,sizeof(dp));
	dp[0]=0;
	int up=0;
	for(int i=1;i<=n;i++)
	{
		up+=max(t1[i],t3[i]);
		for(int j=up;j>=0;j--)
		{
			int tmp1=inf;
			if(j-t1[i]>=0&&t1[i]) tmp1=dp[j-t1[i]];
			int tmp2=inf;
			if(t2[i]) tmp2=dp[j]+t2[i];
			int tmp3=inf;
			if(j-t3[i]>=0&&t3[i]) tmp3=dp[j-t3[i]]+t3[i];
			dp[j]=min(tmp1,min(tmp2,tmp3));
		}
	}
	int ans=inf;
	for(int i=1;i<=up;i++) ans=min(ans,max(i,dp[i]));
	cout<

题目链接：商店购物

题意：三朵花的价格是 $5$ 而不是 $6$ ，$2$ 个花瓶和一朵花的价格是 $10$ 而不是 $12$ 。 请编写一个程序，计算顾客购买一定商品的花费，尽量地利用优惠使花费最少。尽管有时候添加其他商品可以获得更少的花费，但是你不能这么做。对于上面的商品信息，购买三朵花和两个花瓶的最少花费的方案是：以优惠价购买两个花瓶和一朵花（$10$），以原价购买两朵花（$4$）。

解析：完全背包题，这里背包中物品的价值的是每种组合优惠的钱数 ，用单买所有需要物品的价格减去这个最大的优惠。然后5维背包即可。代码如下：

#include
using namespace std;
typedef long long ll;
const int N=1e5+5,inf=0x3f3f3f3f;
int s,n;
int cnt[1005][1005],dp[7][7][7][7][7];
int a[1005],tot,p1[1005],b,num[1005],pr[1005],val[1005];
int main()
{
	cin>>s;
	for(int i=1;i<=s;i++)
	{
		cin>>n;
		int c,k;
		for(int j=1;j<=n;j++)
		{
			cin>>c>>k;
			if(!a[c]) a[c]=++tot;
			cnt[i][a[c]]=k;
		}
		cin>>p1[i];
	}
	cin>>b;
	int sum=0;
	for(int i=1;i<=b;i++)
	{
		int c,k,p;
		cin>>c>>k>>p;
		num[a[c]]=k;
		pr[a[c]]=p;
		sum+=k*p;
	}
	for(int i=1;i<=s;i++)
	{
		for(int j=1;j<=tot;j++)
			val[i]+=cnt[i][j]*pr[j];
		val[i]-=p1[i];
	}
	for(int i=1;i<=s;i++)
		for(int i1=cnt[i][1];i1<=num[1];i1++)
			for(int i2=cnt[i][2];i2<=num[2];i2++)
				for(int i3=cnt[i][3];i3<=num[3];i3++)
					for(int i4=cnt[i][4];i4<=num[4];i4++)
						for(int i5=cnt[i][5];i5<=num[5];i5++)
							dp[i1][i2][i3][i4][i5]=max(dp[i1][i2][i3][i4][i5],
							dp[i1-cnt[i][1]][i2-cnt[i][2]][i3-cnt[i][3]][i4-cnt[i][4]][i5-cnt[i][5]]+val[i]);
	cout<

题目链接：The Fewest Coins G

题意：农夫John想到镇上买些补给。为了高效地完成任务，他想使硬币的转手次数最少。即使他交付的硬 币数与找零得到的的硬币数最少。 John想要买价值为T的东西。有N(1<=n<=100)种货币参与流通，面值分别为V1,V2…Vn (1<=Vi<=120)。John有Ci个面值为Vi的硬币(0<=Ci<=10000)。我们假设店主有无限多的硬币， 并总按最优方案找零。注意无解输出-1。

解析：首先，我们设买家总共支付 $x$元，那么卖家就是找零$x-m$ 元，其实要凑齐 $x$ 元，就是对于买家做一个多重背包 $dp1$ ，对于卖家，再做一个完全背包$dp2$ ，然后枚举$x$ ，求出最优解即可。由于$n=100$，算法复杂度又是$n\ast V\ast log(V)$量级的，盲猜上界$V=1e5$。代码实现如下：

#include
using namespace std;
typedef long long ll;
const int N=1e5+5,inf=0x3f3f3f3f;
int dp1[N],dp2[N],V,n,v[N],c[N];
int main()
{
	memset(dp1,0x3f,sizeof(dp1));memset(dp2,0x3f,sizeof(dp2));
	cin>>n>>V;
	for(int i=1;i<=n;i++) cin>>v[i];
	for(int i=1;i<=n;i++) cin>>c[i];
	dp1[0]=0;
	for(int i=1;i<=n;i++) 
	{
		for(int k=1;k<=c[i];k<<=1)
		{
			for(int j=N-1;j>=k*v[i];j--) dp1[j]=min(dp1[j],dp1[j-k*v[i]]+k);
			c[i]-=k;
		}
		for(int j=N-1;j>=c[i]*v[i];j--) dp1[j]=min(dp1[j],dp1[j-c[i]*v[i]]+c[i]);
	}
	dp2[0]=0;
	for(int i=1;i<=n;i++)
		for(int j=v[i];j<=N-1;j++)
			dp2[j]=min(dp2[j],dp2[j-v[i]]+1);
	int ans=inf;
	for(int i=V;i

完结！22题的文章写了一天，好累呀。