go的sort包源码分析与排序算法解析
1、sort包的使用
Sort函数的源码:
func Sort(data Interface) {
n := data.Len()
quickSort(data, 0, n, maxDepth(n))
}
再看Interface的类型,是一个包含了三个函数的接口类型:
type Interface interface {
// Len is the number of elements in the collection.
Len() int
Less(i, j int) bool
// Swap swaps the elements with indexes i and j.
Swap(i, j int)
}
任何实现了接口Interface的类型,都可以作为Sort函数的入参去执行排序操作。
type Person struct {
Name string
Age int
}
type ByAge []Person
func (a ByAge) Len() int { return len(a) }
func (a ByAge) Swap(i, j int) { a[i], a[j] = a[j], a[i] }
func (a ByAge) Less(i, j int) bool { return a[i].Age < a[j].Age }
func Example() {
people := []Person{
{"Bob", 31},
{"John", 42},
{"Michael", 17},
{"Jenny", 26},
}
sort.Sort(ByAge(people))
}
2、quickSort
Sort函数的核心是quickSort。虽然quickSort如它的名字一样,核心是快速排序,但是它的实现,是多种排序算法的集合,以满足各种不同条件下排序的最优空间复杂度和时间复杂度。
func quickSort(data Interface, a, b, maxDepth int) {
for b-a > 12 { // Use ShellSort for slices <= 12 elements
if maxDepth == 0 {
heapSort(data, a, b)
return
}
maxDepth--
mlo, mhi := doPivot(data, a, b)
// Avoiding recursion on the larger subproblem guarantees
// a stack depth of at most lg(b-a).
if mlo-a < b-mhi {
quickSort(data, a, mlo, maxDepth)
a = mhi // i.e., quickSort(data, mhi, b)
} else {
quickSort(data, mhi, b, maxDepth)
b = mlo // i.e., quickSort(data, a, mlo)
}
}
if b-a > 1 {
// Do ShellSort pass with gap 6
// It could be written in this simplified form cause b-a <= 12
for i := a + 6; i < b; i++ {
if data.Less(i, i-6) {
data.Swap(i, i-6)
}
}
insertionSort(data, a, b)
}
}
首先,如果排序长度小于12,则采用shell排序的思想对数组做个处理。然后做基本得插入排序。如果长度大于12,则采用快速排序处理。同时为了保证递归的深度,最大递归深度与长度有关,深度计算源码如下所示:
func maxDepth(n int) int {
var depth int
for i := n; i > 0; i >>= 1 {
depth++
}
return depth * 2
}
保证了递归的最大深度为log2(数组长度),避免了长度数组过大,一直递归带来的栈溢出问题。快速排序切分完以后,采用的堆排序,不需要再额外分配内存空间,直接在原切片上构造大顶堆或者小顶堆,做堆排序。
3、插入排序
插入排序的核心思想是通过构建有序序列,对于未排序的数据,在已排序序列中,从后往前扫描,找到合适的位置插入。一个生活中常用的场景:抓扑克牌的时候,把后抓的牌,插入到前面已排序好的扑克牌中。实现逻辑:
1、从第一个开始,可以认为这个元素是已经排序好的。因此循环遍历的时候,是从第二元素开始。
2、取出这个元素,在已排序好的元素列表中后往前扫描
3、如果该元素(排序好的列表中)大于新插入的元素,则将新插入的元素与这个元素交换。
4、重复步骤3,直到已排序好的元素列表中碰到比新插入的元素小或者到达已排序号数组的顶端。
5、对待插入的元素重复步骤2、3、4,直到待插入的元素全部插入。
插入流程图如下图所示:
插入排序的源码如下所示:
// insertionSort sorts data[a:b] using insertion sort.
func insertionSort(data Interface, a, b int) {
for i := a + 1; i < b; i++ {
for j := i; j > a && data.Less(j, j-1); j-- {
data.Swap(j, j-1)
}
}
}
4、shell排序
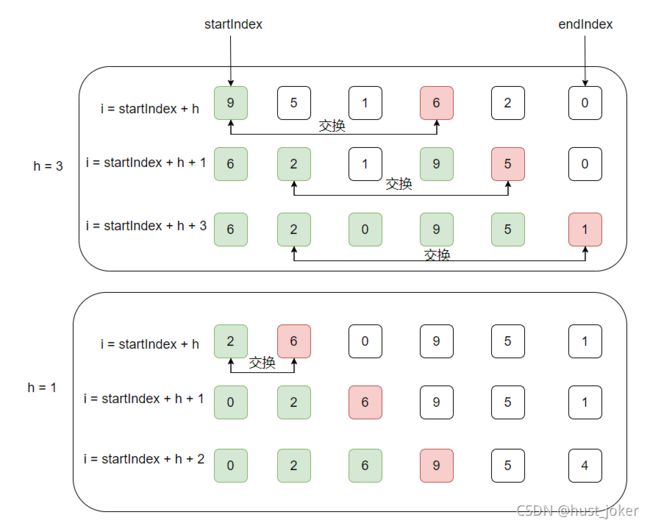
shell排序的核心思想依然是插入排序。与插入排序不同的是,shell排序优化了在大数组时的排序性能。从前面的分析可以看出插入排序只交换相邻的两个元素。如果最小的那个值恰巧在最后一个,用插入排序的话,就需要N-1次交换。shell排序增加了一个步长的概念,每次元素的交换不再从相邻元素开始,而是跨过一个步长。能过做到快速的移动在数组尾端的元素。流程示意图如下所示:
shell排序的源码实现:
// insertionSort sorts data[a:b] using insertion sort.
func shellSort(data Interface, a, b int) {
h := 1
for ; h < (b - a)/2; {
h = h*2 + 1
}
for ; h >= 1; {
for i := a + h; i < b; i++ {
for j := i; j >= h && data.Less(j, j-h); j=j-h {
data.Swap(j, j-h)
}
}
}
}
查看quickSort的源码发现,其实针对长度小于12的数组,go并没有严格的用shell排序去做。只是对偏移量大于6的数组的上半区(偏移量大于其实地址+6的部分)做了一次简单的数据交换,然后再做插入排序。
if b-a > 1 {
// Do ShellSort pass with gap 6
// It could be written in this simplified form cause b-a <= 12
for i := a + 6; i < b; i++ {
if data.Less(i, i-6) {
data.Swap(i, i-6)
}
}
insertionSort(data, a, b)
}
5、快速排序
5.1、标准快速排序
快速排序实际上一种分治算法的排序。它把一个数组分成两个部分,然后独立的排序两个子数组。快速排序切分点取决于数组的内容。一般为了保证切分点的随机性,会随机洗整个数组。然后用第一个元素作为切分点分割数组,接着继续对两个子数组做排序。分割的最终目的是把数组分成分成三部分:
1、a[j]放到排序好的数组里它最终的位置
2、从a[low]到a[j-1]中的每个元素都不大于a[j]
3、从a[j+1]到a[high]中的每个元素都不小于a[j]
如此一来,如果左边的数组是排序好的,右边的数组也是排序好的,那么整个数组就是排序好的。采用递归的方式,就能得到一个排序好的数组。伪代码如下:
func quickSort {
if low >= high {
return
}
k = partition() // 找到第一个元素原本该属的位置,数组分为上下部分,比它都大的一部分和都小的一部分
quickSort(上半部分)
quickSort(下半部分)
}
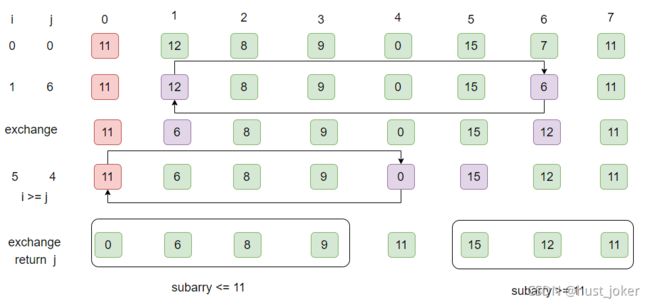
分割数组是整个算法的核心。一般的做法如下:
1、随机的选择a[low]作为分割元素。
2、从左往右扫描数组,找到第一个比它大的数。
3、从右往左找到第一个比它小的数。
4、因为这两个数以选择的分割元素来看,是乱序的。因此交换它们。
5、重复2 3 4 直到向右的索引i大于了向左的索引j。
6、交换a[low]和a[j],并返回j。j就是分割元素本来该存在的位置。
分割源码:
func patition(array []int, int low, int high) int {
i := low + 1
j := high
v := array[low]
for ;; {
for ; array[i] <= v; {
i++
if i == high {
break
}
}
for ; array[j] >= v; {
j--
if j == low {
break
}
}
if i >= j {
break
}
array[i], array[j] = array[j], array[i]
}
array[low], array[j] = array[j], array[low]
return j
}
快速排序递归实现:
func quickSort(array []int, low int, high int) {
if low >= high {
return
}
k := partition(array, low, high)
quickSort(array, low, k-1)
quickSort(array, k+1, high)
}
5.2、优化快速排序
选取待排序slice的首个、中间和尾部三个元素排序,取中间元素做轴,进行快速排序。减少了最坏情况发生的概率和数组越界时的比较次数。同时针对数组过长的情况,由左中右三个中选取,扩大到9个元素中去选取。
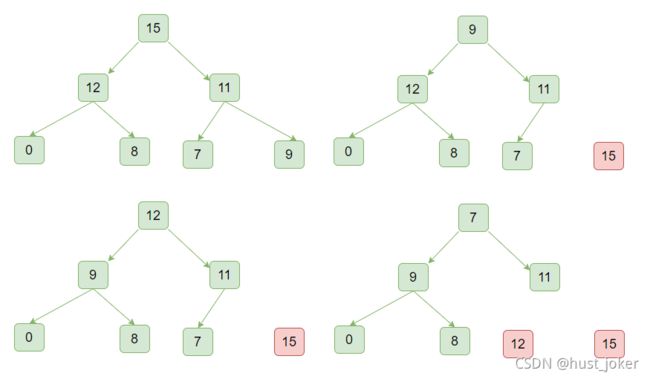
6、堆排序
6.1、 二叉堆
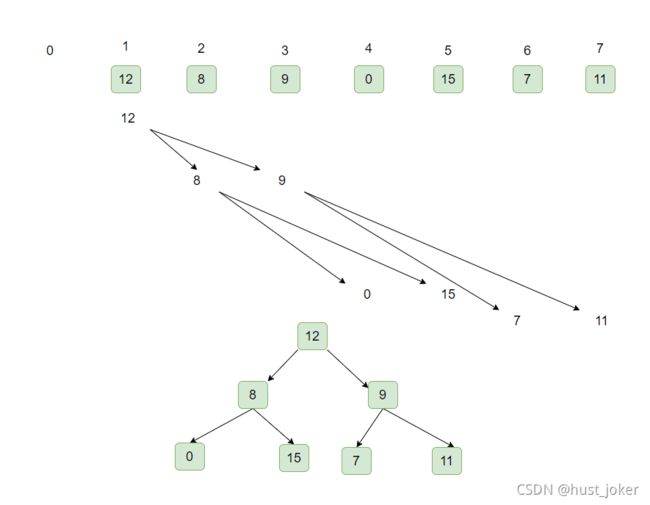
二叉堆是一个数据结构:父节点的值总是大于等于两个子节点的值。从一个节点往上走,总能得到一个非递减的序列。从一个节点往下走,总能得到一个非递增的序列。
二叉堆有几种表现形式:二叉树和二叉数组。着重介绍二叉堆的数组形式。
可以把每一个节点的位置认为是k,那么它的父节点是k/2,两个子节点分别是kx2和kx2+1。那么任意一个数组都可以构成一个二叉堆。
从3号元素9,像数组左侧开始遍历,采用下沉的方式构造出大顶堆:
找到子节点中较大的值,比较当前元素与这个值,如果当前节点比这个值小,则交换当前节点与该子节点的值。
sort包源码:
// siftDown implements the heap property on data[lo:hi].
// first is an offset into the array where the root of the heap lies.
func siftDown(data Interface, lo, hi, first int) {
root := lo
for {
child := 2*root + 1
if child >= hi {
break
}
if child+1 < hi && data.Less(first+child, first+child+1) {
child++
}
if !data.Less(first+root, first+child) {
return
}
data.Swap(first+root, first+child)
root = child
}
}
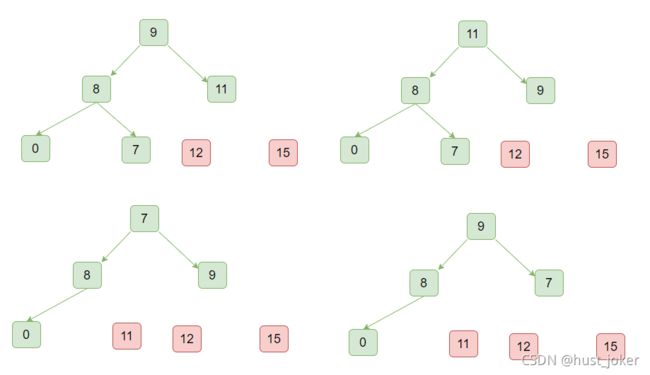
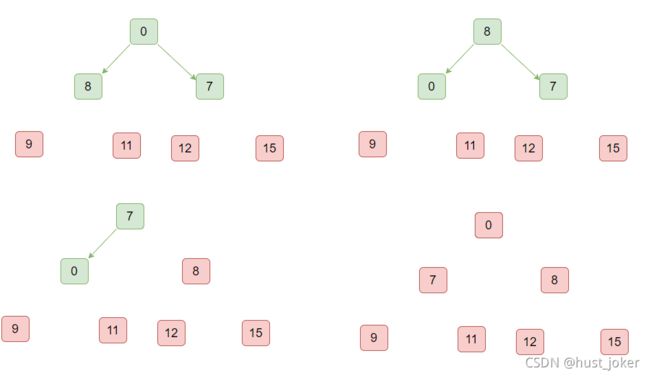
6.2、 堆排序
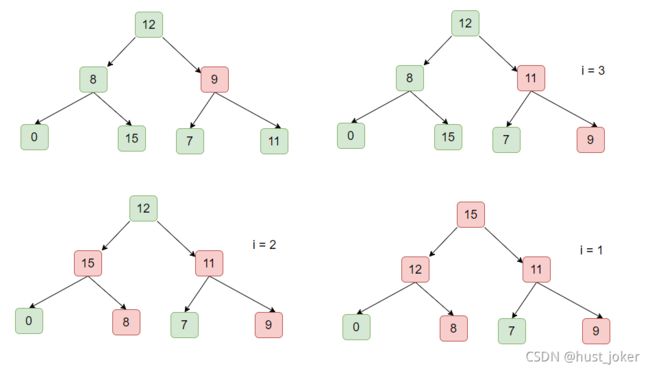
所谓堆排序,就是利用前面的构造的大顶堆:
1、用堆顶的第一个元素和最后一个元素做交换。
2、将最后一个元素出堆,排出在下一次构造大顶堆的过程
3、将第一个元素做下沉操作。放到合适的位置,构造新的大顶堆。
4、重复1 2 3直到二叉堆的大小为1.
sort包源码:
func heapSort(data Interface, a, b int) {
first := a
lo := 0
hi := b - a
// Build heap with greatest element at top.
for i := (hi - 1) / 2; i >= 0; i-- {
siftDown(data, i, hi, first)
}
// Pop elements, largest first, into end of data.
for i := hi - 1; i >= 0; i-- {
data.Swap(first, first+i)
siftDown(data, lo, i, first)
}
}
7、总结。
sort包里面的排序实现,核心思想仍然是快速排序。但是针对不同的场景做了很多细致的优化。
1、小长度直接采用插入排序和shell排序的优化。
2、控制快速排序的递归深度,防止栈溢出。
3、对传统的快速排序的选轴做了优化。对队首、对中和对尾的元素进行排序。取中间元素做轴。减少了最坏情况发生的概率。
4、对于切分后的子数组采用堆排序的方式。