位运算——异或运算
目录
-
- 按位异或运算(^)
- 异或运算的应用
-
- 镜子田地
- 镜子
按位异或运算(^)
按位异或运算将两个运算分量的对应位按位遵照以下规则进行计算:
0 ^ 0 = 0, 0 ^ 1 = 1, 1 ^ 0 = 1, 1 ^ 1 = 0
即相应位的值相同的,结果为 0,不相同的结果为 1。
例如,2 ^ 6结果为4
因为2表示为二进制为0010,6表示为二进制为0110
两数只有第三位相异,因此最后的结果为0100,即为4
了解异或运算的用法,我们来看看异或运算在算法题中的应用。
异或运算的应用
镜子田地
题目描述
农夫约翰在屋子外面放了一些旧镜子,他的奶牛们像往常一样调皮地偷走了它们!
奶牛们将镜子放置在了一个矩形田地中,该田地可被划分为 N × M N×M N×M个方格区域。
在每个方格区域中,奶牛在其某对对角之间放置一个双面镜,因此,共有两种放法,一种为
/放置(镜子连接方格左下角和右上角),另一种为\放置(镜子连接方格左上角和右下角)。一天晚上,奶牛贝茜将激光发射器带到了该田地中。
她站在田地外面,沿着田地的行或列水平或垂直照射光束,使光束反射一定数量的镜子。
由于镜子都是沿对角线摆放,因此经反射镜反射的水平光束最终将垂直传播,反之亦然。
贝茜想知道从田地之外射入的水平或垂直光束最多可以在田地中被反射多少次。
给定镜子田地的布局,请帮助贝茜计算这个数字。
输入格式
第一行包含 N N N和 M M M。
接下来 N N N行,每行包含 M M M个
/或\字符,表示田地中镜子的具体摆放方式。
输出格式
输出田地之外的水平或垂直光束能够被反射的最大次数。
如果可以无限反射,则输出 −1。
数据范围
1 ≤ N , M ≤ 1000 1≤N,M≤1000 1≤N,M≤1000
输入样例:
3 3
/\\
\\\
/\/
输出样例:
3
样例解释
贝茜可以从上向下沿中间列上方发射激光。
共可以反射 3 次。
题目分析
一定不会无限反射,因为这些镜子是相邻的,无限反射是需要有入口的。
我们可以枚举从每条边射入的位置进行搜索。
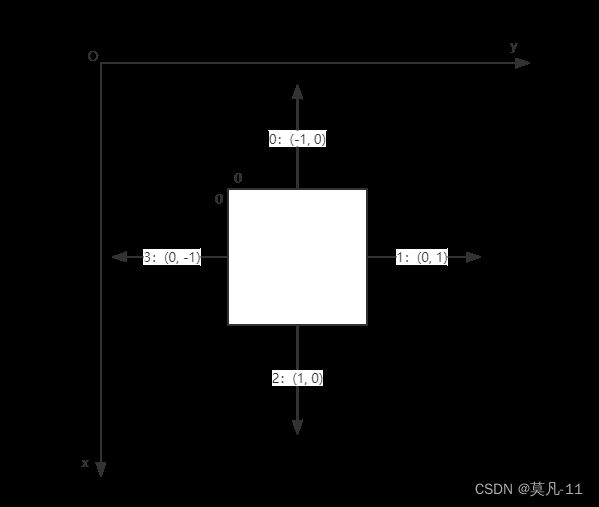
我们要清楚,任意一个数a异或同一个数两次后值依旧为a,比如7^3,结果为4,4^3后,结果仍然为7。
那么当镜子为/时,0→1、1→0、2→3、3→2。d ^= 1
当镜子为\时,0→3、3→0、1→2、2→1。d ^= 3
代码如下
#include 镜子
题目描述
农夫约翰的奶牛在农场周围造成了太多麻烦,因此约翰希望对它们保持更密切的关注。
通过在农场的各个位置安装 N N N个反光围栏,他希望能够从 ( 0 , 0 ) (0,0) (0,0)位置的房子看到 ( a , b ) (a,b) (a,b)位置的牛棚。
在约翰农场的二维平面图中,围栏 i i i表示为以整数位置坐标 ( x i , y i ) (x_{i},y_{i}) (xi,yi)为中心的倾斜 45 45 45度(如/或\)的短线段。
例如,以 ( 3 , 5 ) (3,5) (3,5)为中心,形如/的围栏可以描述为从 ( 2.9 , 4.9 ) (2.9,4.9) (2.9,4.9)到 ( 3.1 , 5.1 ) (3.1,5.1) (3.1,5.1)的线段。
每个围栏(以及牛棚的位置)位于不同的位置。
( 0 , 0 ) (0,0) (0,0)和 ( a , b ) (a,b) (a,b)处无围栏。
约翰计划坐在他的房屋 ( 0 , 0 ) (0,0) (0,0)处,并直接向右(沿 + x +x +x方向)看。
当他的目光从农场的一些反光围栏上反射出来时,他希望能够看到点 ( a , b ) (a,b) (a,b)。
不幸的是,他认为其中一个反光围栏的摆放朝向不对,例如应该为/,却摆成了\。
请输出给定反光围栏中,第一个能够通过改变其朝向使得约翰成功看到点 ( a , b ) (a,b) (a,b)的围栏的顺序编号。
如果约翰不需要切换任何围栏的朝向就已经可以看到点 ( a , b ) (a,b) (a,b)则输出 0 0 0。
如果约翰无法通过切换单个围栏的朝向使自己看到点 ( a , b ) (a,b) (a,b)则输出 − 1 −1 −1。
输入格式
第一行包含三个整数 N , a , b N,a,b N,a,b。
接下来 N N N行,其中第 i i i行描述第 i i i号围栏的位置和朝向。首先包含两个整数 x i , y i x_{i},y_{i} xi,yi表示其中心点位置,然后包含一个字符/或\表示围栏朝向。
围栏编号从 1 1 1开始。
输出格式
输出第一个能够通过改变其朝向使得约翰成功看到点 ( a , b ) (a,b) (a,b)的围栏的顺序编号。
如果约翰不需要切换任何围栏的朝向就已经可以看到点 ( a , b ) (a,b) (a,b)则输出 0 0 0。
如果约翰无法通过切换单个围栏的朝向使自己看到点 ( a , b ) (a,b) (a,b)则输出 − 1 −1 −1。
数据范围
1 ≤ N ≤ 200 1≤N≤200 1≤N≤200,
− 106 ≤ x i , y i , a , b ≤ 106 −106≤x_{i},y_{i},a,b≤106 −106≤xi,yi,a,b≤106
输入样例:
5 6 2
3 0 /
0 2 /
1 2 /
3 2 \
1 3 \
输出样例:
4
样例解释
农场的平面图如下所示,其中 H H H表示约翰的房子, B B B表示牛棚:
3 .\..... 2 //.\..B 1 ....... 0 H../... 0123456通过改变 ( 3 , 2 ) (3,2) (3,2)处的围栏朝向,就可以使约翰看到点 ( a , b ) (a,b) (a,b),如下所示:
3 .\..... 2 //./--B 1 ...|... 0 H--/... 0123456 ```
题目分析
无
代码如下
#include