启发式搜索求解TSP近似解

一、 实验要求
TSP (旅行商) 问题是运筹学和最优化理论等领域的经典问题,它已证明是NP(Nondeterministic Polynomial)完全问题,到目前为止, 所有的NP完全问题都还没有多项式时间算法。TSP问题的求解算法通常分为两类:一类是精确求解;另一类是近似求解。
本实验要求采用启发式搜索算法求解TSP问题的近似解，采用C系列语言编程实现, 数据源于TSP LIB(城市间的距离四舍五入以整数计算)。
二、 算法的基本思想或者流程
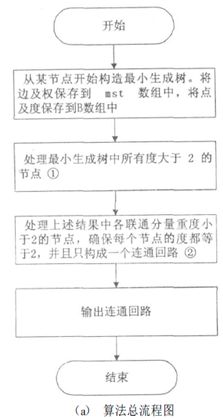
首先利用最小生成树算法构造无向图 G 的TSP问题的最小生成树；然后从最小生成树开始构造闭合回路(N个城市不重复排列序列)；最后采用枚举的方法,确定从不同最小生成树开始构造的闭合回路中距离最小的一个 ,即最短城市序列 。
由于闭合回路中每个节点的度都为2 ,因此在构造闭合回路时需要处理最小生成树中度不等于2的节点。
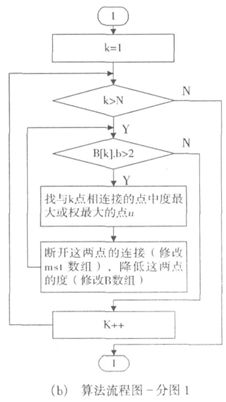
处理时,第一步是通过删除边的方法降低最小生成树中度大于2的节点的度 ,保证每个节点的度都不大2。删除边时,首先选择与待处理节点(度大于2的节点)相连接的节点中度最大的节点,
如果被选择节点的度大于2 ,则删除这两节点之间的边,降低这两节点的度。
否则,选择与待处理节点相连接的节点中权值大的节点,删除这两节点之间的边 ,降低这两节点的度。
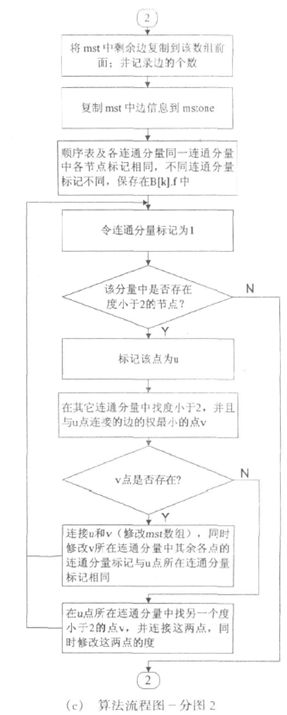
第二步是通过连接的方法 , 连接最小生成树中度小于2 的节点。
连接时为了保证所有节点在同一个连通分量中 ,
首先标记各连通分量 ,
然后选择不同连通分量中度小于 2 的节点并且两点之间权值小的点进行连接 ,从而构成一个大的连通分量 ,
最后连接同一个连通分量中仅有的两个度为 1 的节点 , 从而构成一个闭合回路 。
从不同节点开始生成最小生成树并构造闭合回路的计算是相互独立的 ,因此 ,可以采用并行计算的方法生成最小生成树并构造闭合回路 ,然后比较各回路的距离值 ,从而确定最佳闭合回路(城市序列)。由于 N 个城市的顶点集的最小生成树的数量远远小于顶点个数 ,因此比较各回路的距离值 , 确定最佳闭合回路算法的时间复杂度小于 O(N)。

#include    

#define MAX 100  
#define MAXCOST 0x7fffffff  
  
int minstdu[MAX];//最小生成树每个顶点的度 ，minstdu[1]=1表示顶点1的度为1 
int mstcostnum;//最小生成树中边的条数 
int minst[MAX][MAX];//最小生成树 
int Connected[MAX];//标记连通分量，Connected[1]=1表示顶点1处在连通分量1中 
int graph[MAX][MAX];//保存输入的带权无向图 
int sum[MAX];//保存各回路的距离值，例如sum[1]=10表示顶点1的最小生成树生成的回路距离值为10.

int mstMAXdu(int a, int n) //求最小生成树中除了点a的点的最大的度 
{
	int mstmaxdu = 0;
	for(int i = 1; i <= n; i++)
	{		
		if(a!=i&&minstdu[i]>mstmaxdu)
		{
			mstmaxdu = minstdu[i];
		}		
	}
	return mstmaxdu;
}

int mstMAXdupt(int a, int b, int n)//求最小生成树中除了点a的点的度为b的点 
{
	int pt = 0;
	for(int i = 1; i <= n; i++)
	{
		if(a!=i&&minstdu[i]==b)
		{
			pt = i;
		}
	}
	return pt;
}

int mstMAXcost(int a, int n)//求最小生成树中与点a相连的最大的边 
{
	int maxcost = 0;
	for(int i = 1; i <= n; i++)
	{
		if(a!=i&&minst[a][i]>maxcost)
		{
			maxcost	= minst[a][i];
		}
	}
	return maxcost;
}
  
int mstMAXcostpt(int a, int b, int n)//求最小生成树中与点a相连的边为b的点 
{
	int pt = 0;
	for(int i = 1; i <= n; i++)
	{
		if(a!=i&&minst[a][i]==b)
		{
			pt = i;
		}
	}
	return pt;
}
  
void prim(int graph[][MAX], int n)  //prim算法求最小生成树 
{  
    int lowcost[MAX];  
    int mst[MAX];  
    int a, i, j, min, minid, sum = 0;  
    for (i = 2; i <= n; i++)  
    {  
        lowcost[i] = graph[1][i];//lowcost存放顶点1可达点的路径长度 
        mst[i] = 1;//初始化以1位起始点 
    }  
    mst[1] = 0;  
    
    for (i = 2; i <= n; i++)  
    {  
        min = MAXCOST;  
        minid = 0;  
        for (j = 2; j <= n; j++)  
        {  
            if (lowcost[j] < min && lowcost[j] != 0)  
            {  
                min = lowcost[j];//找出权值最短的路径长度 
                minid = j; //找出最小的ID 
            }  
        }  
        printf("V%d-V%d=%d\n",mst[minid],minid,min);
        a = mst[minid];
		minst[a][minid] = min;
		minst[minid][a] = min;
		minstdu[a] = minstdu[a] + 1;
		minstdu[minid] = minstdu[minid] + 1;
		mstcostnum++; 
        sum += min;//求和 
        lowcost[minid] = 0;//该处最短路径置为0 
        for (j = 2; j <= n; j++)
        {  
            if (graph[minid][j] < lowcost[j])//对这一点直达的顶点进行路径更新 
            {  
                lowcost[j] = graph[minid][j];  
                mst[j] = minid;
            }  
        }  
    }  
} 
 
int main()  
{  
    int i, j, k, m, n;  
    int x, y, cost, APEX;
	int maxdu, maxdupoint, maxmstcost, maxmstcostpoint, minnum; 
	printf("--------采用启发式搜索求解TSP问题--------\n"); 
    printf("请输入无向图的顶点的个数与边的个数:\n"); 
    scanf("%d %d",&m,&n);//m=顶点的个数，n=边的个数  
    
    for (i = 1; i <= m; i++)//初始化图 
    {  
        for (j = 1; j <= m; j++)  
        {  
            graph[i][j] = MAXCOST;  
        }  
    }  
	printf("请输入无向图的每条边的权:\n(输入1 2 3表示顶点1与顶点2的边的权为3)\n");  
    for (k = 1; k <= n; k++)  
    {  
    	scanf("%d %d %d",&i,&j,&cost);
        graph[i][j] = cost;  
        graph[j][i] = cost;  
        minst[i][j] = 0;  
        minst[j][i] = 0; 
        minstdu[i] = 0;
        minstdu[j] = 0;
        Connected[i] = 0;
        Connected[j] = 0;
        sum[i] = 0;
        sum[j] = 0;
    }  
    mstcostnum = 0;
    for(APEX = 1; APEX <= m;APEX++)
	{
    	printf("以顶点%d构造最小生成树\n",APEX);
		prim(graph, m);//用prim算法从顶点1生成最小生成树 
	
		for(k = 1; k <= m; k++)//第一步,降低最小生成树中度大于2的节点的度 ,保证每个节点的度都不大2。
		{
			if(minstdu[k]>2)
			{
				maxdu = mstMAXdu(k,m); //最小生成树中除了K的最大的度 
				maxdupoint = mstMAXdupt(k,maxdu,m);
				if(maxdu>2)
				{
					minst[k][maxdupoint] = 0;
					minst[maxdupoint][k] = 0;
					minstdu[k]--;
					minstdu[maxdupoint]--;
					mstcostnum--;//边 
				}
				else//找权值最大的 
				{
					maxmstcost = mstMAXcost(k,m);  
					maxmstcostpoint = mstMAXcostpt(k,maxmstcost,m);
					minst[k][maxmstcostpoint] = 0;
					minst[maxmstcostpoint][k] = 0;
					minstdu[k]--;
					minstdu[maxmstcostpoint]--;
					mstcostnum--; 
				}
			}
		} 
		
		
		for(;mstcostnum<m;)//第二步是通过连接的方法 , 连接最小生成树中度小于2 的节点
		{
			for(i = 1; i <= m; i++)//标记连通分量 
			{
				if(minstdu[i]==0)
				{
					Connected[i] = i;
				}
				else
				{
					for(j = 1; j <= m; j++)
					{
						if(i!=j&&minst[i][j]!=0)
						{
							if(Connected[i]==0)
							{
								Connected[i] = i;
							}
							Connected[j] = Connected[i];
						}
					}
				}
			}
			
			for(i = 1; i <= m; i++)//连接最小生成树中度小于2 的节点 
			{
				if(minstdu[i]<2)
				{
					for(j = 1; j <= m; j++)
					{
						if(i!=j && Connected[j]!=Connected[i] && minstdu[j]<2)
						{
							minst[i][j] = graph[i][j];
							minst[j][i] = graph[i][j];
							minstdu[i]++;
							minstdu[j]++;
							mstcostnum++;
							x = Connected[i];
							y = Connected[j];
							for(k = 1; k <= m; k++)
							{
								if(Connected[k]==y)
								{
									Connected[k] = x;
								}
							}
						}
					}
					if(minstdu[i]<2)
					{
						for(j = 1; j <= m; j++)
						{
							if(i!=j && Connected[j]==Connected[i] && minstdu[j]<2)
							{
								minst[i][j] = graph[i][j];
								minst[j][i] = graph[i][j];
								minstdu[i]++;
								minstdu[j]++;
								mstcostnum++;
							}
						}
					}
				}
			}
			
		}
//		printf("输出此路径及其距离为：\n");
		for(i = 1, j = 1, x = 0; i <= m; i++)//输出路径 
		{
			for(k = 1; k <= m; k++)
			{
				if(j!=k&&k!=x&&minst[j][k]!=0)
				{
					printf("%d->%d:%d\n",j,k,minst[j][k]);
					sum[APEX] = sum[APEX] + minst[j][k];
					x = j;
					j = k;
					break;
				}
			}
		}
//		printf("此路径距离值为：%d\n",sum[APEX]);
//	    
		if(APEX>1)//若已经替换过初始点，则恢复成原图 
		{
			for(i = 2; i <= m; i++)
		    {
		    	if(i!=APEX)
		    	{
			    	cost = graph[1][i];
					graph[1][i] = graph[APEX][i];
					graph[i][1] = graph[APEX][i];
			    	graph[APEX][i] = cost;
			    	graph[i][APEX] = cost;
				}
			}
		}
		//重设顶点	
	    //APEX++;
	    for(i = 2; i <= m; i++)
	    {
	    	if(i!=APEX)
	    	{
		    	cost = graph[1][i];
				graph[1][i] = graph[APEX][i];
				graph[i][1] = graph[APEX][i];
		    	graph[APEX][i] = cost;
		    	graph[i][APEX] = cost;
			}
		}
		//重设顶点后需要初始化   
	    for(i = 0; i<=m; i++){
	       	for(j = 0; j<=m; j++){
	  	      	minst[i][j] = 0;  
			    minst[j][i] = 0; 
			    minstdu[i] = 0;
			    minstdu[j] = 0;
			    Connected[i] = 0;
			    Connected[j] = 0;
			}
		}
	    mstcostnum = 0;
	}
    for(i = 2, minnum = sum[1]; i<=m; i++)
	{
		if(minnum>sum[i])
		{
			minnum = sum[i];
		}
	} 
	for(i = 1; i<=m; i++){
		if(minnum==sum[i])
		{
			printf("------分析------\n");
			printf("由顶点%d生成的最小生成树求得的路径距离值最小，为%d\n",i,sum[i]);
		}
	}
    return 0;  
}